基于神经网络的微生物生长预测模型

侯 奇HOU Qi

刘 静1

管 骁2

(1.上海海事大学信息工程学院，上海 201306；2.上海理工大学医疗器械与食品学院，上海 200093)

预测微生物学本质上是基于微生物群体对环境因素反应的可重现，利用过去观察到的试验数据通过数学模型预测食物环境中的微生物行为，并用试验结果证明模型所得到的误差不大于微生物试验所带来的误差[1]。由Whiting等[2]提出的基于变量类型的分类方法将预测微生物数学模型分为一级模型、二级模型和三级模型，其中二级模型描述微生物在食品中的生长情况与环境条件之间的关系，代表性模型包括反应面模型、平方根模型和多项式模型等，而现有的大多数二级模型对微生物生长的延滞期、指数期、稳定期和衰亡期并不能同时进行很好地预测。

Fujikawa[3]提出的数学模型中，以Baranyi模型为基础，通过环境各方面的响应函数作为Baranyi参数的二级模型，对指数期和稳定期能够很好地预测，但是对延滞期并不能进行有效地拟合。为了提高对延滞期的预测精度，Baranyi[4-5]和 Marc等[6]提出了多种延滞期的模型，但这些模型都太过针对性，对其他阶段不能起到良好的预测。Huang[7]提出滞后相变系数模型，它能够对各个时期有良好的过渡效果，但是只有滞后相变系数取值为25时，其模型才拟合得较好，因此缺少通用泛化性。然而，这些模型中的参数都是凭经验建立，其中很多参数没有实际意义，并且参数模型通常需要进行校准避免误差的不确定性[8-9]，因此很难确切地反映环境因数对生长预测的影响。

部分研究者[10]采用人工神经网络方法(artificial neural networks，ANN)进行建模，在存在不确定数据和测量误差的情况下，基于ANN的模型会比经验模型产生更准确的预测，如Xiao[11]、Kodogiannis[12]用ANN来拟合环境因数作为模型中的参数，但其模型实质还是半参数化的预测模型，并没有很好地利用ANN的优点。本研究拟提出一种基于BP&ELMAN神经网络的非经验化模型，以期解决经验型模型参数过多的问题和提高模型预测的准确性。

1 人工神经网络

1.1 BP神经网络

BP神经网络的特点是逐步将输出错误反向传播，解决了隐含层连接权学习问题。用于输入输出模型的大量映射关系，其学习规则采用最快下降法，以实现平方的最小误差和，使得它常用于复杂问题的建模[13]，已经在图像、视频及手写识别等领域中实现了其最先进的性能，并且可以充分逼近任意复杂的非线性关系[14]。

1.2 ELMAN 神经网络

ELMAN网络是局部反馈连接的递归神经网络，具有动态映射功能，并使系统具有适应时变特性的能力[15]，其隐藏层使用一个具有与典型微生物生长曲线相似形状的Sigmoid函数，这让神经网络不需要使用大量节点就可以获得相应微生物生长曲线[16]，关联层通过联接记忆上一个时刻的隐层状态连同当前时刻的网络输入一起作为隐层的输入，相当于状态反馈，便于作时间类预测。

2 基于神经网络的预测模型应用与分析

2.1 基于神经网络的预测模型

根据试验需求设计网络具有3个输入神经元(温度、pH和Aw)，5个隐藏神经元和2个输出神经元(生长速率和倍增时间)的模型，可使网络架构具有良好的表现。本研究使用的BP网络结构图见图1。梯度方法用于校正反向传播算法中的权重，阈值函数见式(1)：

(1)

式中：

xi——输入向量(x1,x2,x3)T，x1,x2,x3分别为温度、pH和Aw；

m——输入向量的个数；

wi——权系数；

θ——阈值；

y——输出集。

传递函数必须可微，采用Log-Sigmoid函数，其函数定义见式(2)：

(2)

式中：

x——输入值。

x的范围是包含整个实数域的，函数值在0～1，它在分类时比线性函数更为精确。

由于微生物生长预测是关于时间动态化的过程，ELMAN神经网络对历史状态数据具有敏感性，增加了网络处理动态信息的能力，达到动态建模的目的，能使预测值均匀地分布在实际值的两侧，适合实时系统辨识的动态递归，对序列问题及时间问题有着很好的预测效果，综合BP&ELMAN神经网络两者的优点，本研究提出新的预测模型：首先通过各个环境因素作为BP神经网络的输入，通过训练好的BP网络得到生长速率和倍增时间(表征微生物生长速率的一个参数)，其次，通过BP网络输出的结果与微生物的初始浓度作为ELMAN神经网络的输入，最终得到生长曲线。它能有效地避免人为计算的误差，最大精度地保障环境因素对其生长动力学的影响，其结构流程图见图2。

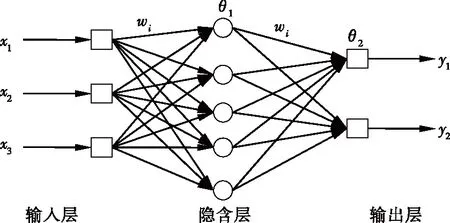
图1 BP神经网络结构图Figure 1 BP neural network structure

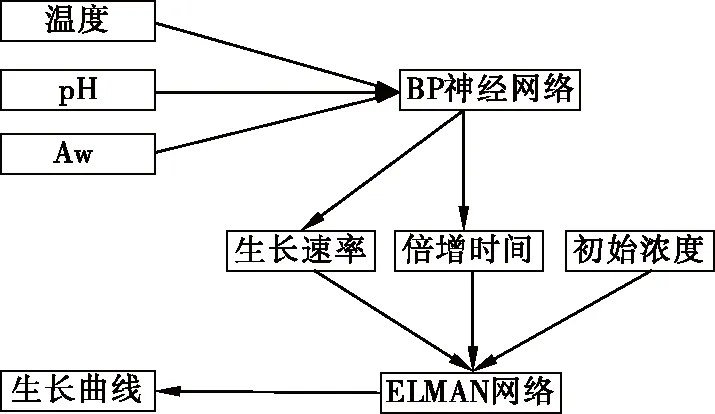
图2 基于神经网络的微生物预测模型Figure 2 Microbial prediction model based on neural network

2.2 样本数据的描述

本研究选取食品主要致病菌之一的李斯特菌为研究对象，已被证实肉类、蛋类、禽类、海产品、乳制品、蔬菜等都是李斯特菌的感染源[17-18]，能够检验预测模型，具有广泛的应用范围，并且本模型能够适合各种微生物的生长动力学预测，并不是单一的针对李斯特菌所提出的模型，也可以应用于沙氏门菌、大肠杆菌等[19]。本研究微生物生长的数据来源于Combase数据库，Combase数据库是2003年由英美两国将PMP、FM和Growth Predictor进行整合而成的数据库模型，拥有40 489个关于微生物生长和存活的数据，并且也是世界上最大的预测微生物学信息数据库。本研究选取的李斯特菌试验数据对象环境为温度1～40 ℃、pH值4.4～7.5、Aw 值0.934～1.000，试验数据共120组。

2.3 应用与分析

2.3.1 基于BP神经网络对生长速度拟合 通过随机选择100组试验数据集对BP网络进行训练，每次仿真随机抽取测试组数据20组，重复进行50次仿真以确保模型的稳定性。通过训练好的网络进行验证，将模型预测结果与实际数据进行对比，得测试数据与实际值的线性回归图见图3。由图3可知，其生长速率和倍增时间相关系数分别达0.998 6和0.998 3，具有良好的拟合效果。

2.3.2 基于ELMAN神经网络对生长浓度的预测 将BP网络拟合的生长速度与初始浓度和倍增时间作为ELMAN神经网络的输入，先通过100组实测数据对ELMAN神经网络进行模型训练，然后通过20组测试组数据对网络进行仿真测试，最后得到与时间相关的微生物一级生长曲线模型。使用李斯特菌在温度20 ℃，pH 7，Aw 0.997条件下的数据，对本研究预测模型与经典Baranyi模型进行预测，结果见图4(a)，与之对应的残差图见图5(a)；图4(b)是李斯特菌在温度19.7 ℃，pH 6.6，Aw 0.987条件下预测对比结果，与之对应的残差图见图5(b)；图4(c)是李斯特菌在温度20.5 ℃，pH 7.2，Aw 0.967条件下预测对比结果，与之对应的残差图见图5(c)；图4(d)是李斯特菌在温度20.3 ℃，pH 7，Aw 0.981条件下预测对比结果，与之对应的残差图见图5(d)。通过图4和图5可知，本模型预测结果更符合实际情况，误差相对于Baranyi模型要小，在生长期到稳定期的过渡阶段，预测的正确度尤其明显。

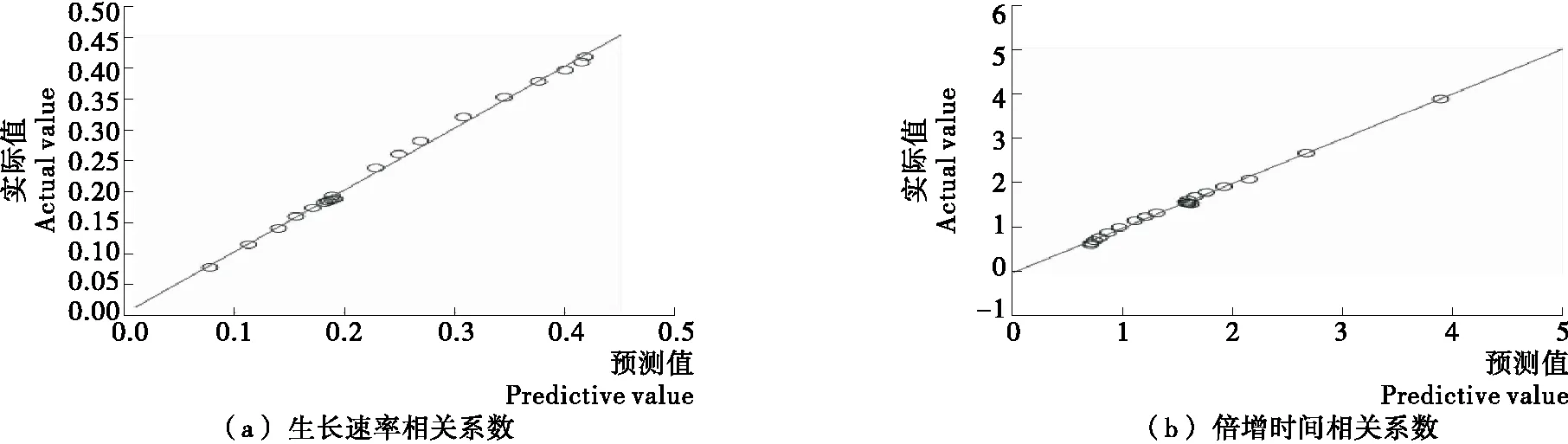
图3 生长速率和倍增时间的预测值与实际值的线性回归Figure 3 The linear regression of Growth rate and multiplication time of the predicted value and the actual value

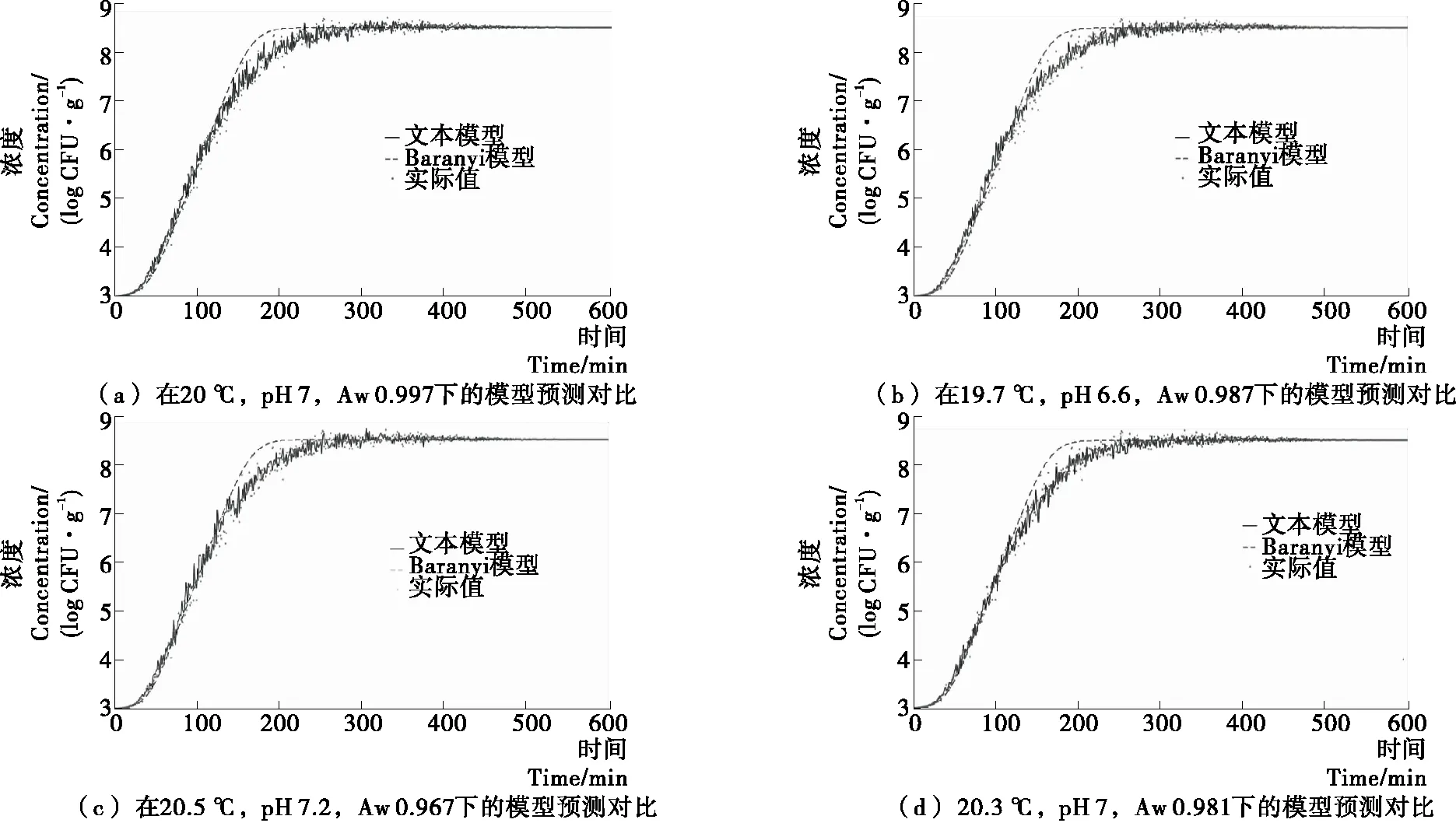
图4 本研究预测模型与Baranyi模型对比结果Figure 4 Shows the comparison between the model and the Baranyi model

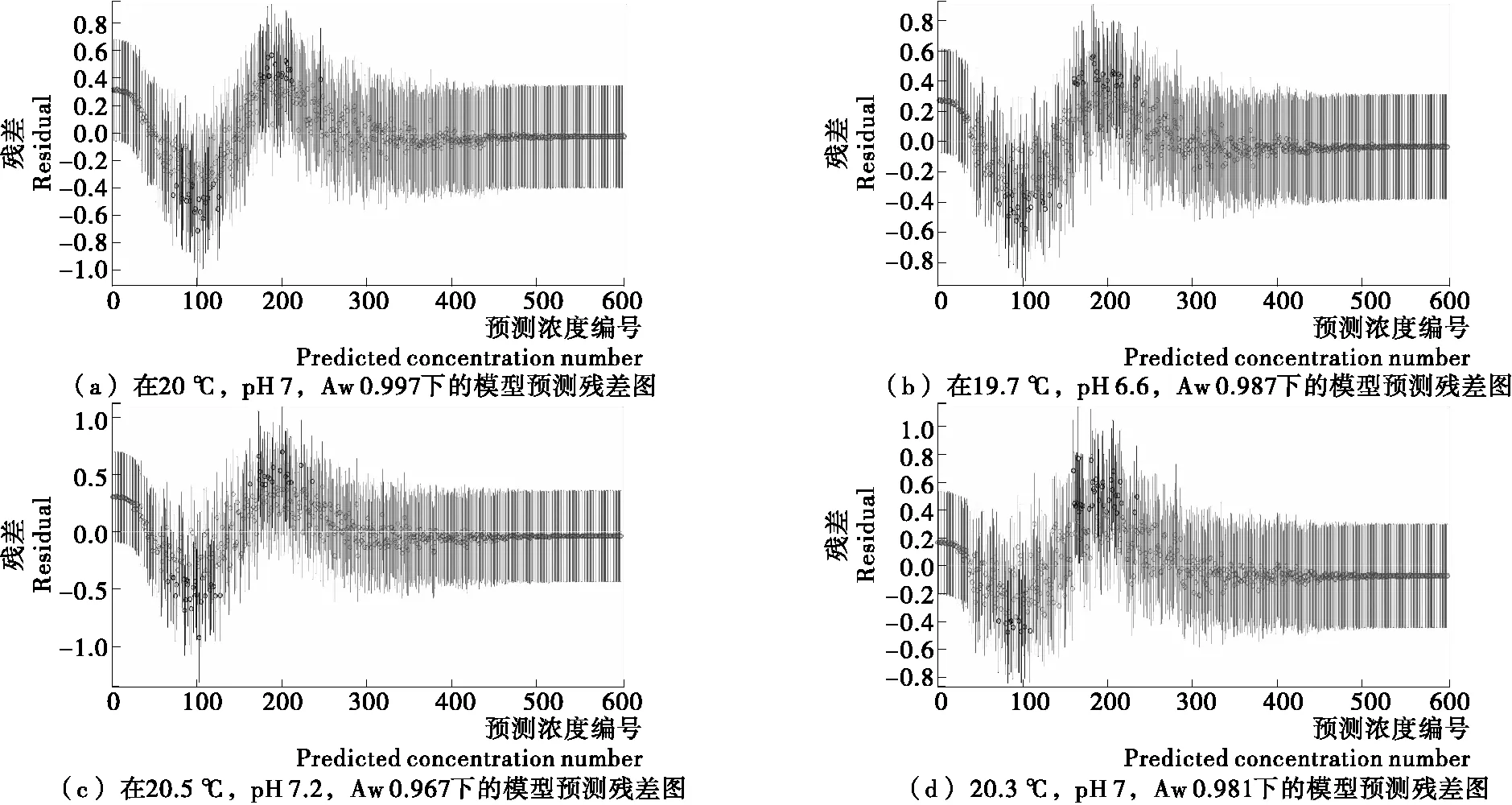
图5 残差图Figure 5 Residual plot

2.3.3 预测结果讨论 BP网络训练过程中没有过拟合的情况发生，网络输出集合的线性回归相关系数接近0.99，说明网络架构已达到预期期望。50次重复试验的预测输出结果显示，生长速率和倍增时间实测数据与预测数据的线性回归相关系数处于[0.932 1，0.998 4]和[0.962 0，0.998 3]之间，得到良好拟合效果。从ELMAN网络的预测结果可以看出，本研究模型对微生物生长的各个时期有很好的预测效果，并且从其残差分析的结果可知，异常点约占总体的5%，在可接受范围内。

3 结论

本研究选取李斯特菌为研究实例，利用其试验环境的温度、pH值和Aw 值建立BP神经网络二级生长模型，所得模型对微生物生长速度和倍增时间预测相关系数分别为[0.932 1，0.998 4]和[0.962 0，0.998 3]；再将所得到的生长速度和倍增时间结合初始浓度，建立ELMAN神经网络，从而得到与时间相关的微生物生长一级模型。通过与其他模型数据对比，本模型数据更偏向于实际环境下的预测结果，经残差分析结果可知，异常点约占总体的5%，试验结果显示，该模型可以对微生物生长的各个时期进行有效预测，并解决经验型模型参数化过多，以及没有生物意义的问题。由模型对比知，本模型在生长期到稳定期的预测有着更高的准确性。此外本模型能够预测微生物在更多的环境条件下的生长和灭活，由于不限制影响微生物生长因子的个数可大大提高本模型的通用性，可使得微生物预测模型能有较好的应用空间，可以帮助研究人员对微生物生长的动态进行分析，以及在复杂环境下对微生物生长失活进行预测。

[1] PEREZ-RODRIGUEZ F, VALERO A.Predictive microbiology in foods[M].New York: Springer-Verlag, 2012: 1-10.

[2] WHITING R C, BUCHANAN R L.Predictive food microbiolo-gy[J].Trends in Food Science and Technology, 1994, 4(1): 6-11.

[3] FUJIKAWA H.Application of the new logistic model to microbial growth prediction in food[J].Biocontrol Science, 2011, 16(2): 47-54.

[4] BARANYI J.Comparison of stochastic and deterministic conce-pts of bacterial lag[J].Journal of Theoretical Biology, 1998, 192(3): 403-408.

[5] BARANYI J.Stochastic modelling of bacterial lag phase[J].International Journal of Food Microbiology, 2002, 73(2/3): 203-206.

[6] MARE Le, ELFWING A, BARANYI A, et al.Modelling the variability of lag time and the first generation times of single cells ofE.coli[J].International Journal of Food Microbiology, 2005, 100(1): 13-19.

[7] HUANG Li-han.Optimization of a new mathematical model for bacterial growth[J].Food Control, 2013, 32(1): 283-288.

[8] BALSAC E, ALONSOLONSO A A, BANAGA J R.An iterative identi-fication procedure for dynamic modeling of biochemical networks[J].BioMed Central, 2010, 4(1): 33-46.

[9] FILIPL, BORIS H, MORITZ D.Robust multilobjective optimal control of uncertain (bio)chemical processes[J].Chemical Engineering Science, 2011, 66(20): 4 670-4 682.

[10] GARCIA-GIMENO R M, HERVAS-MARTINEZ C, SILONIZ M, et al.Improving artificial neural networks with a pruning methodology and genetic algorithms for their application in microbial growth prediction in food[J].Food Microbiol, 2002, 72(1/2): 19-30.

[11] XIAO Hai-tao, LI Bai-lin, OU Jie.Predicting the bacterial growth in MAP chilled beef by artificial neural networks[J].Journal of Pure & Applied Microbiology, 2013, 7: 123-129.

[12] KODOGIANNIS V S, PACHIDIS T, KONTOGIANNI E.An intelligent based decision support system for the detection of meat spoilage[J].Engineering Applications of Artificial Intelligence, 2014, 34(3): 23-36.

[13] BASHEER I, HAJMEER M.Artificial neural networks: fundamentals, computing, design, and application[J].Journal of Microbiological Methods, 2000, 43(1): 3-31.

[14] 王学武, 谭得健.神经网络的应用与发展趋势[J].计算机工程与应用, 2003, 39(3): 98-100.

[15] LIU Hui, TIAN Hong-qi, LIANG Xi-feng.Wind speed forecasting approach using secondary decomposition algorithm and Elman neural networks[J].Appl.Energy, 2015, 157: 183-194.

[16] PALAEIOS A P, MARIN J M, QUINTO E J, et al.Bayesian modeling of bacterial growth for multiple populations[J].The Annals of Application Statistics, 2014, 8(3): 1 516-1 537.

[17] OHKOCHI M, KOSEKI S, KUNOU M, et al.Growth modeling of Listeria monocytogenes in pasteurized liquid egg[J].J Food Prot, 2013, 76(9): 1 549-1 556.

[18] MEJLHOLM O, GUNVIG A, BORGGAARD C, et al.Predicting growth rates and growth boundary of Listeria monocytogenes-an international validation study with focus on processed and ready-to-eat meat and seafood[J].International Journal of Food Microbiology, 2010, 141(3): 137-150.

[19] ZHOU Kang, ZHONG Kai-cheng, LONG Chao, et al.Development and validation of a predictive model for the growth of salmonella enterica in chicken meat[J].Journal of Food Safety, 2014, 34(4): 326-332.