真空环境下小孔节流式静压气体轴承流场特性与轴承性能分析

李运堂 王 军 万 欣 吴进田 李孝禄

中国计量大学机电工程学院，杭州，310018

0 引言

气体轴承是未来微电子制造及其测量装备最主要的运动支撑元件。真空下气体轴承出口附近气体稀薄，轴承内黏性流、过渡流、分子流共存。由于Navier-Stokes方程仅适用于黏性流，不能分析更为复杂的过渡流和分子流，因此，一些学者在Navier-Stokes方程基础上利用滑移模型修正润滑方程，用于分析真空下静压气体轴承的性能。BURGDORFER[1]利用一阶速度滑移边界分析气体稀薄效应对气体润滑的影响。张海军等[2]认为随着气体稀薄程度增大，轴承承载能力下降，稀薄效应随轴承数减小而降低。陈东菊等[3]研究了稀薄效应下流量因子对气体轴承性能的影响。傅仙罗[4]指出真空下静压气体轴承更易发生自激振动。针对过渡流和分子流的分析计算，FRUKUI等[5-6]研究了表面节流气体轴承在10-3Pa环境下的气压分布，基于Boltzmann方程提出适用于过渡流和分子流的广义润滑方程，根据黏性流所占比例，提出可缩短计算时间的迭代方法，并用实验验证了润滑方程的有效性。TROST[7]以单回流槽静压气体轴承为对象，假设流动状态由黏性流直接转变为分子流，推导出流动状态转变位置和转变压力。SCHENK等[8]以圆盘形小孔节流气体轴承为研究对象，提出任意供气压力下气体轴承性能计算解析模型，其仿真计算和实验结果表明，真空下轴承承载能力增大、刚度减小，最佳气膜厚度增大。在润滑气体回收和轴承密封方面，KHIM等[9]认为轴承运动、加/减速时轴承倾斜、导轨表面对气体分子吸附作用等因素引起润滑气体泄漏，导致真空室压力升高。并进一步用实验分析证明[10-12]：运动速度造成的泄漏量最大，加/减速因时间短所产生的影响可忽略不计，在导轨表面增加氮化钛等低气体分子吸附涂层可以减小润滑气体泄漏，然后采用遗传算法优化排气系统，指出影响真空压力的主要因素为排气系统数量、排气管直径、长度及气膜厚度等。

本文采用文献[7]的研究思路，忽略真空环境下静压气体轴承流场内的过渡流，计算黏性流向分子流转变的临界半径和临界压力，获得轴承内气体压力分布，纠正了文献[7]错误的计算式和分析结果。在此基础上，分析了轴承内气体流场特性和轴承。

1 真空环境下静压气体轴承结构

真空环境下圆盘形简单孔式节流静压气体轴承结构如图1所示。压缩机产生的高压润滑气体经节流孔后高速喷入气腔，继续流动过程中在轴承与止推面之间的微小间隙内形成具有一定压力的气膜，从而起到运动支承作用。为避免润滑气体污染真空环境，设置了由排气槽、密封间隙和真空泵组成的密封单元，根据真空室压力和润滑气体泄漏量要求确定密封单元数量、各级真空泵抽速和极限压力，形成密封系统。密封系统必须确保绝大部分润滑气体排入外部环境，极少量自轴承外缘泄漏的润滑气体被与真空室相连的真空泵及时抽走，以维持真空压力和洁净度，首个排气槽可与真空泵或真空室外部连接。图1中，d1为节流孔直径，R、r2和rs1分别为轴承半径、气腔半径和首个排气槽半径，w1、w2为回流槽宽度，l1、l2为密封间隙长度，h为气膜厚度。

图1 真空环境下静压气体轴承结构Fig.1 Structure of aerostatic thrust bearing with pocketed-orifice type restrictor working in vacuum condition

2 真空环境下静压气体轴承流场计算

通常情况下，静压气体轴承供气压力p1∈0.3～0.5 MPa，真空室压力pe∈10-1～10-6Pa。润滑气体在气膜内流动时，气流通道面积逐渐增大，压力和密度逐渐减小，气体分子平均自由行程增大，稀薄效应越来越显著。因此，轴承内黏性流、过渡流和分子流共存。为计算方便，忽略过渡流，将流场分为黏性流动区域和分子流动区域两个区域，如图2所示。其中，rsn为第n个排气槽内径，rt为黏性流向分子流转变位置(临界半径)。单个密封单元的密封系统，rt位于r2与rs1之间；多个密封单元的密封系统，rt位于r2和rsk之间，k=1, 2, …,n。

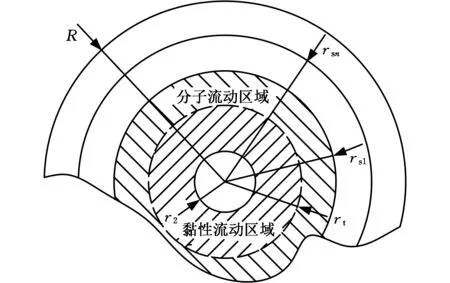
图2 黏性流-分子流计算模型Fig.2 Viscous-molecular calculation model

不失一般性，假设黏性流向分子流转变位置发生在气腔与首个排气槽之间，则r2～rt区域内：

(1)

式中，Q为单位时间流场内任意一点压力和体积的乘积；μ为气体黏性系数；p2为气腔压力；pt为黏性流向分子流转变压力(临界压力)。

在rt～rs1区域内：

(2)

式(2)是基于气体流过宽度为2πrs1的矩形截面槽得出的，因此，rt/rs1→1。利用式(1)和式(2)消去Q得

(3)

(4)

由于Φ≪1,式(1)和式(2)分别对rt求导得

(5)

(6)

式(5)、式(6)分别为黏性流和分子流区域的临界压力pt对临界半径rt的求导，由式(5)和式(6)可知，在黏性流动区域，∂pt/∂rt与pt成反比，而在分子流区域，∂pt/∂rt与pt无关。忽略过渡流，令式(5)和式(6)相等，可确定黏性流向分子流转变临界压力：

(7)

黏性流-分子流转折曲线如图3所示。

图3 黏性流-分子流转折Fig.3 Viscous flow transition to molecular flow

将式(7)代入式(3)得

(8)

由气体黏性系数

平均气体流速

可得

(9)

式中，玻尔兹曼常数k=1.38×10-23J/K;T为环境温度(K);m为气体分子质量。

取rs1为特征值对几何参数进行量纲一化，得

设气流通道参数s=rs1/h，可得

(10)

(11)

量纲一化后，式(8)写成

(12)

黏性流动和分子流动区域量纲一气体压力分布可分别采用下式计算：

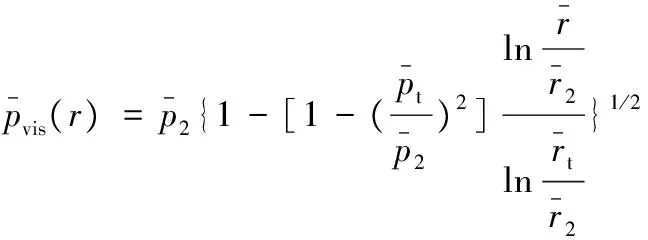
(13)

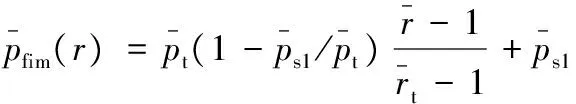
(14)

对轴承上下表面所受压力差的面积积分获得承载能力

(15)

式(6)～式(8)、式(10)、式(12)～式(14)在文献[7]中对应的公式分别如下：

3 设计参数和润滑气体对流场和轴承性能的影响

图4给出了气流通道参数s与临界半径和临界压力之间的关系。s确定后，临界压力随临界半径增大而减小，其原因在于：临界半径靠近排气槽，随着气流通道面积增大，气体稀薄程度越显著，分子平均自由程越大。由于气体压力与分子平均自由程成反比，因此临界半径越大，临界压力越小。图4还表明，临界压力随s增大而增大，其原因在于：轴承耗气量在黏性流区域与气膜厚度三次方成正比，分子流区域与气膜厚度二次方成正比，而气流通道面积与气膜厚度成正比。s增大等同于气流通道面积减小，导致轴承耗气量减小，当回流槽气体压力不变且为分子流时，黏性流向分子流转变的临界半径减小，从而气流通道面积减小，使临界半径远离回流槽，临界压力增大。

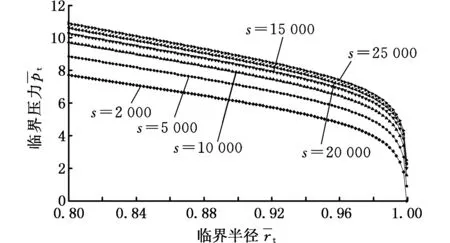
图4 s与临界半径和临界压力之间的关系Fig.4 Influence of s on critical radius and critical pressure

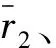
图5 气腔半径、气腔压力与临界半径之间的关系Fig.5 Influence of air chamber radius, pressure on critical radius

图6 不同临界半径在承载区轴承径向压力分布Fig.6 Pressure distribution in radius with different critical radius

图7 特征压力与润滑气体和环境温度之间关系Fig.7 Relationship between characteristic pressure and lubricant gas and temperature

基于微电子制造工艺需求，当空气作为润滑气体不能满足要求时，需要采用其他气体作为润滑介质，因此，轴承性能不仅受润滑气体的特征压力、分子直径和质量的影响，还与环境温度直接相关。图7所示为氮气(N2)、二氧化碳(CO2)、氩气(Ar)和氦气(He)在不同温度时的特征压力。在相同温度下，由于He分子直径最小，特征压力最大，而N2分子直径最大，特征压力最小，CO2和Ar的特征压力居中。

作为简单孔式节流静压气体轴承的关键几何参数，气腔半径取值应在合理范围内，半径过大将影响节流孔的节流效应，降低轴承刚度，半径过小均压作用不明显，承载能力降低。通常情况下，气体轴承的供气压力为0.3～0.5 MPa，不同润滑气体在不同温度下的特征压力限制量纲一气腔压力，如图8所示，受不同气体特征压力影响，N2的特征压力的取值范围最大，适当增大轴承直径，可获得较高的承载能力，He的特征压力取值范围最小，增大轴承半径只能导致临界半径远离排气槽而无法明显提高承载能力，CO2和Ar的特征压力取值范围居中，使用时应该综合考虑。在0～100 ℃内，N2、CO2和Ar量纲一气腔压力有较大的重叠区域(图中深色区域)，在0 ℃时重合区域量纲一气腔压力为87～119，100 ℃时重合区域无量气腔压力为56.5～89，由前文分析可知，量纲一气腔压力与气腔直径密切相关，根据气腔压力可确定气腔大小。

图8 气腔压力与环境温度之间的关系Fig.8 Relationship between lubricant gas and environmental temperature

4 结语

本文采用文献[7]的研究思路，忽略真空环境下静压气体轴承内流场的过渡流，假设黏性流直接转变为分子流，根据流场参数约束关系得出了黏性流转变为分子流的临界半径和临界压力，纠正了文献[7]中部分计算公式的错误，同时将文献[7]中黏性流动区域∂pt/∂rt与pt的线性关系纠正为本文图3的非线性关系。

在此基础上，研究了气流通道、气腔半径、气腔压力对临界半径和临界压力的影响，并分析了产生相关现象的原因。同时，研究了温度对润滑气体特征压力的影响并给出了相应的气腔压力的合理取值范围。结果表明：当气流通道参数确定后，临界压力随临界半径的增大而减小；临界压力随气流通道面积增大而增大；增加气腔压力和气腔直径，临界半径显著增大；在相同温度下，N2的特征压力最大，He的特征压力最小，CO2和Ar的特征压力居中；在供气压力为0.3～0.5 MPa时，He为润滑介质可获得较高的承载能力，He作为润滑介质承载能力偏低，但结构小巧，应用时应综合考虑。

参考文献：

[1] BURGDORFER A. The Influence of the Molecular Mean Free Path on the Performance of Hydrodynamic Gas Lubrication Bearings[J]. ASME Journal of Basic Engineering,1958,81(1):94-100.

[2] 张海军, 祝长生, 杨琴. 基于稀薄效应的微气体径向轴承稳态性能[J]. 力学学报,2005,41(6):941-946.

ZHANG Haijun, ZHU Changsheng, YANG Qin. Steady Characteristics of Micro Gas Journal Bearings Based on Rarefaction Effect[J]. Chinese Journal of Theoretical and Applied Mechanics,2005,41(6):941-946.

[3] 陈东菊. 稀薄效应对空气静压止推轴承性能影响[J]. 四川大学学报(工程学科版),2016,48(1):194-199.

CHEN Dongju. Influence of Flow Factor in Gas Rarefied Effects to Aerostatic Thrust Bearing[J]. Journal of Sichuan University (Engineering Science Edition),2016,48(1):194-199.

[4] 傅仙罗. 静压气浮轴承在真空中的自振问题[J]. 航空学报,1981,2(4):70-78.

FU Luoxian. Self-excited Resonance of Aerostatic Bearing Working in Vacuum Environment[J]. Acta Aeronautica et Astronautica Sinica,1981,2(4):70-78.

[5] FUKUI S, KANEKO R. Analysis of Ultra-thin Gas Film Lubrication Based on Linearized Boltzmann Equation: First Report-derivation of a Generalized Lubrication Equation Including Thermal Creep Flow[J]. Transaction of ASME, Journal of Tribology,1988,110:253-261.

[6] FUKUI S, KANEKO R. Experimental Investigation of Externally Pressurized Bearings under High Knudsen Number Conditions[J]. Transaction of ASME, Journal of Tribology,1988,110:144-147.

[7] TROST D. Design and Analysis of Hydrostatic Gas Bearings for Vacuum Applications[C]// Proceedings of ASPE Spring Topical Meeting on Challenges at the Intersection of Precision Engineering and Vacuum Technology.Seattle,2006:54-59.

[8] SCHENK C, BUSCHMANN S, RISSE S, et al. Comparison between Flat Aerostatic Gas-bearing Pads with Orifice and Porous Feedings at High-vacuum Conditions[J]. Precision Engineering,2008,32(4):319-328.

[9] KHIM G, PARK C H, LEE H, et al. Analysis of Additional Leakage Resulting from the Feeding Motion of a Vacuum-compatible Air Bearing Stage[J]. Vacuum,2006,81(4):466-474.

[10] KHIM G, PARK C H, LEE H, et al. Optimal Design of an Exhaust System of a Vacuum-compatible Air Bearing[J]. Journal of the Korean Society for Precision Engineering,2007,24(6):86-95.

[11] KHIM G, PARK C H, LEE H, et al. Performance Analysis of a Vacuum-compatible Air Bearing[J]. Journal of the Korean Society for Precision Engineering,2006,23(10):103-112.

[12] KHIM Y, PARK C H. A Rotary Stage in a Vacuum Using an Air Bearing[J]. Vacuum,2014,105:39-45.