武陵山区域旅游景区系统空间结构的分形研究

余茭茭，易正萍，万亚男，涂 敏，毛 志*

（ 铜仁学院 大数据学院，贵州 铜仁 554300）

0．引言

随着我国旅游业的快速发展、基础设施的不断改善和区域经济一体化进程的加快，许多非中心旅游地区旅游业实现了跨越发展并带动所在区域的经济发展，该领域的研究受到政府部门和学术界的广泛关注。旅游空间结构优化是目前促进旅游地区旅游资源开发与发展的难点。[1]国内外学者采用聚类分析[2]、SSM（转移—份额分析法）[3]等方法，从多个角度对旅游空间结构进行研究。分形理论由美国科学家B.B.Mandelbrot于20世纪70年代中期创立，主要研究和揭示复杂的自然现象和社会现象中所隐藏的规律性、层次性和标度不变性，为人们通过部分认识整体，从有限认识无限提供了一种新的工具[4]。20世纪80年代，在旅游景区系统空间结构领域的研究中引入了分形理论及其方法。B.T.Milne首先采用分形理论对旅游景观空间结构进行了研究[5]。此后，分形理论和方法被广泛运用于旅游景观分形特征、景观形成机制、城市旅游景区系统空间结构的分形特征及优化对策等方面的研究[6-9]。但是，还少有学者运用分形理论来研究区域旅游景区系统的空间结构。同时，运用分形理论在旅游领域的研究多集中在旅游热点城市和中心地域，而应用于旅游资源丰富、旅游特色明显的非中心旅游地区旅游业研究极少。

武陵山区域跨湖北、湖南、重庆、贵州四省市，集革命老区、民族地区和贫困地区于一体，是跨省交界面大、少数民族聚集多、贫困人口分布广的连片特困地区，也是重要的经济协作区。区域内旅游资源丰富，自然景观独特，组合优良，极具开发潜力。国务院已批复的《武陵山片区区域发展与扶贫攻坚规划（2011—2020年）》明确提出将该区域建设成国际知名生态文化旅游区和长江流域重要生态安全屏障。因此，本文基于分形理论，通过测算分形维数，分析武陵山区域旅游景区系统的空间结构特征，既拓展了分形理论在区域旅游景区系统空间结构中的研究，又为武陵山区域旅游发展、区域旅游空间结构优化提供参考依据。

1．研究方法与数据来源

1．1．研究方法

分形维数是描述自然界和非线性系统中不光滑和不规则几何体的有效工具，是所有分形对象的主要特征之一和反映空间现象的重要参数。本文选取聚集维数和关联维数分析旅游景区系统的空间分形结构。

1．1．1．聚集维数

区域旅游景区系统某种程度上按自相似规律围绕中心旅游景区成凝聚态分布，并且假定区域旅游景区系统分形体是各向均匀变化的，则在半径为R的圆周空间范围内的旅游景区数目 N（ R）与半径R之间满足如下关系：

其中D为分形维数值，反映区域内景区围绕中心景区随机聚集的特征，故称之为聚集维数。考虑到半径R的取值会影响聚集维数的值，因此将其转化为平均半径：

其中Ri为第i个旅游景区到区域中心旅游景区的欧氏距离，N为区域旅游景区的个数。有如下分维关系：

转化为对数线性形式可得：

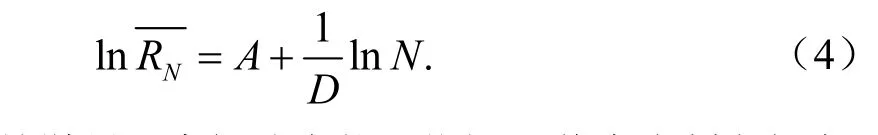
区域旅游景区空间分布状况依据D值大小判定如表1。

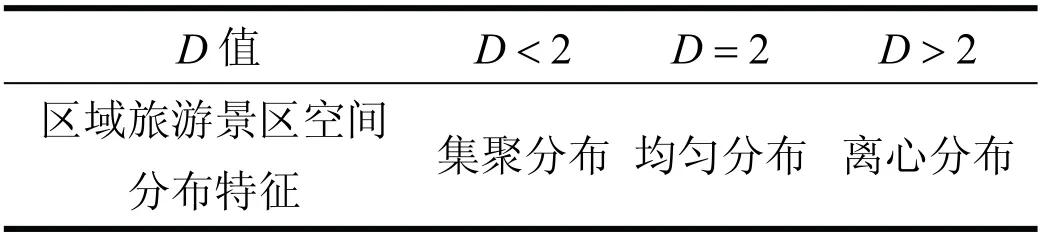
表1 聚集维数与区域旅游景区空间分布特征的关系

1．1．2．关联维数

空间上彼此分离的景区之间的相互作用是客观存在的。用分形理论中的点一点关联维数模型可以很好地模拟这种相互作用，其基本模型如下：

其中N表示区域内旅游景区数目，r为码尺，dij为i、 j两景区间的欧氏距离即乌鸦距离，θ为Heaviside函数，其具有如下性质：

显然，（4）式表示在以景区i为中心的半径r范围内出现景区j的概率。根据城镇空间分布的分形特征有：

转化为对数线性形式可得：

其中B为常量， D*为关联维数。关联维数反映了景区之间空间相互作用的规律性，取值范围一般介于0～2，其值越小，说明区域景区空间分布的集中度越高，空间联系越紧密，空间相互作用也越强；反之，亦然。

1．2．数据来源

选定七个武陵区域区旅游景区的数据进行分析，分别为：贵州铜仁梵净山景区、湖南张家界国家森林公园、湖南凤凰古城、湖南新宁崀山风景名胜区、湖北恩施大峡谷、重庆武隆天坑景区、重庆乌江大峡谷。在上述景区中一一选取代表性强、质量等级高的单个景点作为研究对象。本文根据武陵山区域旅游资源普查图及各景区地理位置图，采用人工判定法判定景区系统的无标度区间，在矢量图上标注出这七个景点。

2．结果与分析

2．1．武陵山区域景区结构的聚集维数测算

以铜仁梵净山为测算中心，首先运用ArcGIS10.0空间分析工具测量各景点到该中心的欧氏距离Ri，将其按有小到大顺序排列，通过改变N的值测算出一系列值，再把绘成双对数直线拟合图，通过最小二乘法求出聚集维数D的值。结果如表2和图1所示。所得到的聚集维数拟合模型为

总体拟合效果较好。武陵山区域景区系统的聚集维数值 D≈ 1.004 ＜ 2，表明武陵山区域旅游景区系统的空间结构随机聚集性较强，系统的演化尚处于有限扩散集团凝聚模型演化的中间阶段，中心景点的吸附作用比较强，但吸附半径不大，系统演变可能存在多中心并存的格局。

2．2．武陵山区域景区结构的关联维数测算

根据上述空间关联维数的测算模型，测算7个景点之间的欧式距离，构成乌鸦矩阵，取步长r=70，得到一系列（ r, C（ r ）） 的值，取双对数后进行线性拟合。结果如表3和图2所示。对无标度区内的散点进行线性回归，得关联维数拟合模型为

由此得出关联维数 D*= 1.1044，说明景点分布集中，几乎是均匀地分布在光滑曲线上，有利于形成环形旅游线路。

表2 以梵净山为中心的武陵山区域旅游景区系统聚集维数测算表

表3 武陵山区域旅游景区系统关联维数测算表

图1 景区系统聚集维数直线拟合图

图2 景区系统关联维数直线拟合图

3．结论

从以上分析可以看出，通过两种分形维数的测算，武陵山区域景区系统的空间结构具有分形特征，景区系统空间结构演化呈现自组织优化的趋势。武陵山区域景区系统在未来的演变过程中，会形成多中心并存的空间分布格局。

参考文献：

[1]崔大树，孙杨．基于分形维数的湖州旅游景区系统空间结构优化研究[J]．地理科学，2011，22（3）：337-343．

[2]王晓龙，刘笑明，李同升．主成分分析法、聚类分析法在旅游观光农业空间分区中的应用——以西安市为例的研究[J]． 数理统计与管理，2005，25（4）：6-13．

[3]汪宇明，高元衡．上海与长江流域各省区间的旅游互动[J]．地理学报，2008，63（6）：657-668．

[4]法尔科内．分形几何[M]．北京：人民邮电出版社，2007．

[5]Milne B T.Measuring the fractal geometry of landscapes[J].Applied Mathematics and Computation,1988,27(1):67-79.

[6]Bolviken B,Stokke P R,Feder J.The fractal nature of geochemical landscapes [J].Journal of Geochemical Exploration,1992,43(2):91-109.

[7]THOMAS I,Frankhauser P,Biernacki C.The morphology of built up landscapes in Wallonia(Belgium):A classification using fractal indices[J].Landscape and Urban Planning,2008,84(2):99-115.

[8]戴学军，丁登山，许志晖，等．旅游景区（点）系统空间结构随机聚集分形研究——以南京市旅游景区(点)系统为例[J]．自然资源学报，2005，20（5）：706-713．

[9]崔大树，孙杨．基于分形维数的湖州旅游景区系统空间结构优化研究[J]．地理科学，2011，31（3）：337-343．