一类具有Beddington-DeAngelis功能性反应的时滞捕食系统
2018-05-03魏苏林谢伟杰涂登琴张子振
魏苏林,沈 月,谢伟杰,涂登琴,张子振
( 安徽财经大学 管理科学与工程学院,安徽 蚌埠 233030)
0.引言
时滞在种群动力学中是一种普遍存在的现象。近年来,很多国内外学者对时滞种群动力系统稳定性[1-3]、持久性[4]、以及周期混沌现象[5-7]进行了大量研究。种群动力系统的动力学行为在很大程度上取决于系统中功能性反应函数。Beddington[8]和DeAngelis等人[9]提出Beddington-DeAngelis类功能性反应函数,此类功能性反应函数考虑到了捕食者种群内部之间的相互干扰,表现出了更加复杂的动力学行为。因此,具有Beddington-DeAngelis类功能性反应的时滞捕食系统模型的研究受到广泛关注。文献[10]提出并研究了如下同时具有Beddington-DeAngelis类和修正的Leslie-Gower类功能性反应的时滞捕食系统:
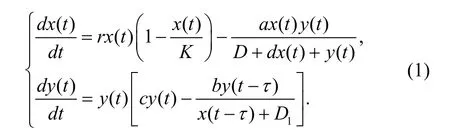
其中,x( t)和y( t)分别表示食饵种群和捕食者种群在时刻t的数量。r表示食饵种群的内禀增长率,K表示食饵种群的环境容纳量;a表示捕食者种群对食饵种群的捕食能力系数;D和d表示环境对食饵种群的保护能力系数;c表示捕食者种群的增长率;b表示捕食者种群的最大平均死亡率;D1表示由于所偏爱食饵的缺乏而导致捕食者种群数量的减少率;τ表示捕食者种群的妊娠时滞。文献[10]研究了时滞τ对系统(1)稳定性的影响。受文献[10]启发,并考虑到食饵种群的消极负反馈时滞,本文研究具有消极负反馈的时滞捕食系统:
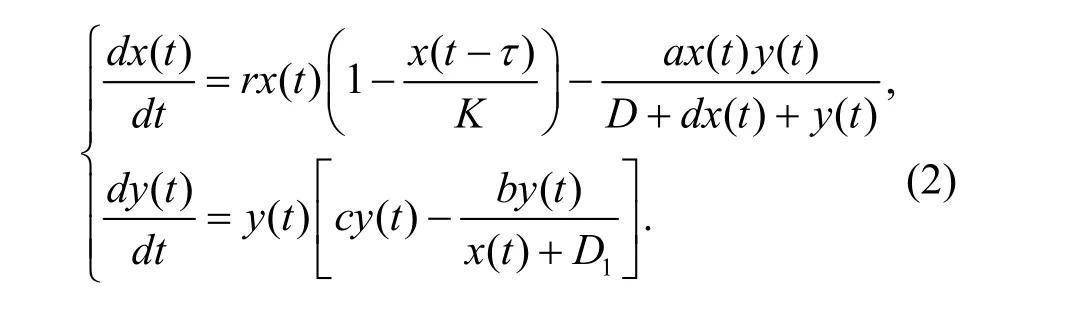
其中τ表示食饵种群的消极负反馈时滞。下面研究食饵种群的消极负反馈时滞τ对系统(2)稳定性的影响。
1.Hopf分岔的存在性
根据文献[10]的分析可知,如果 b>cD1,a>r并

如果系统(2)的系数给定,则可以利用Matlab软件求解出方程(7)的所有根。因此,为了给出本文主要结果,我们给出下列假设
(H1):方程(7)至少存在一个正根。
若条件(H1)满足,则存在ω0>0使得方程(4)具有一对纯虚根±ω0。对于ω0,根据方程(6)可以得到
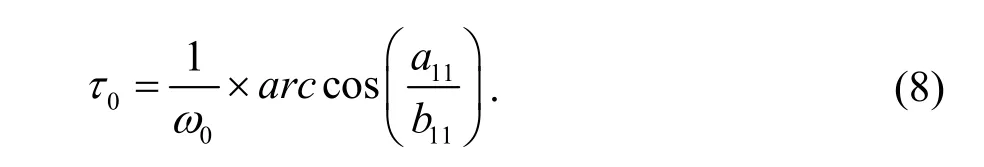
对方程(4)左右两边同时求λ关于τ的导数,有
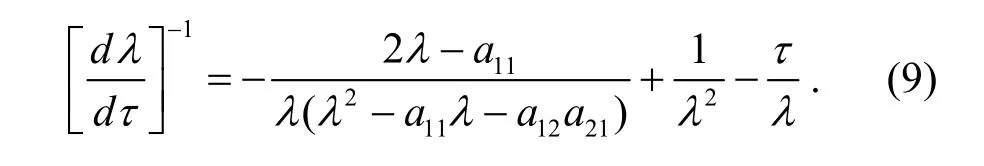
因此,
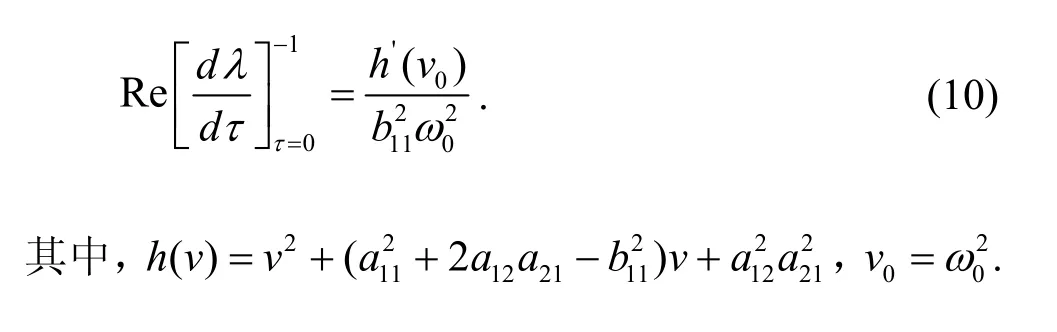
根据文献[11]中的结论,如果 h'( v0) ≠ 0,则系统(2)产生Hopf分支的横截性条件成立。于是,由[11]中的Hopf分支存在性定理可得下列结论。

2.仿真示例
为了验证以上所得理论结果的正确性,我们选取文献[10]中相同的参数:r=1,K=100,a=1,D= 1,d=0.01,c=0.01,b=0.2,D1=10.给出下列仿真示例:
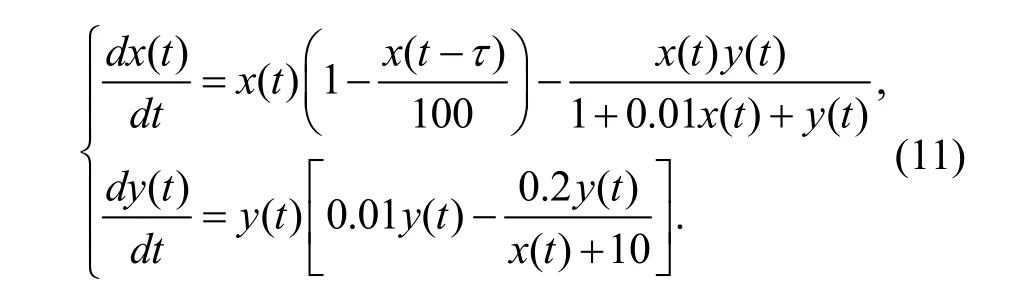
借助于Matlab软件,经过直接计算得到示例系统(11)的 唯 一 正 平 衡 点 E*(10,9.9).进 而 得 到ω0= 1.2081,τ0= 10.0517.根据本文所得理论结果可知,当食饵种群的消极负反馈时滞τ∈ (0,τ0= 10.0517)时,示例系统(11)的唯一正平衡点E*(10,9.9)是局部渐近稳定的。仿真效果如图1-2所示。一旦食饵种群的消极负反馈时滞τ的取值超越时滞临界点τ0= 10.0517,那么正平衡点 E*(10,9.9)将失去稳定性,并在τ0= 10.0517附近产生局部Hopf分支和一簇分支周期解。仿真效果如图3-4所示。
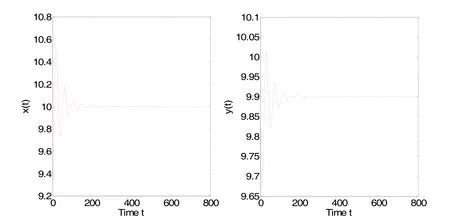
图1 τ=8.65< τ0时, E* (10,9.9)局部渐近稳定
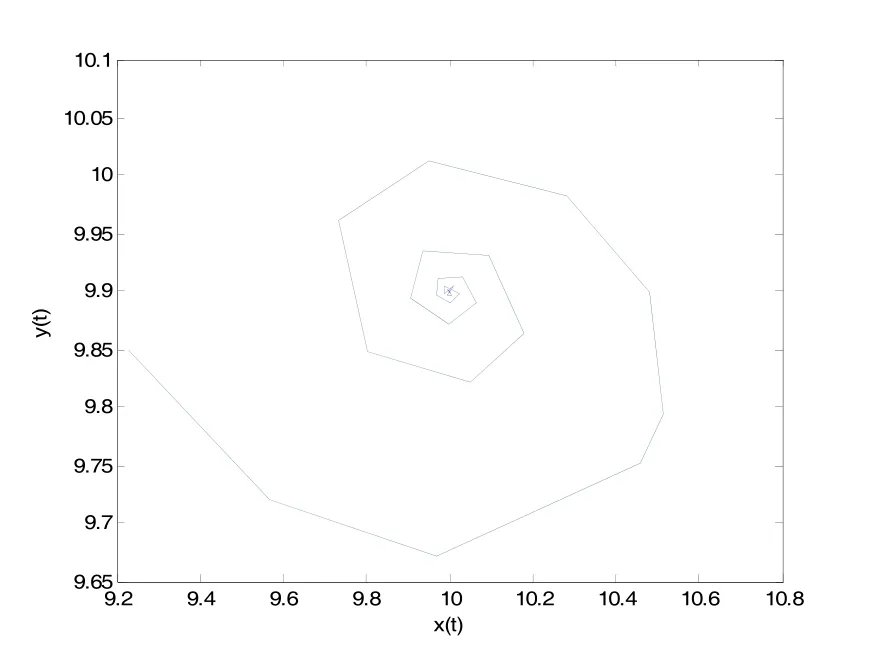
图2 τ=8.65< τ0时, x( t) -y( t)相图
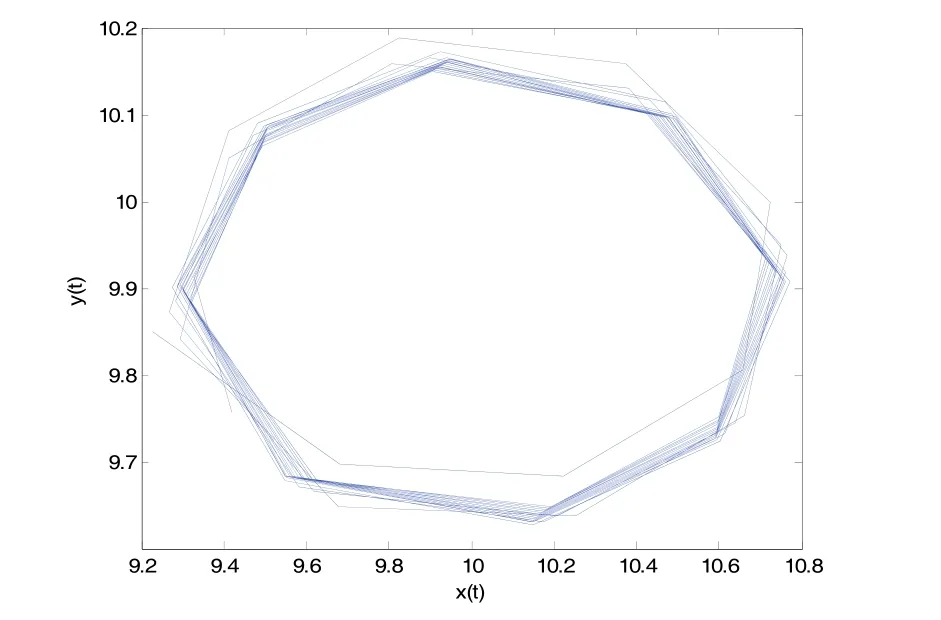
图3 τ=11.21> τ0时, x( t) -y( t)相图
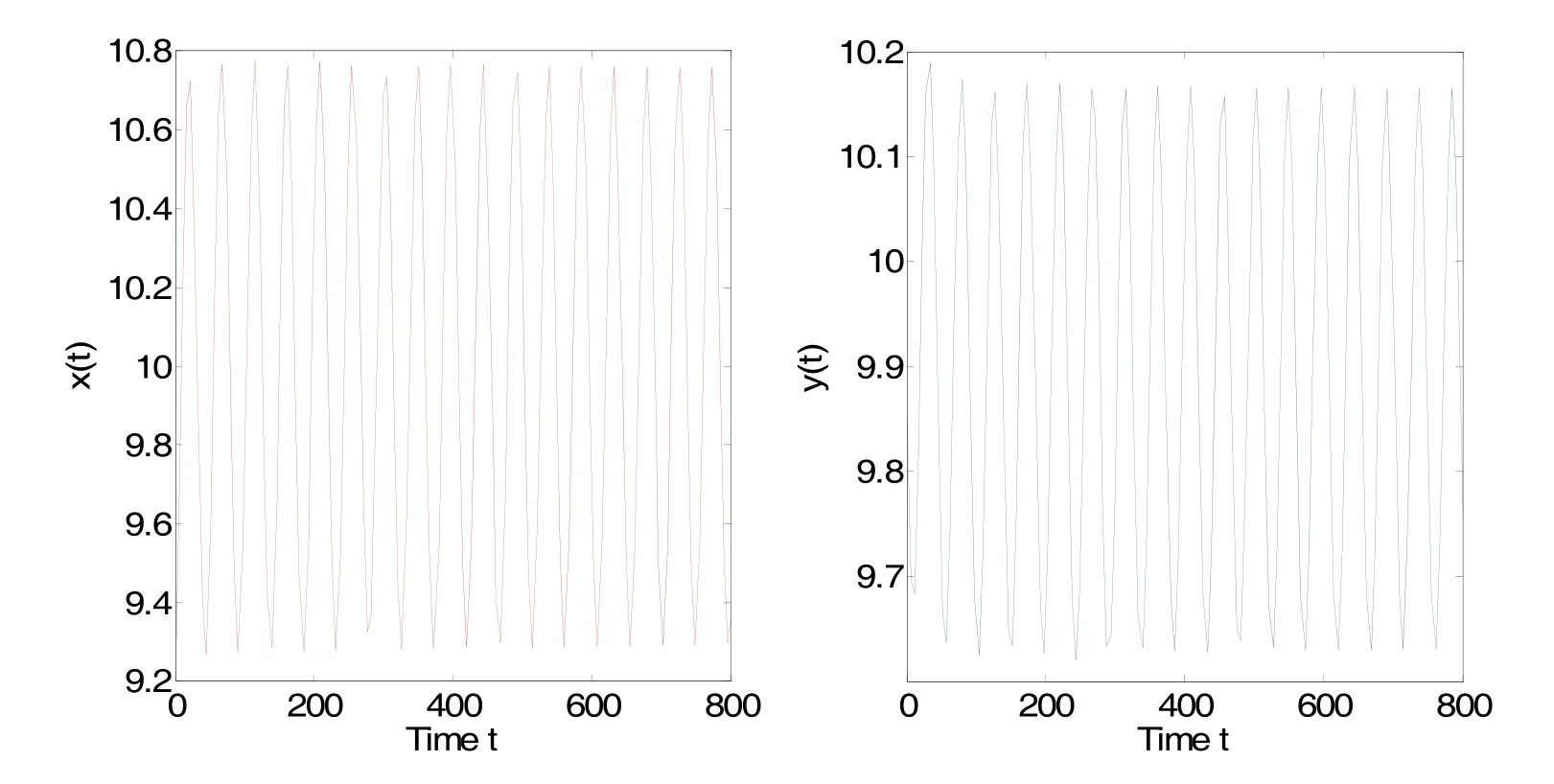
图4 τ=11.21>τ0,E* (10,9.9)失去稳定并产生Hopf分支
3.小结
本文在文献[10]的工作启发下,提出了一类同时具有Beddington-DeAngelis类和修正的Leslie-Gower类功能性反应的时滞捕食系统模型。主要研究了系统中食饵种群的消极负反馈时滞对系统稳定性的影响。研究表明,当系统中食饵种群的消极负反馈时滞足够小时,即 τ∈ [0,τ0)时,系统处于一种理想的稳定状态;而一旦时滞的取值超越了临界点τ0,则系统将失去理想的稳定状态,在一定的条件下,食饵种群和捕食者种群将以周期震荡形式共存。文献[10]只考虑了系统中捕食者种群的妊娠时滞对系统稳定性的影响,本文继续考虑了系统中食饵种群的消极负反馈时滞对其稳定性的影响,因此本文所得结果是对文献[10]工作的一点补充。
参考文献:
[1]刘娟,孙礼俊.一类两种群均具有收获率的时滞捕食系统模型[J].蚌埠学院学报,2015,4(1):31-33.
[2]张蓬霞.一类带疾病的具有Holling III功能反应的捕食系统稳定性分析[J].山西大同大学学报:自然科学版,2015,31(2):13-15.
[3]王玲书,张雅南,冯光辉.一个具有时滞和阶段结构的比率依赖型捕食系统的稳定性[J].工程数学学报,2016,33(2):138-150.
[4]XU R.Globalstability and Hopfbifurcation ofa predator-prey model with stage structure and delayed predator response[J].Nonlinear Dynamics,2012,67(2):1683-1693.
[5]CHANG J X.Permanence and asymptotically periodic solution of a delayed predator-prey system with Holling-type IIfunctionalresponse [J].Mathematica Applicata,2015,28(4):925-932.
[6]吴万勤.一类时滞Lotka-Volterra系统的概周期解[J].云南民族大学学报:自然科学版,2017,26(2):130-136.
[7]杨喜陶.一类时滞捕食-食饵系统的概周期解的存在唯一性和全局吸引性[J].生物数学学报,2016,31(4):527-537.
[8]BEDDINGTON J R.Mutual interference between parasites or predators and its effect on searching efficiency[J].Journal ofAnimal Ecology,1975,44(1):331-340.
[9]DEANGELIS D L,GOLDSTEIN R,O’NEILL R V.A model for trophic interaction[J].Ecology,1975,56(4):881-892.
[10]UPADHYAY R K,AGRAWAL R.Dynamics and responses of a predator-prey system with competitive interference and time delay[J].Nonlinear Dynamics,2016,83(1):821-837.
[11]HASSARD B D,KAZARINOFF N D,WAN Y H.Theory and Applications of Hopf Bifurcation[M].Cambridge University Press,Cambridge,1981:43-49.
