浅析海底管道在内检测期间的振动问题

刘俊甫

(中国石化长输油气管道检测有限公司，江苏徐州 221008)

海底管道是海洋油气集输与储运系统的一个重要组成部分。管跨的出现改变了海底管道在管跨段的载荷形式和应力状态,海水流经管跨时,可能产生周期性的漩涡泄放,导致管跨产生周期性的振动,即涡激振动。除了涡激振动，在海底管道检测过程中，检测器通过时也会产生振动，当外在振动频率与管道固有频率(自振频率)接近时，产生谐振，极易引起管道失效造成管道爆裂、撕裂等。因此研究海底管道内检测期间管道振动问题有重要意义。

1 涡激振动对海底管道的影响

1.1 涡激振动

海底管道出现裸露后，在波浪、潮汐的作用下，由于压差的变化，引起边界层剥离，造成尾流涡旋分离，并以一定频率释放涡旋。当尾流涡旋释放频率与管道自振频率一致或相近时，将可能引起管道谐振，这就是涡激振动。当该振动较大时，极易引起管道损害和撕裂，造成严重的后果。

1.2 海底管道涡激振动的产生

涡激振动是一种受迫振动，涡激振动的产生有两个主要条件：①管跨段：由于海潮侵蚀等原因，海底管线经常在海床表面出现，不直接接触海床的悬空管段；②海水对管跨段附近管道的冲刷：在一定条件下，水流流经管线时，管线的尾流区产生一定频率、交替释放的涡旋，导致管道振动，称为涡激振动，管道振动可能出现在横流方向和顺流方向，一般情况下，横流方向的振动要大得多，造成的后果也更为严重。如图1所示。

1.3 涡激振动经验公式

海底管道通常涡旋的泄放频率很低，甚至低于1 Hz，学术界经过大量研究，给出了经验公式，涡旋泄放频率定义为fs，则：

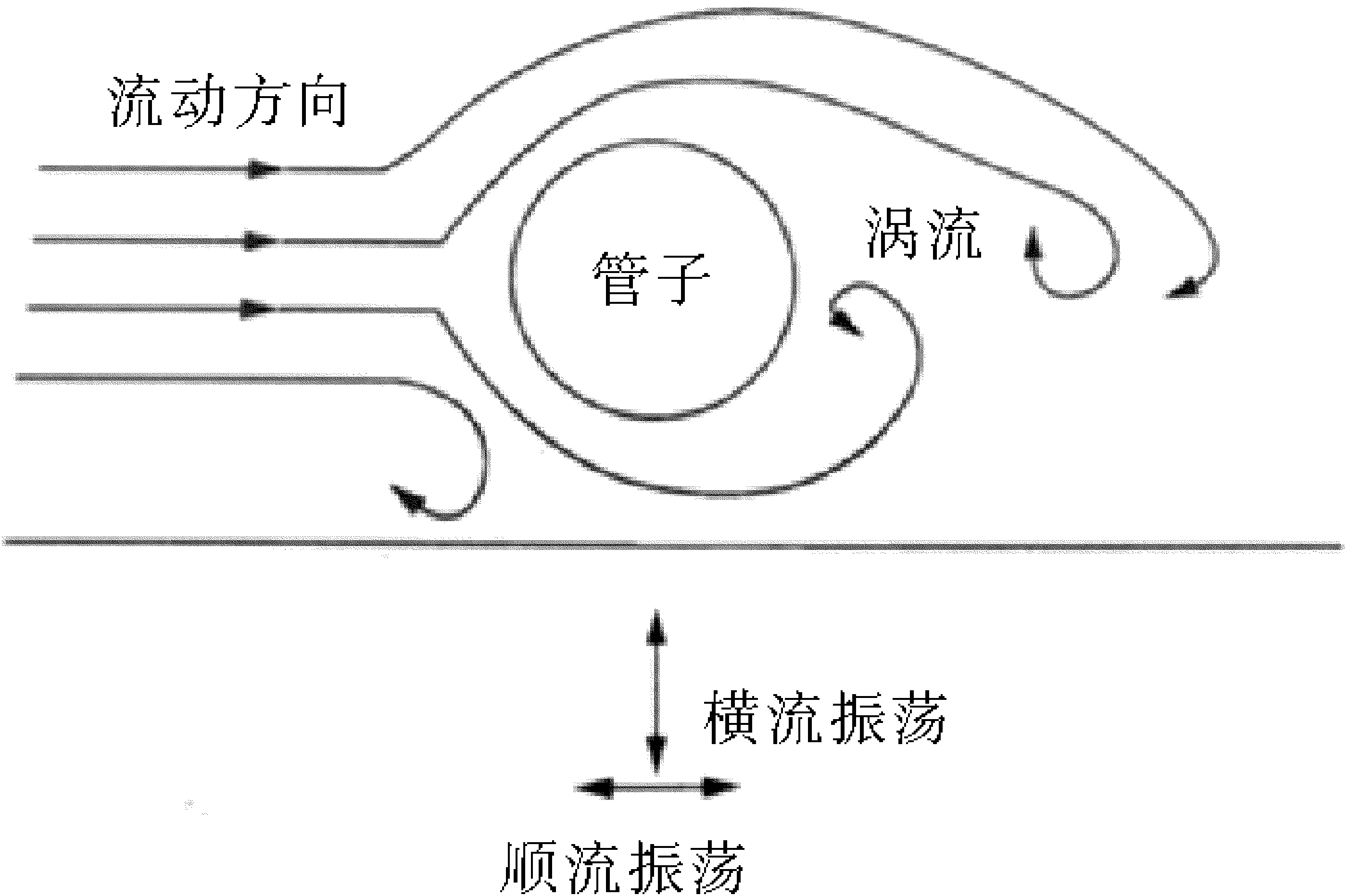
图1 海底管道涡激振动示意

(1)

式中：v0——流速；

St——斯特劳哈尔数，是流动雷诺数Re的函数；

D0——管道外径。

1.4 管道固有频率传统计算模型

管道固有频率传统计算模型是当海底管道出现悬空管段时，假设不考虑管道两端与海床耦合作用，即管道两端A、B两点为固定端，如图2所示。

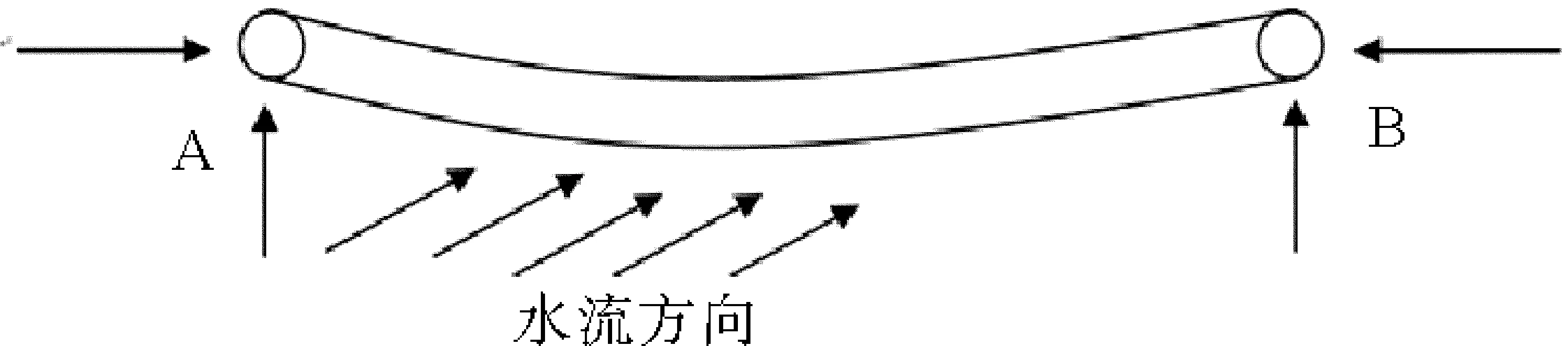
图2 海底悬空管道示意

由梁结构的振动分析得知，悬空管道的固有频率为[1]：

(2)

式中：fp——悬空管道的固有频率，Hz；

C——系数，当管道在水中振动时，C=0.7；当在空气中振动时,C=1.0；

K——与悬空管道两端支座条件有关的系数，当两端固定时K=4.73，两端铰支时K=3.14；如一端固定、一端铰支时，按照两端铰支计算；

l——悬空管道的跨长，m；

I——管道断面的惯性矩,m4；

E——管材的弹性模量,E=210 GPa；

Mp——管道单位长度的质量，计算时应包括管内含物及管外表防护加重层质量在内，kg/m。

1.5 基于ANSYS有限元分析的管道固有频率计算模型

目前对于管道固有频率的计算，一般使用ANSYS有限元分析软件，建立管土作用的非线性有限元模型进行计算。

基于ANSYS有限元分析软件建立管土作用的非线性有限元模型,管线结构采用浸没管单元PIPE59模拟。借鉴海洋平台桩基的处理方法,计算管跨入土段与土壤之间的非线性作用力,并以非线性弹簧单元COMBIN39模拟管、土之间的相互作用力[2]。建立的管土耦合模型考虑了管、土之间的耦合作用,如图3。

图3 ANSYS管土耦合模型

管道某阶固有频率即自振频率与管道悬空段长度和耦合土壤抗剪切强度有关，其关系曲线见图4和图5。

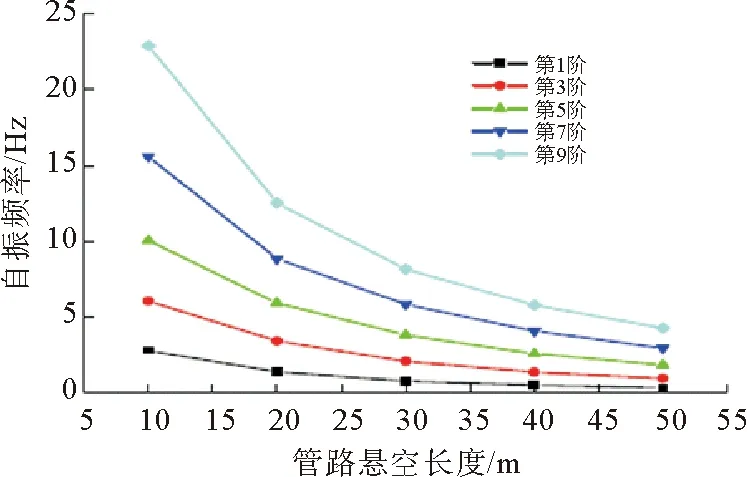
图4 管跨段长度与自振频率的关系曲线

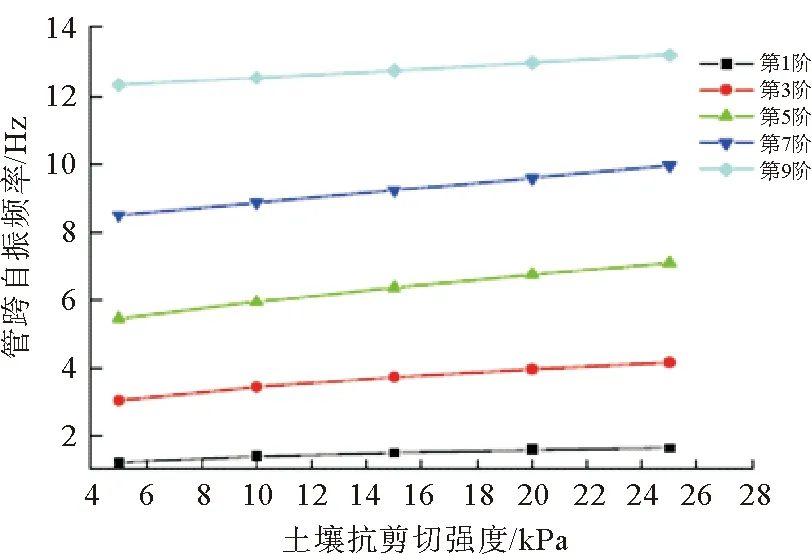
图5 耦合土壤抗剪切强度与自振频率关系曲线

由图4可以看出，悬空长度对管跨的自振频率影响很大，管跨的自振频率随悬空长度的增加呈指数函数衰减趋势；由图5可以看出，土壤抗剪切强度影响管跨的自振频率，二者关系图呈线性，土壤越硬，管跨的自振频率越大。

涡激振动最主要的能量输出集中在一阶部分，通常只有一阶涡激振动可能导致涡激共振，一阶振动通常发生在1 Hz附近的超低频区域，因此，该实验及其检测方法主要模拟管跨段一阶涡激振动模型如图6。

因此，选取一阶自振频率作为管道的固有频率fp，来进行管道振动频率的计算。

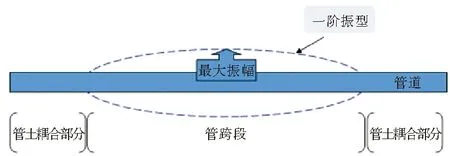
图6 一阶涡激振动模型

1.6 涡激共振

当涡旋的泄放频率接近当前管道的某阶固有频率时，将发生共振，此时振动释放的能量呈指数增长，导致二次应力聚集急速增加，破坏能力也显著增加。通常共振的发生条件公式是：

fs=(0.8～1.2)×fp

(3)

式中：fp——当前管道的某阶固有频率；

fs——涡激振动频率。

当涡激振动频率fs值在0.8～1.2倍的管道的某阶固有频率fp时，工程上认为管道将发生共振。

当涡激共振发生，管线受的切向应力急剧增加，如图7所示。

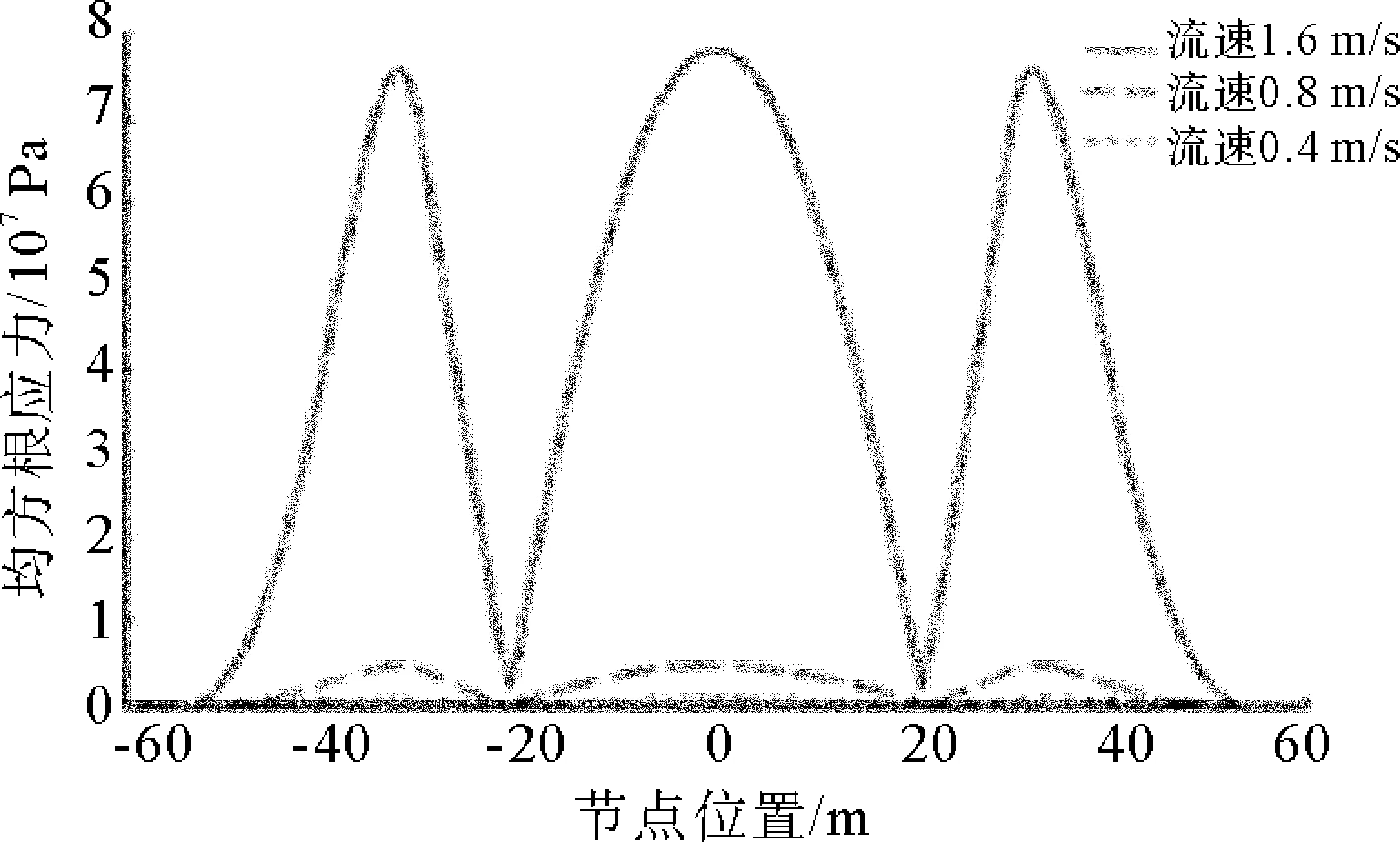
图7 涡激振动应力示意

图7为仿真计算的结论，仿真的管跨60 m，当流速达到1.6 m/s，发生共振。此时管跨中点和两端受力最大，即正负30 m附近达到应力积累的最大值。

2 管道内检测时的振动情况分析

管道内检测期间，当检测器通过被检管段时，必然引起管道的振动，而对于埋地管道或者管道两端进行固定时，这种振动趋势几乎为零；通过悬空管段时，这种振动则较为明显。当检测器通过某监测点的过程中，附耳贴在管壁上能清晰地听到有规律的撞击声，这是由检测器皮碗与焊缝的摩擦振动造成的。而该振动分为两种情况，分别是检测器皮碗与管节前后环焊缝摩擦振动和检测器前后皮碗与环焊缝摩擦振动。下面对这两种情况分别进行分析。

2.1 检测器皮碗与管节前后环焊缝摩擦振动

管节与管节之间采用焊接方式，检测器在管道内运行时，皮碗与焊缝摩擦产生振动。如图8所示假设每段管节的长度为l0，检测器速度为v1，检测器通过前后环焊缝时产生的振动频率f1应为:

f1=v1/l0

(4)

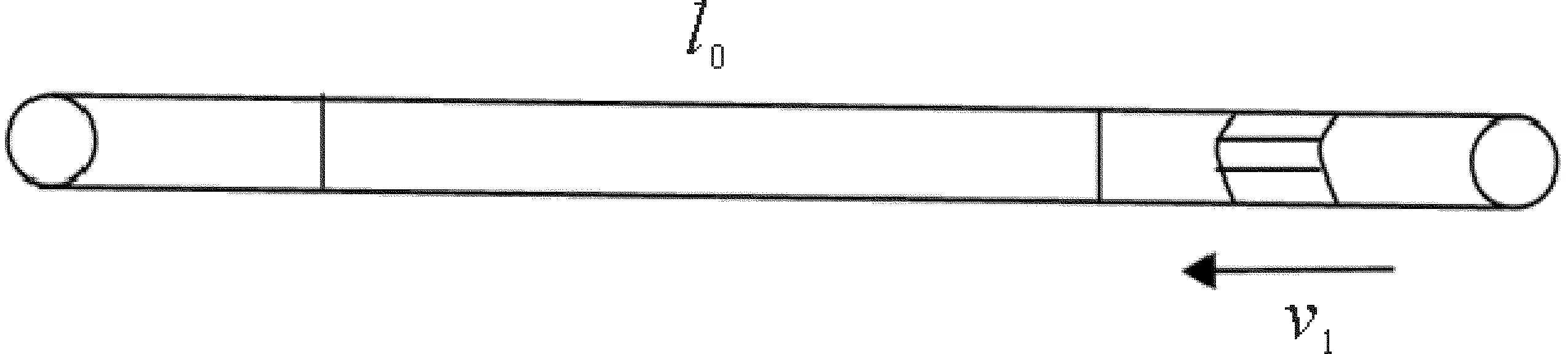
图8 检测器在管道内运行示意

2.2 前后皮碗与焊缝之间摩擦振动

皮碗之间是有一定距离的，当通过同一个焊缝时，即会出现前后摩擦振动。如图9所示，假设皮碗间距为l1，检测器通过速度为v1。这种情况下的振动频率f2为：

f2=v1/l1

(5)

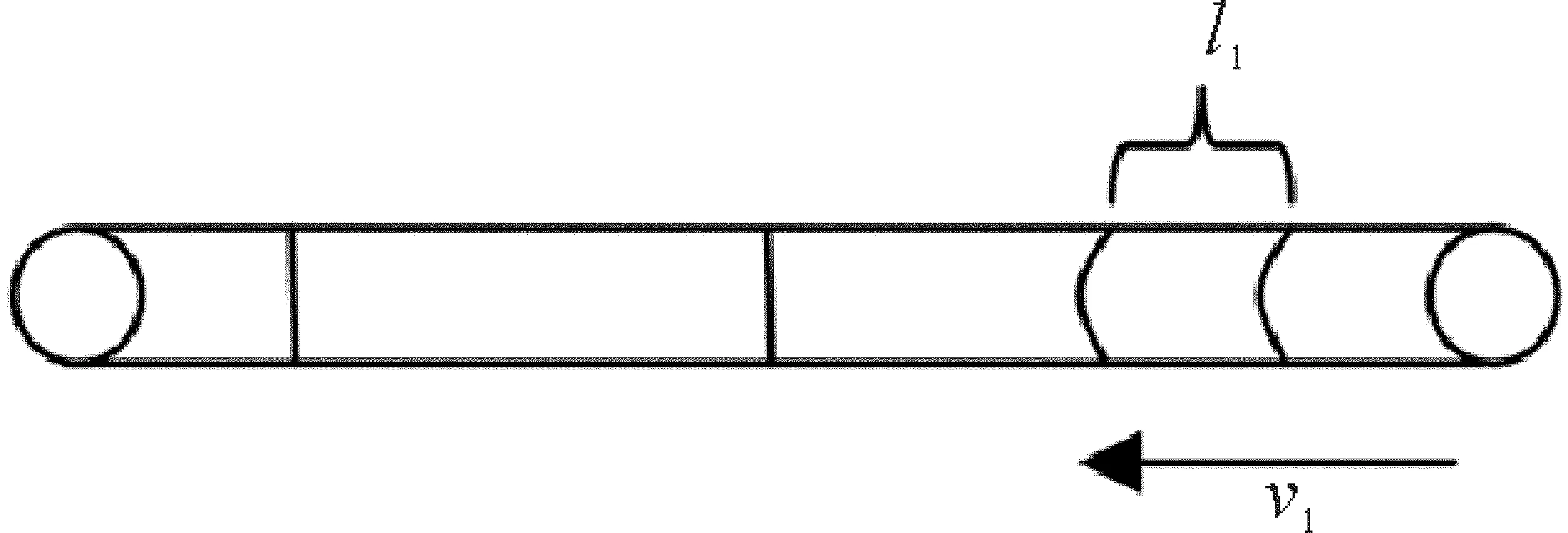
图9 皮碗间距摩擦振动示意

3 振动叠加

当海底管道出现悬空时，则在该处将出现来自管道外的涡激振动，而当该管段进行检测过程中，也将出现来自管道内的振动。那么最终管道内外振动将会进行叠加。

目前国内外均没有明确的公式进行准确计算，笔者根据多年的实践经验、结合国内专家们的指导，采用较易理解的线性叠加进行计算，该计算结果可用于定性分析。

根据以上分析，现将式(3)稍作修改变为式(6)和式(7)：

fs±f1=(0.8～1.2)×fp

(6)

fs±f2=(0.8～1.2)×fp

(7)

4 应用实例

某输油管线材质为X60，管径为762 mm，陆地管道壁厚8.9 mm，海底管道壁厚17 mm，材料弹性模量210 GPa，屈服强度415 MPa，泊松比0.3，材料密度7 850 kg/m3，防腐层厚度0.7 mm，防腐层密度1 445 kg/m3,内部流体密度856 kg/m3，底层海流流速0.95 m/s(季节变化)；假设悬跨长度30 m，检测器通过速度1.5 m/s(即输送介质流速)，管节长度12 m，皮碗间距1.1 m。

4.1 计算管道固有频率

建立管土耦合模型，研究悬空长度及耦合土壤的抗剪切强度对管跨自振频率的影响，采用ANSYS有限元分析软件建立管土非线性作用的有限元模型，进行模拟计算。

由ANSYS有限元分析计算可知，软性淤泥情况下，30 m悬跨，一阶自振频率fp为0.643 Hz，确定危险区间在0.52～0.77 Hz。

4.2 计算涡激振动频率

根据式(1)计算得出fs=0.249 Hz

4.3 计算检测器通过时的振动频率f1、f2

根据式(4)、式(5)计算得出f1=0.125 Hz,f2=1.364 Hz。

4.4 管道内外振动线性叠加分析

根据式(6)、式(7)计算得出：

fs±f1=0.124～0.374 Hz

fs±f2=1.115～1.613 Hz

根据上述计算得出最终线性叠加后的振动频率不在发生共振的危险区间，此时管道进行内检测时管道不发生共振。

5 结论

通过对内检测期间引起管道振动的主要因素进行研究，定性分析并理论给出计算过程分析是否会引起共振。检测期间主要通过以下方式避免引起管道共振。

a)一般情况下，管道所处的流速在每年的某时期是固定的，而与雷诺数相关的斯特劳哈尔数也为固定值，通常取0.2，这样涡旋的自激振动频率fs也是固定的。那么要想避免出现涡激共振，最有效的方法就是改变管道自振频率fp。而海底管道铺设结束后其断面结构已定，改变管道自振频率fp最直接的方法就是控制管道悬空段跨度来防止共振的发生。

b)当检测器通过悬空管段的速度不同时，引起的管道振动频率不同，那么应当计算出引起管道共振的速度区间，并使检测器的运行速度远离该区域。

c)因为在每年的不同时期内，洋流的流速和方向是不固定的，因此应当对不同季节的洋流引起的管道振动进行定量分析，并结合检测器的速度运行区间，给出最理想的检测时间。

d)要想避免共振，最有效直接的方法就是避免管道出现悬空管段。因此每年对海底管道的检测并掌握管道裸露和悬空信息是很有必要的，如果能进行整治杜绝出现管道的裸露与悬空，那么在检测过程中将不会出现管道共振引起的管道撕裂等状况。

[1] 帅健，于桂杰.管道及储罐强度设计[M].北京：石油工业出版社，2006:106-107.

[2] 时米波,陈国明,孙友义.基于管土耦合模型的海底管道管跨涡激振动分析[J].石油矿场机械,2007(10):5-8.