偶数阶微分系统主次特征值之比的下界
2018-05-02黄振明
黄振明
(苏州市职业大学 数理部,江苏 苏州,215104)
在由物理学、力学和工程技术等学科推出的微分方程(组)特征值问题中,人们常需找出最小特征值或次小特征值,因为这些低阶特征值在实际问题中有着明显的物理指征,常与物体的主要振动频率、物体弯曲变形的临界值等有关,尽管一般情形下很难求得其精确值,但对低阶特征值的分析和估计仍是很具实际意义的一个研究方向,近年来,国内外许多数学工作者从不同角度,运用分析、算子、嵌入数估计等方法在此领域进行了大量研究,取得了一系列成果[1-13],其中文[1]给出了有界开区间(a,b)上仅由两个方程构成的六阶微分系统特征值问题:
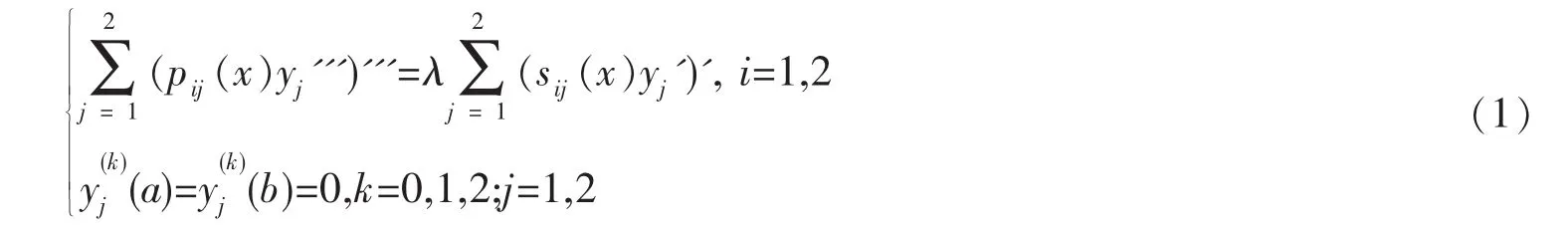
并得到了用主特征值λ1来估计次特征值λ2的上界不等式:

其中正实数 σi,τi(i=1,2)满足:对任意的实数 ξ1,ξ2有

本文考虑从两个方面将文[1]中的方程组(1)进行推广,一、方程个数为任意多个,二、方程阶数为任意偶数阶,即如下形式的微分系统:
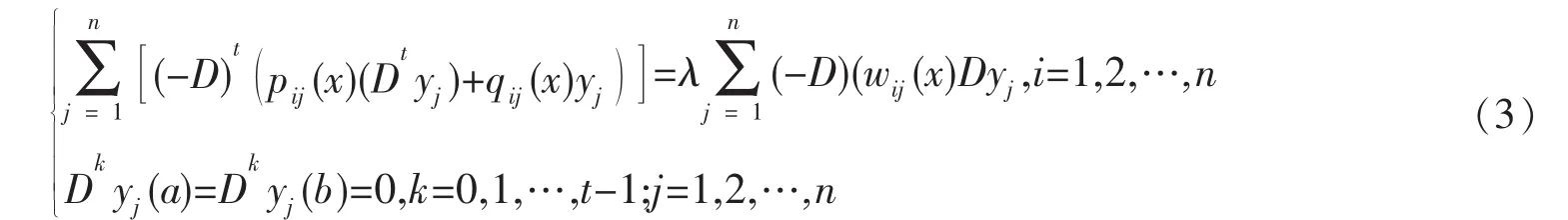
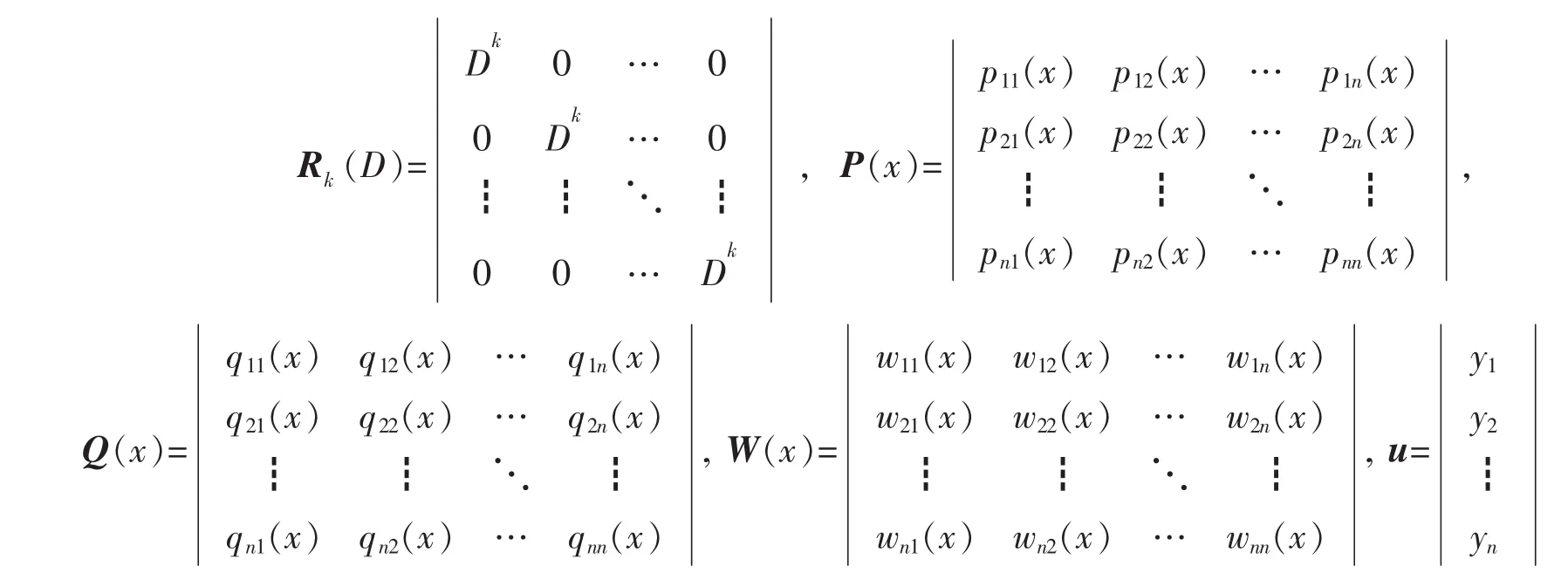
则可将系统(3)写成如下等价的矩阵形式

且满足如下正定或半正定条件:对任意 n 维向量有 ξ=(ξ1,ξ2,…,ξn)T∈Rn
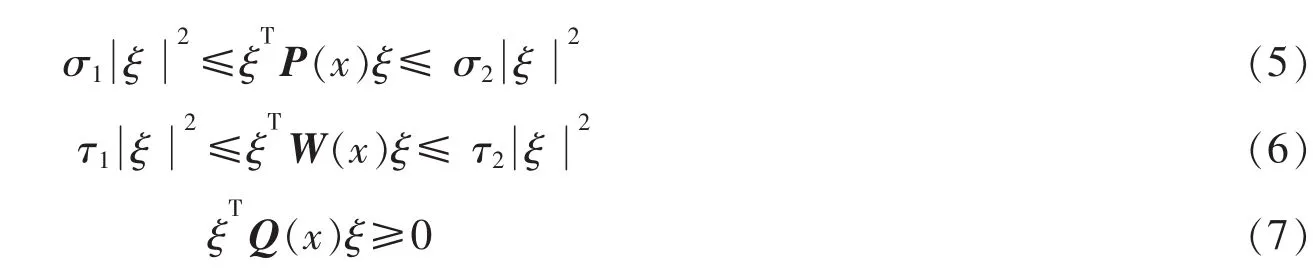
上述 σi,τi(i=1,2)均为正常数,T 为转置符号。
笔者参照并改进文[1]中的讨论方法,将[1]中的结论(2)推广至如下的一般情形。
定理 1设 λ1,λ2分别是问题(4)的主、次特征值(0<λ1≤λ2),则有

2 定理的证明
设问题(4)的主、次特征值分别为λ1,λ2在上述假定条件下,根据微分算子特征值理论知,λ1,λ2不仅是实的,而且是非负的,即0<λ1≤λ2,又记主特征值λ1对应的特征向量为u,且满足
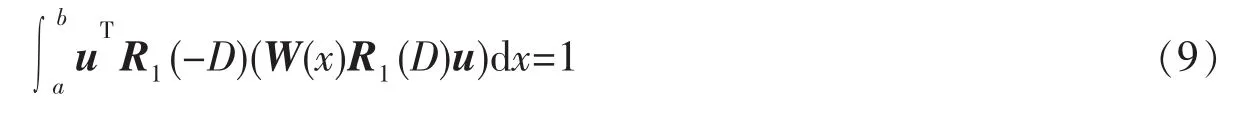
对式(9)运用分部积分,有
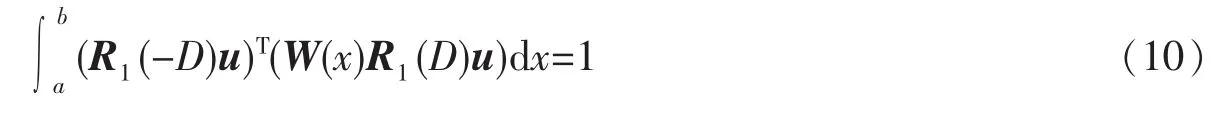
由式(10)和(6),得

从问题(4),利用分部积分和式(9),并注意到问题(4)中的边界条件可推得
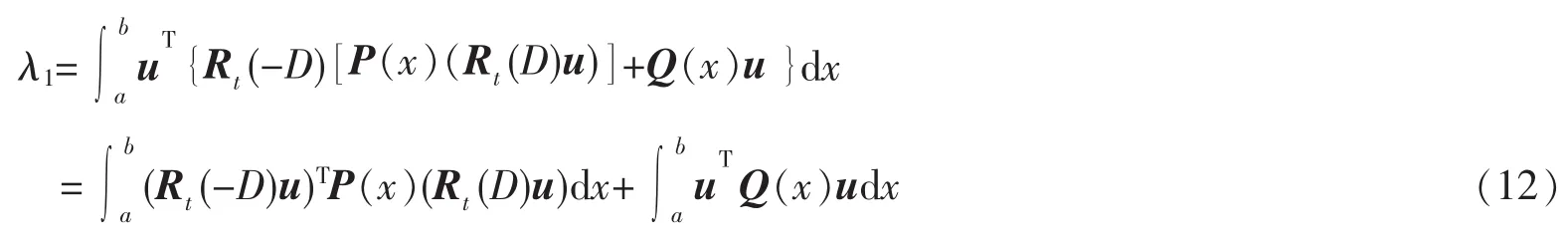
利用式(5)、(7)和(12),得

利用分部积分、φ的定义和式(10),计算得
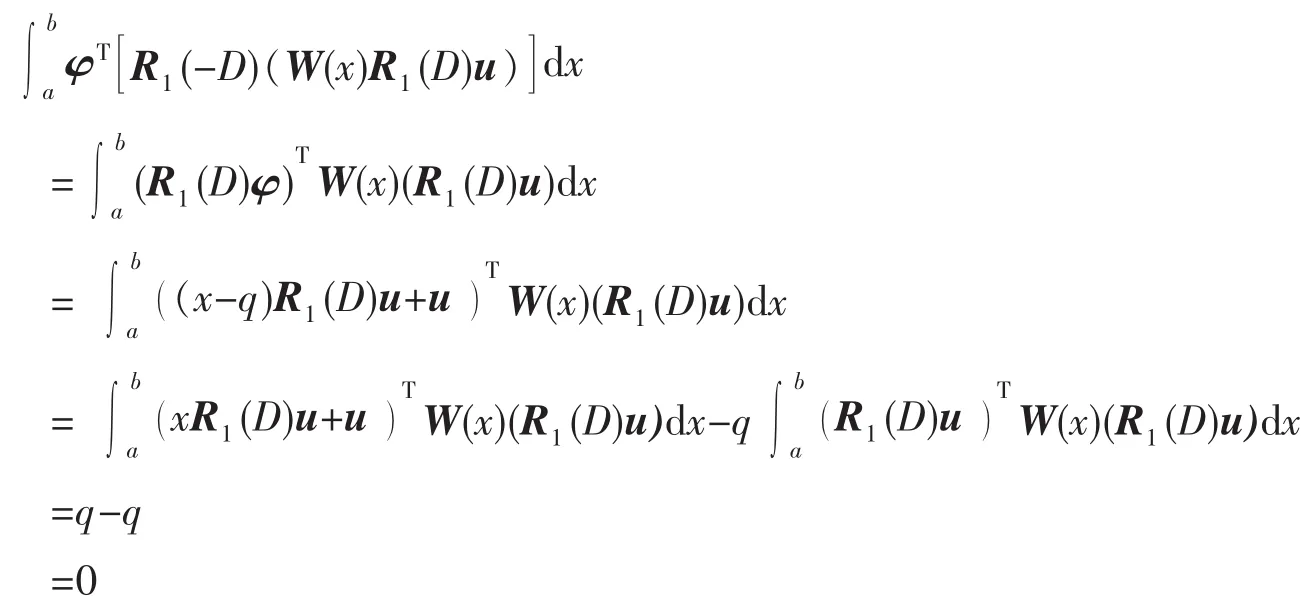
由此可知,φ与u广义正交,同时φ满足奇次边界条件:

根据变分法中的Rayleigh原理知,对所有与最小特征向量u广义正交、且满足奇次边界条件的连续函数φ所得瑞利商的最小值是次小特征值,由此得到下列不等式

利用φ的定义和式(4),计算可得
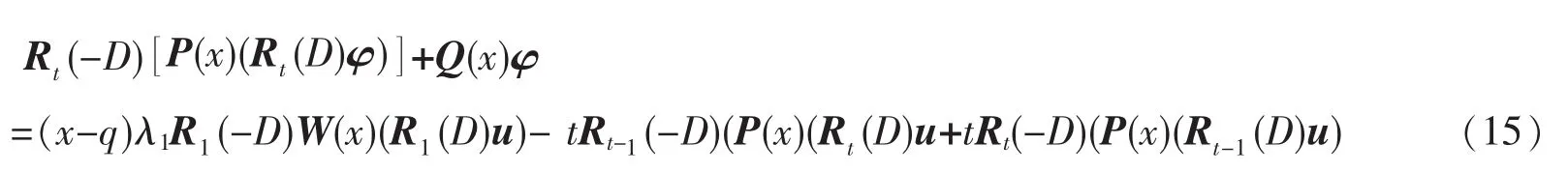

将恒等式(x-q)R1(D)u=R1(D)φ-u代入式(16)右端可得

再由式(15)和(17)可得
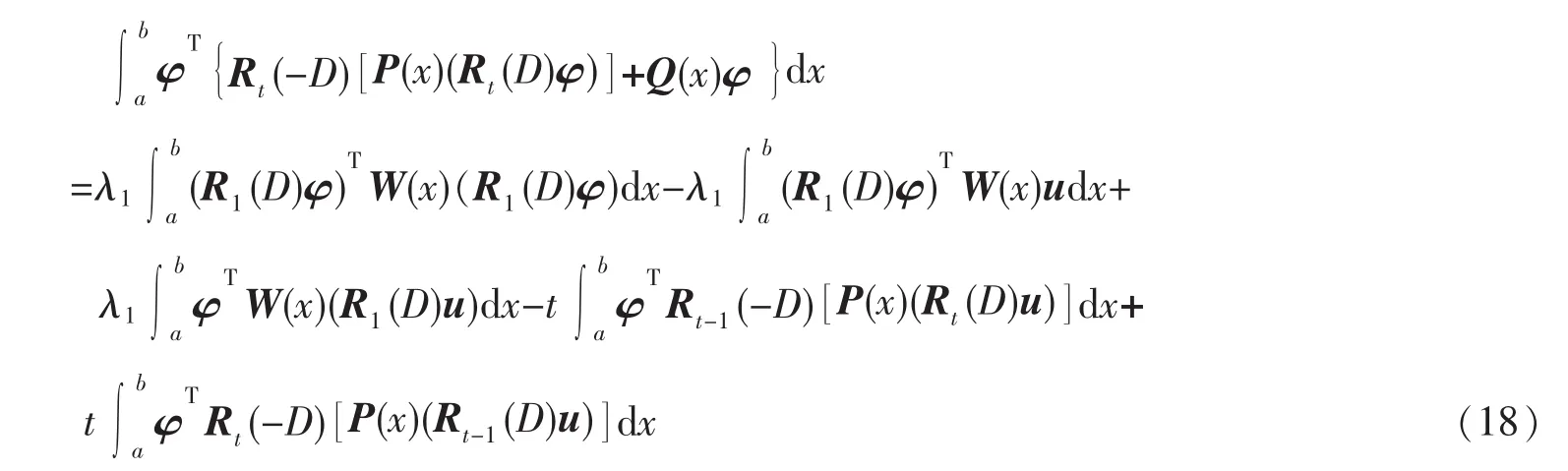

于是,利用式(14)、(18),有

即

引理1设u是问题(4)对应于主特征值λ1的特征向量,则
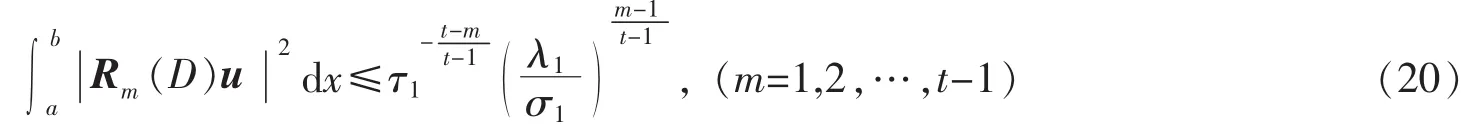
证明:先证明下列不等式

假设 m=k≤t-2 时,不等式(21)成立,即

则当m=k+1≤t-1时,利用分部积分,Schwarz不等式和上式,并注意到问题(4)中的边界条件得

整理上式,即得

即当m=k+1时,不等式(21)也成立,所以不等式(21)成立。
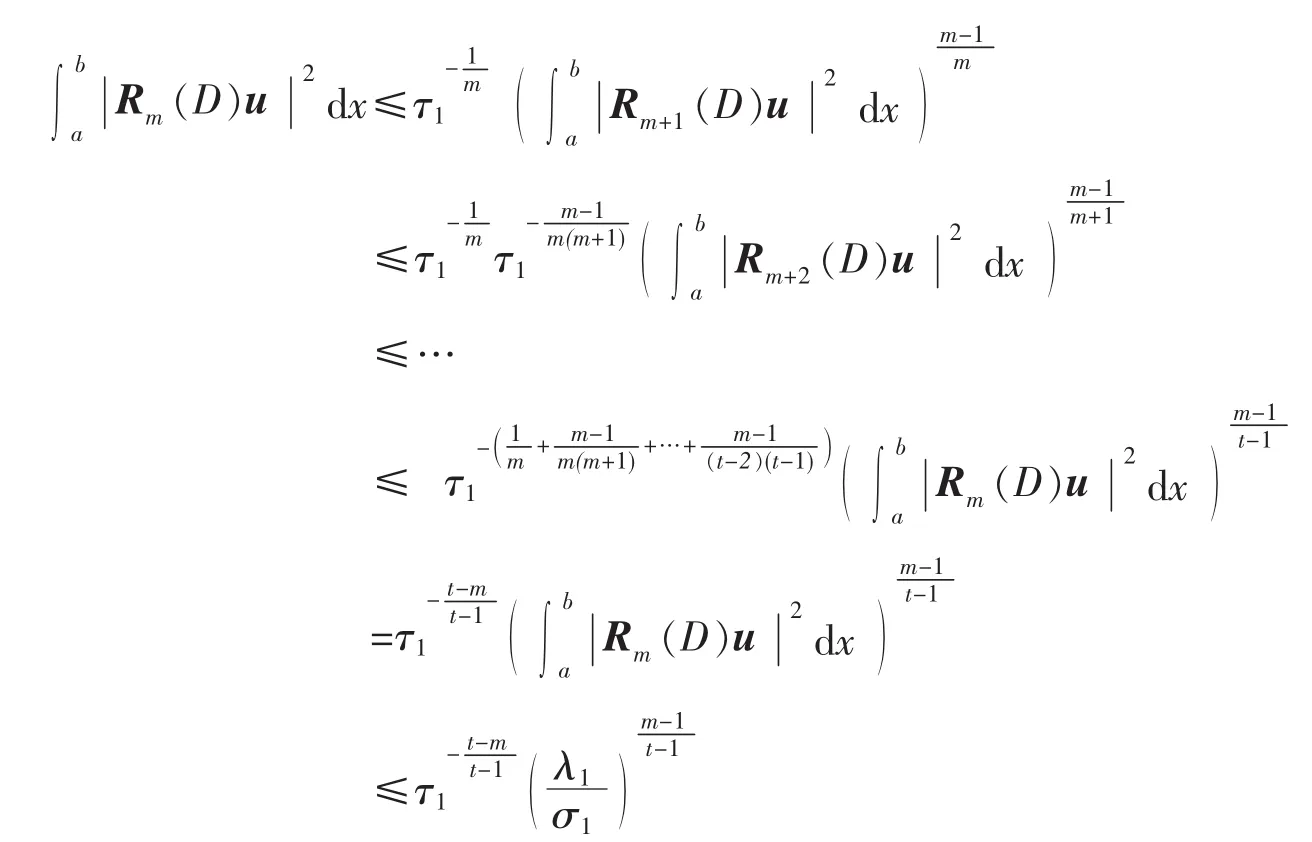
即证得引理1的式(20)成立。
引理2设λ1是问题(4)的主特征值,则当t≥3时,下列两不等式成立。

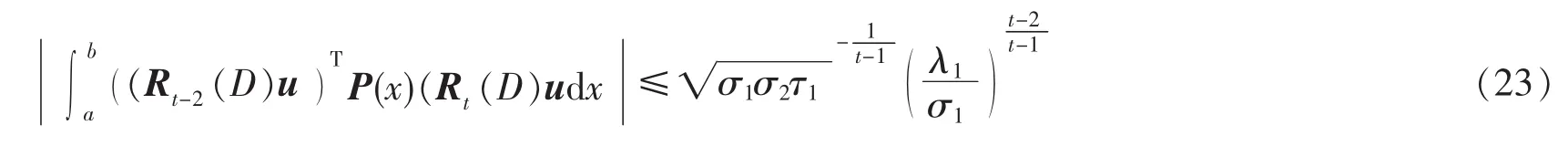
证明:利用式(11)、分部积分和Schwarz不等式得

由式(24)和引理1可得
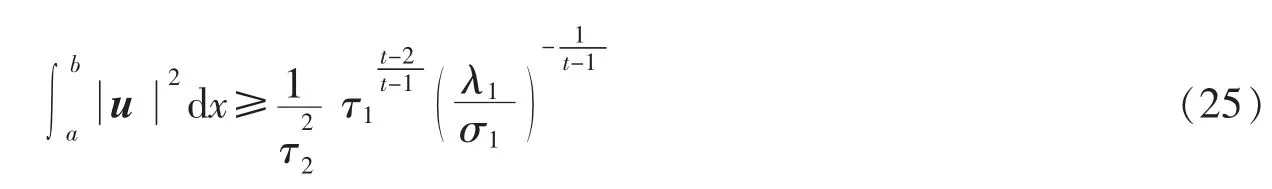
由式(6)和(25)即得引理 2 中的(22)。
利用 P(x)的正定性、式(5)、(12)和引理 1 得

即得引理2中的(23)。
引理3对于上述I,有如下估计上界

证明:利用φ的定义和分部积分法,逐项计算可得

合并式(27)和(28),恰好消去其中的不可控项,得
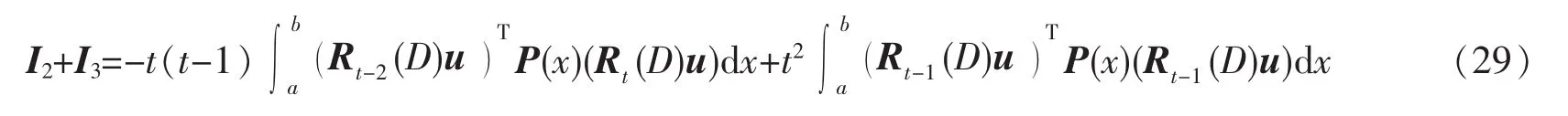
再根据引理 1、引理 2、(26)和(29)有

即得引理3。
引理4对于本文定义的试验函数φ,成立着不等式

证明:利用φ的定义和分部积分,
有

由式(30)得

利用式(11)、(31)、Schwarz不等式、(6)和引理 1,
有

化简即得引理4。
利用引理3和引理4,从式(19)可得
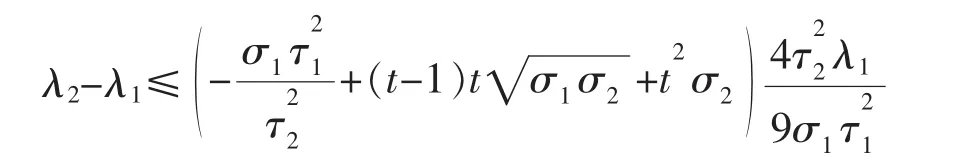
化简便得定理1中的式(8)。
3 结语
本文在六阶微分系统(1)的低阶特征值估计基础上,推广考虑了偶数阶微分系统(4)的特征值估计,获得了主、次特征值之比的下界估计不等式,其估计系数与所论区间的度量无关,特别地,文[1]讨论的系统(1)仅是本文系统(4)当 t=3,n=2,Q(x)=0时的特例,此时按本文的结论(8)对(1)成立着

与文[1]作者对(1)的估计结论(2)相比可知,本文用λ1估计λ2的上界比文[1]的相同估计减小了,或者说至少减小了λ1,因此,本文的估计结论比文[1]的更精确,在特征值问题中有着一定的参考价值。
参考文献:
[1]赵晓苏,钱椿林.六阶微分系统带权第二特征值的上界[J].长春大学学报(自然科学版),2010,20(8):10-13.
[2]刘景麟.常微分算子谱论[M].北京:科学出版社,2009.
[3]周敏,向会立.Neumann边条件下薛定谔算子前两个特征值间距的估计[J].湖北民族学院学报(自然科学版),2010,28(1):53-56.
[4]杨晓华,钱椿林.高阶一致椭圆型算子带权第二特征值的上界估计[J].中国科学技术大学学报,2013,43(6):461-465.
[5]黄振明.2s和 2t阶联立微分方程组次特征值的估计[J].海南师范大学学报(自然科学版),2015,28(3):250-254.
[6]杨贵诚,侯兰宝,杜锋.Carnot群上低阶特征值的估计[J].扬州大学学报(自然科学版),2016, 19(2):10-12.
[7]SHI J H.Estimates for Lower order eigenvalues of a class of operators on riemannian manifold[J].J of Math (PRC),2015,35(4):809-816.
[8]HOOK S M.Domain independent upper bounds for eigenvalues of elliptic operator[J].Trans Amer Math Soc,1990,318:615-642.s
[9]MARK S A.The universal eigenvalue bounds of payne-polya-weinberger,hile- protter,and H C Yang[J].Proc Indian Acad Sci(Math Sci),2002,112(1):3-30.
[10]MOHAMED EI GAMEL,MONA SAMEEH.An efficient technique for finding the eigenvalues of fourth-order sturm-liouville problems[J].Applied Mathematics,2012(3):920-925.
[11]CARSTEN CARSTENSEN,DIETMAR GALLISTL.Guaranteed lower bounds for the biharmonic equation [J].Numerische Mathematik,2014, 126(1): 33-51.
[12]SIMON RAULOT,ALESSANDRO SAVO.Sharp bounds for the first eigenvalue of a fourth-order steklov problem[J].The Journal of Geometric Analysis,2015,25(3):1602-1619.
[13]SHUICHI JIMBO.Eigenvalue of the laplacian in a domain with a thin jubular hole[J].Journal of Elliptic and Parabolic Equations,2015,1(1):137-174.
