高庙子膨润土抗剪强度预测模型研究
2018-05-02蔡清池
蔡清池 ,崔 明 ,刘 春
(1.宁德师范学院 信息与机电工程学院,福建 宁德 352100;2.中交隧道工程局有限公司,北京 100102)
土力学参数的研究是岩土工程的一个重要课题,为土体的力学性质或破坏机制判别以及土体渗流稳定性分析提供了不可或缺的基础数据。库仑提出了土体剪切强度的计算方法,认为土体剪切强度主要由两大影响因素:一是颗粒之间的粘聚力,二是与法向正应力相关的内摩擦角[1]。基于此观点,库仑提出了评价土体剪切强度的指标粘聚力c和内摩擦角φ,引起了人们的广泛关注。目前,有不少学者着重研究了剪切速率或岩体节里裂隙等对岩土体抗剪强度大小的影响,具有一定的理论和实验基础[2-5]。也有学者针对土体中含水量对粘性土的影响开展了研究[6-7]。但关于内摩擦角、粘聚力与土体其它固有属性参数(如弹性模量Es、土体密度ρ)之间的关系,目前仍研究尚少。研究表明,土的组成和土的孔隙比等自身因素对土的抗剪强度有着一定的影响[1,8]。土的组成主要表现在土体的三相物理指标上。考虑膨润土主要应用于地下深部环境,同时根据实际用途需要较高强度的干燥土体,此时膨润土为重塑土,因此研究土体在不同密度下或者不同实验条件下,粘聚力和内摩擦角大小的变化规律,有着重要的科研价值和工程意义。
本研究以内蒙古高庙子膨润土为基本研究对象,利用岩石三轴刚性试验机,探究单轴和三轴条件下不同压实密度和不同压实尺寸的高庙子膨润土的抗剪强度参数的变化规律,建立膨润土抗剪强度预测模型。
1 实验数据分析与归纳
本次试验共设计了3种土试样,均为圆柱形,规格分别为Φ50mm×100mm、Φ50mm×110mm、Φ50mm×120mm,每种土样设计4种密度 1.40、1.50、1.60、1.70 g/cm3,将土样烘干后在模具中一次压实成型,行程圆柱形试样。试样的密度范围在1.35~1.75 g/cm3之间。试验过程中,为更好模拟膨润土使用时所处的真实地压环境,将试样分别在围压为0、2.5、5、7.5、10 MPa下进行。单轴实验中试验机以每分钟0.2%的轴向应变速率加载,直至试样破坏;三轴实验中试验机以0.5 mm/min的速率进行加载实验。
图1为单轴实验下不同规格土样的密度与峰值应力之间的关系曲线。由图1可以看出膨润土的单轴抗压强度随土样密度ρ的增加有增大趋势。当密度ρ由1.4 g/cm3增大至1.7 g/cm3时,单轴抗压强度由约0.5 MPa增长至3.0 MPa左右,增幅比较明显。对比3种规格的土样,可见土样的密度范围在1.35~1.75 g/cm3之间时,单轴抗压强度σ1的增长速率有如下变化趋势:首先σ1以速率k1增长,在约ρ=1.53 g/cm3时σ1有极大值,而后以速率k2增长,在约ρ=1.65 g/cm3时,σ1有另一极大值,此后大约以速率k3增长。其中k3≥k2≥k1。由于对于同一个试样,依据莫尔库仑强度准则,试验峰值剪切强度τf与正应力σ1成正比函数关系,因此图1亦反映出膨润土剪切强度与土样密度之间的变化关系。
基于以上图形分析,可以认为对于膨润土来说,在1.35 g/cm3≤ρ≤1.75 g/cm3时,σ1可以按照公式(1)进行计算。

因此,对图1中实验数据进行线性拟合和非线性拟合(拟合过程中忽略同高度土样尺寸间误差产生的影响),拟合结果见图2。对比拟合结果可以发现,三阶非线性拟合相比其他拟合方式有较好的拟合效果,其相关性系数为95.403%,而线性拟合下相关性系数为88.729%,而且由于多项式若拟合阶数越高,则相对低阶拟合来说拟合效果越好,但是从三阶拟合开始,四阶、五阶和三阶的拟合曲线基本重合,因此可以说三阶拟合曲线能较好的反映不同密度下单轴抗压强度的变化情况,这也验证了公式(1)的正确性。

图1 不同试样规格下σ1-ρ的关系曲线

图2 不同拟合方式下σ1-ρ的关系曲线
三轴实验下,观察图3~5,对比可得:相同围压下,土样的三轴抗压强度σ1随着土样高度h的增加有增大趋势。以σ3=5 MPa为例,在密度ρ=1.6 g/cm3,土样高度h由100 mm增加至120 mm时,三轴抗压强度σ1由14.03 MPa增大至16.67 MPa,增幅18.82%。此外,不同试样规格、相同围压下膨润土的三轴抗压强度随着密度的变化而呈现出多种变化趋势。鉴于实验数据中密度范围有限,依据之前对单轴实验的数据分析,笔者认为在密度较小情况下,膨润土的三轴抗压强度随着压实密度的增加呈现出增大趋势,当密度增加到某一数值时,此时有最大值,而后开始降低或者趋于某一固定值。
分析不同规格下膨润土的σ1-σ3关系曲线,可得相同密度下膨润土的三轴抗压强度随着围压的增大而增长。在此只给出了土样规格为50mm×100mm的σ1-σ3的关系曲线,见图6。在围压σ3≤5 MPa时,同一规格的膨润土样的三轴抗压强度σ1并未随着密度的增加而发生明显增长,当围压σ3>5 MPa时,随着密度的增加,σ1明显增大,而且ρ=1.5 g/cm3时,增长较大。
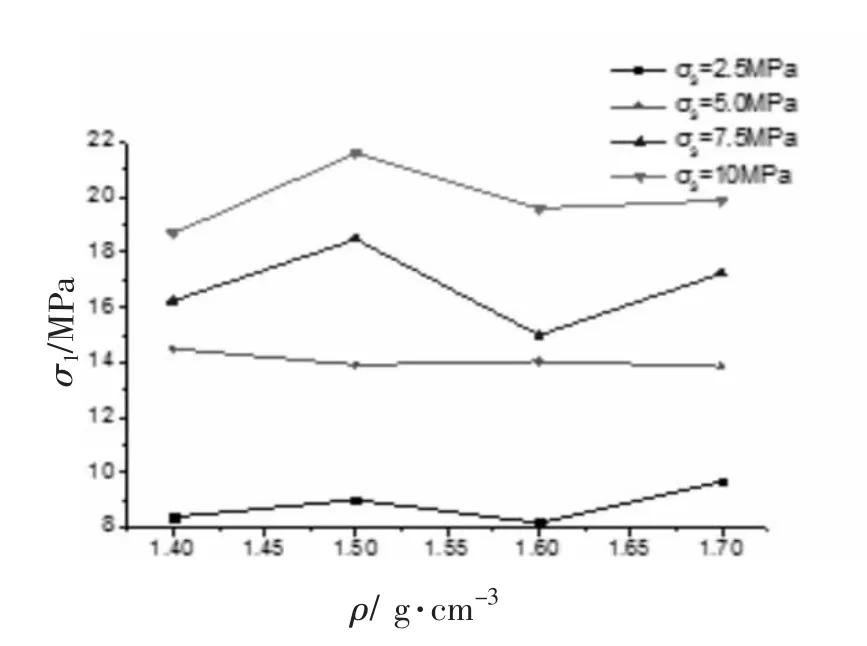
图3 不同围压下σ1-ρ的关系曲线(50×100)

图4 不同围压下σ1-ρ的关系曲线(50×110)
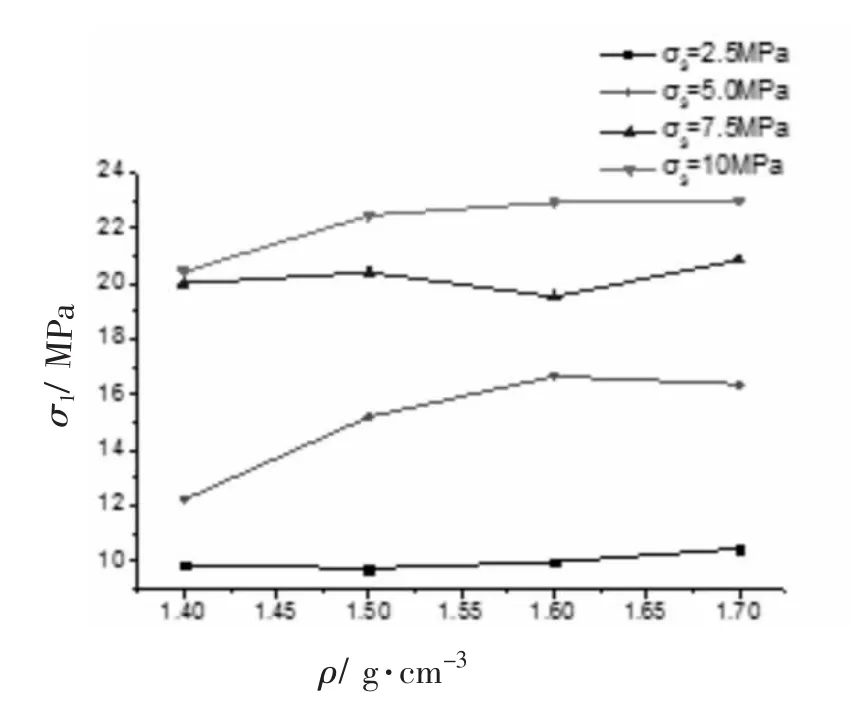
图5 不同围压下σ1-ρ的关系曲线(50×120)

图6 不同密度下σ1-σ3的关系曲线(50×100)
2 粘聚力与内摩擦角的回归计算与分析
由于三轴实验下,无法直接得出剪切面的主应力大小和剪切强度大小,从而不能直接进行线性拟合计算,因此可以通过“σ1-σ3”方法计算土体的粘聚力和内摩擦角[9-12]。文献[9-12]中对抗剪强度参数的两种回归分析方法进行了详细分析,认为“σ1-σ3”方法计算所得结果是真值的最佳估值。莫尔库仑准则下土体破坏强度包络线方程为:


因此:

对于A和b,通过文献[7]至文献[9]中提供的“σ1-σ3”方法进行线性回归计算。将计算所得的A和b分别代入公式(4)和公式(5)中,可得如下表1的数据。
由表1可见:对于相同规格的膨润土试样,粘聚力c随着密度ρ的增加呈非线性增长,而内摩擦角φ表现为先增大后减少或趋于不变的情况。如试样规格为50mm×100mm的土样,密度ρ由1.4 g/cm3增加为1.7 g/cm3时,粘聚力c增加43.75%,内摩擦角起初呈增大趋势,当密度为1.6 g/cm3时趋于不变。同理,当土样密度相同且试样直径大小不变而高度不同时,内摩擦角φ会在一定范围内浮动,但是变化趋势并未表现出一致性。
基于前面的分析,猜想试样高度h和密度ρ二者对试样剪切强度大小的影响为:高度h主要对内摩擦角φ产生影响,密度ρ主要支配粘聚力c的变化。并在此基础上开展了下一步分析。
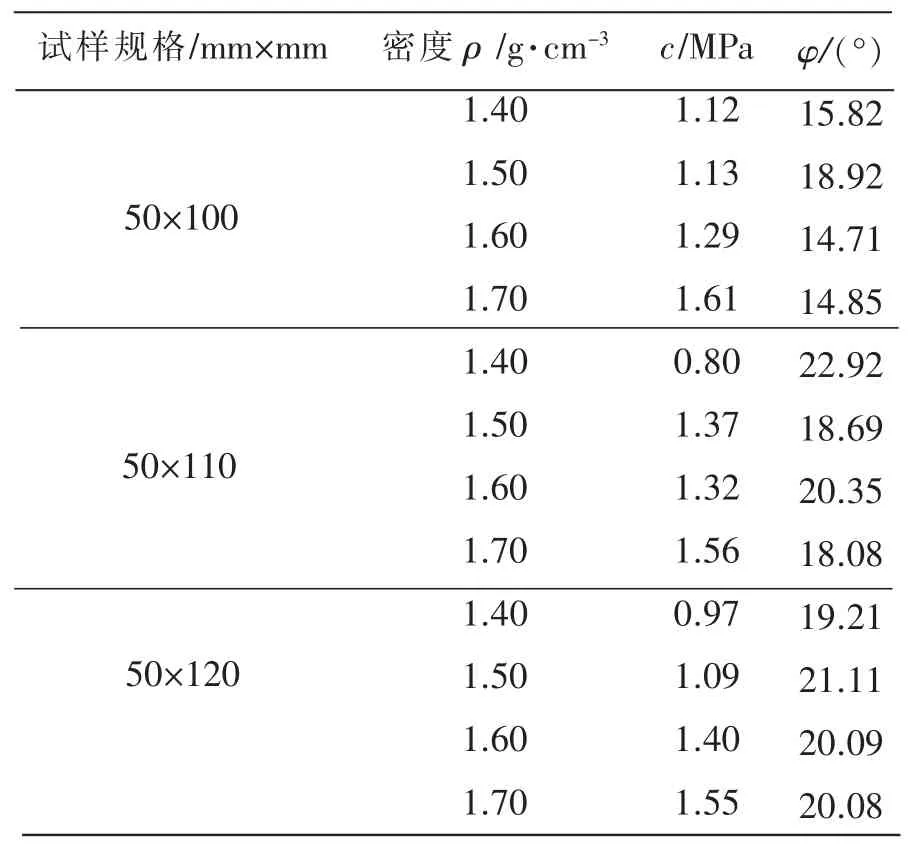
表1 粘聚力和内摩擦角的计算
3 高庙子混凝土抗剪强度预测模型
对于抗剪强度参数的研究,目的是建立膨润土的抗剪强度预测模型。莫尔库仑准则是岩土工程中应用广泛的强度理论之一,它阐述了土体剪切强度的影响因素和计算方法,认为土体抗剪强度可以按照公式(6)进行计算:

根据公式(6),主要根据内摩擦角和粘聚力的变化情况对膨润土的抗剪强度大小进行预测。基于前面的分析,引入函数f(h/100)和g(ρ/1),分别代表高度对内摩擦角φ和密度ρ对粘聚力c的作用曲线,此时 φ=f(h/100),c=g(ρ/1),。 其中,h/100 代表试样高度与标准规格下高度为 100 mm 的比值,ρ/1代表试样密度ρ与密度为1 g/cm3的比值。通过此种方式引入无量纲参数。借鉴单轴实验下峰值应力与密度大小间的拟合结果,采用幂函数进行参数拟合。根据上述的猜想:
令


依据表1中的数据对k、α进行线性回归。回归中采用相同密度下的数据分别进行分析。
根据关系拟合曲线得到膨润土的抗剪强度参数φ和c的确定性预测模型如下:
内摩擦角φ:

式中:h为直径为50mm的试样高度。
通过表2的分析可以发现,在试验密度为1.5~1.7 g/cm3时,内摩擦角与试样密度的拟合结合相关性系数较高,而密度为1.4g/cm3时拟合相关性系数为0.297 6,较低。但是考虑到试样密度为1.5~1.7 g/cm3时的结果,初步认为上述的猜想是较为正确的,从而认为公式(9)具备一定的准确性。该公式对于本次研究中针对试样高度100~120 mm的具备较好的适用性。因为实际应用中膨润土是储备在一定规格的金属内部,因此可以满足实际工程应用。
粘聚力c:

式中:ρ为试样的密度。
通过表3的分析可以发现,公式(10)具备良好的普适性。在试样高度为100~120 mm之间时,均获得了良好的拟合结果,拟合相关性系数高。该公式对于本次研究中的密度范围为1.4~1.7 g/cm3均适用。
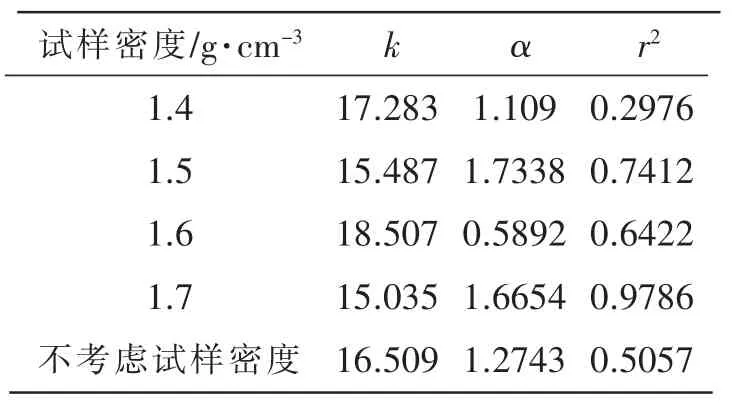
表2 内摩擦角相关方程系数回归值

表3 粘聚力相关方程系数回归值

4 结论
结合公式(9)、公式(10),将公式(6)改写为:
本文通过对大量室内实验数据进行分析,研究高庙子混凝土抗剪强度预测模型,得出如下结论:
(1)单轴条件下,膨润土的抗剪强度大小与土试样密度呈非线性关系,整体上随着密度的增大而增加。三轴条件下,对于具有相同的围压的土试样,其抗剪强度随着土体密度或者土试样高度的增大而增大。
(2)结合莫尔库仑准则,分析可得:室内实验下,由实验所得膨润土的内摩擦角和粘聚力与试样的高度和密度密切相关。猜想试样高度大小对内摩擦角变化起主要影响作用,对粘聚力影响较小。土体粘聚力随着试样密度的增大呈幂指数形式增加,内摩擦角大小基本不随密度的改变而变化。通过对膨润土试样的实验数据进行了分析,一定程度上验证了该猜想的准确性。
(3)室内实验下,膨润土试样的内摩擦角和粘聚力大小呈一定的函数关系,公式(9)和公式(10)均可作为参考,判定系数分别为0.5057和0.8032。因膨润土用途的特殊性,该公式中暂未考虑土体含水量大小对莫尔库仑参数的影响,但是对于研究土体密度、试样高度等材料固有特性对膨润土抗剪强度的作用效果仍然具有一定的适用价值。关于含水量大小对膨润土性质的影响,将在后续的工作中进一步研究。
参考文献:
[1]邹新军.土力学与地基基础[M].长沙:湖南大学出版社,2016.
[2]李海波,冯海鹏,刘博.不同剪切速率下岩石节理的强度特性研究[J].岩石力学与工程学报,2006(12):2435-2435.
[3]刘世伟,盛谦,龚彦峰,等.基于应力集中系数的抗剪强度取值方法及其应用研究[J].岩土力学,2017(s1):53-60.
[4]钟卫平,沈晓明.岩石节理剪切强度研究[J].武汉理工大学学报,2011(2):96-99.
[5]曾纪全,杨宗才.岩体抗剪强度参数的结构面倾角效应[J].岩石力学与工程学报,2004,23(20):3418-3425.
[6]LIU J,ZHANG H.Water content influence on properties of red-layers in Guangzhou metro line,China[J].Advances in Materials Science and Engineering,2017:1-12.
[7]刘纪峰,卢明师.含水率对边坡土性及其稳定性的影响[J].河南科技大学学报(自然科学版),2010,31(3):63-66.
[8]李广信.高等土力学[M].北京:清华大学出版社,2004.
[9]胡波,杨志荣,刘顺桂,等.共面闭合断续节理岩体直剪强度特性研究[J].工程地质学,2008(3):327-331.
[10]刘飞禹,王攀,王军,等.颗粒粒径对格栅-土界面静、动力直剪特性的影响[J].岩土力学,2017,38(1):150-156.
[11]陈立宏,陈祖煜,李广信.三轴试验抗剪强度指标线性回归方法的讨论[J].岩土力学,2005(11):1785-1789.
[12]陈立宏,陈祖煜,李广信.线性回归抗剪强度指标方法的改进[J].岩土力学,2007(7):1421-1426.
[13]余东明,姚海林,吴少锋.三轴试验抗剪强度参数值回归分析法的区别与修正[J].岩土力学,2012(10):161-166.
