异形柱框架结构抗震性能的ANSYS有限元分析
2018-05-02王军芳
王军芳
(1.三明学院 建筑工程学院,福建 三明365004;2.工程材料与结构加固福建省高等学校重点实验室,福建 三明365004)
异形柱框架结构是近年来一种新型节能住宅结构,具有柱楞不突出墙面、建筑观瞻性好、节约能源、增加使用面积及适应功能变化等优点,很受开发商及住户的欢迎[1-4]。由于该结构没有经受过地震考验,再加上异性柱多肢的存在,其剪力中心与截面形心往往不重合,导致柱肢混凝土受力时常先于普通矩形出现裂缝,脆性明显,变形能力较低等,因此,工程设计人员对其抗震性能非常关心。目前针对异形柱构件及异形柱平面框架结构性能的研究较多,而整体抗震性分析的研究成果较少,有关的结论只是些定性的分析,更多的抗震规律需要进一步的研究。本文对文献[5]振动台上完成的一个异形柱框架结构试验模型的原型进行模拟计算,探讨其在设防烈度和罕遇烈度下的整体抗震性能,进一步研究ANSYS作为异形柱框架结构弹塑性分析手段的可行性。
1 模型建立
采用有限元软件ANSYS对文献[5]中试验模型的原型即6层异形柱框架结构(平面图如图1)进行水平地震作用下的模拟分析。由文献[5]可知:地震设防烈度为8度(0.2g),Ⅱ类场地(第2组),二级抗震。异形柱截面形式见图1,柱肢长700 mm,肢厚250 mm,采用HRB400的钢筋,配筋情况1~2层L型柱均采用Ф22mm钢筋,T字型柱均采用Ф25mm钢筋,十字形柱均采用Ф18mm钢筋,3~6层所有柱纵筋均采用Ф18mm钢筋。柱混凝土C45,梁板混凝土C30,所有构件保护层厚度均取30 mm。
建模时,混凝土采用SOLID65单元模拟,钢筋通常用LINK8单元模拟,如图2。模型中不考虑钢筋与混凝土间的粘结滑移,即共同工作的计算精度能满足工程精度要求[6]。

图1 原型标准层柱网结构布置(单位:mm)

图2 计算模型(单位:mm)
梁柱单元模型根据文献7均采用考虑刚度退化的三线型恢复力模型(如图3),它能较好的描述钢筋混凝土异形柱构件非线性受力的全过程,其中模型的特征点根据实配钢筋计算。有限元模型及其网格划分情况以节点处十字形柱为例如图4,底层柱与基础刚接,不考虑基础与上部结构的共同作用。
为了较真实地体现地震作用下的结构地震反应,本模型选用与振动台试验模型一致的El-Centro南北向地震波(地震最大加速度为341.7 cm/s2)进行结果的对比分析。考虑到不同的地震波输入所得的时程分析结果也不同,但却不影响结构抗震反应的整体趋势,所以又分别输入南北向Taft波(地震最大加速度为152.7 cm/s2,)和人工拟合波(抗震设计规范[8]Ⅲ类场地8度二组5%阻尼比的反应谱进行拟合)2种地震波,进一步了解ANSYS在不同波形作用时结构的整体抗震反应是否一致。
2 计算结果验证
图5为El-Centro(南北向)地震波作用下的结构模型自振周期计算值的曲线与相应试验值曲线的对比情况图。由图可知:ANSYS计算模型的计算周期与振动台模型的试验结果吻合度较好,计算模型的低阶振型周期与试验值基本相同。分析说明,用ANSYS模拟异形柱框架结构的动力弹塑性分析具备可行性。

图3 三线型恢复力模型

图4 十字形柱有限元模型
3 计算结果分析
为了方便比较分析,选取各楼层处的相对位移最大值和楼层处的最大相对位移值曲线进行对比。图6~9分别给出了8度(0.2g)多遇烈度和罕遇烈度时,计算模型在El-Centro波(_el)、Taft波(_ta)和人工拟合波(_rg)分别作用下楼层相对位移最大值的计算值曲线图与El-Centro波作用下楼层相对位移最大值的试验值(_sy)对比曲线图和楼层层间位移最大值曲线对比图。
由图6~9可知,8度多遇烈度和罕遇烈度下,异形柱框架结构实际楼层最大位移的计算值和试验值的对比分可知,其位移曲线形状走势一致。其中El-Centro波(_el)作用下的计算模型值与试验值的曲线图最为接近一致,主要原为试验值曲线图是在El-Centro波(_el)作用下所获得的。而其它地震波形如Taft波(_ta)和人工拟合波(_rg)仅作为补充条件,在同向地震作用时其最大加速度峰值均低于El-Centro波(_el),故对应的地震反应也低于同向的El-Centro波(_el)作用下的试验值,这反映出地震波的不同频谱特性对结构体系的反应影响显著的特点。分析结果表明,楼层层间位移最大值首先出现在2层,导致2层裂缝出现后向上下延伸,使得1-3层相继破坏。

图5 结构模型振型周期的计算结果
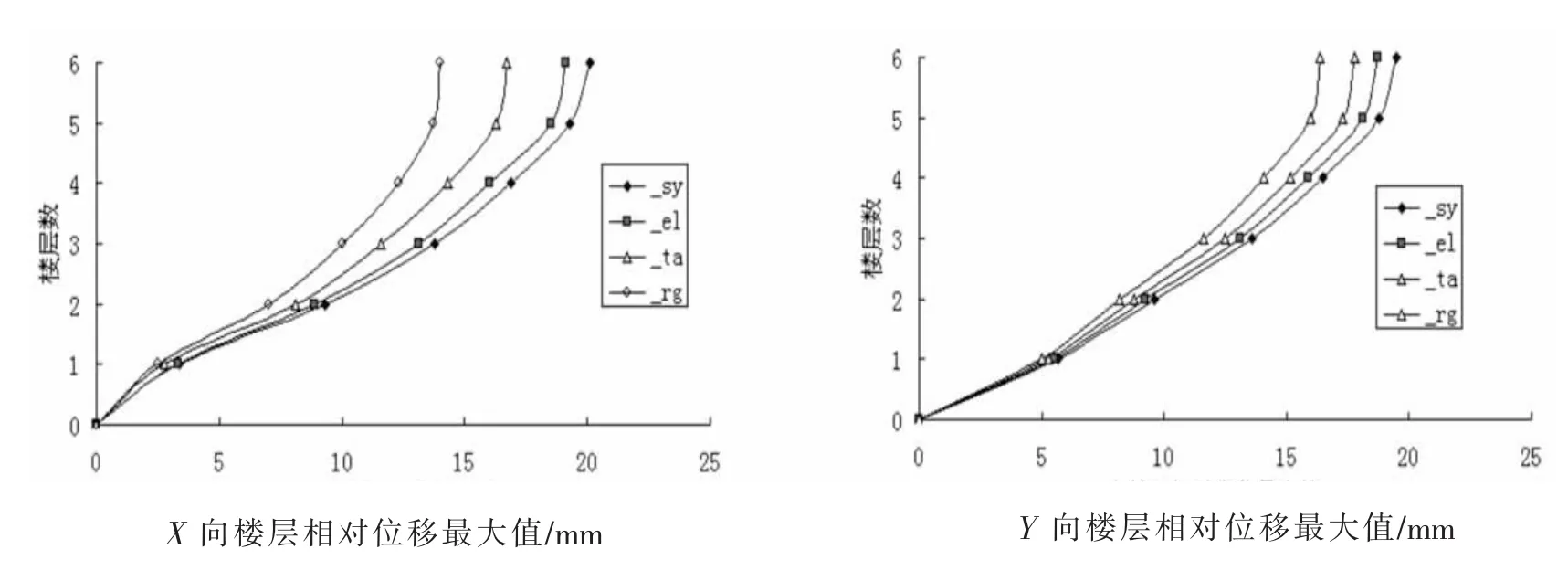
图6 8度(0.2g)多遇烈度时楼层相对位移最大值

图7 8度(0.2g)罕遇烈度时最大相对位移对比值
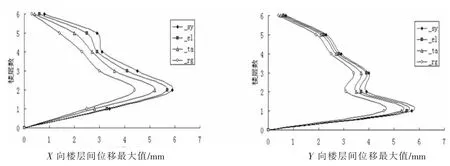
图8 8度(0.2g)多遇烈度时楼层层间位移最大值

图9 8度(0.2g)罕遇烈度时楼层层间位移最大值
表1~2给出了地震波作用下,8度多遇烈度与8度罕遇烈度下,楼层层间位移角最大值对比情况。表1可知,框架结构的楼层位移值在多遇烈度下,除了二层外,其余各层基本满足异形柱框架结构位移限值1/600[9],X波作用下,2层层间角位移超出了限值,也是试验值最先出现破坏的位置,由此分析可知,2层为薄弱层,计算结果与试验结果相接近。在8度罕遇烈度下,结构进入弹塑性阶段,框架结构1层至3层位移均超出了允许限值1/60[9],3层相继进入破坏模式。

表1 地震波作用下结构楼层层间位移角最大值mm
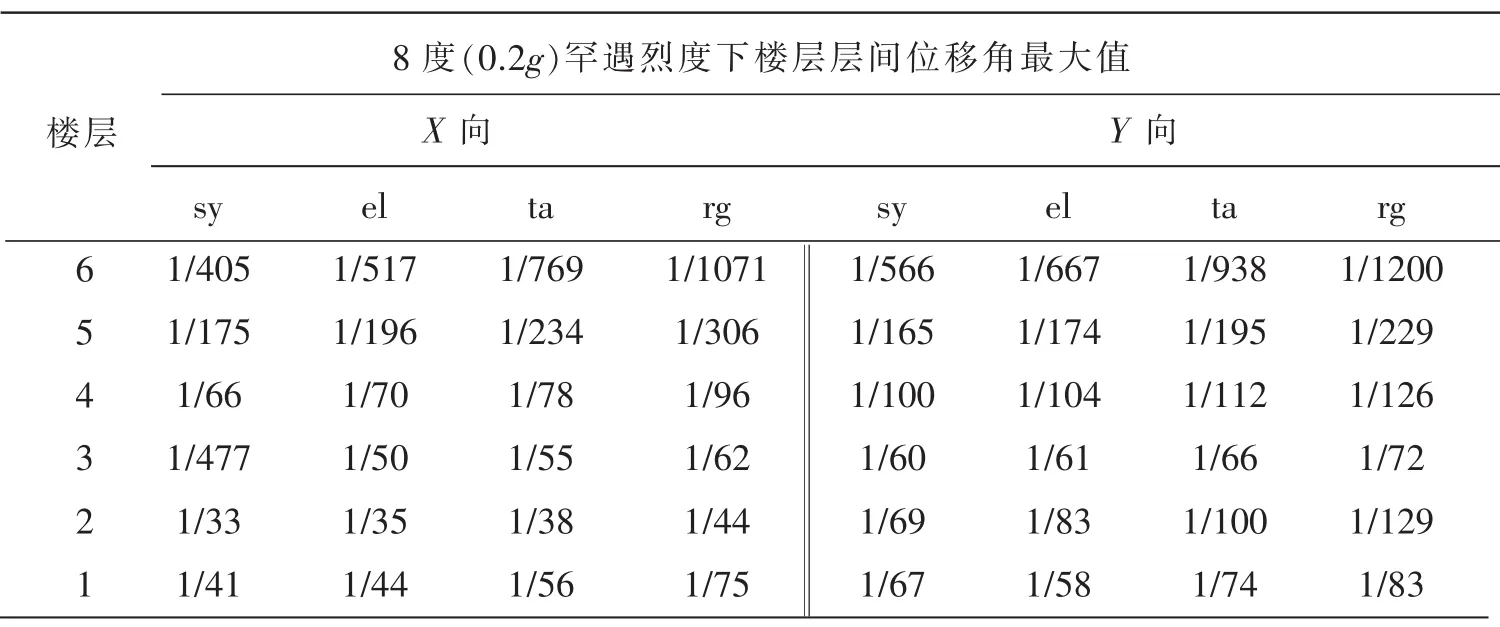
表2 地震波作用下结构楼层层间位移角最大值mm
4 结论
(1)由图3知,在El-Centro波型作用下,异形柱框架结构的试验结果与ANSYS模型的计算结果在低阶振型时较为吻合。低阶振型模态主要表现为整体平动和整体扭转。第一振型主要为整体横向(X向)平动,第二振型主要为整体纵向(Y向)平动,同时还伴随着扭转效应的出现。振型曲线前2阶主要为剪切变形。
(2)由图6~9可知,在8度多遇地震和8度罕遇地震下,由于异形柱框架结构的试验结果是在El-Centro波形作用时获得,所以ANSYS模型在El-Centro波形作用时的计算结果与试验结果最为吻合。而在Taft波(_ta)和人工拟合波(_rg)作用时,ANSYS计算模型的计算值如楼层相对位移反应最大值、层间位移反应最大值仅与试验值走势整体一致。2层及3层出现了较大的层间位移值。三种地震波对结构体系地震反应的差别,也可以反映出地震波的不同频谱特性和持时对结构体系的反应影响显著。
(3)由表1及表2可知,楼层相对位移角最大值也出现在第二层和第三层,即薄弱部位出现在第二层、第三层。所以针对存异形柱框架结构,如何加强薄弱层的设计成为工程设计人员考虑的关键部分。
(4)由上述(1)(2)(3)三部分结论可知,ANSYS模拟异形柱框架结构地震反应具有较强的合理性和可行性,可以弥补振动台实验的不足,其分析结果可为工程人员抗震设计提供设计依据。
参考文献:
[1]王滋军,范明环,刘军,等.混凝土异形柱结构的研究与应用[J].混凝土与水泥制品,2015(10):48-52.
[2]杜玉莹.异形柱在住在住宅结构设计中应注意的相关问题研究[J].建材与装饰,2016(36):75-76
[3]柳阳,刘红兵、任兴民.规则异形柱框架抗震性能分析[J].特种结构,2016(5):104-108.
[4]李自林,丁宏毅、尚军,等.体型不规则异形柱框架结构整体抗震性能分析[J].工业建筑,2014(s1):135-138.
[5]张永强.八度区异形柱结构体系的抗震性能试验研究[D].上海:同济大学,2005.
[6]刘祖强,薛建阳.实腹式型钢混凝土异形柱框架结构受力性能有限元分析[J].工业建筑,2017(4):51-56.
[7]曹万林.异型柱框架结构及构件抗震性能和设计方法的研究[R].河北工业大学,1996.(4):17-26.
[8]中华人民共和国行业标准.混凝土异形柱结构技术规程:GB50011-2010[S].2010.12
[9]中华人民共和国行业标准.混凝土异形柱结构技术规程:JGJ149-2006[S].2006.7
