几类可乘过程及其小偏差估计

傅有明，林莎莎，黄婉君

（三明学院 信息工程学院，福建 三明365004）

乘积随机过程[1]已广泛应用于随机分析及其交叉学科的应用中，其中较为常见的是在时间序列中关于乘积模型的论述[2]，例如，时间序列中通常含有长期趋势（T）、季节变动（S）、循环变动（C）和不规则变动（I）4种成分，统计上对这4种成分的结合方式有两种不同的假设，从而形成加法和乘法两类理论模型。而乘法模型假设时间序列中每一个观测值都是4种成分的乘积，即：Y＝T·C·S·I，4种成分之间保持着相互依存的关系，如要测定某种成份的变动，须从原时间序列中除去其他影响成份的变动，有关更多乘积模型可参见文献[3-5]。

本文主要定义点乘、叉乘和纯积几类乘积过程，利用布朗运动的相关性质分析有关布朗型可乘过程的概率属性，特别地，给出了这几类布朗型可乘过程的小偏差估计。

1 可乘过程的构

1.1 点乘过程

定义 1若Xt=Yt·Zt，则称随机过程{Xt；t∈R+}为过程{Yt；t∈R+}与过程{Zt；t∈R+}的Ⅰ型点乘过程。

定义 2若 Xt=Yt1·Zt2，则称随机过程为过程{Yt1；t1∈R+}与过程{Zt2；t2∈R+}的Ⅱ型点乘过程。

1.2 叉乘过程

定义 3若 Xt=Yt×Zt，则称随机过程{Xt；t∈R+}为过程{Yt；t∈R+}与过程{Zt；t∈R+}的Ⅰ型叉乘过程。

定义 4若 Xt=Yt1×Zt2，则称随机过程为过程{Yt1；t1∈R+}与过程{Zt2；t2∈R+}的Ⅱ型叉乘过程。

1.3 纯积过程

定义 5若，则称随机过程为过程{Yit，t∈R+}，i=1,2，…，n的Ⅰ型纯积过程。

定义 6若，则称随机过程为过程{Yiti，ti∈R+}，i=1,2，…，n的Ⅱ型纯积过程。

根据上述定义1～6，可知Ⅰ型过程为单指标过程，Ⅱ型过程为多指标过程。

2 布朗型可乘过程

在有关各类可乘过程构造的基础上，给出有关布朗型可乘过程的相关概率属性及其小偏差估计。为讨论方便，先给出有关布朗运动的相关概念与性质。

定义[6]：1.1{Bt，t∈R+}称为一个 d 维布朗运动，如果

引理 1[7]设{Bt，t∈R+}为 d维布朗运动，则

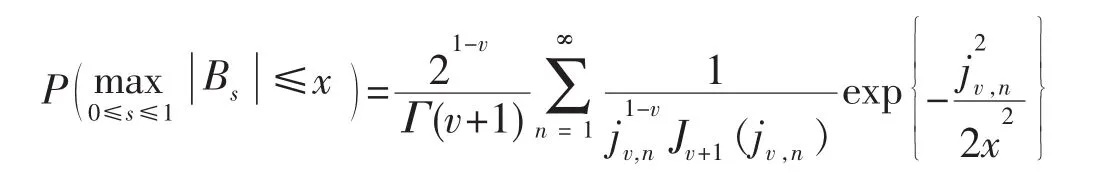
其中 v=（d-2）/2，0＜jv，1＜jv，2是 Bessel函数 jv的正零点。

引理 2[7]设{Bt，t∈R+}为 d维布朗运动，则

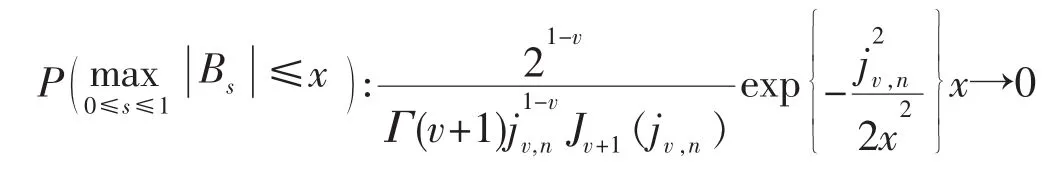
引理 3[7]设{Bt，t∈R+}为 d 维布朗运动，则对任意 x＞0，存在常数 K＞0，有

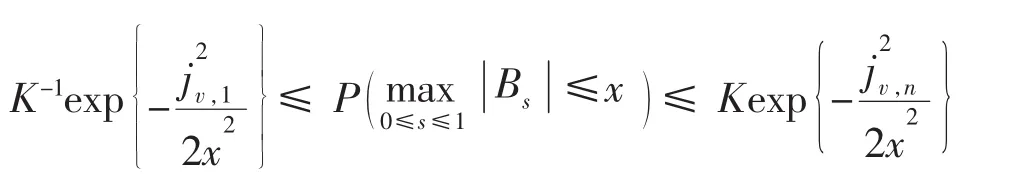
引理 4[8]设{Bt，t∈R+}为一维布朗运动，则

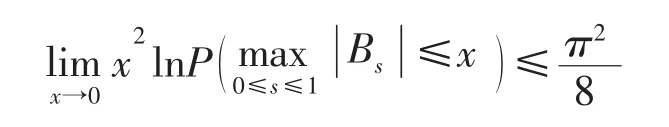
若Xt=Bt·Bt，其中{Bt；t∈R+}为d维布朗运动，即

从而根据χ2分布的性质得Xt=Bt·Bt的概率密度函数为

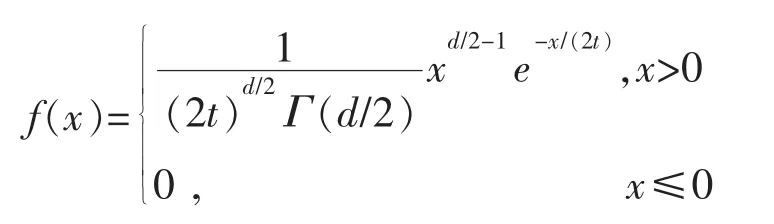
数学期望 E（Xt）=dt，方差 D（Xt）=2dt2。

进一步地，有如下给出关于布朗型可乘过程Xt=Bt·Bt的最大值分布特征。

命题1设Xt=Bt·Bt，其中{Bt；t∈R+}为d维布朗运动，则有

存在常数 K＞0，有

证明：

利用引理 1及（1）式，即有

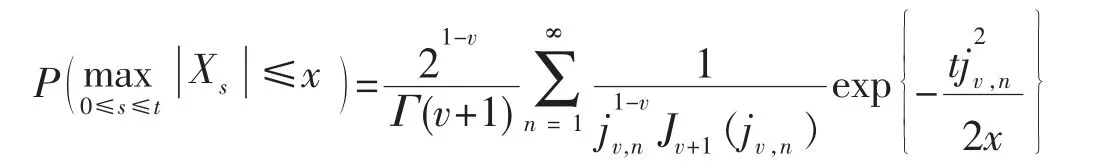
利用引理 2及（1）式，即有

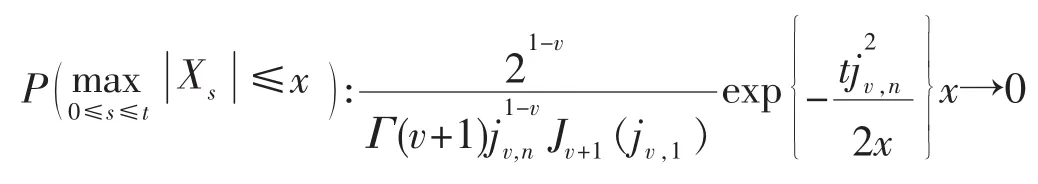
利用引理3及（1）式，即存在常数，有

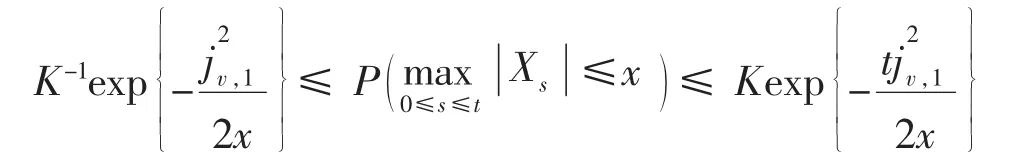
利用上述命题所得的第2个结论即可得到如下有关于布朗型自乘过程Xt=Bt·Bt的小偏差结论。

推论1设Xt=Bt·Bt，其中{Bt；t∈R+}为d维布朗运动，则有

若Xt=B1t·B2t，其中{B1t；t∈R+}与{B2t；t∈R+}为相互独立的d维布朗运动，即

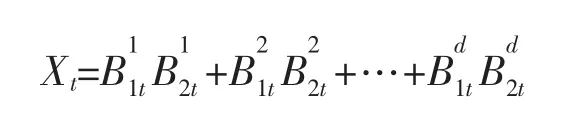
下面的命题给出了布朗型可乘过程Xt=B1t·B2t的小偏差下界估计。

命题2设Xt=B1t·B2t，其中{B1t；t∈R+}与{B2t；t∈R+}为相互独立的d维布朗运动，则有

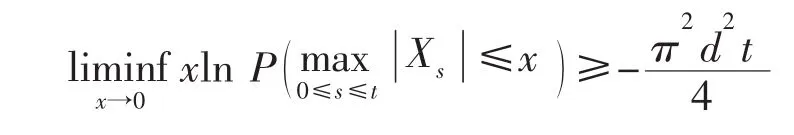
证明：利用Xt=B1t·B2t的构造原理及{B1t；t∈R+}与{B2t；t∈R+}的独立性，有

利用引理 4及（2）式，即有

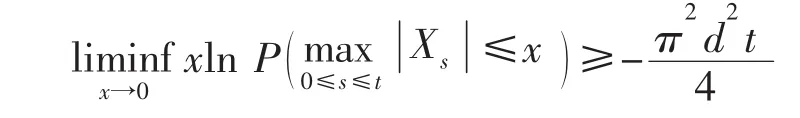
若Xt=B1t·B2t,其中{B1t；t∈R+}与{B2t；t∈R+}为相互独立的d维布朗运动，即

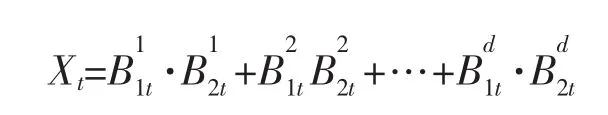
下面的命题给出了布朗型可乘过程Xt=B1t·B2t的小偏差下界估计。

命题 3设 Xt=B1t1·B2t2，{B1t1；t1∈R+}与{B2t2；t2∈R+}为相互独立的 d 维布朗运动，则有

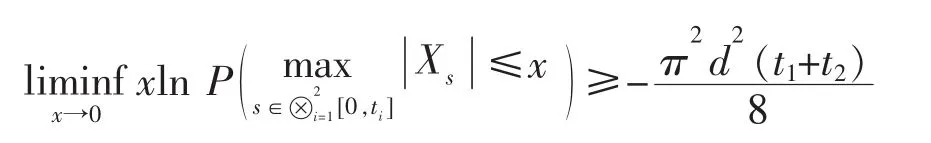
证明：利用Xt=B1t·B2t的构造原理及{B1t；t∈R+}与{B2t；t∈R+}的独立性，有

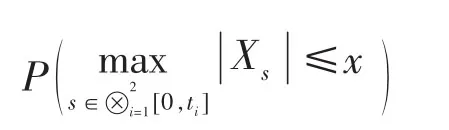
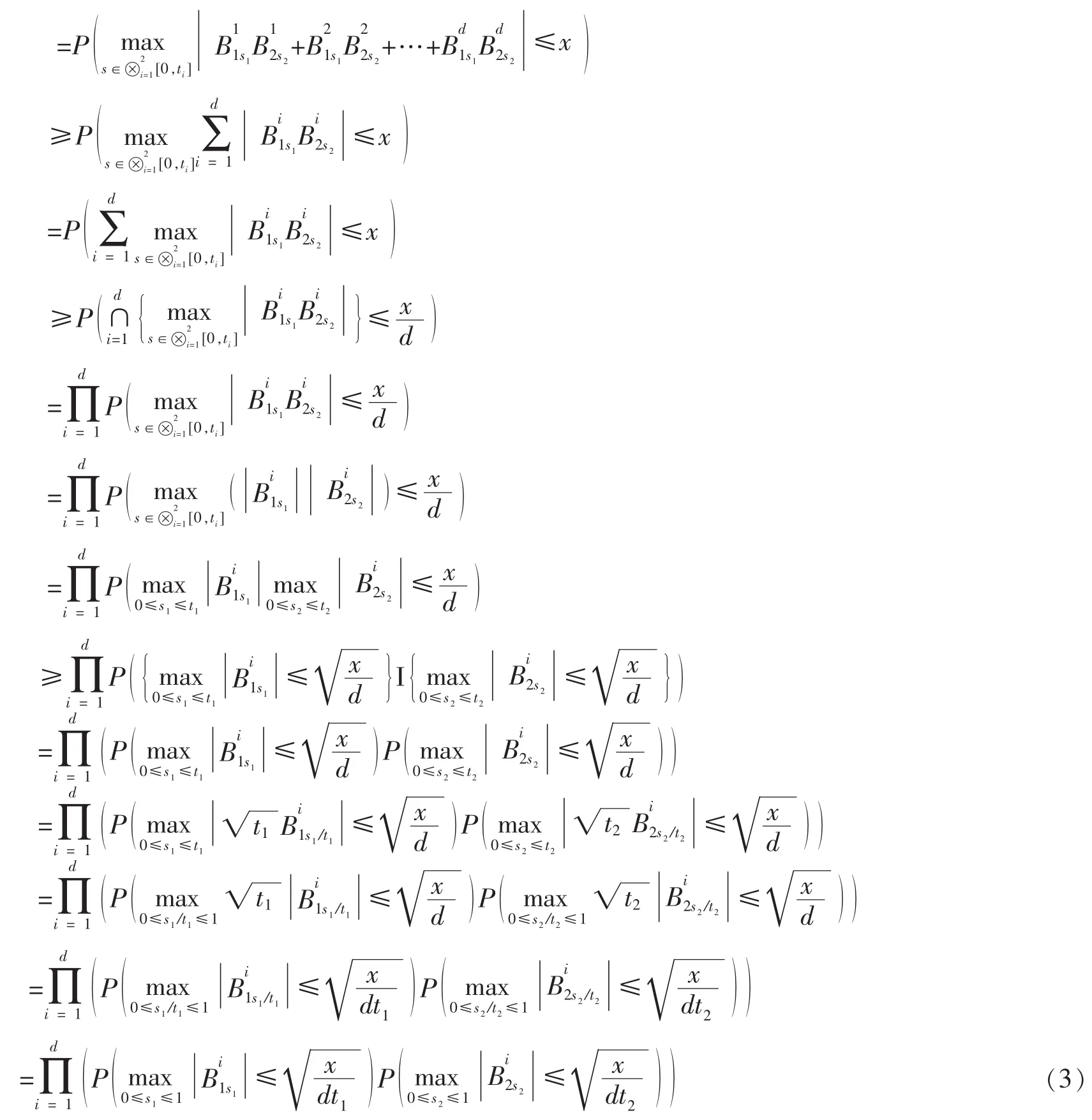
利用引理 4及（3）式，即有

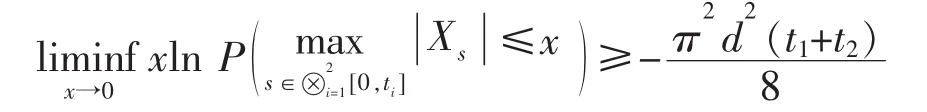
命题4设其中{Bit；t∈R+}，i=1,2，…，n 为相互独立的一维标准布朗运动，则有

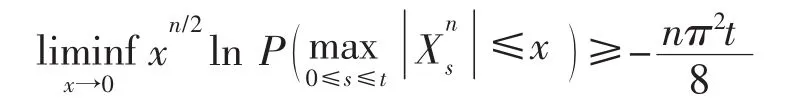
证明：利用的构造原理及{Bit；t∈R+}，i=1,2，…，n 的独立性，有

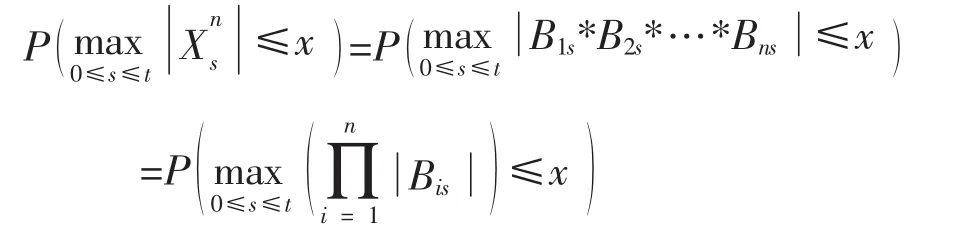
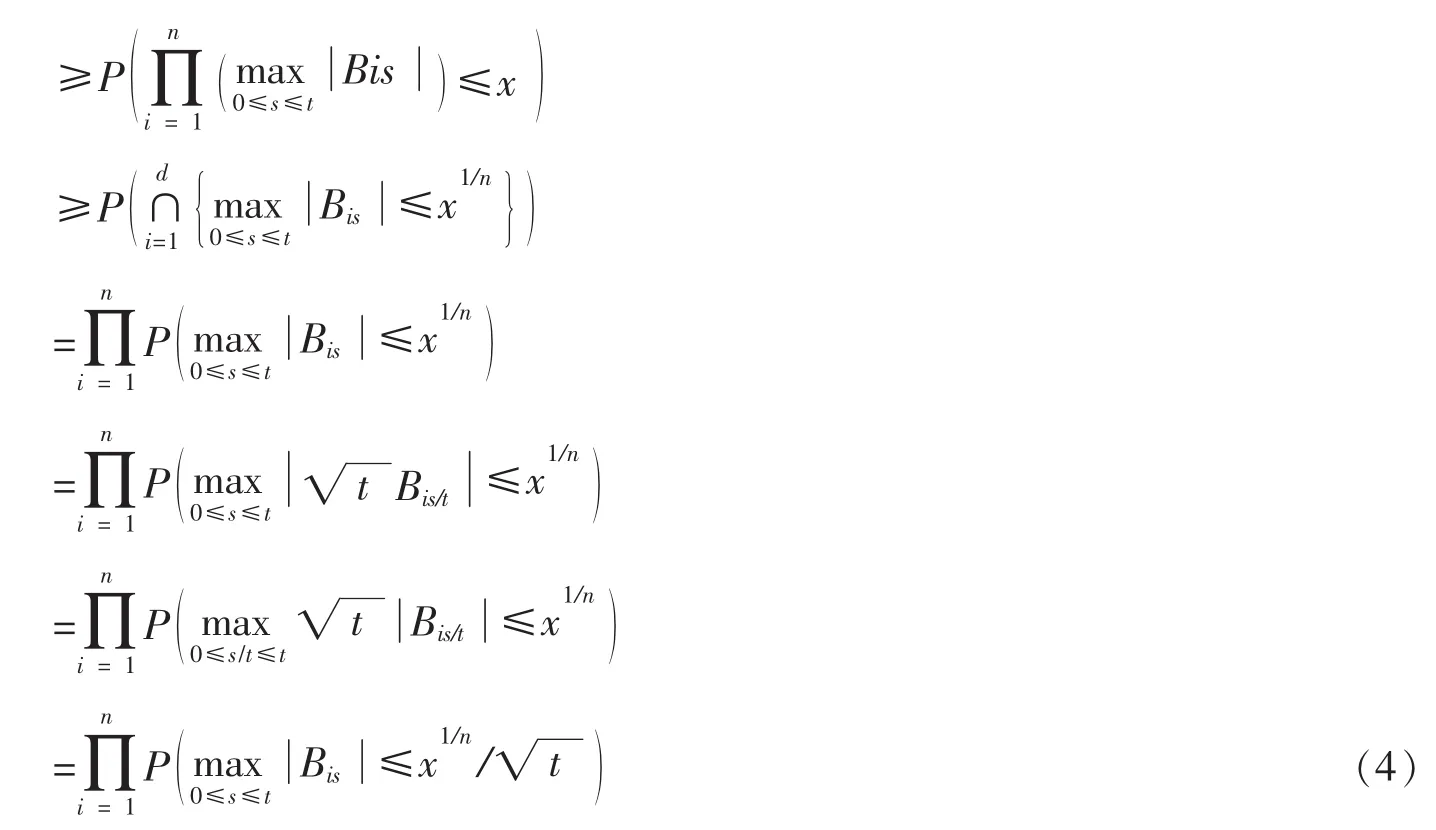
利用引理 4及（4）式，即有

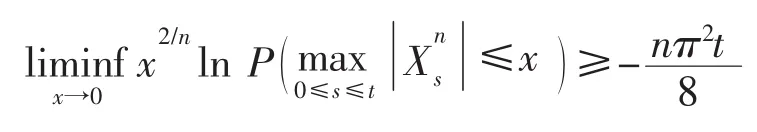
则根据χ2分布的性质得的概率密度函数为

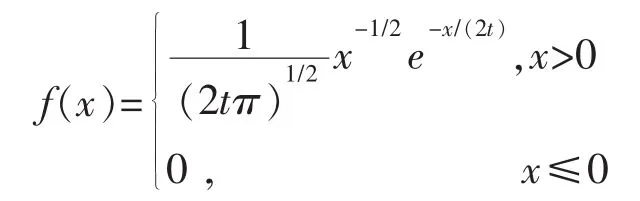
命题5设，其中{Bt；t∈R+}为一维布朗运动，则有

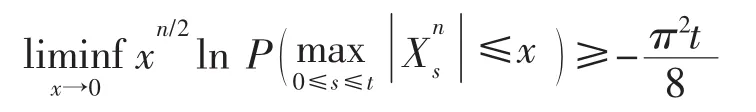
证明：利用的构造原理，有

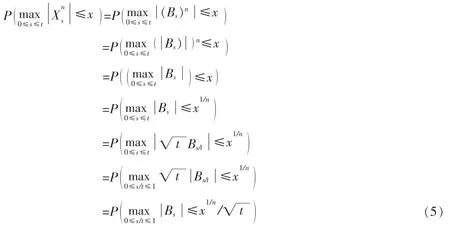
利用引理4及（5）式，即有

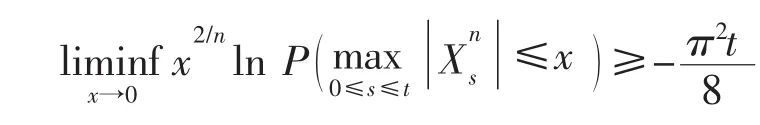
命题6设，其中{Biti；ti∈R+}，i=1,2，…，n 为相互独立的一维标准布朗运动，则有

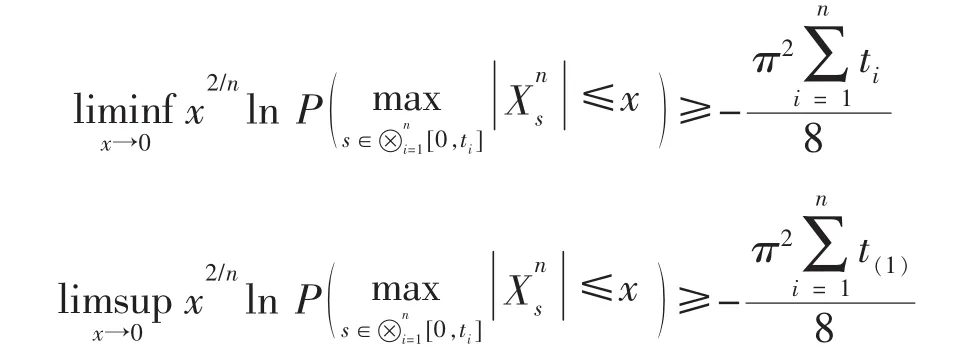
证明：一方面

利用引理 4及（6）式，即有

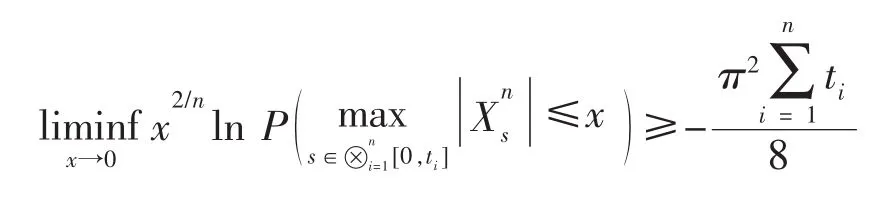
另一方面

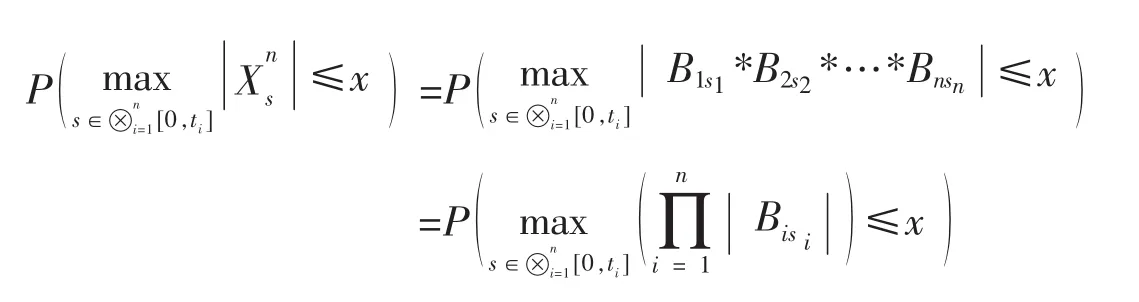
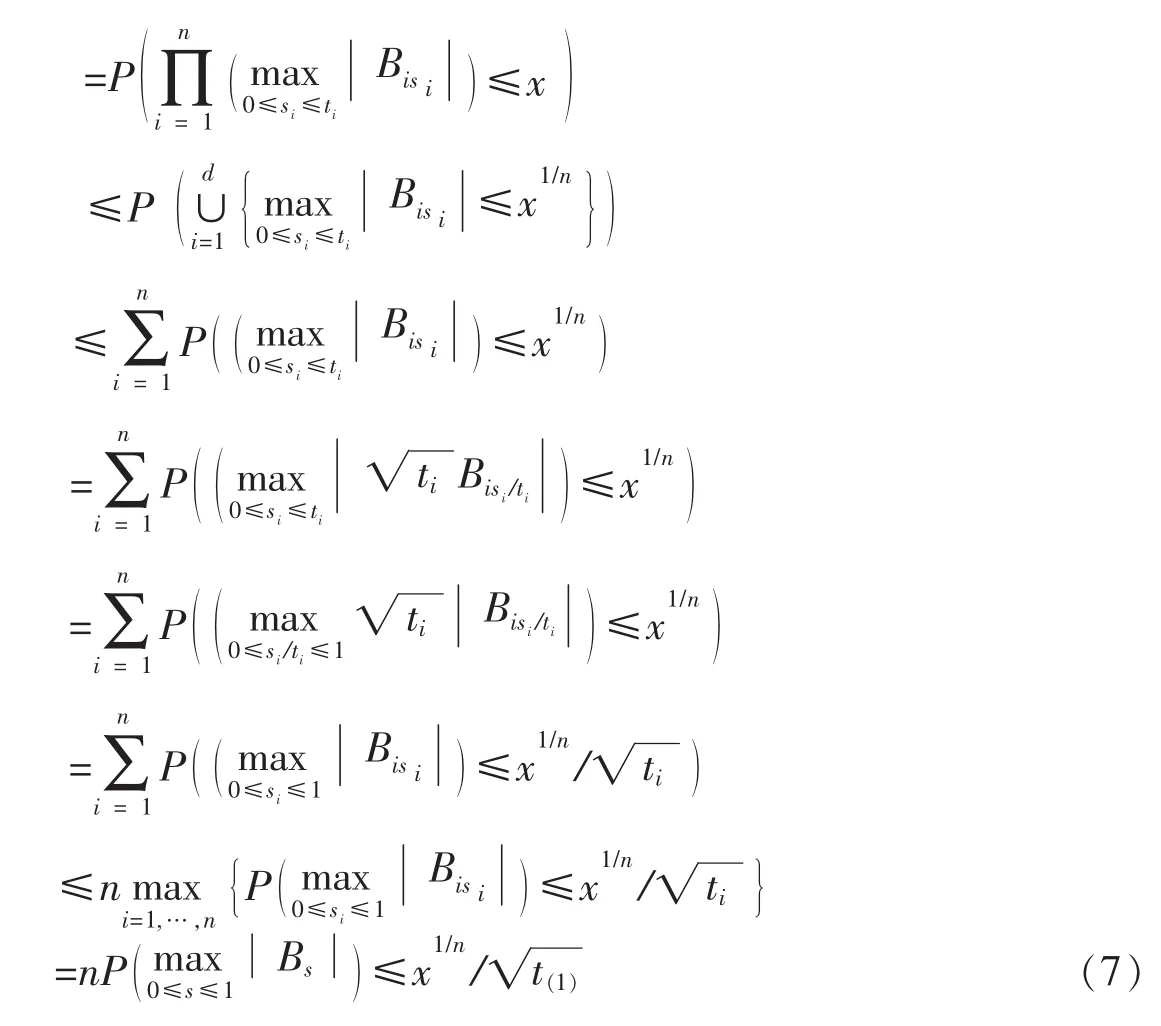
3 结束语

本文只得到了布朗型可乘过程小偏差估计，其小偏差的精确表达有待继续深入探究，且还有值得进一步探讨的布朗型可乘过程，如 Xt=B1t×B2t，其中{B1t：t∈R+}与{B2t：t∈R+}为布朗运动，即

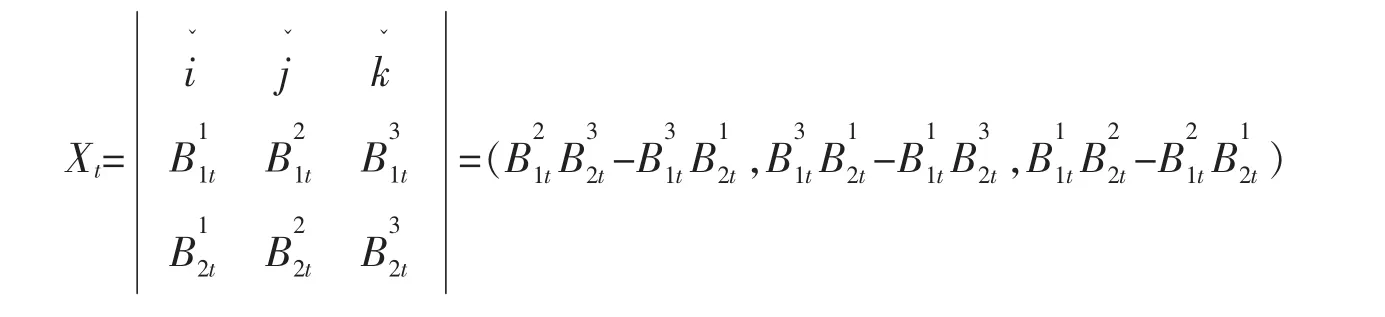
参考文献：

［1］孙荣恒.随机过程及其应用[M].北京：清华大学出版社，2003：40－43.

［2］梁会民.基于熵 AHP 和乘法模型的城市化水平测度［J］.现代城市， 2011（4）：14－17.

［3］蒋庆琅.随机过程原理与生命科学模型［M］.方积乾，译.上海：上海翻译出版公司，1987：132－216.

［4］邱小兰，姚鸣红，马国胜.运用最小平方趋势季节乘法模型预测门诊人数［J］.中国医院统计，2004，11（4）：349－351.

［5］李自勤，王骐，李琦，等.激光成像雷达系统中散斑像的乘法模型及其滤除［J］.中国激光，2003，30（8）：717－720.

［6］钱敏平，龚光鲁.随机过程论［M］.北京：北京大学出版社，2000.

［7］LI W V.The first exit time of a Brownian motion from an unbounded convex domain［J］.Annals of Probability，2003：1078－1096.

［8］CHEN X，LI W V.Small deviation estimates for some additive processes［M］.High Dimensional Probability III.Birkh user Basel，2003：225－238.