基于蒙特卡罗法的道路无控制交叉口通行能力*
2018-05-02周溪召于保坤
周溪召 于保坤
(上海理工大学管理学院1) 上海 200093) (上海海事大学经济管理学院2) 上海 201306)
0 引 言
交叉口通行能力研究对交叉口的规划设计、功能评价等意义重大.与信号控制交叉口和标志控制交叉口相比,关于无控制交叉口的通行能力研究较少.Li等[1]对三个类型的无信号控制交叉口运用公式法进行分析,适用于没有行人和非机动车的混合车流交叉口.Maurya等[2]以混合交通状况下的无控制交叉口为研究对象,根据车型将临界间隙进行分类,分析了不同因素对驾驶员穿越交通流行为选择的影响 .Guler等[3]建立了一种评估无控制交叉口平均延误的方法,结合不同交通流的需求和优先级确定不同方向的通行能力.Prasetijo等[4]指出间隙接受理论是评价无信号交叉口的常用方法,但对于不遵守通行权以及混合交通情况不适用,冲突点法克服了这些缺点.Sangole等[5]使用模糊神经网络算法对无控制交叉口的两轮车通行进行了研究.李爱增等[6-7]采用车队分析法得到了直行组合车流和左转组合车流的通行能力计算公式,采用最小跟车时距理论得到右转车流通行能力计算公式.林栋等[8]提出了新的无信号交叉口通行能力定义,建立了“非冲突最大流”通行能力计算模型.朱芳芳[9]利用无信号交叉口实测数据建立了行人过街间隙选择行为概率与安全间隙之间的数学关系模型.
上述研究大多是基于交叉口车辆运行的车队特征,利用车队分析法进行研究,主要考虑的是公路交叉口,或分析时假设城市道路上非机动车、行人较少,较少考虑非机动车、行人对无信号交叉口通行能力的影响[10-11].基于此,文中考虑到无控制交叉口内部运行的复杂性,运用冲突点法及间隙接受理论,通过蒙特卡罗法仿真对城市道路无控制交叉口通行能力进行较为系统的研究.
1 基本概念
无控制交叉口是指具有相同或基本相同重要地位,从而具有同等通行权的两条相交道路,因其流量较小,在交叉口上不采取任何管理手段的交叉口[12].
冲突点是指来自不同方向的交通流线以较大角度或接近90°角度相互交叉的地点.冲突点处由于交通流线角度很大,发生撞车的可能性最大,对交通干扰影响很大.冲突点主要产生在交叉口相交的公共区内,左转、直行交通流线之间[13].
蒙特卡罗法是一种与一般数值计算方法有本质区别的计算方法,属于试验数学的一个分支,起源于早期的用几率近似概率的数学思想,它利用随机数进行统计试验,以求得的统计特征值作为待解问题的数值解.利用各种不同分布随机变量的抽样序列仿真实际系统的概率模型,给出问题数值解的渐近统计估计值[14].
随机数表法是事先人为地产生一批均匀随机数,并制成表格形式备用.当需要使用它时,直接调用这张随机数表就可以了.随机数表中,每个数在表中某个位置出现的概率完全相同,这些数就是随机顺序排列的.当实际使用时,可以随机地从表中任何地方开始顺序地读取[15].
临界间隙是指交叉口主路车流允许支路等待穿越车辆通过的最小间隙.因此,临界间隙是指在主要车流中出现的驾驶员能够接受的最小间隙.一般情况下,驾驶员会拒绝一些小于临界间隙的时间间隔而接受一个大于临界间隙的时间间隔.
随车时距是指支路排队车辆连续通过交叉口时相邻两车之间的时间间隔,即支路车流在无其他车辆冲突影响下以饱和车流通过交叉口的车头时距.
2 基本公式及方法
2.1 基本公式
2.1.1行人群到达时距的移位负指数分布
研究表明,当行人流量≤4 000人/h时,行人群的到达时距hp可用移位负指数分布来拟合:P(h>t)=exp[-(t-1)/(Hp-1)],即
P(hp≤t)=1-exp[(t-tpp)/(Hp-tpp)] (1)
式中:hp为行人群与群之间的到达时距,s;Hp为每群行人在行人流量为p时的平均到达时距,s;tpp为划分行人群的最小空隙值,s.
2.1.2机动车到达车头时距的移位负指数分布
移位负指数分布是负指数分布的改进,它将负指数分布曲线从原点沿时间轴向右移动一个最小间隔长度tp,移位负指数分布的分布函数为
(2)
式中:θ为尺度参数;tp为最小车头时距,s.
2.1.3机动车到达车头时距的M3分布
假设交通流由自由流和跟随状态车流两部分组成,当车流以跟随状态或车队状态行驶时,车头时距为常数tp,当车流以自由流状态行驶时其车头时距服从移位负指数分布,以参数Ø来表示自由流的比例.M3分布的分布函数为
(3)
式中:γ为衰减常量;Ø为自由车流比例;tp为最小车头时距,s.
2.2 方法步骤
2.2.1随机数表制作
本文所用随机数表均由EXCEL生成,编辑表格Randbetween(1,100),表格中数字在1~100中随机产生,由此制成多个随机数表,由于每次打开表格数字都是随机出现,故任意选取一次打开结果,新建表格复制数字.
2.2.2冲突点分析及简化
选择观察方向,以观察方向机动车流A为研究对象,绘制交叉口交通流流向及冲突流示意图,见图1.在冲突点较多的情况下,同一个进口道进入路口的直行和左转车流先不分流,统一为直行车流考虑.

图1 冲突示意图
2.2.3各冲突方向参数表制作
假设冲突方向有机动车流D.D的到达时距服从分布函数FD(t).设A车流车辆穿越机动车流D的随车时距为tf,临界间隙为tc.机动车流D通过交叉口的到达时距为tD,则当tc 表1 A车流穿越机动车流D的参数对应表 同理可计算出各个冲突方向的参数对应表. 2.2.4车辆通过交叉口仿真 2.2.5数据处理 优越路-劳动路交叉口位于平顶山市区中心的繁华商业区,由东西方向的优越路和南北方向的劳动路相交而成.两相交道路均为一块板道路,双向2车道.该交叉口四个进口道均为直左右共用车道,北进口距上游信号交叉口的距离为270 m,其他进口的相邻交叉口均为无信号交叉口. 研究表明,交叉口到达交通量小于500 veh/h时,用移位负指数分布描述车头时距符合实际情况;与上游交叉口距离在400 m以内时,车辆的到达车头时距服从M3分布. 故北进口的车头时距分布用M3分布进行描述,其他进口的车头时距分布用移位负指数分布进行描述.另外,由上文知,该交叉口4个进口的当量人群流的群时距用移位负指数分布进行描述.以下计算以南进口车道为例. 右转机动车穿越当量人群流的临界间隙为3.27 s,随车时距为2.48 s.相应的时间分段、对应概率、随机数范围及可通过车辆数见表2~3. 表2 右转车流穿越东西向行人流的参数对应表 表3 右转车流穿越南北向行人流的参数对应表 右转车流穿越两个相邻冲突点时,时间是连续进行的,因而需要同时选取两个随机数进行仿真.东西向和南北向当量人群流的到达时距数据分别由随机数一和随机数二查相应参数表获得,即表4中间时刻一和中间时刻二. 表4 右转车流通过交叉口仿真过程部分数据表 南进口直行车辆共有6个冲突点,依次是东西向行人流(近交叉口南进口处)、东进口左转机动车流、西进口直行机动车流、东进口直行机动车流、北进口左转机动车流、东西向行人流(近交叉口北进口处).由于冲突点过多,东进口左转机动车与直行机动车暂不分流,统一为直行车流.简化后有5个冲突点,直行车流穿越5个冲突点时间是连续进行的,因而需要同时选取5个随机数进行仿真. 南进口左转共有6个冲突点,依次是:东西向行人流(近交叉口南进口处)、西进口直行机动车流、东进口左转机动车流、西进口左转机动车流、北进口直行机动车流、东西向行人流(近交叉口北进口处).由于冲突点过多,西进口左转机动车与直行机动车统一为直行车流考虑.简化后有5个冲突点.左转车流穿越5个冲突点时间是连续进行的,因而需要同时选取5个随机数进行仿真. 运用蒙特卡罗法对无控制交叉口通行能力测算模型进行仿真,由于交叉口的差异性和实际通行的复杂性,文中的参数也会发生变化.因此,测算数据仅代表该路口通行能力,要使该计算模型更有参考性,还需考虑更多的影响因素,对更多的交叉口进行调查和仿真应用. 仿真结果表明,可以用蒙特卡罗法进行仿真计算出无控制交叉口的直行、左转和右转车道的通行能力.仿真过程接近现实情况,在机理上更清晰,更具有可解释性,克服了公式计算通行能力的抽象性.由于仿真过程中忽略车辆的启动损失时间、非观察方向相互冲突以及共用车道不同转向车辆间影响等因素,该计算方法还有待进一步的完善. [1] LI H, DENG W, TIAN Z, et al. Capacities of unsignalized intersections under mixed vehicular and nonmotorized traffic conditions[J]. Transportation Research Record Journal of the Transportation Research Board,2009,21(1):129-137. [2] MAURYA A K, AMIN H J, KUMAR A. Estimation of critical gap for through movement at four leg uncontrolled intersection[J]. Transportation Research Procedia,2016,17:203-212. [3] GULER S I, MENENDEZ M. Methodology for estimating capacity and vehicle delays at unsignalized multimodal intersections[J]. International Journal of Transportation Science & Technology,2017(1):55-58. [4] PRASETIJO J, AHMAD H. Capacity analysis of unsignalized intersection under mixed traffic conditions[J]. Procedia-Social and Behavioral Sciences,2012,43(1):135-147. [5] SANGOLE J P, PATIL G R, PATARE P S. Modelling gap acceptance behavior of two-wheelers at uncontrolled intersection using neuro-fuzzy[J]. Procedia-Social and Behavioral Sciences,2011,20(6):927-941. [6] 李爱增.城市道路交叉口空间布局及其通行能力研究[D].南京:东南大学,2008. [7] 李爱增,宋向红.城市无控制交叉口通行能力计算方法[J].交通运输系统工程与信息,2014,14(1):200-208. [8] 林栋,杨孝宽,万悠扬.等权无信号控制交叉口通行能力研究[J].公路交通科技(应用技术版),2014(2):191-194. [9] 朱芳芳.无信号控制交叉口行人过街间隙选择模型研究[J].交通信息与安全,2011, 9(2):36-39. [10] 吴江玲,张生瑞,王秋平,等.信号交叉口行人步行速度特性分析[J].武汉理工大学学报(交通科学与工程版),2014,38(6):1295-1299. [11] 刘金广,于泉,荣建,等.信号交叉口行人自行车交通强度状态划分研究[J].武汉理工大学学报(交通科学与工程版),2009,33(5):932-935. [12] 吴兵,李晔.交通管理与控制[M].北京:人民交通出版社股份有限公司,2015. [13] 杨建明.道路交叉设计[M].北京:中国建筑工业出版社,2013. [14] 齐欢.系统建模与仿真[M].北京:清华大学出版社,2013. [15] 白思俊.系统工程[M].北京:电子工业出版社,2013.
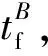




3 案例分析
3.1 无控制交叉口右转车道的通行能力




3.2 无控制交叉口直行车道的通行能力
3.3 无控制交叉口左转车道的通行能力
3.4 无控制交叉口南进口车道的通行能力

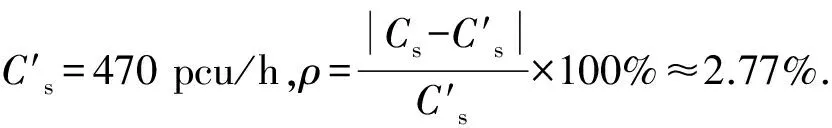
4 结 束 语
