基于变分模态分解和鲁棒性独立成分分析的内燃机缸盖振动信号分离

姚家驰 向 阳 钱思冲 张冠军

1.武汉理工大学能源与动力工程学院，武汉，4300632.武汉理工大学船舶动力系统运用技术交通行业重点实验室，武汉，430063

0 引言

内燃机的缸盖振动信号中蕴含着内燃机工作状态的重要信息，对其进行研究可以判断内燃机的燃烧异常、气门间隙异常、活塞敲击异常等故障[1-4]，因此一直是学者们研究的热点。内燃机缸盖振动信号由许多激励源产生的信号混叠而成，利用时频分析方法不能很好地区分各独立源信号[5]。近年来，盲源分离方法广泛地应用于生物医学信号处理、语音分离、图像处理等领域，许多学者用盲源分离方法对内燃机振动信号进行分离。LIU等[6-7]用盲最小均方差算法从机体振动信号中分离出燃烧信号和活塞敲击信号。康斌等[8]基于Fixed-point ICA算法从缸盖振动信号中分离出燃烧压力激励信号和气门落座激励信号。韩春杨等[9]用多通道盲最小均方差与缩减盲源方法从内燃机表面混合振动信号中分离出燃烧信号和活塞撞击缸体信号。但盲源分离方法要求观测信号数目与源信号数目相同，需要测量内燃机多个通道的振动信号，在实际工程测试中受造价和安装条件的限制，往往只能使用较少的传感器且难以确定源信号的数目，该方法在实际工程应用中受到限制。后来，又有学者提出了内燃机振动信号的单通道分离方法。DU等[10]利用经验模态分解和独立分量分析相结合的方法从内燃机单通道机体振动信号中分离识别出燃烧信号和活塞敲击信号，但是经验模态分解方法缺乏严密的数学推导，产生的端点效应和模态混叠问题会严重影响振动信号的分离效果[11-13]。目前，在缸盖振动信号中，燃烧信号成分和活塞敲击信号成分都发生在上止点附近，在时域和频域上混叠严重，对其进行分离和识别一直是研究的热点和难点。

针对这些问题，本文提出采用变分模态分解(variational mode decomposition, VMD)和鲁棒性独立成分分析(robust independent component analysis， RobustICA)相结合的方法从单通道缸盖振动信号中分离出燃烧信号成分和活塞敲击信号成分，并通过对内燃机不同试验工况下的单通道缸盖振动信号进行分离和识别，验证该方法的有效性。

1 VMD和RobustICA算法的基本原理

1.1 VMD基本原理

变分模态分解算法[14]是一种信号分解算法，采用非递归的分解模式，能够很好地对多分量信号进行分解。假设将一个信号通过变分模态分解算法分解为K个变分模态分量，则其相应的约束变分问题为

(1)

{uk}={u1,u2,…,uK}

{ωk}={ω1,ω2,…,ωK}

在对该约束变分问题进行求解时，需要引入二次惩罚因子α和拉格朗日乘法算子λ将其转变为无约束问题，扩展的拉格朗日表达式：

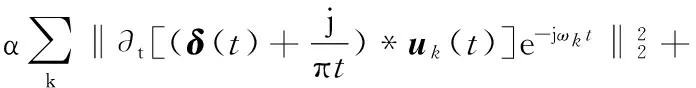
(2)

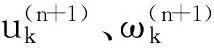
(2)n←n+1；

(3)对k=1,2,…,K，执行

(3)

(4)

(5)

式中，τ为噪声容限参数。

(4)判断是否满足收敛条件：

(6)

式中，c为预先设置的迭代停止值。

若满足条件，则停止程序运行；否则继续执行步骤(2)。

式(3)可写为

(7)

采用Parseval/Plancherel傅里叶等距变换将式(7)变换到频域进行求解：

(8)

对其进行求解后可得到

(9)

同理，可以将式(4)等价为

(10)

对其进行求解后可得

(11)

1.2 RobustICA基本原理

独立分量分析算法的实质是在假设源信号统计独立的基础上，在不知道源信号及混合矩阵任何信息的情况下，试图将一组随机变量表示成统计独立的变量的线性组合。

设X(t)是一组由若干隐含变量产生的p维观测信号，其中i=1,2,…,p表示观测信号的序数，独立分量分析要从p维观测信号X(t)中找出隐含在其中的变量Y(t)，通常为解决多变量数据分析问题，将其简化为一个线性问题进行处理，即

(12)

i=1,2,…,pj=1,2,…,m

写成矩阵形式为Y=WX，即

FastICA算法是应用比较广泛的一种独立分量分析算法[15]，随后ZARZOSO等[16]学者提出了鲁棒性更好和收敛速度更快的RobustICA算法，RobustICA算法是一种基于峭度和最优步长的迭代算法，将一组信号经过RobustICA算法处理后，可以得到各个相互独立的信号成分。

1.3 VMD-RobustICA方法的计算流程

本文提出的VMD-RobustICA方法可从单通道混合信号中恢复出各独立源信号，其计算流程如图1所示。首先用VMD算法对采集的单通道信号进行分解，然后将分解得到的各个窄带模态分量和采集的单通道信号组成一个新的信号组，然后用RobustICA算法对其进行解耦，并用组合模态函数法(combined mode function，CMF)对解耦得到的在时域和频域上相似性较高的分量进行组合[17]，最后结合频谱分析、连续小波变换(continuous wavelet transform，CWT)、相干函数法及倒拖试验对得到的各独立源信号进行识别，其中相干函数定义为

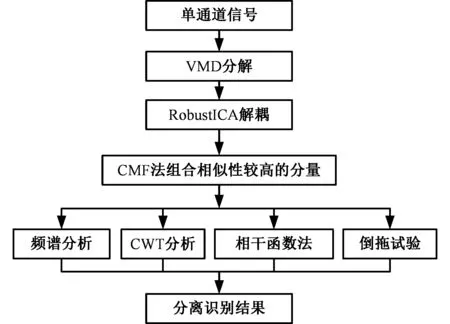
图1 VMD-RobustICA方法的计算流程Fig.1 The calculation process of VMD-RobustICA method

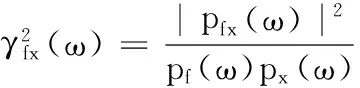
(13)

式中，pf(ω)和px(ω)分别为输入函数f(t)和输出函数x(t)的自功率谱密度；pfx(ω)为输入输出函数的互功率谱密度，相干函数值在0～1之间。

2 内燃机试验

试验对象为WP10-240国Ⅲ型六缸四冲程水冷直列式内燃机，点火顺序为1-5-3-6-2-4。试验台架由WP10-240型内燃机、德国Siemens 1PL6交流电机、倒拖控制台及其控制配件等组成。在试验过程中，以WP10-240型内燃机第6号缸为研究对象，用LC0158T型加速度传感器测量内燃机缸盖的单通道振动信号，用缸压传感器Kistler7013C和单通道电荷放大器5018A1000采集内燃机的缸压信号，用SM-12-100型磁电式传感器采集上止点信号，在进行倒拖试验时，将加速度传感器布置在第6号缸活塞敲击处，测量活塞敲击振动信号，试验测量系统如图2所示，试验工况如表1所示。

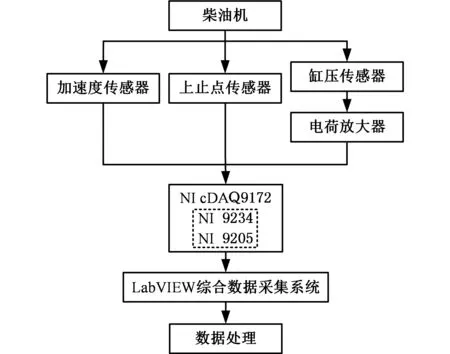
图2 试验测量系统Fig.2 Test measurement system

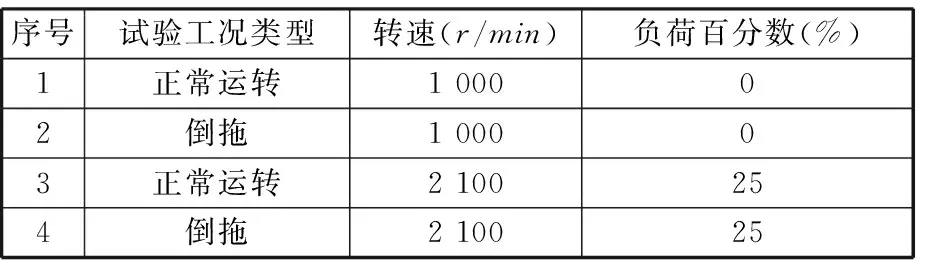
序号试验工况类型转速(r/min)负荷百分数(%)1正常运转100002倒拖100003正常运转2100254倒拖210025

3 缸盖振动信号的分离与识别

在低转速工况下，内燃机的各振动激励源信号相对容易被分离，在高转速高负荷工况下，内燃机的各振动激励源信号中会包含有更多其他干扰成分。本文首先采用VMD-RobustICA方法对内燃机在1 000 r/min空载工况下的缸盖振动信号进行分离和识别，然后对内燃机在额定转速高转速2 100 r/min、25%负荷工况下的缸盖振动信号进行分离和识别。

3.1 内燃机在1 000 r/min空载工况下缸盖振动信号的分离与识别

内燃机试验工况为1 000 r/min空载，采样频率为25.6 kHz，通过试验测得内燃机一个工作循环的缸压pc和缸盖振动加速度信号a如图3所示。

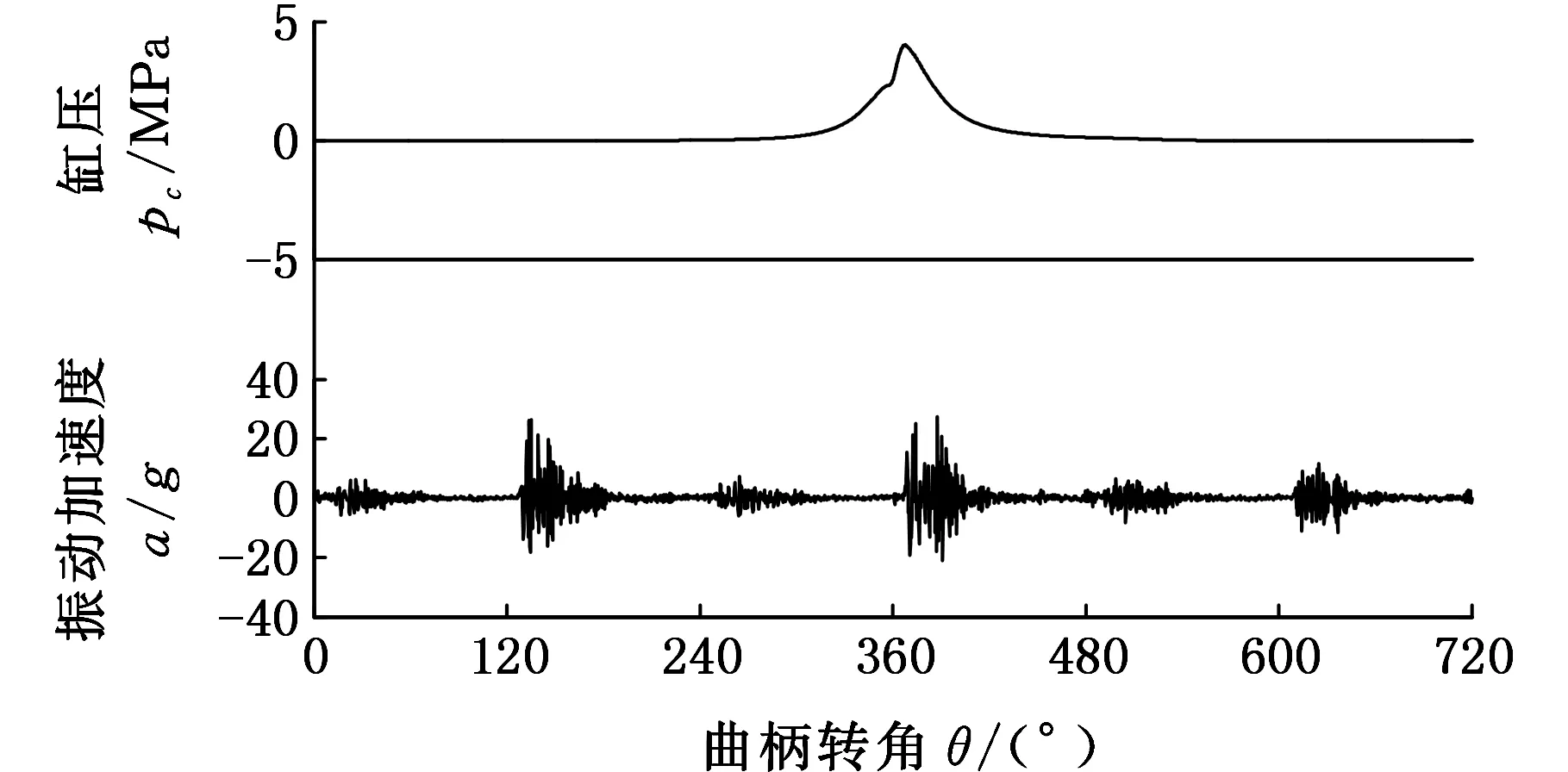
图3 一个工作循环的缸压和缸盖振动信号Fig.3 A working cycle of cylinder pressure and cylinder head vibration signals

为了更好地对缸盖振动信号进行分离，减少在测量信号的过程中产生的随机误差成分，需要对采集的缸盖振动信号进行消除趋势项及滑动平均等预处理，经过预处理后的信号如图4所示。

首先对预处理后的单通道缸盖振动信号进行变分模态分解，在进行变分模态分解之前，需要通过观察对比各个模态的中心频率来确定最佳的模态数K值，通过计算得到的结果如表2所示。

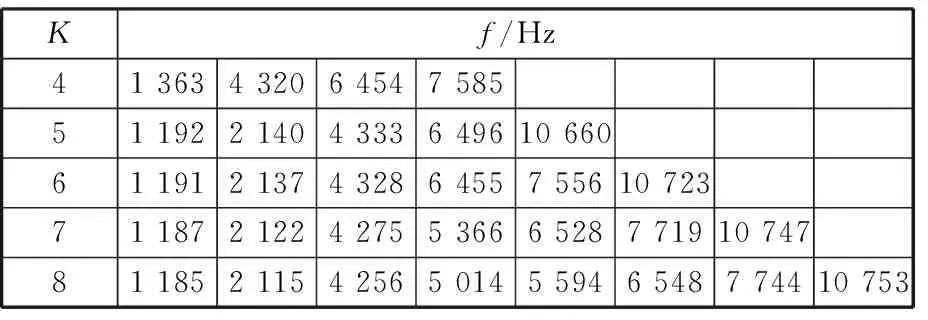
表2 模态数K和中心频率f

从表2中可看出，当模态数K取8时，有两个变分模态分量的中心频率分别为5 014 Hz和5 594 Hz，相距较近，因此可认为出现了过分解，故最佳模态数K应取7。

将预处理后的缸盖振动信号经过变分模态分解处理后可得到7个变分模态分量，由于得到的7个变分模态分量之间不总是相互独立的，因此需要进一步地采用RobustICA算法提取其独立成分。将这7个变分模态分量和预处理后的缸盖振动信号组成一个新的信号组，用RobustICA算法提取独立成分，通过计算得到的结果如图5所示。

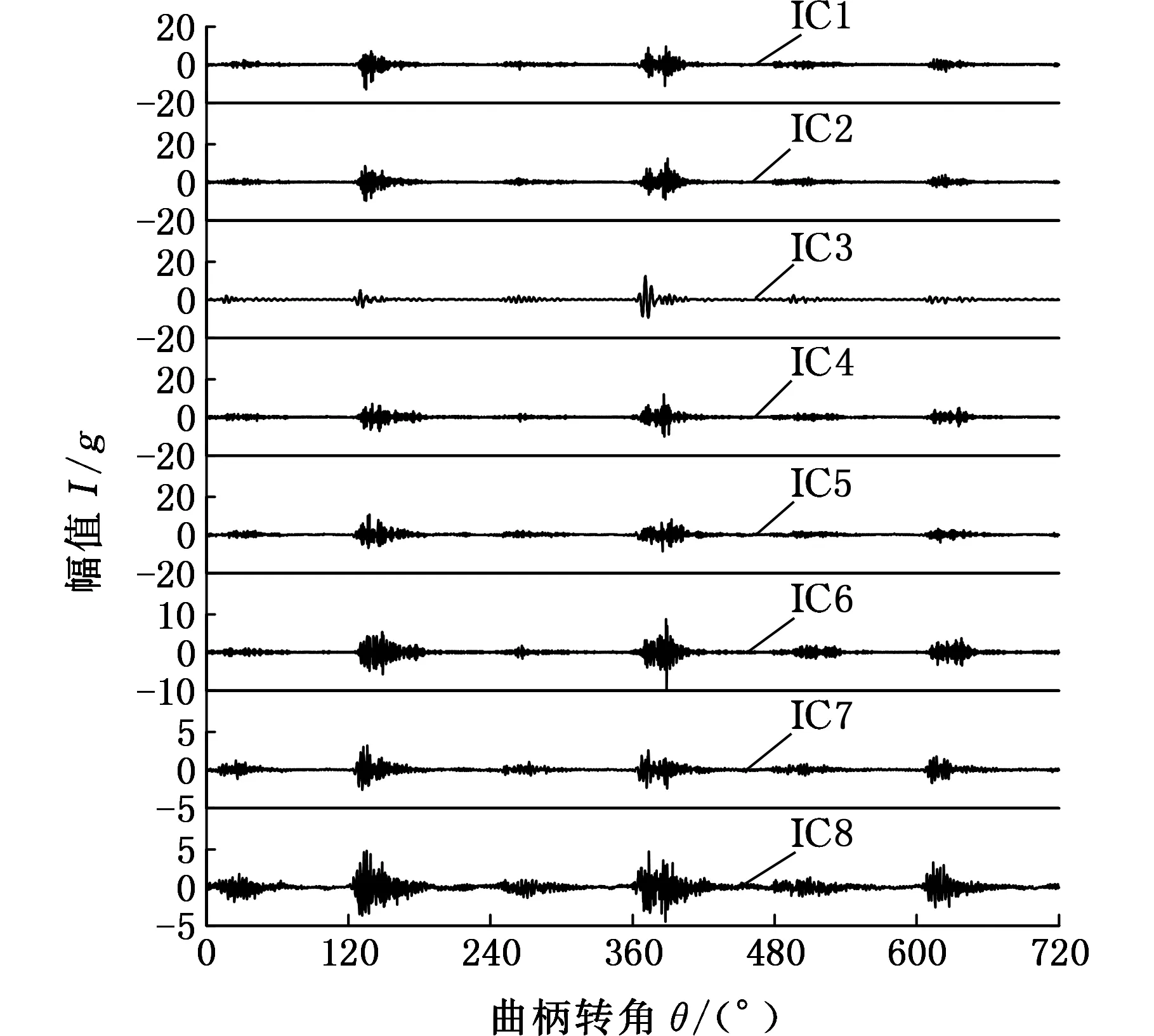
图5 RobustICA计算结果Fig.5 The calculation results of RobustICA

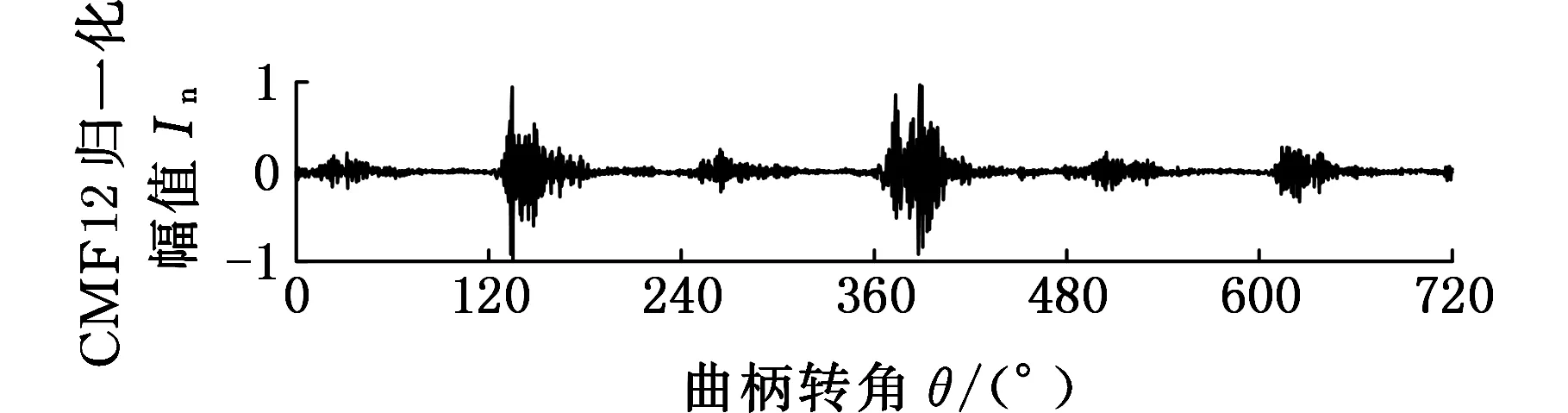
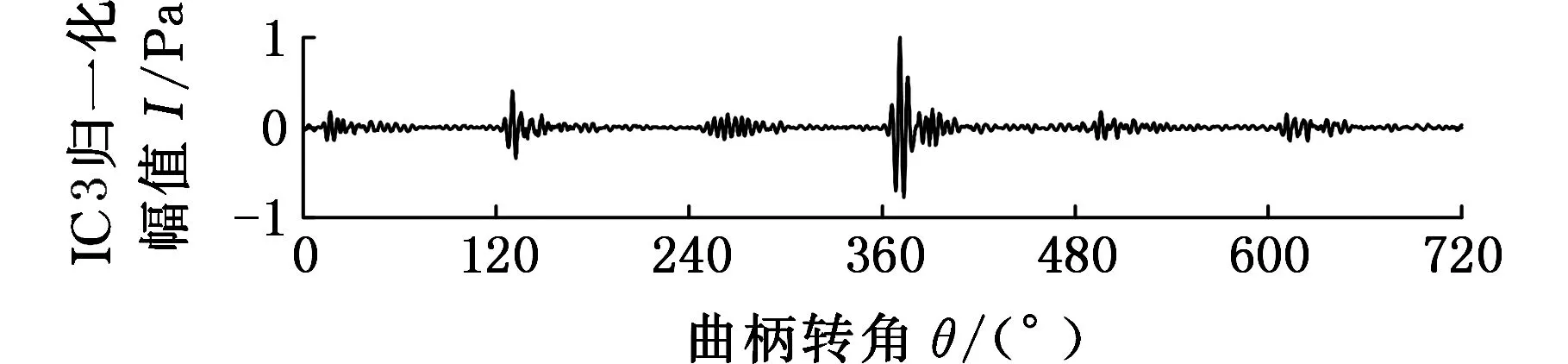
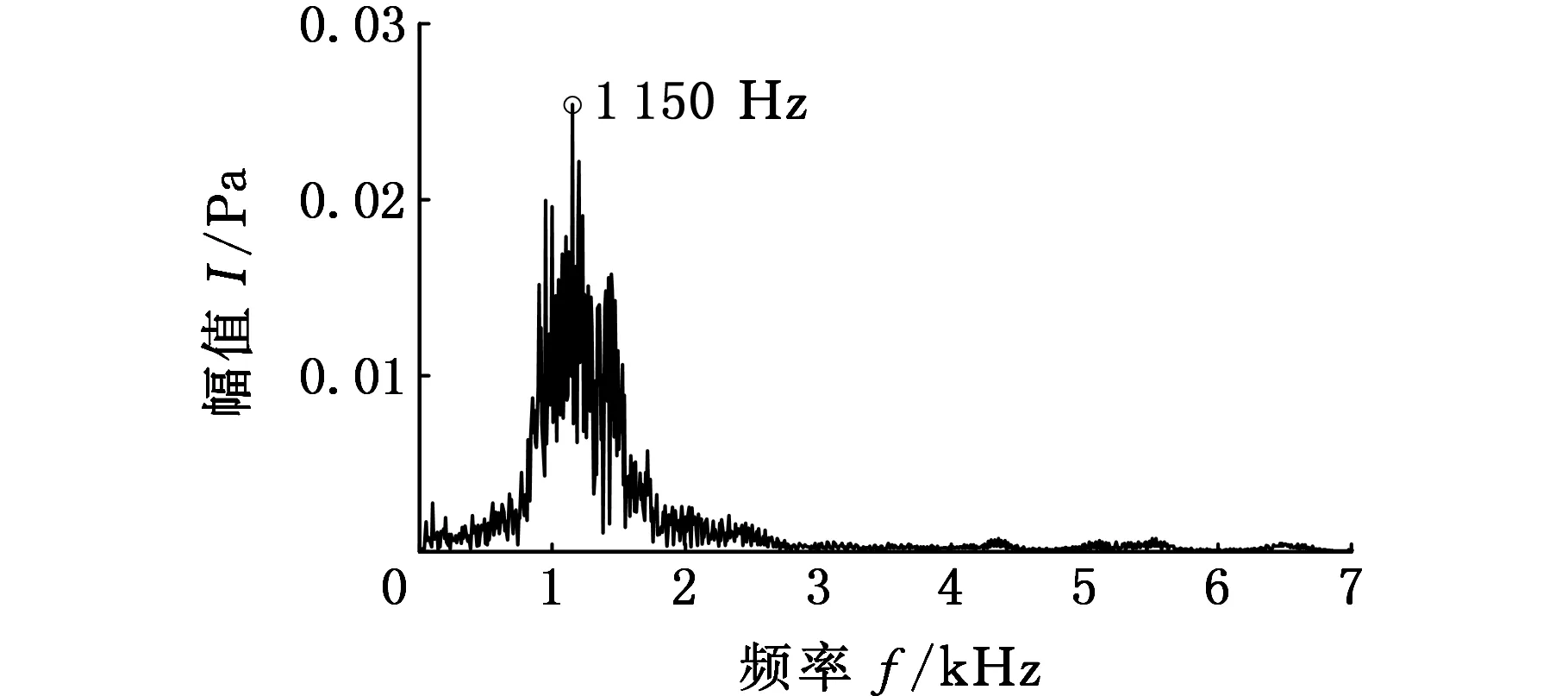
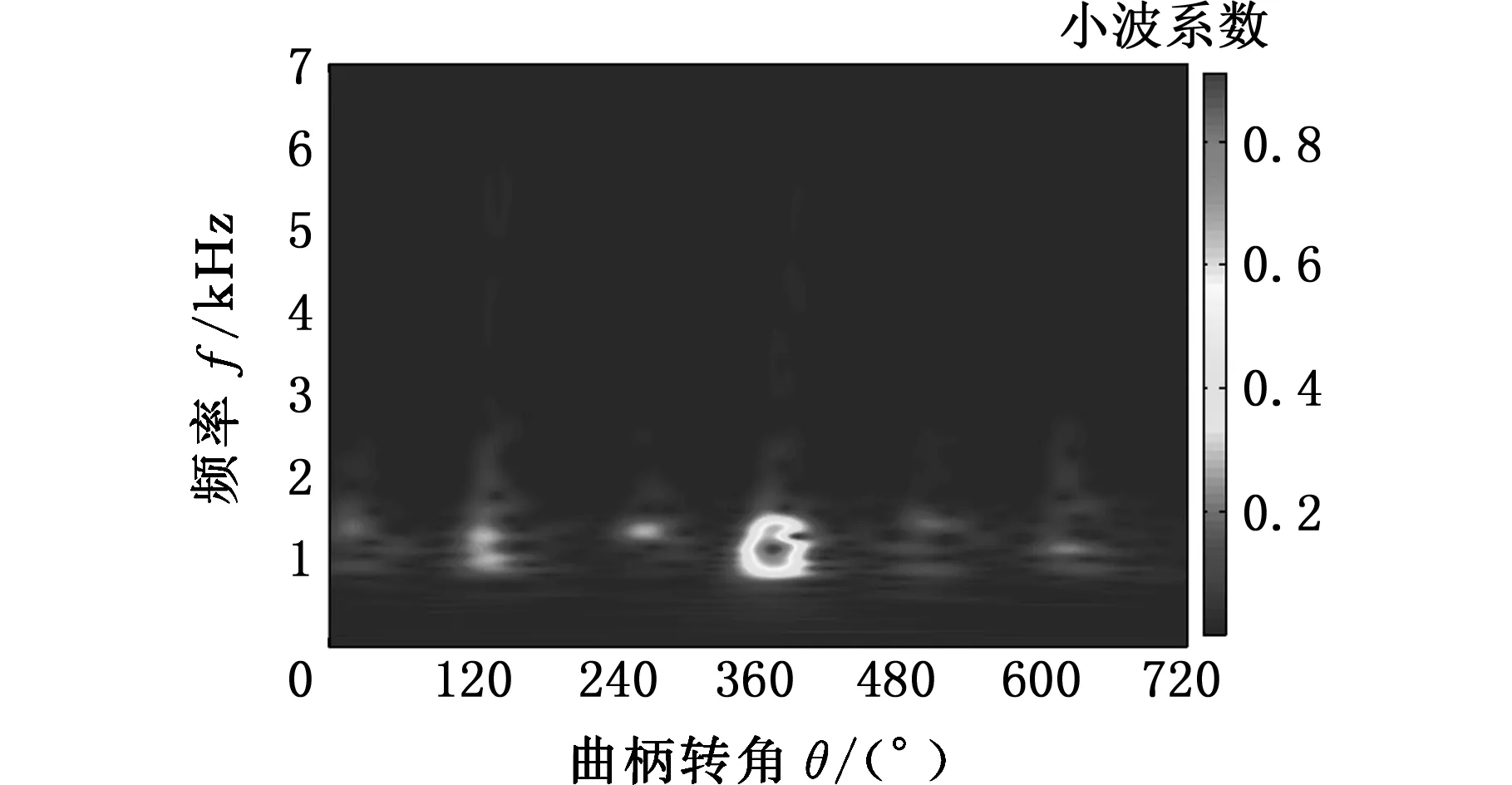
通过对图5中的计算结果进行分析后可知，分量IC1和分量IC2在时域波形上比较相似，并进一步地分析其频谱后发现，它们在频域上也比较相似，因此采用组合模态函数法将分量IC1和分量IC2组合为CMF12，SCMF12=SIC1+SIC2，组合分量CMF12的时域波形、频谱和时频图如图6所示。同时，通过分析发现分量IC3可能为活塞敲击信号，对其进行FFT分析和连续小波时频分析，结果如图7所示。

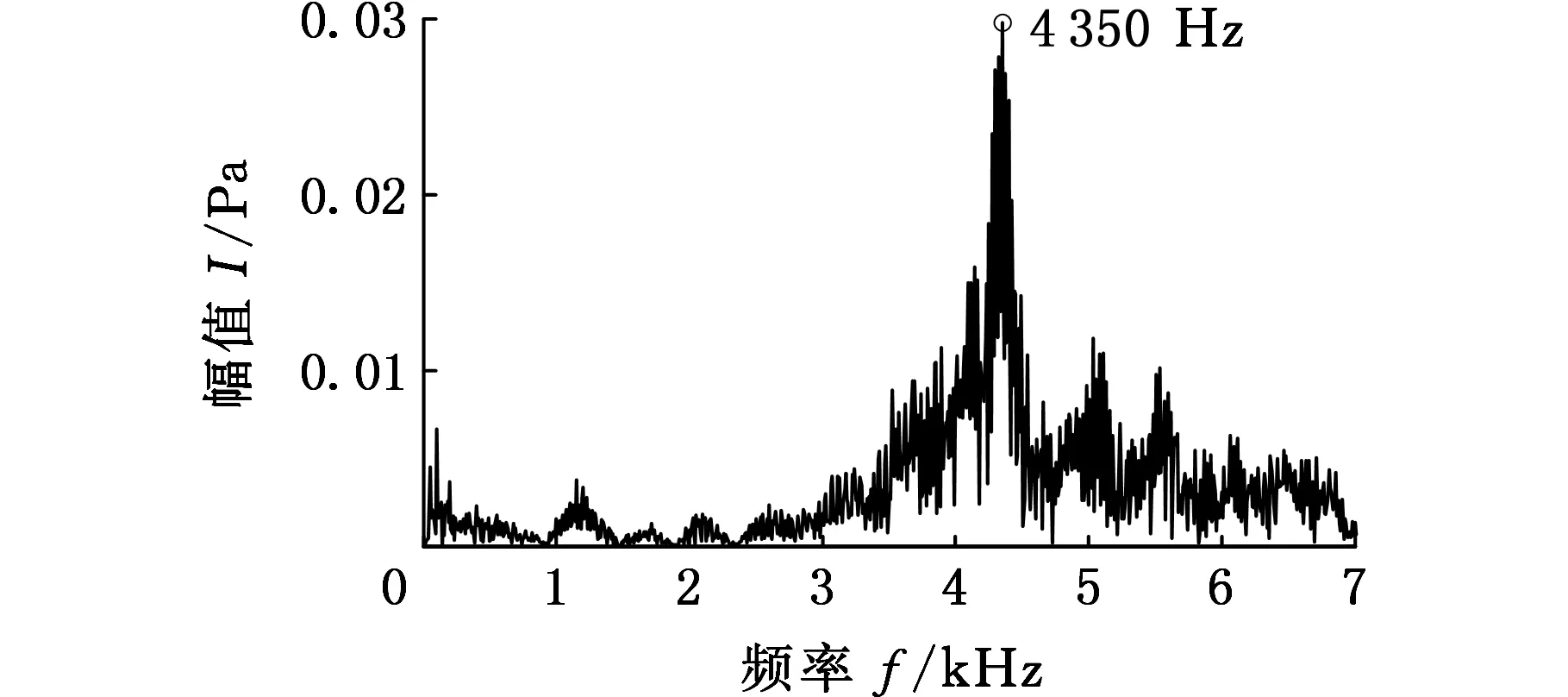
从图6中可知，组合分量CMF12时域波形的幅值在140°CA和380°CA左右变化较大，根据内燃机的先验知识，内燃机的发火顺序为1-5-3-6-2-4，第5号缸和第6号缸的发火角度分别在140°CA和380°CA左右，两缸工作间隔为240°CA，同时从频谱图中可以看出，组合分量CMF12的频率成分主要集中在4 350 Hz，结合缸压和缸盖振动的相干函数(图8)，在该频率成分附近，缸压和缸盖振动的相干性很好，缸压变化主要由缸内燃烧引起，通过缸压可以计算出燃烧信号[18]，这里主要对分离得到的分量进行定性判断，并进一步地结合时频图6c可知，在4 350 Hz附近，140°CA和380°CA左右的频率能量值较大，并且在380°CA左右的频率能量值要大于140°CA左右的频率能量值，这是因为测量的是第6号缸的缸盖振动信号，第5号缸是第6号缸的相邻缸，燃烧产生的振动信号会传递到第6号缸，但是要比第6号缸由于燃烧引起的缸盖振动信号小，因此可以判断组合分量CMF12为燃烧信号。

(a)时域波形

(b)FFT

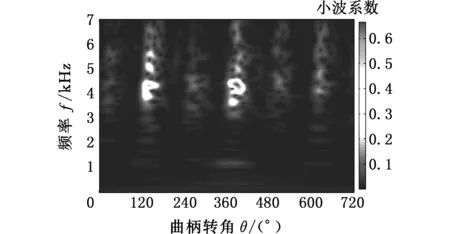
(c)CWT图6 CMF12的时域波形、FFT和CWT图Fig.6 The time domain waveform, FFT and CWT of CMF12

(a)时域波形

(b)FFT

(c)CWT图7 IC3的时域波形、FFT和CWT图Fig.7 The time domain waveform, FFT and CWT of IC3

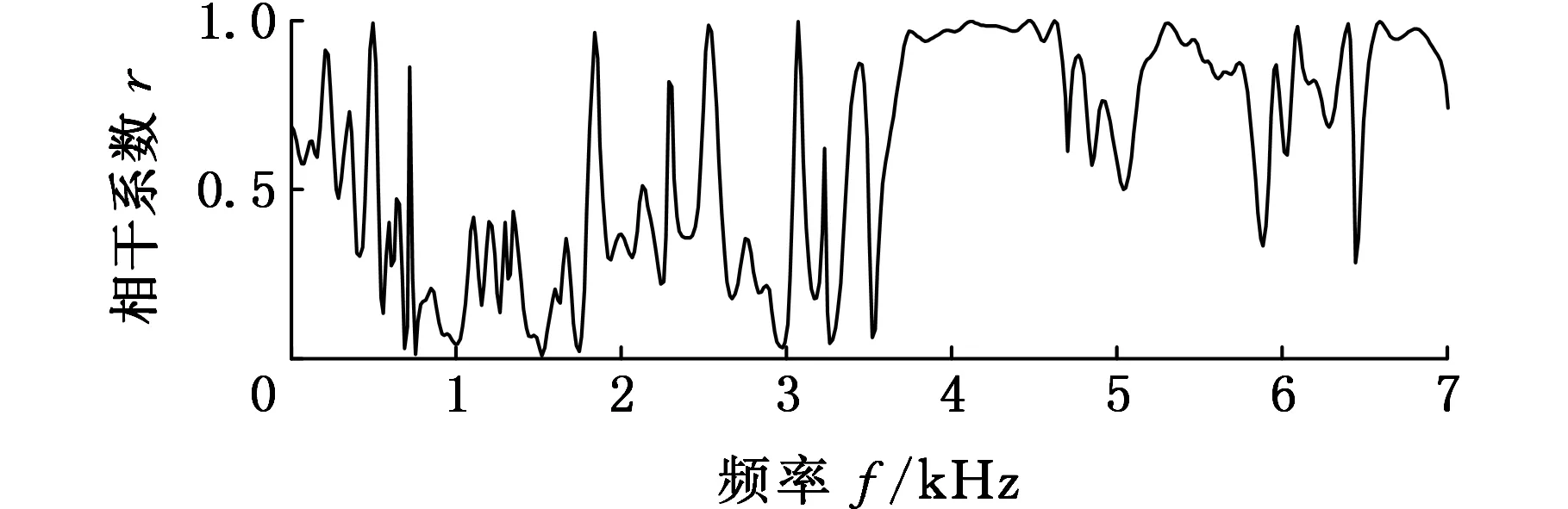
图8 1 000 r/min空载工况下的缸压和缸盖振动的相干函数Fig.8 The coherence function of cylinder pressure and cylinder head vibration of 1 000 r/min no-load condition

根据图7可知，分量IC3的时域波形的幅值在380°CA左右变化较大，同时在140°CA左右也有一定的变化，并且分量IC3的频率成分主要集中在1 150 Hz，根据缸压和缸盖振动的相干函数(图8)，在该频率成分附近，缸压和缸盖振动的相干性不好，同时由图7c可看出，在1 150 Hz附近，380°CA左右的频率能量值很大，且在140°CA左右也有一定的频率能量，内燃机的发火顺序1-5-3-6-2-4，与活塞敲击缸壁的时刻一致，将倒拖试验测得的活塞敲击振动信号频谱与分量IC3的频谱进行对比，如图9所示，可以发现活塞敲击振动频谱与分量IC3的频谱基本吻合，因此可以判断分量IC3主要为活塞敲击信号。但是在2 000 Hz附近，活塞敲击振动频谱较大，这可能是由于在倒拖试验中内燃机的其他运动部件产生的振动所致，还有待深入研究。

图9 1 000 r/min倒拖工况下的活塞敲击振动和分量IC3的频谱Fig.9 The spectrum of IC3 and piston slap vibration of 1 000 r/min drag condition

3.2 内燃机在2 100 r/min、25%负荷工况下缸盖振动信号的分离与识别

内燃机在2 100 r/min、25%负荷工况下的一个工作循环的缸压和缸盖振动信号如图10所示。

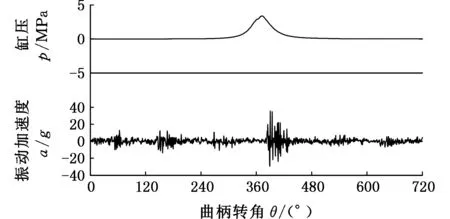
图10 缸压和缸盖振动信号Fig.10 Cylinder pressure and cylinder head vibration signals

对采集的单通道缸盖振动信号进行消除趋势项及滑动平均等预处理，然后对预处理后的信号进行分解，通过观察对比各个模态的中心频率后发现，当模态数K取为11时，有两个模态的中心频率为4 018 Hz和4 720 Hz，相距较近且出现了过分解，因此最佳的模态数取为10。

将通过变分模态分解算法计算得到的10个变分模态分量和预处理后的缸盖振动信号组成一个新的信号组，用RobustICA算法提取其独立成分，对得到的各个独立分量进行分析，并用组合模态函数法将时域和频域相似性较高的分量进行组合。通过分析后发现分量IC1和组合分量CMF23(SCMF23=SIC2+SIC3)可能为内燃机的燃烧信号和活塞敲击信号，下面结合频谱分析、连续小波时频分析、相干函数法、倒拖工况下的活塞敲击信号以及内燃机的先验知识对分离得到的结果进行进一步识别。分量IC1和组合分量CMF23的时域波形、FFT和CWT图分别见图11和图12。

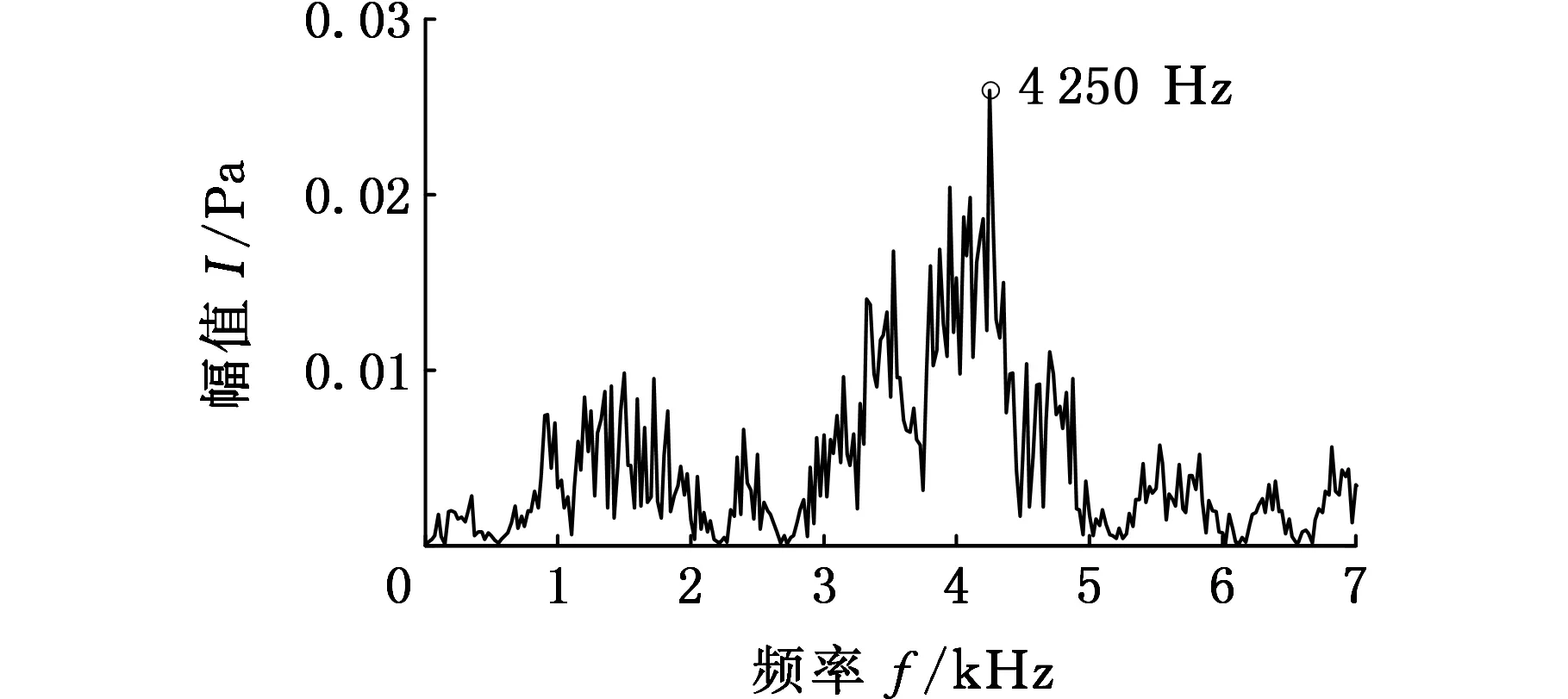
从图11可知，分量IC1的时域波形在380°CA处变化较大，经过FFT频谱分析后发现其频率主要集中在4 250 Hz，由图13可知，在该频率成分附近缸压和缸盖振动的相干性较好，缸压变化主要由缸内燃烧引起，内燃机的发火顺序为1-5-3-6-2-4，第6号缸的发火角度在380°CA处，与时频图上在该位置处的能量幅值较大一致，因此可判断分量IC1为燃烧信号。

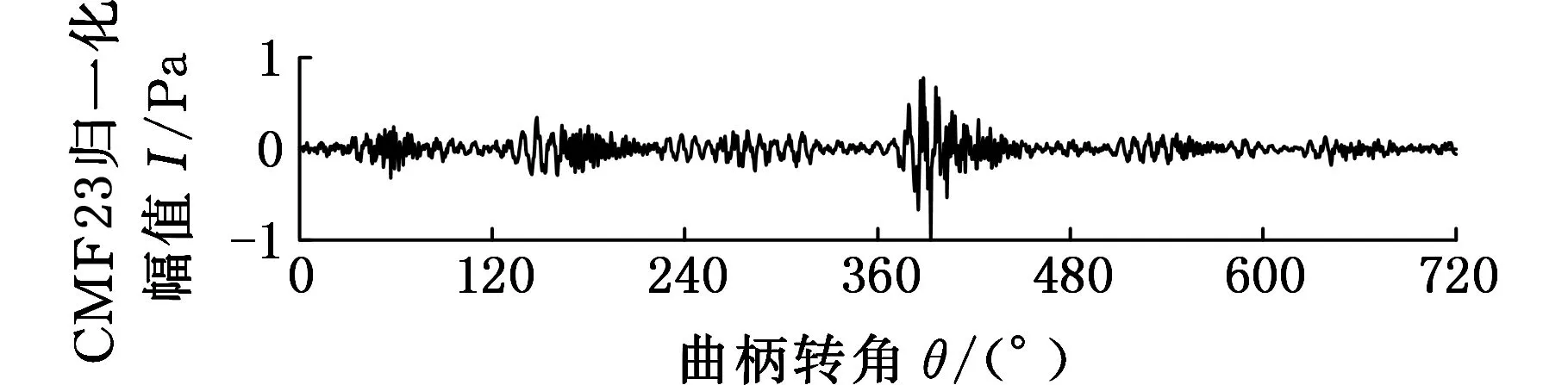
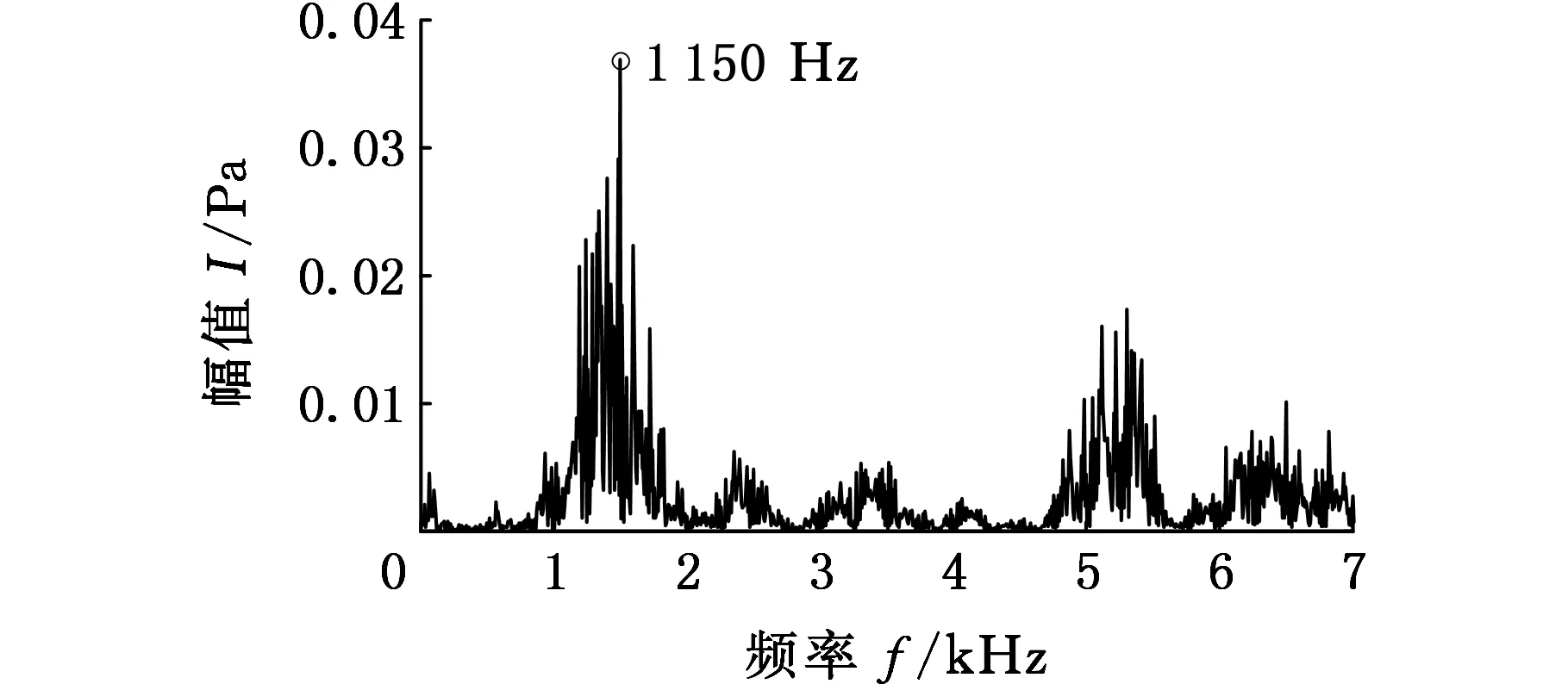
根据图12可知，组合分量CMF23的频率成分主要集中在1 500 Hz，从CWT时频图中可看出在380°CA处的能量幅值要大于在140°CA处的能量幅值，与内燃机的发火顺序1-5-3-6-2-4相对应，即5号缸和6号缸的发火角度分别在140°CA和380°CA处，其工作间隔为240°CA，并进一步地将倒拖工况下测得的活塞敲击振动信号频谱和组合分量CMF23的频谱进行对比，从图14中可看出，活塞敲击振动信号频谱和组合分量CMF23的频谱基本吻合，因此可判断组合分量CMF23主要为活塞敲击信号。但是活塞敲击振动信号频谱在500 Hz和2 500 Hz附近仍有其他频率成分，这可能是由于在倒拖工况时其他零部件运动时产生的，还有待进一步研究。

(a)时域波形

(b)FFT

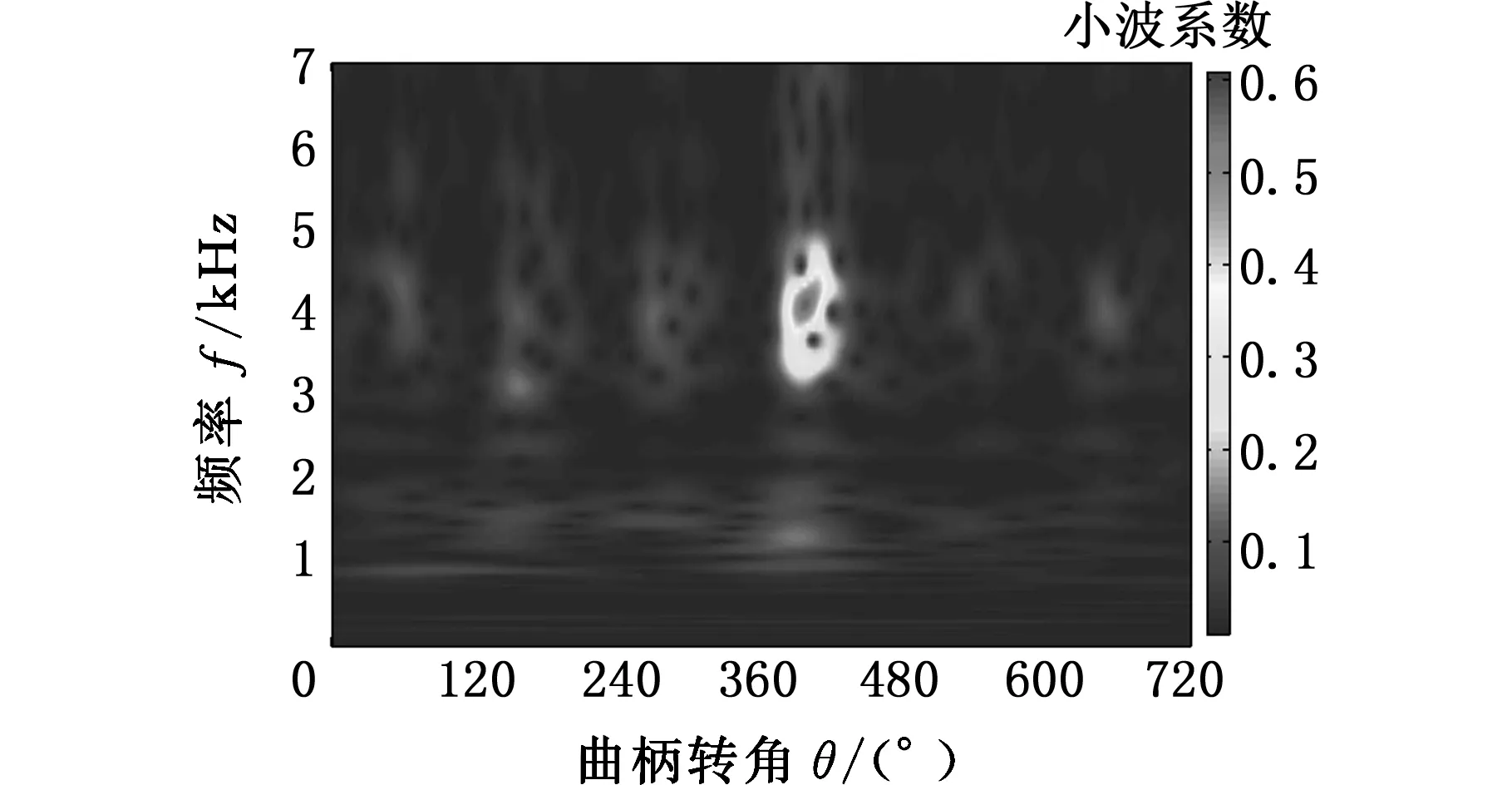
(c)CWT图11 IC1的时域波形、FFT和CWT图Fig.11 The time domain waveform, FFT and CWT of IC1

(a)时域波形

(b)FFT

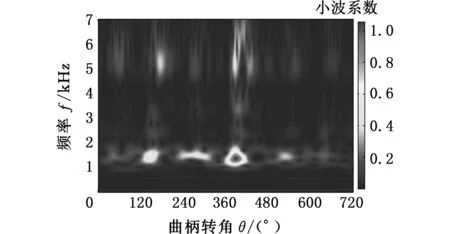
(c)CWT图12 CMF23的时域波形、FFT和CWT图Fig.12 The time domain waveform, FFT and CWT of CMF23

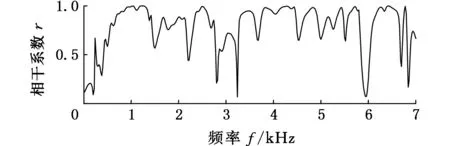
图13 2 100 r/min、25%负荷下的缸压和缸盖振动的相干函数Fig.13 The coherence function of cylinder pressure and cylinder head vibration of 2 100 r/min and 25% load

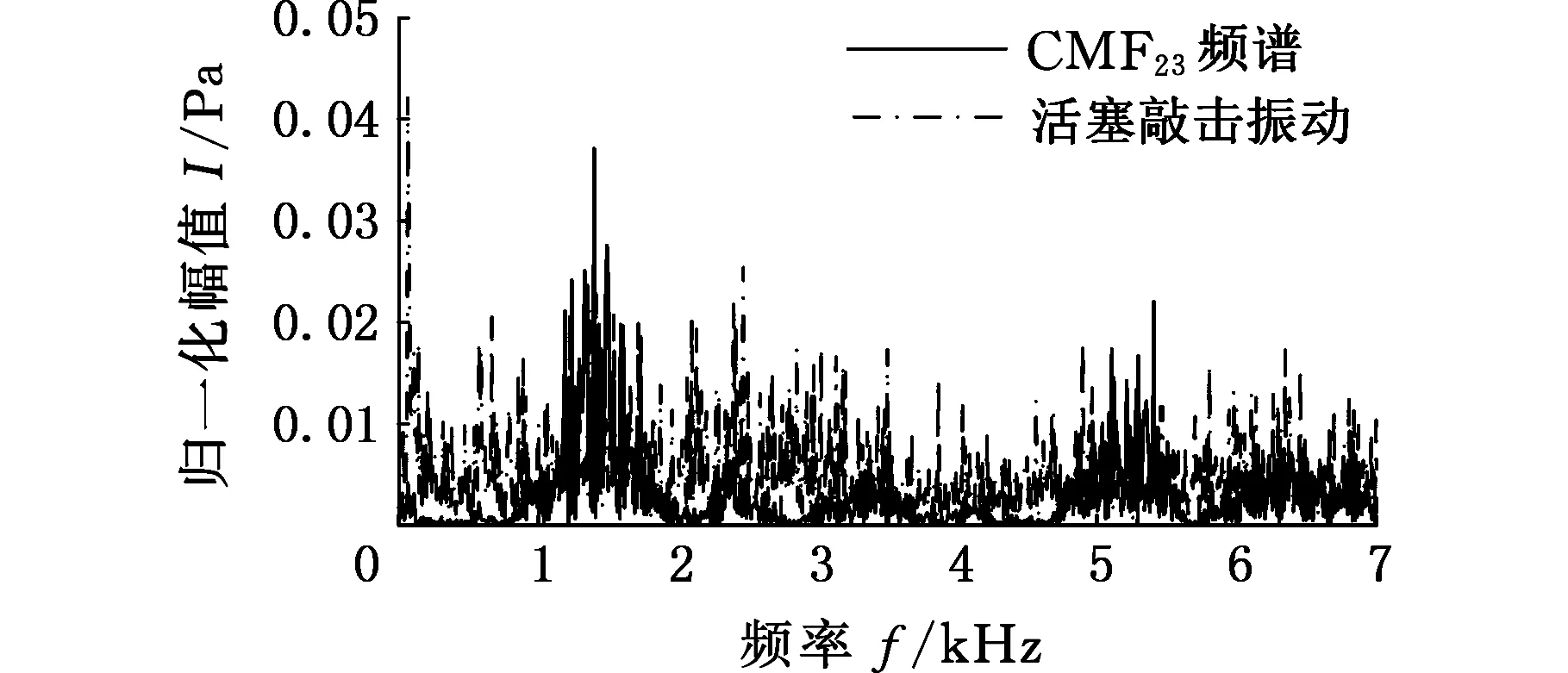
图14 2 100 r/min倒拖工况下的活塞敲击振动和分量CMF23的频谱Fig.14 The spectrum of CMF23 and piston slap vibration of 2 100 r/min and 25% load

4 结论

(1)通过试验测量内燃机的单通道缸盖振动信号后，用VMD算法、RobustICA算法及组合模态函数法，并结合频谱分析、连续小波时频分析、相干函数法及倒拖试验准确有效地分离识别出了内燃机的燃烧信号和活塞敲击信号。

(2)在内燃机1 000 r/min空载工况下，燃烧信号和活塞敲击信号的频率成分分别集中在4 350 Hz和1 150 Hz；在2 100 r/min、25%负荷工况下，燃烧信号和活塞敲击信号的频率成分分别集中在4 250 Hz和1 500 Hz。由此可看出燃烧信号的频率成分都集中在4 300 Hz附近，这主要是由于内燃机燃烧阶段的高频振荡所引起；但是活塞敲击信号的频率在不同工况下有一定的差别，主要是因为内燃机在转速较高负荷较大的工况下，活塞撞击缸壁的频率较高，撞击力较大，从而导致活塞敲击信号的频率较高。

参考文献：

[1] CHEN J, RANDALL R B, PEETERS B. Advanced Diagnostic System for Piston Slap Faults in IC Engines, Based on the Non-stationary Characteristics of the Vibration Signals[J]. Mechanical Systems & Signal Processing, 2016, 75:434-454.

[2] CHEN J, RANDALL R B. Intelligent Diagnosis of Bearing Knock Faults in Internal Combustion Engines Using Vibration Simulation[J]. Mechanism & Machine Theory, 2016, 104:161-176.

[3] 吴虎胜,吕建新,吴庐山,等.基于EMD和SVM的柴油机气阀机构故障诊断[J].中国机械工程, 2010,21(22):2710-2714.

WU Husheng, LYU Jianxin, WU Lushan, et al. Fault Diagnosis for Diesel Valve Train Based on SVM and EMD[J]. China Mechanical Engineering, 2010,21(22):2710-2714.

[4] 丁岩,邵毅敏.基于角域振动信号特征统计量的发动机故障分类方法[J]. 中国机械工程, 2014, 25(10):1374-1380.

DING Yan, SHAO Yimin. Engine Fault Classification Based on Characteristic Statistics of Vibration Signals in Angle Domain[J]. China Mechanical Engineering, 2014, 25(10):1374-1380.

[5] 刘建敏,李晓磊,乔新勇,等.基于EMD和STFT柴油机缸盖振动信号时频分析[J]. 噪声与振动控制, 2013(2):133-137.

LIU Jianmin, LI Xiaolei, QIAO Xinyong, et al. Time-Frequency Analysis of Vibration Signal from Cylinder Head of a Diesel Engine Based on EMD and STFT[J]. Noise and Vibration Control, 2013(2):133-137.

[6] LIU X, RANDALL R B. Blind Source Separation of Internal Combustion Engine Piston Slap from Other Measured Vibration Signals[J]. Mechanical Systems & Signal Processing, 2005, 19(6):1196-1208.

[7] LIU X, RANDALL R B, ANTONI J. Blind Separation of Internal Combustion Engine Vibration Signals by a Deflation Method[J]. Mechanical Systems & Signal Processing, 2008, 22(5):1082-1091.

[8] 康斌,向阳.独立分量分析在柴油机缸盖振动信号分离中的应用[J]. 武汉理工大学学报(交通科学与工程版), 2012, 36(4):753-756.

KANG Bin, XIANG Yang. Application of Independent Component Analysis to Decomposition of Engine Vibration Signal[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2012, 36(4):753-756.

[9] 韩春杨, 姚国凤, 赵建,等.柴油机振动信号盲分离组合算法[J]. 振动与冲击, 2014, 33(6):44-47.

HAN Chunyang, YAO Guofeng, ZHAO Jian, et al. Combination Algorithm for Blind Separation of Diesel Engine Vibration Signal [J]. Journal of Vibration and Shock, 2014, 33(6):44-47.

[10] DU X, LI Z, BI F, et al. Source Separation of Diesel Engine Vibration Based on the Empirical Mode Decomposition and Independent Component Analysis[J]. Chinese Journal of Mechanical Engineering, 2012, 25(3):557-563.

[11] HUANG N E, SHEN Z, LONG S R, et al. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-stationary Time Series Analysis[J]. Proceedings of the Royal Society: A Mathematical Physical & Engineering Sciences, 1998, 454:903-995.

[12] ŽVOKELJ M, ZUPAN S, PREBIL I. EEMD-based Multiscale ICA Method for Slewing Bearing Fault Detection and Diagnosis [J]. Journal of Sound and Vibration, 2016, 370: 394-423.

[13] ZHANG M, JIANG Z, FENG K. Research on Variational Mode Decomposition in Rolling Bearings Fault Diagnosis of the Multistage Centrifugal Pump[J]. Mechanical Systems & Signal Processing, 2017, 93:460-493.

[14] DRAGOMIRETSKIY K, ZOSSO D. Variational Mode Decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3):531-544.

[15] HYVARINEN A. Fast and Robust Fixed-point Algorithms for Independent Component Analysis[J]. IEEE Transactions on Neural Networks, 1999, 10(3):626-634.

[16] ZARZOSO V, COMON P. Robust Independent Component Analysis by Iterative Maximization of the Kurtosis Contrast with Algebraic Optimal Step Size [J]. IEEE Transactions on Neural Networks, 2010, 21(2):248-261.

[18] ANTONI J, DUCLEAUX N, NGHIEM G, et al. Separation of Combustion Noise in IC Engines under Cyclo-non-stationary Regime[J]. Mechanical Systems & Signal Processing, 2013, 38(1):223-236.