涡旋膨胀机的性能模拟

彭 斌 李要红 赵生显

1.兰州理工大学机电工程学院，兰州，7300502.兰州理工大学温州泵阀工程研究院，温州，325105

0 引言

随着全球气候问题的日益严重和不可再生资源的日益短缺，节能、减排、新能源的开发利用以及提高现有能源的利用效率已经成为当今世界各国研究的重要课题之一。工业余热、发动机余热、太阳能热、地热等中低品位热能的有效利用是解决能源问题的一个重要途径。有机朗肯循环(organic Rankine cycle，ORC)作为一种回收中低品位热能用于发电的技术，具有效率高、环境友好、结构简单等优点。ORC以有机物工质代替水作为动力循环系统，特别适合回收低品位热能，并且采用不同的有机物工质可回收不同温度范围的低品位热能。作为ORC 发电系统关键部件的涡旋膨胀机，其性能很大程度上影响着整个系统的综合性能，因此，对涡旋膨胀机性能的研究已成为工业余热回收研究课题中必不可少的内容[1]。

涡旋膨胀机所使用的型线主要有两类：等截面型线和变截面型线。等截面即涡旋齿为等壁厚；变截面即涡旋齿为非等壁厚。等截面型线因其固有特点，具有数学描述简单、涡旋齿承受的气体力波动较小、加工较为方便等优点，但不能充分利用毛坯材料，而且由于啮合特性的限制，设计的灵活性相对较差。如果增加等截面的压缩比，就必须增加涡旋齿的圈数，这样就会造成整机尺寸和轴向泄漏线长度增加，同时也延长了工质在工作腔中的停留时间，从而产生较大的泄漏。

国内外学者针对涡旋膨胀机的性能做了大量的研究工作[2-4]。对等截面型线的研究主要有：文献[5]对等截面涡旋式膨胀机的数学模型及仿真进行了研究；文献[6-8]以圆渐开线为几何基础，对涡旋膨胀机的数学模型以及动态仿真进行了大量研究。变截面涡旋膨胀机的研究多是以变截面涡旋压缩机的数学模型为基础，因它能以较少的圈数达到较高的压缩比而得到国内外学者的大量研究，而变截面涡旋膨胀机和压缩机在型线组成结构上是类似的。文献[9]研究了基于泛函的涡旋型线共轭啮合理论；文献[10-12]以变径基圆渐开线构建双涡圈型线，分析了变截面膨胀机的几何模型和摩擦损失模型；文献[13]对变基圆半径渐开线涡旋膨胀机进行了详细研究。

目前对等截面膨胀机和变截面膨胀机的数学模型研究较多，但对两者性能的比较多是定性分析，而鲜见定量分析，因此，本文以圆渐开线等截面膨胀机和组合型线变截面膨胀机为研究对象，从几何模型出发，根据质量和能量守恒建立涡旋膨胀机的数学模型，并通过对数学模型的求解，得出涡旋膨胀机工作腔内工质气体的压力、温度和质量随主轴转角的实际变化规律，定量地对涡旋膨胀机数学模型进行分析。

1 涡旋膨胀机几何模型

1.1 型线的生成

以圆渐开线作为等截面涡旋型线的基线，则涡旋齿内外圈型线方程

(1)

式中，rb为基圆半径；α为内外壁渐开线起始角；φ为基线基圆半径的展角；下标i和o分别表示内外壁线。

图1所示为等截面涡旋齿型线，齿头采用双圆弧加直线修正的方式，增加齿头强度，提高膨胀比。

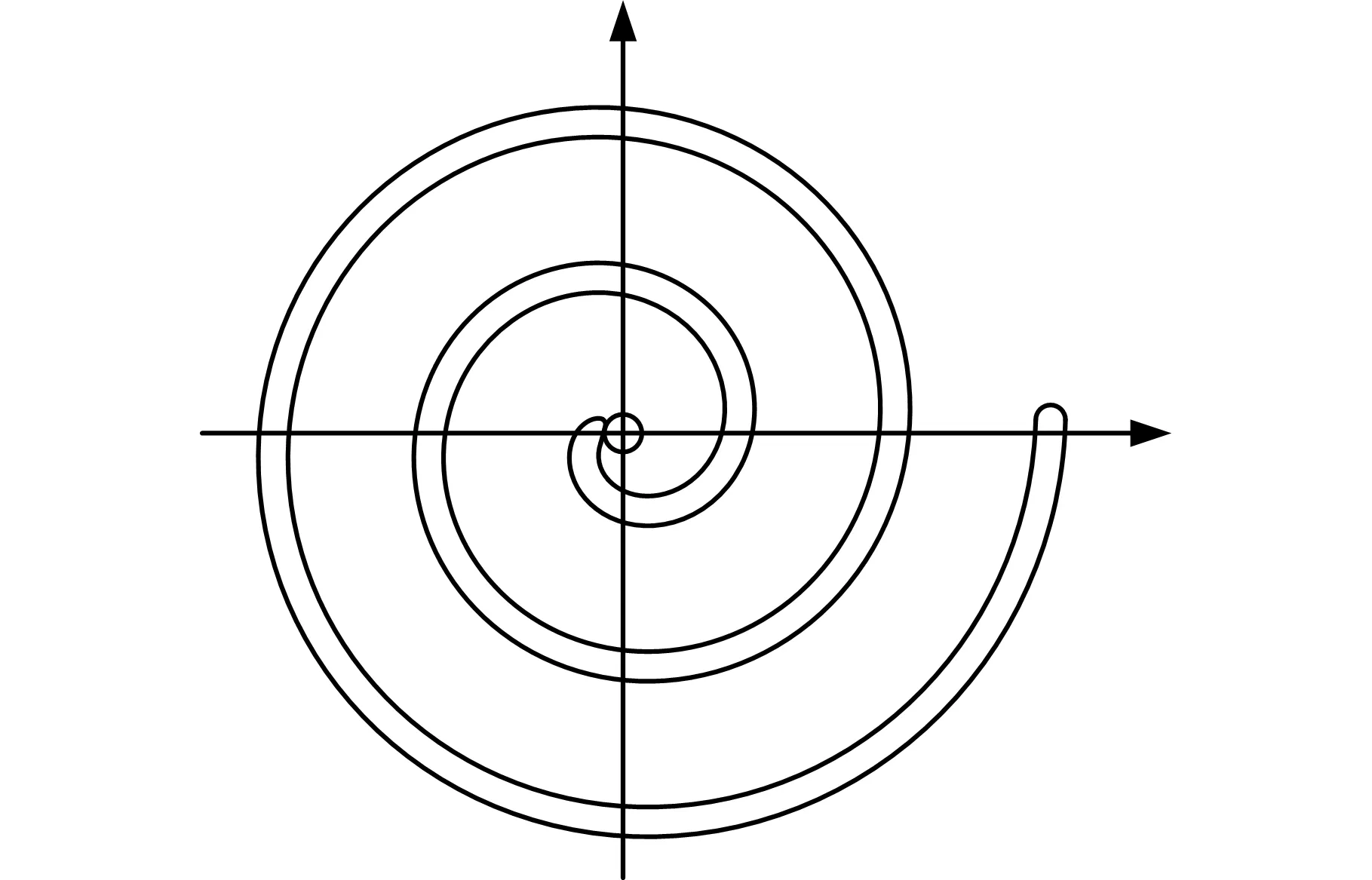
图1 等截面涡旋齿型线Fig.1 The scroll of constant thickness

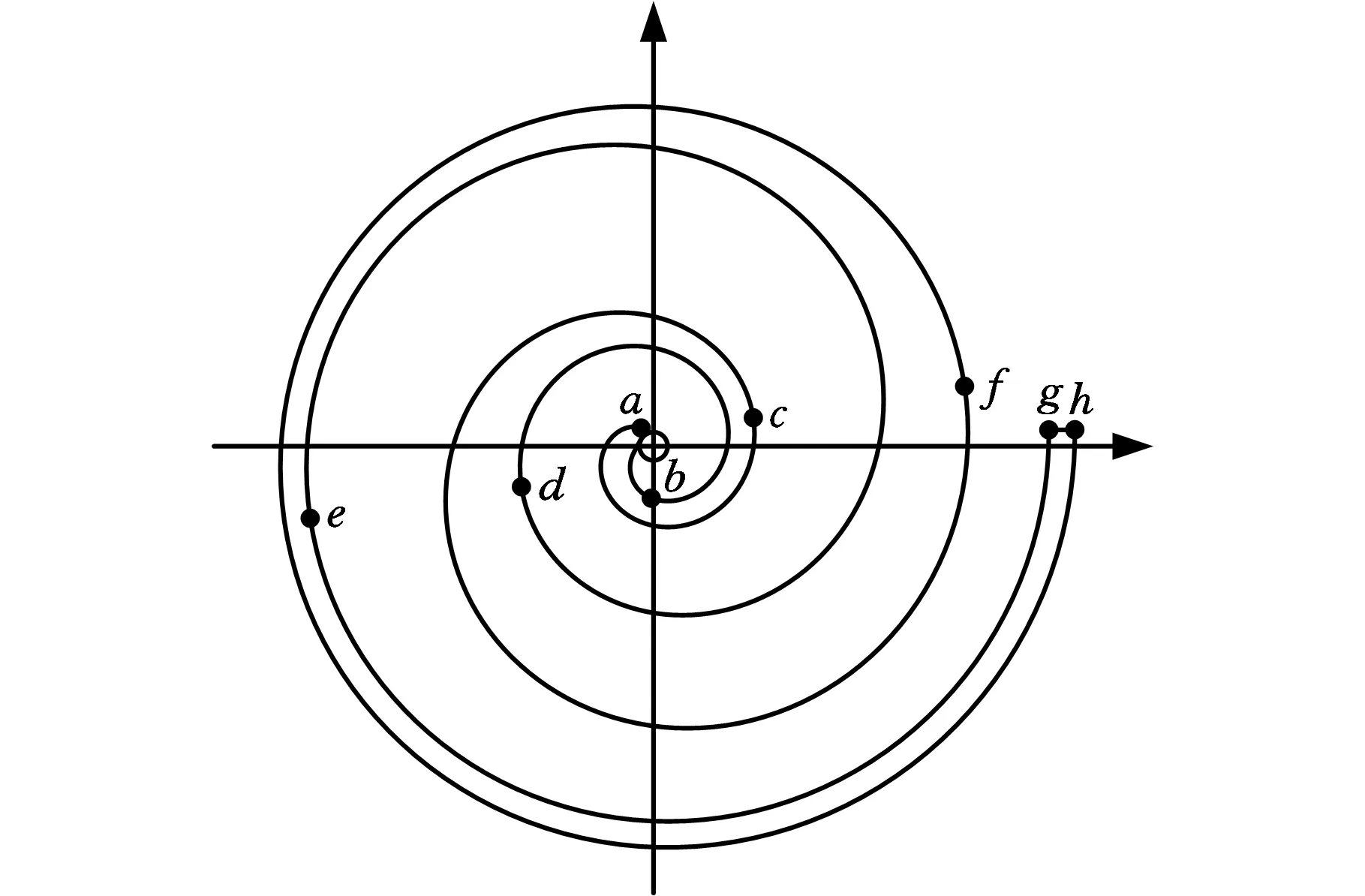
图2 变截面涡旋齿型线Fig.2 The scroll of variable thickness

1.2 工作腔容积的计算

1.2.1等截面膨胀机容积计算

在假定内外壁线渐开角相等的情况下，对等截面膨胀机工作腔容积进行计算[14]。

(1)等截面膨胀机吸气容积

V0=2HS′=2H(Si-So-SL)

(2)

其中，H为涡旋齿高度；Si为涡旋盘内壁面型线形成的面积；So为涡旋体壁厚部分投影面积；SL为两基圆之间围成的面积。它们的计算公式如下：

(3)

(4)

式中，Ro为公转半径；θ为曲轴转角。

(2)第i(i≥1)个膨胀腔的工作容积

Vi=πPt(Pt-2t)H[(2i+1)+θ/π]

(5)

式中，Pt为涡旋体节距；t为涡旋体壁厚。

(3)等截面膨胀机排气腔的工作容积

Vd=rbRoH[(2π-θ)(2φeπ+θ-3π)+
2(φeπ-π+α)sinθ+(π/2-α)sin2θ+2(1-cosθ)]

(6)

式中，φe为终端渐开角。

1.2.2变截面膨胀机容积的计算

由于组合型线的特殊性，所以在不同的工作过程中，工作腔的组成曲线不同[15]。

(1)工作腔完全由高次曲线组成时，工作腔的容积

V=HRo{Lh+[Rgh(φe)-Rgh(φs)]}

(7)

式中，Lh为高次曲线对应基线的弧长；Rgh(φ)为展角φ处的高次曲线展弦；Rgc(φ)为展角φ处的圆渐开线展弦。

(2)工作腔由高次曲线和圆渐开线组成时，工作腔的容积

V=HRo{Lh+Lc+[Rgc(φe)-Rgh(φs)]}

(8)

式中，Lc为圆渐开线对应基线的弧长。

(3)工作腔由圆渐开线和修正圆弧组成时，工作腔的容积

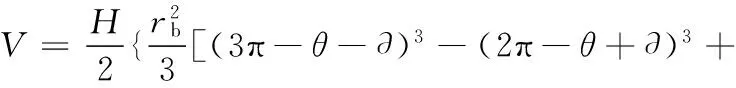
(9)

(10)

式中，γ为修正角；λ为修正圆弧中心角；θ*为开始排气角；β为修正展角；∂为齿头与y轴夹角；R为修正大圆弧半径；r为修正小圆弧半径。

(4)工作腔完全由修正圆弧组成时，工作腔容积

V=H(R2-r2)(θt-sinθt)/2

(11)

式中，θt为圆心角。

2 涡旋膨胀机的性能计算模型

涡旋膨胀机的运行工况比较复杂，为了使其数学模型在计算过程中简单易求，无论等截面膨胀机还是变截面膨胀机，模拟计算时均提出以下基本假设：①模拟计算研究的范围从进气开始到排气结束；②在任何时刻，膨胀机各工作腔内工质的状态是均匀的；③工质在膨胀腔内无相变，工质的泄漏量与工质携带总能瞬时达到平衡；④主轴转速恒定且工质为理想气体。

2.1 模拟计算控制方程

求解过程主要使用的控制方程如下[12]：

(1)膨胀腔内工质温度T随主轴转角θ的变化为

(12)

式中，p为工作腔内工质的压力；cV为工作腔内工质的质量定容热容；v为工作腔内工质的比容；ω为曲轴角速度；m为膨胀腔内工质质量；min为流入工作腔内工质的质量；mout为流出工作腔内工质的质量；h为工作腔内工质的比焓；hin为流入工作腔内工质的比焓；Q为工作腔与外界的热交换量。

(2)膨胀腔内工质质量m随主轴转角θ的变化为

(13)

(3)膨胀腔内工质质量流量

(14)

(15)

式中，ψ为流动系数；As为面积；ρh为高压侧密度；ph为高压侧压力；pL为低压侧压力；γc为压缩指数。

(4)工质在膨胀过程中的传热量

(16)

式中，cp为工作腔内工质的质量定压热容。

(5)理想气体的状态方程。

2.2 泄漏

涡旋膨胀机的泄漏主要包括由径向间隙引起的切向泄漏和由轴向间隙引起的径向泄漏。在进行径向和切向泄漏分析时，将间隙表示为高、低侧压力的函数，则径向泄漏面积[16]

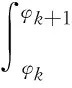
(17)

切向泄漏面积

Af=Hδf(ph,pL)

(18)

式中，δr(ph,pL)为径向泄漏系数；δf(ph,pL)为切向泄漏系数；L为径向泄漏线长度。

2.3 传热

根据传热学的基础知识，有温差的存在就会有传热现象的发生，热传递主要有热传导、热对流、热辐射三种方式。由于工质气体温度和涡旋膨胀机外壳、涡旋齿、涡旋盘底部以及周围环境的温度之间存在一定的温差，故在涡旋膨胀机正常工作的过程中，不可避免地会发生热量传递。工质气体与涡旋齿之间存在较复杂的传热，为了简化传热模型，忽略导热和辐射，只考虑它们之间的对流传热。

涡旋膨胀机进排气的传热可按照流体在圆管内强制对流换热计算，其关联式由Dittus- Boelter[17]确定。

涡旋膨胀机主要的传热为工作腔内的传热，其传热量的确定主要由三个参数计算，即传热系数、工质气体与壁面的温差和传热面积。使用螺旋板式换热器平均对流换热系数的计算方法来计算换热系数[18]：

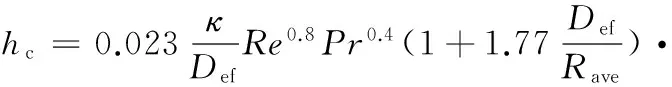
(19)

式中，κ为热导率；Def为当量直径；St为斯坦顿数；Re为雷诺数；Pr为普朗特数；Rave为平均半径；A为涡旋齿的面积。

当量直径定义为工作腔容积与涡旋齿壁面积之比：

Def=4V/A

(20)

平均半径Rave由下式确定：

Rave=rb[(φk-π/2)+(φk-1-π/2)]/2

(21)

Jang等[19]通过实验得出，从涡旋齿中心到齿末端上的温度随渐开角呈线性分布，即

(22)

式中，Ts1为渐开角φ1处的温度。

对于工作腔内传热面积的计算，主要有涡旋齿壁和涡旋盘顶部或底部面积两部分：在渐开角φk～φk-2π范围内，所形成的工作腔内涡旋齿壁的面积微分

dA=Hrb(φ-φ0)dφ

(23)

式中，φ0为中心渐开线起始角。

涡旋盘底部的面积微分

(24)

式中，φi0、φo0分别为涡旋齿内外壁渐开线发生角。

于是，传热量

(25)

式中，T(k,j)为第k个工作腔内主轴转角为θj时的温度；Tscr(φ)为中间温度；dA为传热面积(涡旋齿和涡旋盘)。

3 计算结果与分析

在理论分析的基础上，通过Fortran软件对数学模型进行模拟计算，图3为涡旋膨胀机数学模型模拟计算流程图。根据膨胀机几何结构和参数，首先求解出等截面膨胀机和变截面膨胀机工作腔的容积随主轴转角的变化曲线，然后由几何模型、传热模型、泄漏模型以及控制方程组计算出膨胀机工作腔的质量、温度和压力随曲轴转角的变化；最后可根据求解得到的工作腔工质压力并结合动力学模型和摩擦损失模型，采用Newton-Raphson 法计算膨胀机的动力参数，并得到等截面和变截面涡旋膨胀机的排气温度、质量流量和轴功率等性能参数[19]。与文献[12]和文献[20]相比较，涡旋膨胀机数学模型的求解结果有较高的准确度，验证了本文数值求解的正确性，为膨胀机的选择提供了参考依据。

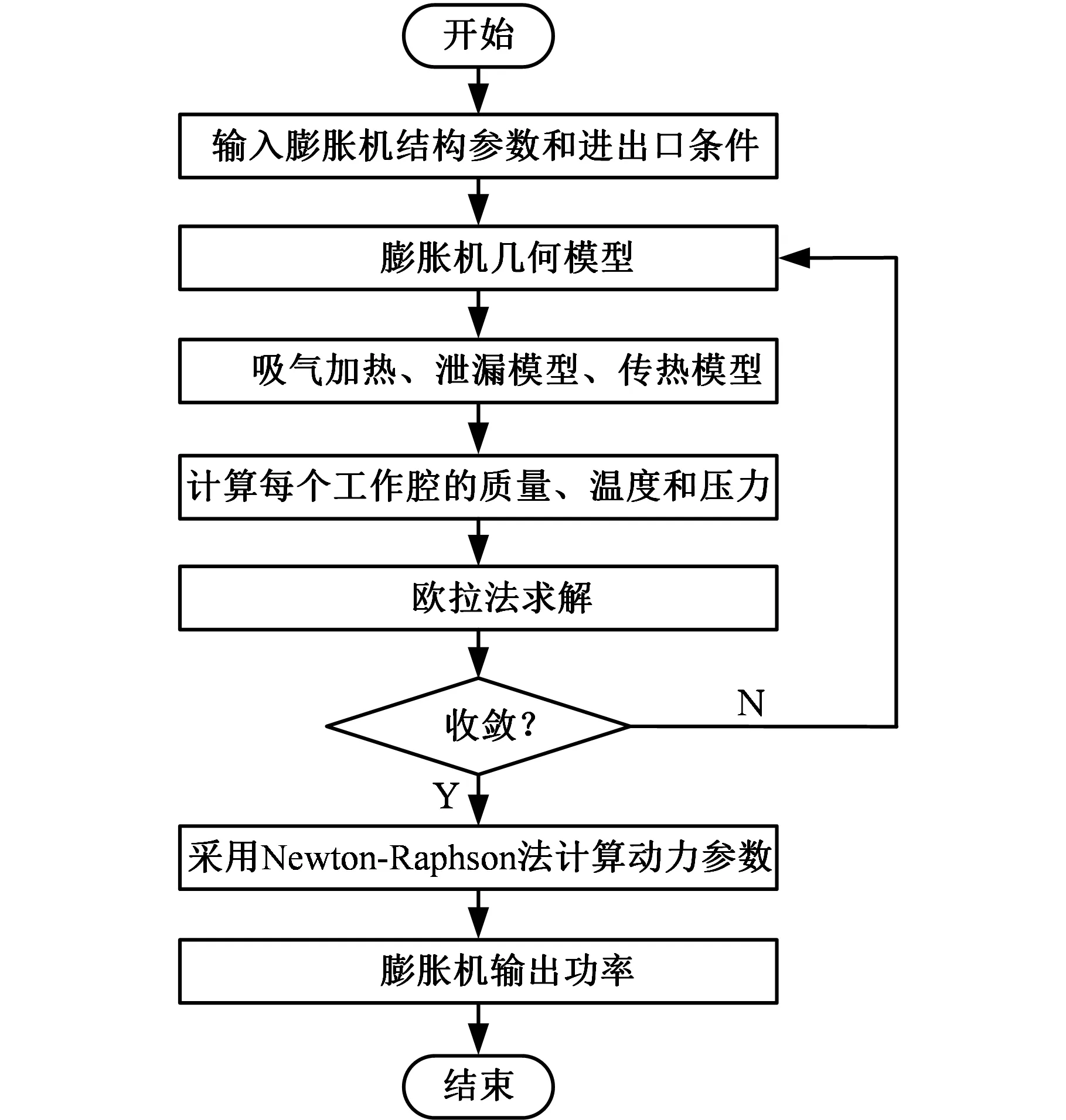
图3 求解流程图Fig.3 Solving process

表1为涡旋膨胀机型线参数，给出了等截面涡旋齿型线参数和变截面涡旋齿参数。

表1涡旋膨胀机几何参数

Tab.1Geometricparametersofscrollexpandermm

截面类型基圆半径rb壁厚t公转半径Ro齿高H等截面23.143.1420变截面22.520

上述两种膨胀机终端渐开角均为φe=21.46 rad，开始排气角φd=17.055 rad，圈数N=2.5，在上述数据相等的条件下，使用Fortran软件编程，求出两种膨胀机的工作腔容积、压力、温度和质量随主轴转角的变化，分别对曲线进行分析。下面分别对两者的容积、压力、温度和质量变化进行分析。

3.1 工作腔容积变化图

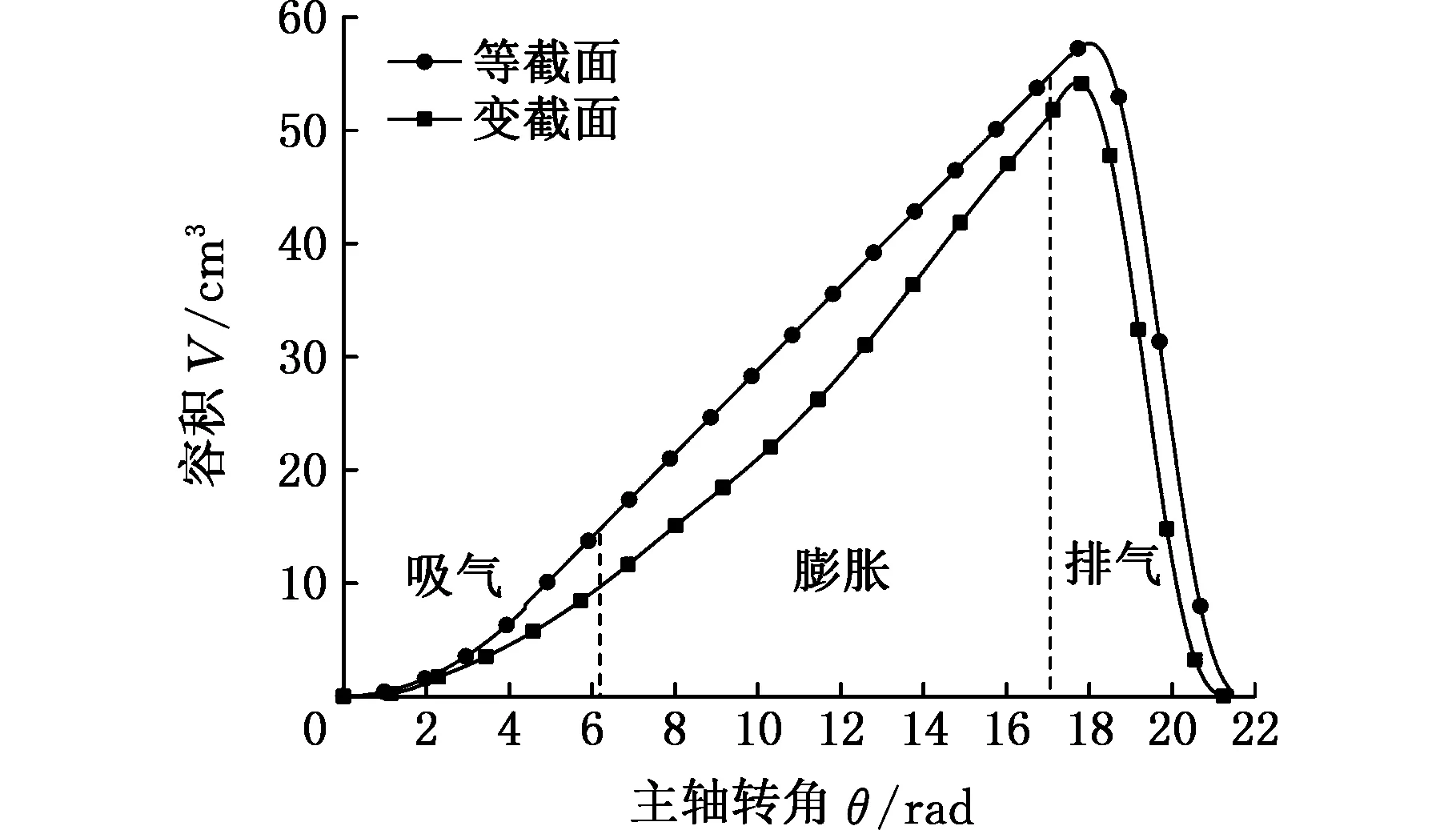
图4 工作腔容积随主轴转角的变化Fig.4 The change of various compressor chambers volume

图4为膨胀机工作腔容积随主轴转角的变化曲线，可以看出，两条曲线在吸气阶段，工质从吸气孔进入涡旋膨胀机，主轴转动一圈后进入膨胀阶段，膨胀过程体积逐渐增大，随着膨胀腔与排气腔的连通，开始进入排气阶段，直到排气结束。变截面涡旋膨胀机吸气容积与等截面膨胀机吸气容积相差不大，但是在膨胀阶段，由于变截面涡旋膨胀机减小了腔体数，容积小于等截面涡旋膨胀机，但是变截面膨胀机增大了膨胀终了的容积，而且吸排气基本达到了零余隙容积，提高了膨胀机效率。

3.2 工作腔压力和温度变化图

图5为工作腔内工质气体的压力和温度随主轴转角的变化曲线，可以看出，工质在进入膨胀机之后工质压力和温度均基本趋于稳定，之后开始膨胀，由于在进气结束开始膨胀之前，气体来不及进入膨胀腔，导致工质压力和温度有一定的增大，随着主轴转角的变化，工质的压力和温度逐渐减小，最后排出膨胀机。根据图4所示工作腔容积随主轴转角的变化趋势，由于变截面涡旋膨胀机工质膨胀时体积较大且泄漏较小，故变截面膨胀机膨胀腔工质的压力和温度明显高于等截面膨胀机的压力和温度，能增大膨胀比，从而提高膨胀机的功率。图5b中，在膨胀后期，变截面膨胀机温度较高，是由于膨胀阶段工作腔体积较大、压力较高且泄漏较低，使得膨胀腔的温度变化较为缓和；因为变截面膨胀机腔体数较少、泄漏低，在排气阶段，变截面膨胀机工质的温度高于等截面膨胀机工质的温度。

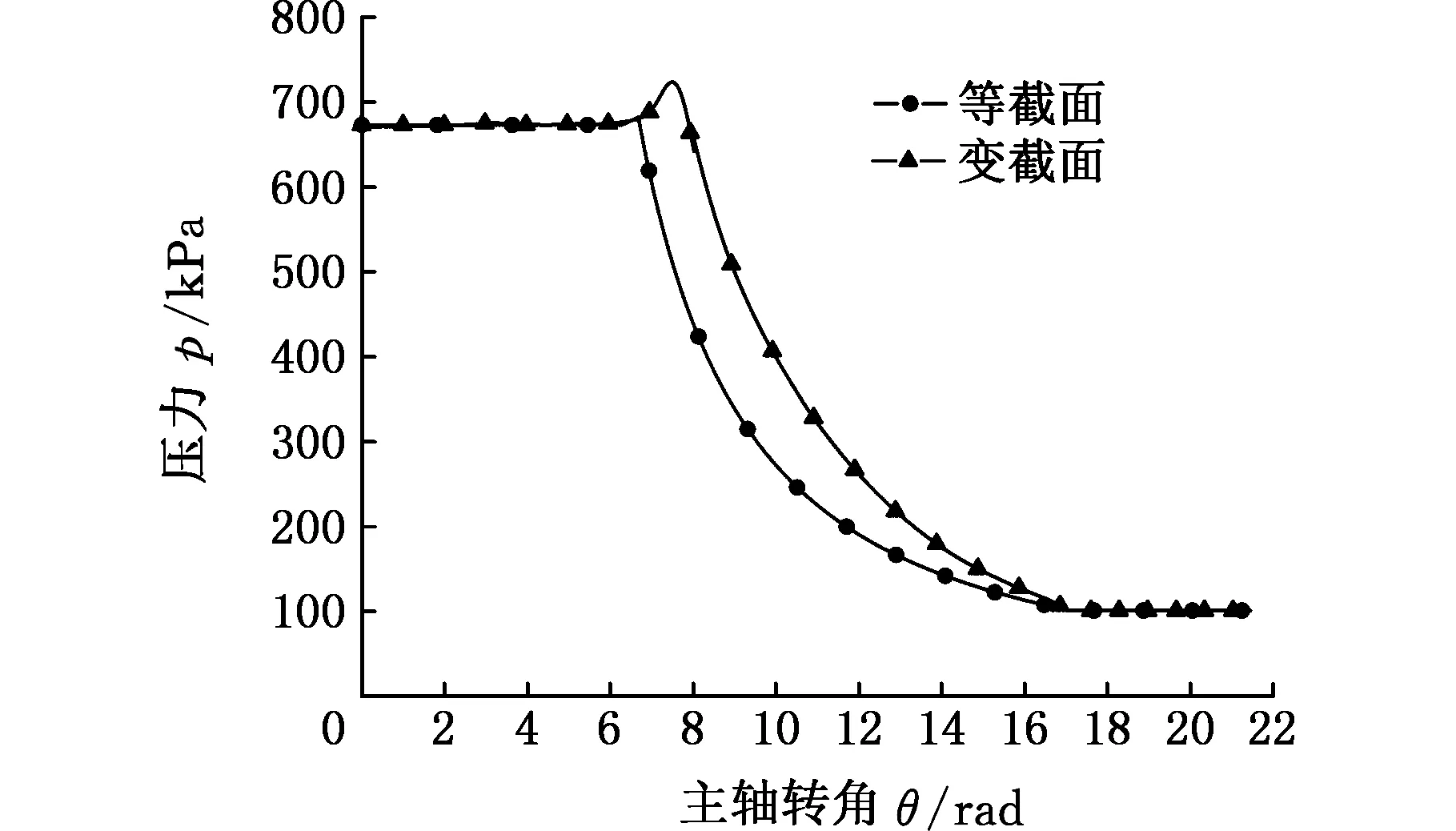
(a)工作腔压力曲线

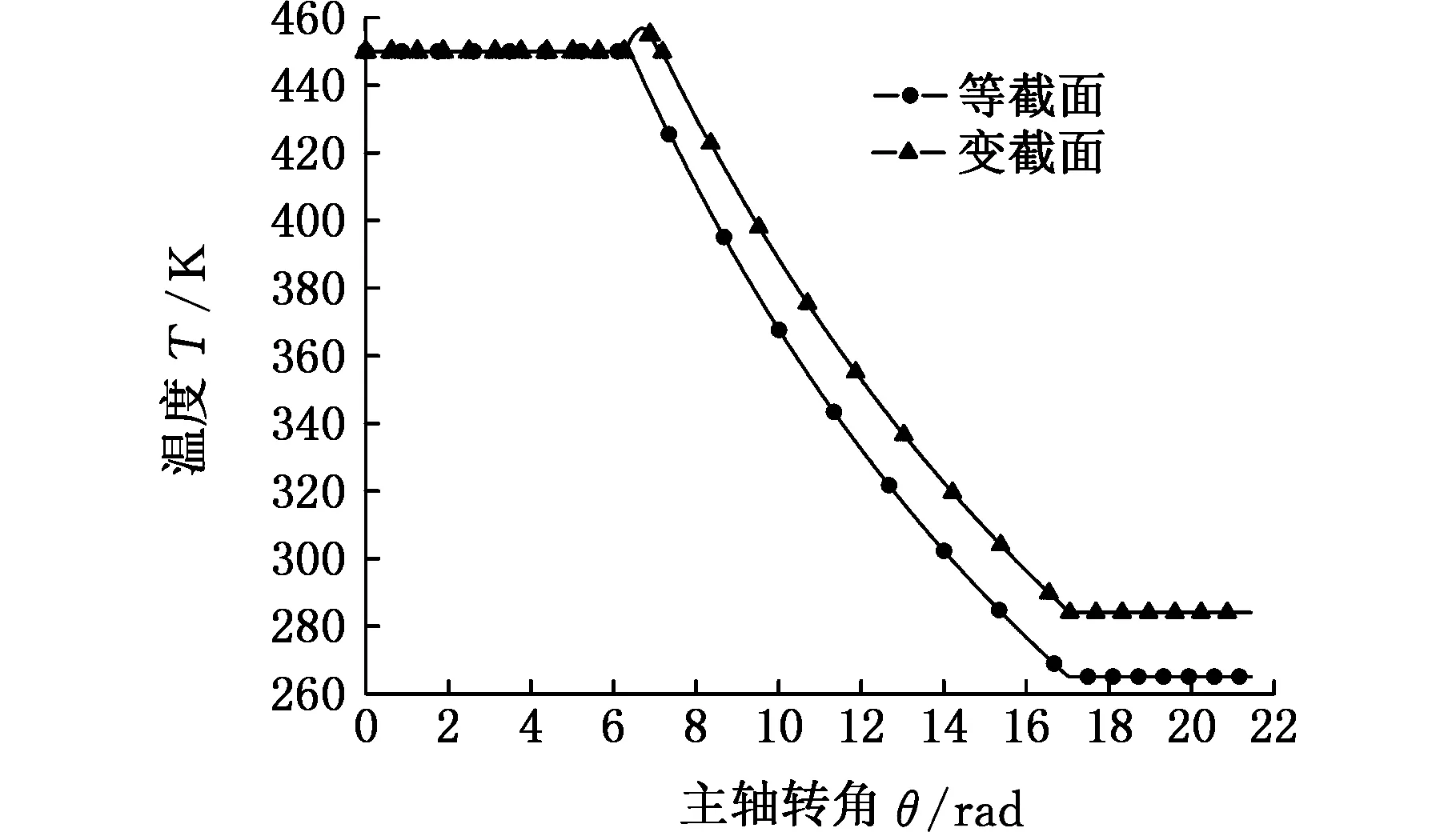
(b)工作腔温度曲线图5 工作腔压力和温度随主轴转角的变化Fig.5 The pressure and temperature varies with orbiting angle

3.3 工作腔质量变化图

图6为工作腔质量随主轴转角的变化曲线，曲线走向和容积曲线基本一致，随着主轴转角的变化，吸气阶段质量逐渐增大；到膨胀阶段趋于平缓；在排气阶段，由于动涡盘转速较高，质量有一定的积攒(稍有上升，之后逐渐减小，直至排气结束)。相同终端渐开角的条件下，变截面膨胀机的工质气体容积大于等截面膨胀机的工质气体容积，而且泄漏相对较小，因此，在膨胀阶段，变截面膨胀机质量较等截面膨胀机有所上升，两者走向一致。

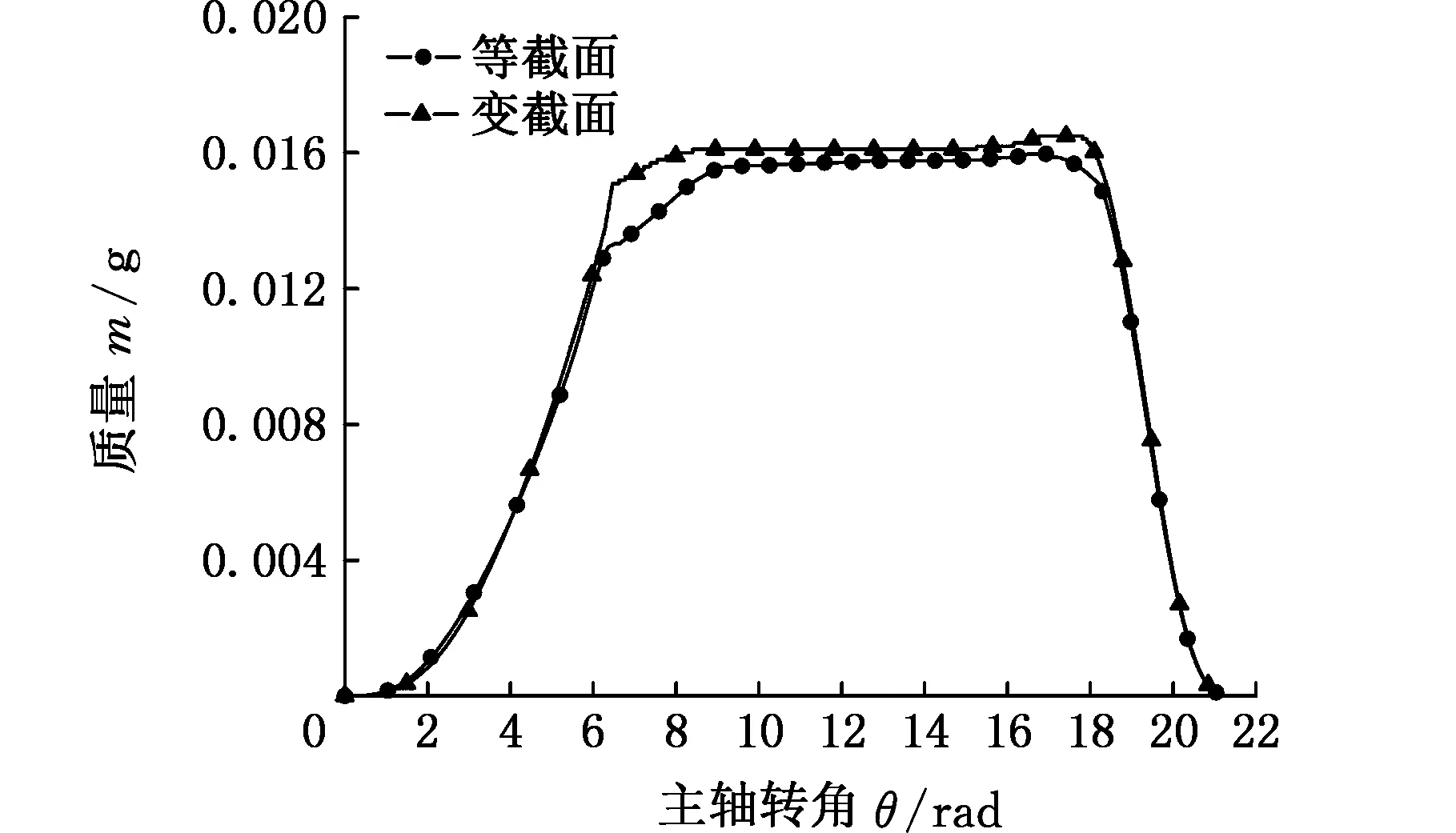
图6 工作腔质量随主轴转角的变化Fig.6 The mass varies with orbiting angle

3.4 膨胀机输出功率

图7所示为等截面和变截面涡旋膨胀机在转速为2 500 r/min、进气压力为683 kPa时输出功率随主轴转角的变化对比，可以看出，随主轴转角的增大，膨胀机输出功率先减小后增大。主轴转角在0～π时，由于齿头型线组成相同，变截面和等截面输出功率基本相等，之后因为变截面膨胀机涡旋齿型线较短，泄漏较小，其输出功率大于等截面输出功率。

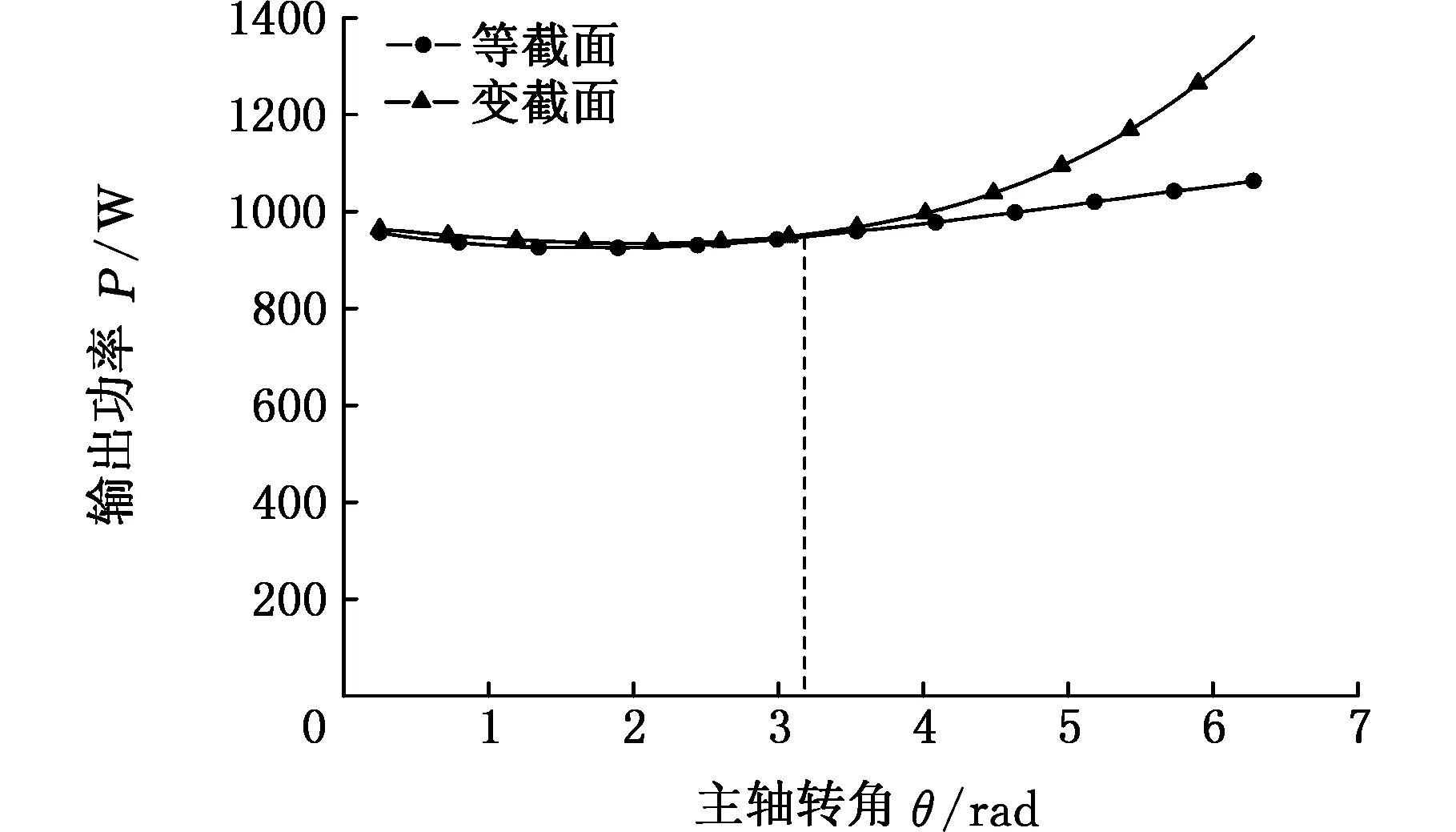
图7 输出功率随主轴转角变化Fig.7 Output power varies with orbiting angle

表2所示为等截面涡旋膨胀机和变截面涡旋膨胀机排气时刻的容积、压力和质量数据对比分析，其中，ε为涡旋膨胀机膨胀机内容积比，即膨胀终了与吸气结束的工质体积之比。

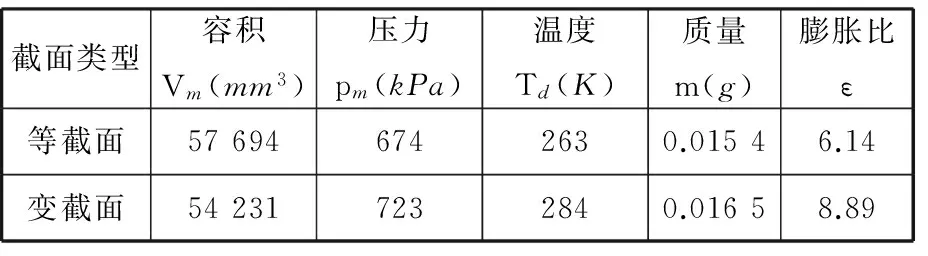
表2 结果对比

从表2中可以看出，两者容积差为3 463 mm3，最大压力差pe=49 kPa，质量相差不大，变截面膨胀机内容积比比等截面膨胀机要大。可见，相比变截面涡旋膨胀机，等截面涡旋膨胀机性能参数要好。

4 结论

对等截面涡旋型线膨胀机与变截面涡旋型线膨胀机的几何模型进行对比，得到两者的工作腔容积随主轴转角变化规律；根据能量和质量守恒定律，得到等截面膨胀机与变截面膨胀机数学模型，采用欧拉法和Newton-Raphson 法得到了实际介质在工作腔中质量、温度和压力的变化规律；通过对等截面膨胀机和变截面膨胀机的数学模型进行对比，在进气压力和转速相同的条件下，分别得出等截面膨胀机和变截面膨胀机输出功率的变化规律，变截面膨胀机通过改变涡旋齿型线的组成可减小腔体内部泄漏，增大膨胀比，提高膨胀机的机械效率。模拟计算的求解结果表明变截面涡旋膨胀机整体性能要高于等截面涡旋膨胀机。

参考文献：

[1] 中国能源中长期发展战略研究项目组.中国能源中长期(2030～2050)发展战略研究: 可再生能源卷[M].北京：科学出版社, 2011:1-20.

China Energy Long-term Development Strategy Research Project Team .China’s Energy Medium and Long Term (2030～2050) Development Strategy Research: Renewable Energy Volume[M].Beijing:Science Press, 2011:1-20.

[2] 高鹏, 江龙, 王丽伟.有机朗肯循环模拟及涡旋式膨胀机的性能研究[J]. 制冷学报, 2014, 35(1): 53-57.

GAO Peng, JIANG Long, WANG Liwei. The Simulation of ORC and Experimental Study on Scroll Expander[J]. Journal of Refrigeration, 2014, 35(1): 53-57.

[3] 贾甲, 李炅, 黄磊，等.小型ORC 系统膨胀机容积流量试验装置研究[J]. 低温与超导, 2016, 44(5): 48-50.

JIA Jia, LI Jiong, HUANG Lei,et al. Research on Volume Flow Test Equipment of Expander in Small ORC System[J]. Cryogenics and Superconductivity, 2016, 44(5): 48-50.

[4] 杨绪飞, 戚风亮, 刘秀龙，等.有机朗肯循环膨胀机入口过热度实验[J]. 化工进展, 2016, 35(7): 2007-2014.

YANG Xufei, QI Fengliang, LIU Xiulong,et al. Experiment on Expander Inlet Superheat of Organic Rankine Cycle[J].Chemical Industry and Engineering Progress， 2016， 35(7)： 2007-2014.

[5] 王吉岱，梁新军,杨兴华，等.涡旋式膨胀机数学模型及仿真研究[J]．压缩机技术, 2012, 5(5): 13-16.

WANG Jidai, LIANG Xinjun,YANG Xinhua,et al. Mathematical Model and Simulation Study on Scroll Expander[J]. Compressor Technology, 2012, 5(5): 13-16.

[6] (日)森下悦生, 等(邓立文译). 涡旋式压缩机的几何理论[J].流体机械，1985(10):40-50.

(Japan) MORISHITA E. DENG Liwen,Trans. Geometrical Theory of Scroll Compressor[J]. Fluid Machinery, 1985(10):40-50.

[7] CHEN Y, HALM N, BRAUN J, et al.Mathematical Modeling of Scroll Compressors. Part II：Overall Scroll Compressor Modeling[J]. International Journal of Refrigeration, 2002, 25(6): 751-764.

[8] 侯国莲， 胡国强，毕珊珊，等.涡旋式膨胀机的非线性数学模型及动态仿真[J]. 动力工程学报, 2012, 32(8): 606-611.

HOU Guolian, HU Guoqiang,BI Shanshan,et al. Nonlinear Mathematical Model and Dynamic Simulation of Scroll Expanders[J]. Power Engineering, 2012, 32(8): 606-611.

[9] 王立存, 陈进, 张贤明, 等. 基于泛函的制冷涡旋压缩机变壁厚涡旋型线理论及形状优化[J]. 中国机械工程， 2010, 21(16): 1898-1901.

WANG Licun, CHEN Jin, ZHANG Xianming,et al. Study on Geometry Theory of Variable Wall Thickness Scroll Profiles and Shape Optimization Based on Functional Theory[J]. China Mechanical Engineering, 2010, 21(16): 1898-1901.

[10] LIU Y G, TANG Y H, CHANG Y C .et al. Optimum Design of Scroll Profiles Created from Involute of Circle with Variable Radii by Using Finite Element Analysis[J]. Mechanism and Machine Theory, 2012, 55: 1-17.

[11] LIU Y G, HUNG C H, CHANG Y C. Study on Involute of Circle with Variable Radii in a Scroll Compressor[J]. Mechanism and Machine Theory, 2010, 45(11): 1520-536.

[12 ] 彭斌,孙迎. 变截面涡旋压缩机数学模型及试验研究[J]. 机械工程学报, 2015, 51(14): 185-191.

PENG Bin, SUN Ying. Investigation of Mathematical Modeling and Experiment for Variable Thickness Scroll Compressor[J]. Chinese Journal of Mechanical Engineering, 2015, 51(14): 185-191.

[13] 王吉岱, 张臻臻, 魏军英. 变基圆半径渐开线涡旋膨胀机的研究[J]. 流体机械, 2014, 42(6): 33-36.

WANG Jidai, ZHANG Zhenzhen, WEI Junying. Research of the Scroll Expander with Variable Base Circle Radius Involute[J]. Fluid Machinery, 2014, 42(6): 33-36.

[14] MORISHITA E,SUGIHARA M,INABA T,et al. Scroll Compressor Analytical Model[C]// International Compressor Engineering Conference. West Lafayette,1984:487.

[15] 刘振全. 涡旋式流体机械与涡旋压缩机[M].北京:机械工业出版社, 2009：28-62.

LIU Zhenquan. The Scroll Type Fluid Machinery and the Scroll Compressor[M]. Beijing: Mechanical Industry Press, 2009：28-62.

[16] QIANG J G, PENG B, LIU Z Q. Dynamic Model for the Orbiting Scroll Based on the Pressures in Scroll Chambers. Part I: Analytical Modeling[J]. International Journal of Refrigeration, 2013, 36 (7): 1-20.

[17] INCROPERA F P, DEWITT D P. Fundamentals of Heat and Mass Transfer[M]. New York: John Wiley & Sons, 1996:23-40.

[18] JANG K, JEONG S. Experimental Investigation on Convective Heat Transfer Mechanism in a Scroll Compressor[J]. International Journal of Refrigeration, 2006, 29(5): 744-753.

[19] JANG K, JEONG S. Temperature and Heat Flux Measurement Inside Variable Speed Scroll Compressor[C]// 20th International Congress of Refrigeration.Sydney,1999: 293-302.

[20] PENG Bin, ZHU Bingguo, LEMORT V. Theoretical and Experimental Analysis of Scroll Expander[C]//23rd International Compressor Engineering Conference.West Lafayette,2016:2450.