运动解耦和低耦合度选择顺应性装配机器手臂并联机构的设计及其运动分析

沈惠平 许 可 杨廷力

常州大学现代机构学研究中心，常州，213016

0 引言

具有运动解耦特性的低耦合度三平移一转动输出的选择顺应性装配机器手臂(selective compliance assembly robot arm,SCARA) 并联机构(parallel mechanism，PM)的控制、轨迹规划以及运动学和动力学分析较为简单，可以较好地满足现代生产实际需求,因此，提出运动解耦、低耦合度新型SCARA并联机构具有重要的学术意义和使用价值。

近十年来，国内外学者不断研究运动解耦的并联机构。YEN等[1]研究了一种三自由度移动解耦并联机构的动力学模型，对其运动学与控制特性进行了分析；张志胜等[2]发明了一种运动解耦的XY向精密定位平台；童幸等[3]通过重新定义输出参数的方法，仿真分析了3种锻造操作机的解耦性；石志新等[4]基于单开链结构原理，先后构造了一种全解耦三平移并联机构和一类新型五自由度解耦并联机构；ALTUZARRA等[5]以具体实例阐述了如何通过支链选择及装配方式实现少自由度操作手部分解耦的问题；GLAZUNOV[6]用螺旋理论的方法研究了解耦并联机构的设计方法；张帆等[7]提出了球面转动并联机构运动解耦的拓扑条件；LEGNANI等[8]设计了特定位形下解耦和各向同性的六自由度并联机构；窦玉超等[9]提出了一种一平移两转动完全解耦的并联机构。

沈惠平等[10]对国内外已有的2～6个自由度运动解耦并联机构进行拓扑结构及其运动解耦性分析，提出了基于基本运动链(basic kinematics chain，BKC)合成与分解、基于子并联机构等效支链、基于合理选取基点，以及基于移动副平行、垂直配置等4种运动解耦设计方法，并设计了15个运动解耦并联机构。

KRUT等[11]提出了一类可实现三平移动一转动的四自由度并联机器人Heli4。GOGU[12]基于线性变换理论与进化形态学，提出了一组具有完全各向同性的并联机构。罗玉峰等[13]基于方位特征(position and orientation characteristics, POC)集的并联机构设计基本理论，综合设计出了多种具有SCARA运动输出的并联机构，并对它们进行了分类。XIE等[14]运用Grassmann线性几何法和Atlas法，综合设计出了一组四自由度SCARA并联机构。LI等[15]提出了一种具有4个相同四自由度支链的SCARA并联机构。但这些三平移一转动并联机构，大多数采用4条相同的复杂约束支链，其动平台的转动能力较小；在动平台上附加转角增大装置，可增大动平台的转动能力，但使动平台质量分散、增大，影响了机构动力学性能的改善；同时，它们的耦合度均较大(κ=2)，因此，其位置正解求解十分困难，影响构型优选、实时控制和误差分析。

综上，不难发现，目前兼有运动解耦特性和低耦合度(κ=0，1)的SCARA并联机构还较少。本文根据基于POC方程的并联机构拓扑结构设计理论[16,18]，设计出一种转角较大、运动解耦且耦合度低的四自由度SCARA并联机构，并对其位置正解、工作空间、动平台转角空间及机构奇异性进行了分析。

1 机构设计及拓扑分析

1.1 机构设计

图1 新型(RPa3R)2R-2RSS机构及其参数标注Fig.1 A novel PM(RPa3R)2R-2RSS and itsparameterization

根据基于POC方程的并联机构拓扑结构设计理论[16,18]，笔者设计的具有部分运动解耦、低耦合度(κ=1)的新型SCARA并联机构如图1所示[17-18]，静平台0与动平台1用2条相同的无约束支链 RSS、1条含有子并联机构(RPa3R)的混合支链 (RPa3R)2R连接，为方便，机构记为(RPa3R)2R-2RSS。

该机构的混合支链(RPa3R)2R是这样构成的：1个转动副(R11)连接由4个球副(S1、S2、S3、S4)组成的平行四边形(parallelogram, Pa)的短杆S1S2；短杆S3S4和由3个平行转动副构成的支链(R41‖R42‖R43)连接，且S3S4的连线和转动副R43轴线垂直，从而构成含1个回路的子并联机构(R‖Pa3R)；同时，短杆S3S4再串联2个平行转动副构成支链(R12‖R13)。

2条无约束支链可任意布置，取静平台0上相邻的4个转动副相互垂直，即R11R41R31R21。

1.2 POC集

由文献[16,18]可知，串联、并联机构的POC集方程分别为

(1)

(2)

式中，MJi为第i个运动副的POC集；Mbj为第j条支链末端的POC集；MPa为机构动平台的POC集。

该机构混合支链(HSOC)中，4个球副(4S)组成的平行四边形等价于2个移动副和2个转动副串联而成的支链，因此，子并联机构的2条支链的拓扑结构可记为

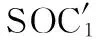
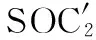
串联的2个转动副的拓扑结构为

该机构的POC集计算如下：

(1)选定动平台1上任一点为基点。

(2)确定HSOC末端构件的POC集。设b为子并联机构输出杆上的点，则由式(1)、式(2)得b点处的POC集：

(3)

其中，t、r分别表示移动和转动，下同，则

(3)确定动平台的POC集。无约束支链 (RSS)的POC集为3T3R，因此，由式(2)有

(4)

即动平台1可产生3个平移和1个绕转动副R13轴线的转动。

1.3 自由度

并联机构的自由度公式[16]为

(5)

(6)

(1)确定第一个回路的独立位移方程数ξL1。因第一个独立回路为上述子并联机构(RPa3R),则由式(6)得

由式(5)得该子并联机构的自由度：

(2)确定第二个回路的独立位移方程数ξL2。第二个独立回路由混合支链和一条无约束支链S23-S22-R21组成。由式(6)得

由式(5)得第二个子并联机构的自由度：

(3)确定第三个回路的独立位移方程数ξL3。第三个独立回路由上述第二个子并联机构和S33-S32-R31组成。由式(6)得

(4)确定机构自由度。由式(5)得该机构的自由度：

因此,由式(4)知，若取机架上的4个转动副为主动副R11、R21、R31、R41，则动平台1产生3T1R的输出运动。

1.4 耦合度

由基于单开链(SOC)的机构组成原理知，任一机构可分解为一系列单开链，第j个单开链(SOCj)的约束度为

(7)

式中，mj为第j个单开链的运动副数；fi为第i个运动副的自由度(不含局部自由度)；Ij为第j个单开链的驱动副数。

一组有序的v个单开链可构成一个独立回路数为v的基本运动链，对一个基本运动链而言，须

(8)

因此，耦合度为

(9)

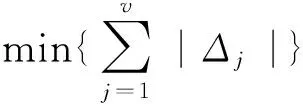
由式(7)可知，该机构包含的3条单开链及其约束度分别为

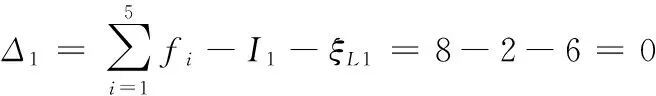
由(8)式可知，因Δ1=0，则由单开链SOC1构成第一个基本运动链BKC1；因Δ2+Δ3=0，则由SOC2、SOC3构成第二个基本运动链BKC2。由式(9)可知，这两个基本运动链的耦合度分别为

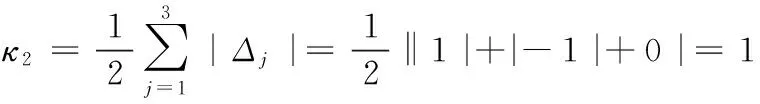
这样，该机构只包含2个基本运动链，其耦合度分别为0、1。因此，BKC1易得到位置正解解析解；对于BKC2，易得到仅含1个虚拟变量的一元高次封闭位置方程，并可求得其位置正解数值解[19-20]，从而求出机构的位置正解。

2 机构位置分析

2.1 基于单开链的机构位置正解求解方法

由式(7)可知，单开链有约束度为正值、零、负值三种形式，因此，基于单开链的位置正解封闭求解建模方法如下：

(5)用Mathematica软件对上述位置方程进行符号处理，得到一元高次的位置正解封闭方程。

(6)用非线性方程的一般求解方法(迭代法、二分法等)或直接应用Mathematica软件求解位置方程。

2.2 位置正解求解

已知：输入角θ1、θ2、θ3、θ4，求动平台1上P点的坐标(x,y,z)及转角α。

如图1所示，设机构静平台0为正方形，与静平台0相连接的4个转动副R11、R21、R31、R41分布在各边的中点。不失一般性，在静平台0上建立OXYZ坐标系，O为静平台0的重心，X轴垂直R11的轴线，Y轴平行于R11的轴线；在等腰直角三角形的动平台1上建立PUVW坐标系，P点与转动副R13重合，U轴、V轴分别与S33R13、S23R13重合；Z轴、W轴则由右手笛卡儿坐标系法则确定。为理解方便，将该机构俯视展开，如图2所示。

图2 机构的俯视展开表达Fig.2 Plan view of PM

该机构的结构参数如下：正方形静平台0的边长为2l1，动平台1直角边长为l2；R11a=R21S22=R31S32=R41R42=l3(l3≠l1)，ab=S22S23=S32S33=R42R43=l4；其余杆长分别为S3b=S3R43=l5，cR12=l6，R12b=R13c=l7。设R11a、R31S32与X轴正向的夹角为θ1、θ3；R21S22、R41R42与Y轴正向的夹角为θ2、θ4，如图1所示；设U(V)轴与X(Y)轴正向的转角为动平台姿态角α；R12R13与X轴正向的夹角δ*为虚拟角值，如图2所示。

2.2.1建立机构位置方程

易知，在静坐标系OXYZ下，静平台1上4个转动副R11、R21、R31、R41的坐标分别为(l1,0,0)、(0,-l1,0)、(-l1,0,0)、(0,l1,0)；点a、球副S22、S32及转动副R42的坐标分别为(l1+l3cosθ1,0,l3sinθ1)、(0,-l1+l3cosθ2,l3sinθ2)、(-l1+l3cosθ3,0,l3sinθ3)、(0,l1+l3cosθ4,l3sinθ4)。

(1)BKC1的位置求解。易知，由SOC1构成BKC1。由ab=R42R43=l4，有

(10)

由式(3)可知，子并联机构(RPa3R)中短杆S3S4上b点的输出为两平移(2T)，因此，在机构运动过程中，构件S3S4只能在OYZ平面内运动，且始终与Y轴重合，因此，xb=0即转动副R43的坐标为(0,yb+2l5,zb)。

将R43的坐标代入式(10)，并整理得

Ayb+Bzb=C

(11)

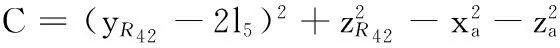
A=0时，

(12)

A≠0时，

(13)

D=A2+B2E=2(BC+zaA2)

(2)BKC2的位置求解。易知，由SOC2、SOC3构成BKC2。

①对SOC2(Δ2>0)而言。由图2知，转动副R13坐标为(l6cosδ*，yb+l6sinδ*，zb+2l7)，即动平台p点坐标分量为

(14)

上标*表示该物理量为虚拟角δ*的函数，下同。

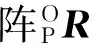
则

根据S22S23=l4，建立约束方程：

整理得

A1sinα+B1cosα+C1=0

(15)

A1=2l2x*B1=2l2(yS22-y*)

进一步，得

(16)

②对SOC3(Δ3<0)而言。在SOC3(Δ3<0)上应建立约束方程。S33的绝对坐标为

由S32S33=l4，建立位置约束方程：

(17)

2.2.2用Mathematica对位置方程进行符号处理

令t=tan(α*/2)，用Mathematica对式(17)进行符号处理，得

(18)

A2=(x*+l2-xS32)2+(y*-yS32)2+

B2=4l2yS32-4l2y*

C2=(l2-x*+xS32)2+(y*-yS32)2+

将α*的值代入式(18)，得

(19)

f=2A1A2+B2gg=B1-C1

(20)

令u=tan(δ*/2)，对式(20)展开并整理得

(21)

(22)

其中，G0、G1、…、G6为常系数，具体数值见文献[20]。

2.2.3求解位置方程

用非线性高次方程的一般求解方法(迭代法、二分法等)或直接应用Mathematica软件求出式(22)的实根，再由式(14)可得到机构动平台P点坐标；进一步，由式(16)(或R13、S33的位置)可求动平台的姿态角α。

由式(14)知，x=φ(θ1,θ2,θ3,θ4)，z=φ(θ1,θ4)，y=f(θ1,θ2,θ3,θ4)，α=η(θ1,θ2,θ3,θ4)，即z仅由θ1、θ4决定，因此，该机构具有输入-输出部分运动解耦性。

2.3 位置逆解分析

已知：动平台P点的坐标(x,y,z)和姿态角α，求输入角θ1、θ2、θ3、θ4。

2.3.1求b点坐标

由cR12=l6，建立约束方程：

(23)

解之有

(24)

2.3.2求输入角θ1、θ2、θ3、θ4

位置正解已求出球副S23、S33的坐标，现由4个从动臂ab、S22S23、S32S33、R42R43的杆长条件，建立如下约束方程：

(25)

(26)

(27)

(28)

由式(25)～式(28)可得

(29)

i=1,2,3,4

综上可知，当动平台P点的坐标和姿态角α已知时，输入角θ1、θ2、θ3、θ4各有两组解，b点的坐标有两组解，故逆解数为2×16=32，因此，动平台有32种构型。

2.4 正逆解验证

参考ABB机器人I4R的尺寸参数，两个平行四边形和输入杆的尺寸参数与之相同[21]，即l3=350 mm，l4=800 mm；其他结构参数分别为l1=300 mm，l2=150 mm，l5=100 mm，l6=200 mm，l7=25 mm。

(Ⅰ)输入角θ1、θ2、θ3、θ4分别为62.185 4°、128.454 6°、134.557 2°、47.626 9°。考虑该机构实际工作构型，取zb>0；根据式(22)，整理得

f(u)=(1.889 1-1.407 0u+1.071 7u2-1.110 2u3+
0.913 5u4+0.524 0u5+4.980 2u6×10-2)×1016

用Mathematica解得其实根：u1=-7.719 1，u2=-3.944 0；再代入式(14)、式(16)，得到位置正解，如表1中Ⅰ组数据所示，其中，No.2组正解所对应的装配构型如图3a所示。

(Ⅱ)输入角θ1、θ2、θ3、θ4分别为50°、140°、140°、50°。取zb>0，由式(22)，整理得

f(u)=(5.016 65-5.927 57u+4.020 35u2-
4.787 76u3+3.571 50u4-1.007 62u5-
0.096 78u6)×1016

同样，解得其实根分别为u1=-13.448 6，u2=1.206 98；再代入式(14)、式(16)，解得的位置正解如表1中Ⅱ组数据所示。

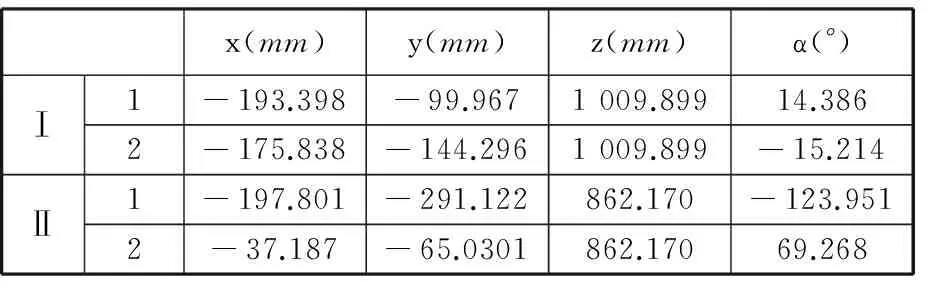
表1 位姿正解数值

现取Ⅰ组中No.2正解数值，代入式(29)，取yb>y，则逆解组数减少为16，其中，求得一组输入角θ1=62.185 4°，θ2=128.454 3°，θ3=134.557 2°，θ4=47.626 9°，其所对应的装配构型如图3b所示，这和已知的Ⅰ组的4个输入角一致，即图3a、图3b所示的为同一个构型，证明了正逆解的正确性。

(a)俯视图

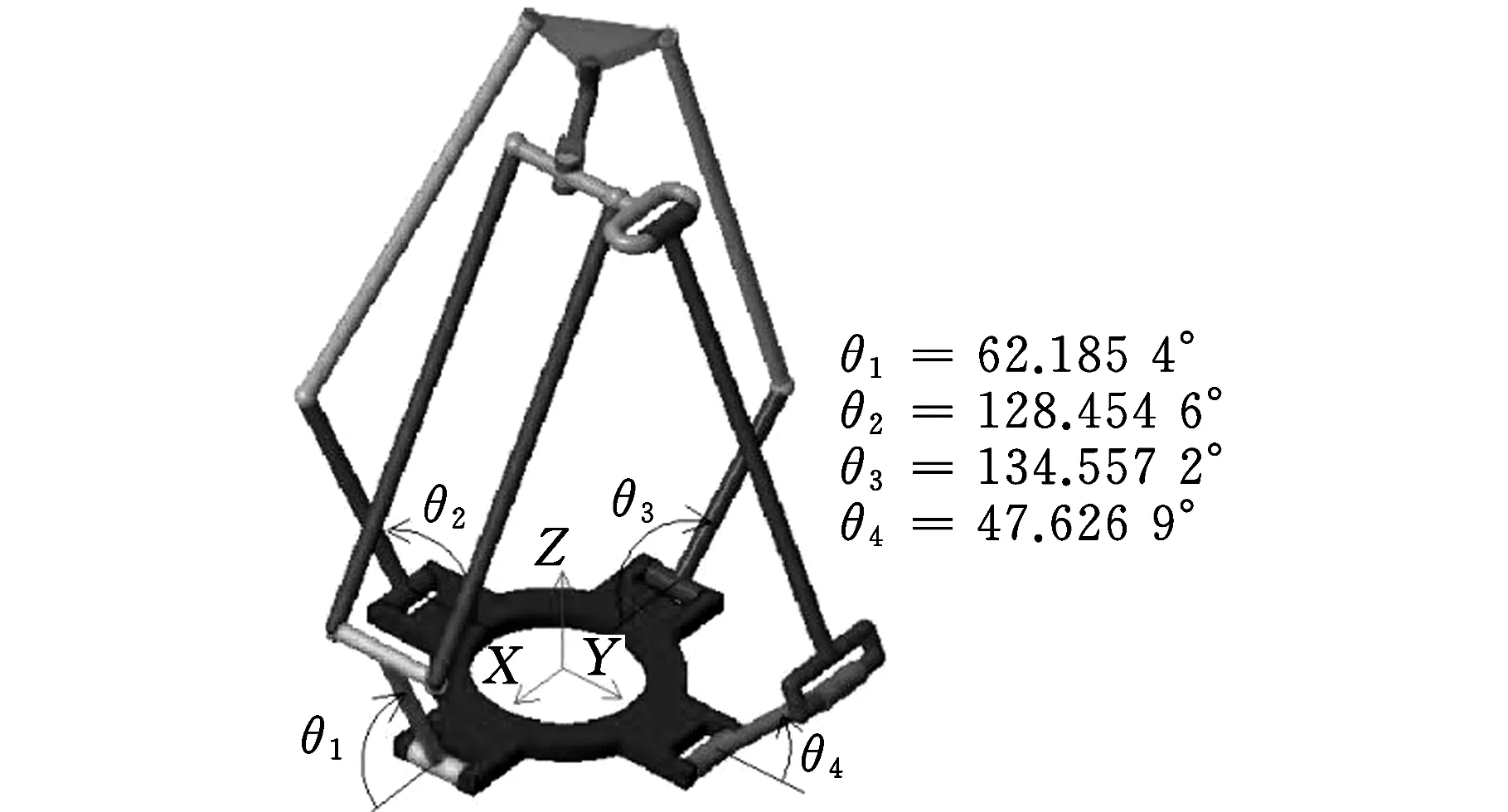
(b)三维立体图图3 Ⅰ组No.2正解所对应的装配构型Fig.3 Configuration for the solution No.2 of group Ⅰ

3 机构工作空间和动平台转角分析

3.1 基点工作空间分析

并联机构的基点工作空间即为末端执行器的工作区域，其大小是衡量并联机构性能的一个重要指标。本文采用极限边界搜索法[22]来分析该并联机构拓扑结构的工作空间，即预先设定该机构工作空间的Z向角度范围，通过改变搜索半径ρ、搜索角度θ来找到工作空间的边界。

先将搜索范围限制在：400 mm≤z≤1 200 mm， -π≤θ≤π，0≤ρ≤300 mm；运用MATLAB软件编程，得到机构工作空间的三维立体图(图4)，图5为不同高度z处的X-Y截面图。

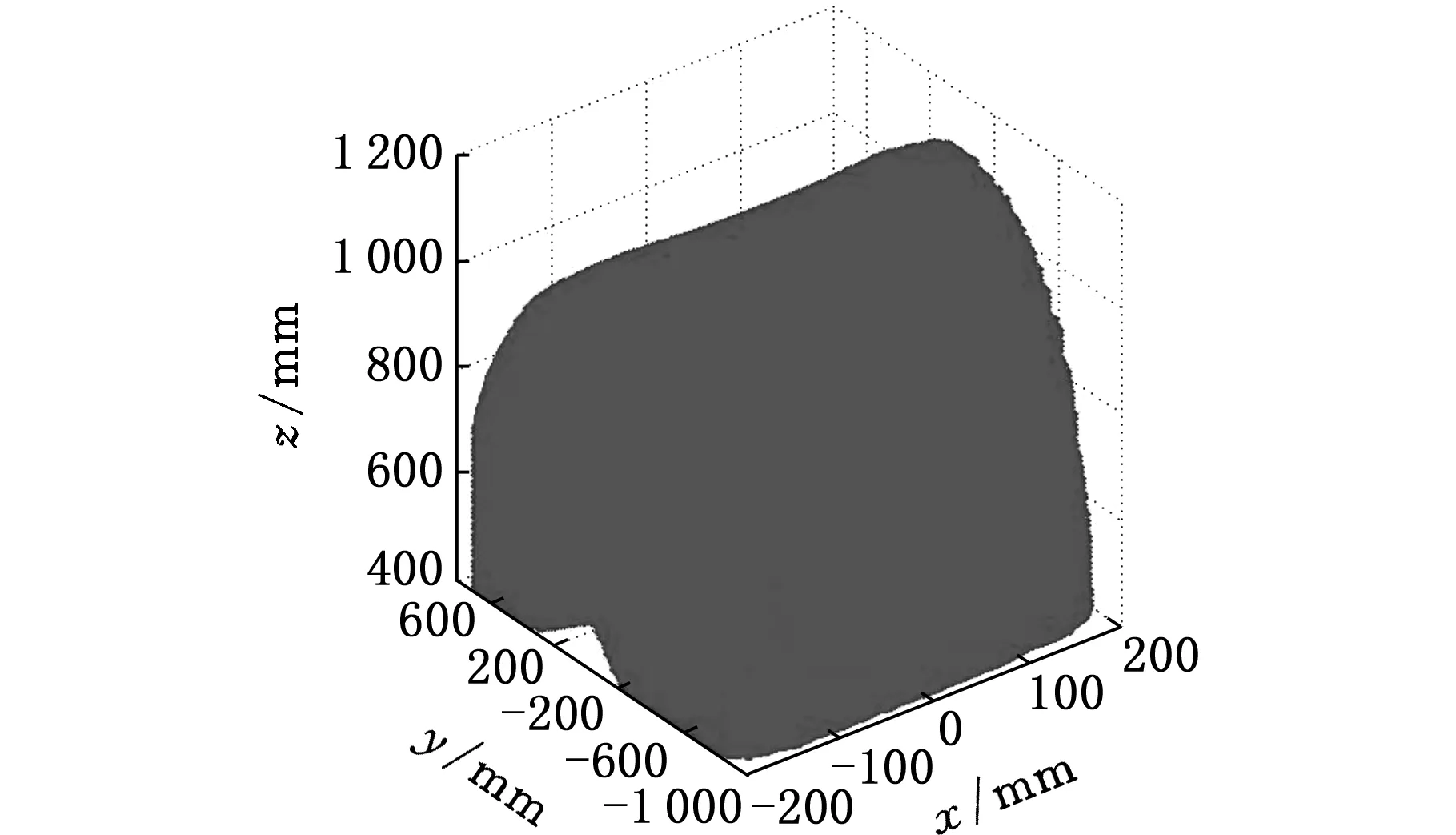
图4 机构工作空间的三维立体图Fig.4 3D workspace of the PM

由图4、图5可以看出：

①400 mm≤z≤500 mm时，该机构工作空间截面不连续；

②500 mm≤z≤1 150 mm时，该机构工作空间呈较规则的连续截面，且具有较好的对称性，但随着z的增加，其截面面积逐渐减小；

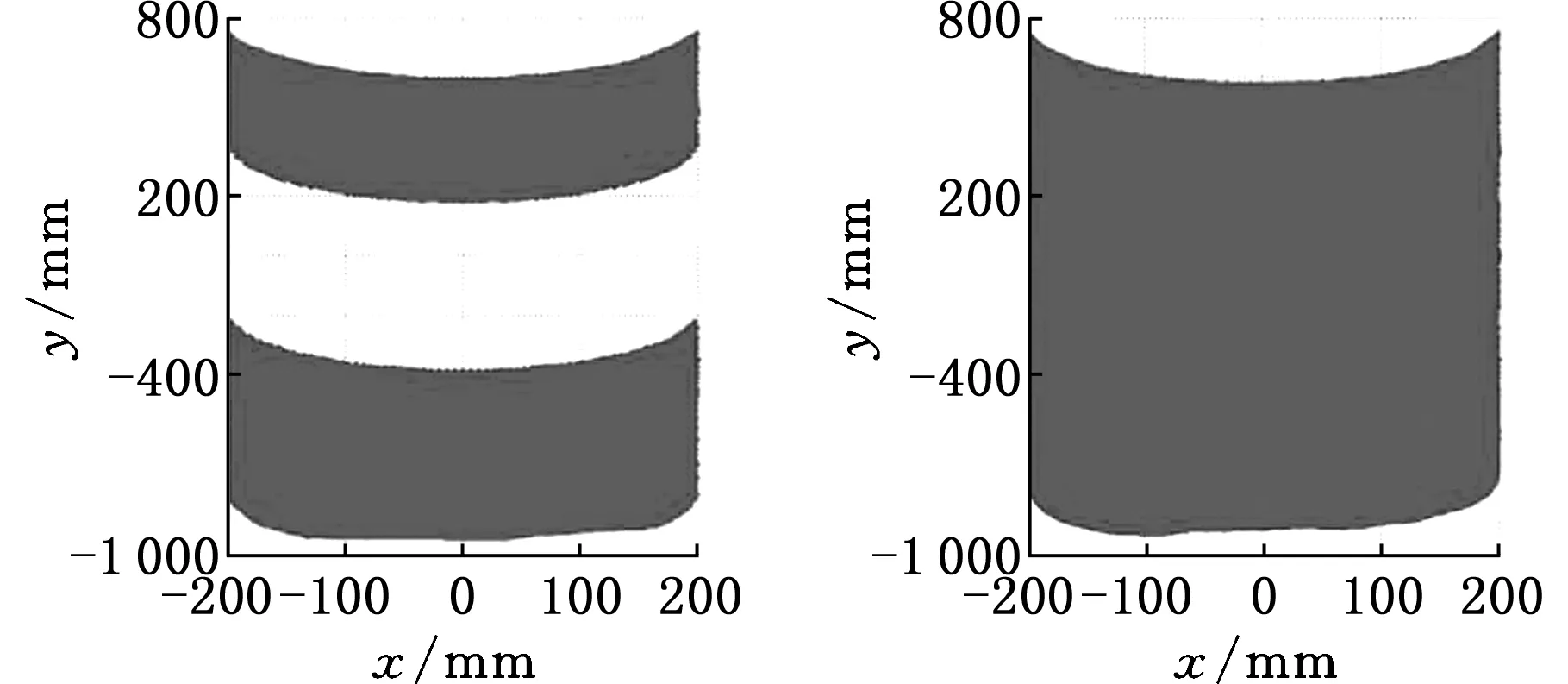
(a)z=400 mm(b) z=500 mm

(c)z=800 mm(d)z=1 000 mm图5 机构工作空间的X-Y截面图Fig.5 Cross-section of the workspace

③由于转动副R12只能在x=0的OYZ平面上移动，动平台上P点在X方向的两个极限位置完全取决于杆cR12的长度，因此，-200 mm≤x≤200 mm。

3.2 机构动平台转角分析

动平台转角分析在实际应用中具有重要意义[23]。对于并联机构，动平台基点处于工作空间内某一位置时，动平台的姿态角存在一定范围。根据逆解方程，采用极限边界搜索法，可求出基点处于工作空间内任一点时的转角范围。现取z=800 mm，基于MATLAB，计算该机构在工作空间内OXY平面上最小值αmin、最大值αmax的分布如图6所示。

图6中，区域A、B为工作空间内的同一个区域(z=800 mm)。由图6a可知，区域A内各点的转角的最小值均为-180°，由图6b可知，区域B内各点的转角的最大值均为180°，即动平台基点在该区域内的转角范围为[-180°,180°]，且该区域面积约为0.352 m2，约占该层工作空间截面总面积0.494 m2的72%，因此，在z=800 mm的平面内，该机构具有很好的转动能力。同样，可计算出其他不同高度z处的X-Y截面上各点处转角范围，发现该机构也具有很好的转动能力。

(a) αmin的分布

(b)αmax的分布图6 z=800 mm时机构工作空间内各点的转角能力Fig.6 Rotation capability of any point inside workspace when z=800 mm

4 奇异性分析

4.1 雅可比矩阵

式(25)～式(28)两边同时对时间t求导，得

(30)

i=1,2,3,4

JpV=Jqω

(31)

Jq=diag(u11,u22,u33,u44)

依据Jp、Jq矩阵是否奇异，将机构的奇异位形分为如下三类：①detJq=0时，机构发生输入奇异；②detJp=0时，机构发生输出奇异；③detJp=detJq=0时，机构发生综合奇异。

4.2 奇异性分析

4.2.1输入奇异

当机构发生输入奇异时，机构的执行构件将失去某个方向的运动能力，则至少有一个运动链到达了工作空间的边界。此时满足detJq=0，方程解的集合G为

G={G1∪G2∪G3∪G4}

(32)

G1={(za-zb)cosθ1+xasinθ1=0}，即R11、a、b三点在OXZ平面上投影共线；

G2={(zS22-zS23)cosθ2-(yS22-yS23)sinθ2=0}，即R21、S22、S23三点在OYZ平面上投影共线；

G3={(zS32-zS33)cosθ3-(xS32-xS33)sinθ3=0}，即R31、S32、S33三点在OXZ平面上投影共线；

G4={(zR42-zR43)cosθ4-(yR42-yR43)sinθ4=0}，即R41、R42、R43三点共线；

满足G1的三维CAD构型如图7所示。

图7 输入奇异位形Fig.7 Configurationof input singularity

4.2.2输出奇异

在输出奇异的情况下，当所有的主动件锁住时，执行构件依旧可以产生局部运动。此时，若机构末端执行器上作用有限的力，那么主动件上将需无穷大的驱动力才能达到力平衡。设：

(fi1,fi2,fi3)=ei

(33)

(fj1,fj2,fj3,fj4)=Ej

(34)

(1)2个向量线性相关。若ke1=e2，取k[f12f13]=[f22f23]，即向量S22S23和ab在OYZ平面上的投影平行，则

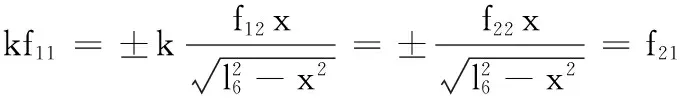
即向量S22S23在OXY平面上的投影、cR12和R13S33相互平行，其三维CAD模型如图8所示。e1和e3、e2和e4、e3和e4线性相关的条件与之相似(略)。

图8 输出奇异位形举例①Fig.8 Example ① of the configuration of output singularity

若e1=ke4，取[f12f13]=k[f42f43]，即向量S42S43和ab在OYZ平面上的投影平行，则

其三维CAD模型如图9所示。

图9 输出奇异位形举例②Fig.9 Example ② of the configuration of output singularity

若e2=ke3，即[f21f22f23]=k[f31f32f33]，则

kf34=k(f31l2sinα-f32l2cosα)=f21l2sinα-
f22l2cosα=f22l2sinα+f21l2cosα

即f21(sinα-cosα)=f22(sinα+cosα)，由于向量S22S23和S32S33平行且相等，故zS22=zS32且S22S32‖S23S33。根据R21S22=R31S32，得向量S23S33与X轴正方向的转角为135°，则

f21=-f22

(35)

即向量S23S23在OXY平面上的投影与X轴正向的转角为135°。则S22、S23、S33、S32四点在OXY平面上的投影共线，其三维CAD模型如图10所示。

图10 输出奇异位形举例③Fig.10 Example ③ of the configuration of output singularity

(2)3个向量线性相关。若e2=k1e1+k2e4(k1k2≠0)，取

则

即向量S22S23在OXY平面上的投影、cR12和R13S33相互平行且向量S22S23、ab、S32S33在OYZ平面上的投影均不平行。只要向量S22S23在OXY平面上的投影、cR12和R13S33相互平行，则机构发生输出奇异。同理可得其他情况成立的条件。

(3)4个向量线性相关。若向量e1、e2、e3、e4线性相关，则有

e1=k1e2+k2e3+k3e4k1k2k3≠0

由第(2)种情况分析方法，可以很快得出该种情况不成立。

4.2.3综合奇异

当机构发生综合奇异时，雅可比矩阵满足detJp=detJq=0，即输入奇异和输出奇异同时发生。例如：机构满足R21、S22、S23三点在OYZ平面上投影共线且向量S22S23在OXY平面上的投影、cR12和R13S33相互平行，其三维CAD构型如图11所示。

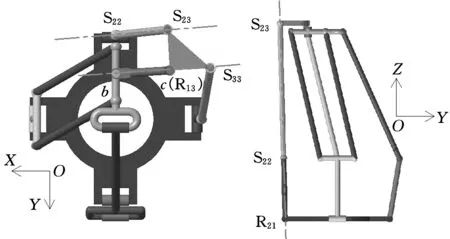
图11 综合奇异位形Fig.11 Configuration of mixed singularity

5 结论

(1)根据基于序单开链运动学建模原理，给出了机构位置正解的封闭方程，并求得其全部位置正解。

(2) 基于位置反解，对机构工作空间进行了分析，结果表明：z∈[500 mm,1 150 mm]时，该机构具有较规则的对称连续工作空间；工作空间X方向上的两个极限位置完全取决于杆cR12的长度。

(3)机构动平台绕其法线的整体转动能力很强，为该机构一个较突出的优点。

(4) 基于机构的位置反解，求解了该机构的雅可比矩阵，得到了该机构三种奇异位形发生的条件及其位置。

参考文献：

[1] YEN P L，LAI C H.Dynamic Modeling and Control of a 3-DOF Cartesian Parallel Manipulator[J]. Mechatronics, 2009，19(3):390-398.

[2] 张志胜，郑建勇，史金飞，等.一种运动解耦的XY向精密定位平台，中国：101556933A[P]. 2009-10-14.

ZHANG Zhisheng，ZHEN Jianyong，SHI Jinfei，et al. A Motion DecouplingXYPositioning Platform， China: 101556933A[P]. 2009-10-14.

[3] 童幸，高峰，张勇. 操作机主运动机构的解耦性研究[J].机械工程学报，2010，46(11)：14-20.

TONG Xing，GAO Feng，ZHANG Yong. Research on Decoupling Performance of Major-motion Mechanism for Forging Manipulators[J]. Journal of Mechanical Engineering，2010，46(11)：14-20.

[4] 石志新，罗玉峰，叶梅燕. 一类新型5自由度解耦并联机器人机构及位置分析[J].机床与液压，2010，38(17)：5-7.

SHI Zhixin，LUO Yufeng，YE Meiyan. Configuration Design and Displacement Analysis for a Class of Novel Fully Decoupling 5-DOF Parallel Manipulators [J]. Machine Tool & Hydraulics，2010，38(17)：5-7.

[5] ALTUZARRA O，LOIZAGA M，PINTO C，et al. Synthesis of Partially Decoupled Multi-level Manipulators with Lower Mobility[J]. Mechanism & Machine Theory，2010，45(1):106-118.

[6] GLAZUNOV V.Design of Decoupled Parallel Manipulators by Means of the Theory of Screws[J]. Mechanism & Machine Theory，2010，45(2)：239-250.

[7] 张帆，张丹.基于支链驱动理论的解耦球面转动并联机构型综合[J].农业机械学报，2011，42(11)：195-199.

ZHANG Fan，ZHANG Dan.Structural Synthesis of Decoupled Spherical Parallel Mechanism Based on Driven-chain Principle[J]. Transactions of the Chinese Society for Agricultural Machinery，2011，42(11)：195-199.

[8] LEGNANI G，FASSI I，GIBERTI H，et al.A New Isotropic and Decoupled 6-DoF Parallel Manipulator[J]. Mechanism & Machine Theory，2012，58(3)：64-81.

[9] 窦玉超，曾达幸，李明洋，等.一种两转一移完全解耦并联机器人机构及其特性分析[J].中国机械工程，2014，25(2)：241-245.

DOU Yuchao，ZENG Daxing，LI Mingyang，et al. Analysis of a 2T1R Fully Decoupled Parallel Robot Mechanism and Its Characteristics[J].China Mechanical Engineering，2014，25(2)：241-245.

[10] 沈惠平，熊坤，孟庆梅，等.并联机构运动解耦设计方法及其应用[J].农业机械学报，2016，47(6)：348-356.

SHEN Huiping，XIONG Kun，MENG Qingmei，et al. Design Methods for Kinematic Decoupled Parallel Mechanisms and Applications[J]. Transactions of the Chinese Society for Agricultural Machinery，2016，47(6)：348-356.

[11] KRUT S，NABAT V，PIERROT F. Heli4: A Parallel Robot for Scara Motions with a Very Compact Traveling Plate and a Symmetrical Design[C]//2006 IEEE/RSJ International Conference on Intelligent Robots and Systems. Beijing，2006：1656-1661.

[12] GOGU G.Structural Synthesis of Fully-isotropic Parallel Robots with Schönflies Motions via Theory of Linear Transformations and Evolutionary Morphology [J]. European Journal of Mechanics-A/Solids，2007，26 (2)：242-269.

[13] 罗玉峰，刘卓，石志新，等.三平移一转动并联机构型综合及分类[J].机械设计与研究，2010，26(5)：40-43.

LUO Yufeng，LIU Zhuo，SHI Zhixin，et al.Structural Synthesis and Classification of 3-translational and 1-rotation Parallel Manipulator[J].Machine Design and Research，2010，26(5)：40-43.

[14] XIE F，LI T，LIU X.Type Synthesis of 4-DOF Parallel Kinematic Mechanisms Based on Grassmann Line Geometry and Atlas Method[J]. Chinese Journal of Mechanical Engineering，2013，26(6)：1073-1081.

[15] LI Zhibin，LOU Yunjiang，ZHANG Yongsheng，et al. Type Synthesis, Kinematic Analysis, and Optimal Design of a Novel Class of Schönflies-Motion Parallel Manipulators [J]. IEEE Transactions on Automation Science & Engineering，2013，10(3)：674-686.

[16] 杨廷力，刘安心，罗玉峰，等.机器人机构拓扑结构设计[M].北京：科学出版社，2012.

YANG Tingli，LIU Anxin，LUO Yufeng，et al. Theory and Application of Robot Mechanism Topology[M]. Beijing：Science Press，2012.

[17] 沈惠平，杨廷力，孟庆梅，等.一种三平移一转动并联机器人平台装置,中国：201610403796.4[P]. 2016-6-8.

SHEN Huiping，YANG Tingli，MENG Qingmei，et al. A Three Translation and One Rotation Parallel Robot Platform Device, China: 201610403796.4[P]. 2016-6-8.

[18] YANG Tingli，LIU Anxin，SHEN Huiping，et al. Topology Design of Robot Mechanisms[M]. Singapore: Springer Publishing Company，2018.

[19] 沈惠平，尹洪波，王振，等.基于拓扑结构分析的求解6-SPS并联机构位置正解的研究[J].机械工程学报，2013，49(21)：70-80.

SHEN Huiping，YIN Hongbo，WANG Zhen，et al. Research on Forward Position Solutions for 6-SPS Parallel Mechanisms Based on Topology Structure Analysis[J]. Journal of Mechanical Engineering，2013，49(21)： 70-80.

[20] 沈惠平.基于序单开链法建模的代数法求解机构位姿[R].常州：常州大学现代机构学研究中心，2016.

SHEN Huiping.The Solution of Mechanism Based on the Ordered SOCS Modeling Method[R]. Changzhou： Center for Modern Institutional Studies，Changzhou University，2016.

[21] 刘平松.I4R型并联机器人全域性能及其优化研究[D].南京：南京理工大学，2013.

LIU Pingsong.Global Performance and Optimization of I4R Parallel Robot[D].Nanjing：Nanjing University of Science and Technology，2013.

[22] 黄真，孔令富，方跃法.并联机器人机构学理论及控制[M].北京：机械工业出版社，1997.

HUANG Zhen， KONG Lingfu， FANG Yuefa.Parallel Robot Mechanism Theory & Control[M].Beijing：China Machine Press，1997.

[23] XIE Fugui，LIU XinJun. Design and Development of a High-speed and High-rotation Robot with Four Identical Arms and a Single Platform[J].Mechanisms and Robotics，2015，7 (4)：041015.