废旧汽车再制造逆向物流网络模型优化

董贵颖 胡坚堃 黄有方

摘要：

针对市场对汽车再制造产品的需求不确定和再制造设施投入成本高的问题，引入多等级设施、市场需求率和回收率，通过对废旧汽车再制造逆向物流网络涉及到的各项成本和收入进行权衡，建立一个以收益最大为目标的混合整数规划模型，并用离散粒子群优化算法对模型进行求解，确定再制造物流网络中各设施的数量、位置和等级，以及各设施间的物流量分配。对市场需求率、回收率、设施能力等参数进行灵敏度分析，研究各参数对网络模型的影响。通过仿真实例验证模型和算法的有效性。

关键词：

再制造物流; 逆向物流; 网络设计; 设施能力; 市场需求; 离散粒子群优化（DPSO）算法

中图分类号： F253.9

文献标志码： A

Model optimization of end-of-life automobile

remanufacturing reverse logistics network

DONG Guiying， HU Jiankun， HUANG Youfang

（

Institute of Logistics Science & Engineering， Shanghai Maritime University， Shanghai 201306， China）

Abstract：

In view of the uncertain market demand of automobile remanufactured products and the high cost of remanufacturing facilities， introducing the multi-grade facilities， the market demand rate and the recovery rate， considering each cost and revenue in the reverse logistics network of end-of-life automobile remanufacturing， a mixed integer programming model with the objective of maximizing profit is constructed. The discrete particle swarm optimization （DPSO） algorithm is used to solve the model. The number， location and grade of the facilities in the remanufacturing reverse logistics network and the flow distribution among the facilities are determined. The sensitivity analysis on the market demand rate， the recovery rate and the facility capacity is given， and their influence on the network model is studied. Through simulating an instance， the validity of the model and the algorithm is verified.

Key words：

remanufacturing logistics; reverse logistics; network design; facility capacity; market demand;discrete particle swarm optimization （DPSO） algorithm

收稿日期： 2017-03-28

修回日期： 2017-11-08

基金项目：

国家自然科学基金（41505001）;上海市科学技术委员会科研计划（14DZ2280200）

作者简介：

董贵颖 （1991—），女，河北保定人，硕士研究生，研究方向為物流管理与工程，（E-mail）1947698465@qq.com;

胡坚堃（1983—），男，浙江绍兴人，工程师，研究方向为航运物流，（E-mail）jkhu@shmtu.edu.cn;

黄有方（1959—），男，浙江新昌人，教授，博导，博士，研究方向为物流管理与工程，（E-mail）yhuang@shmtu.edu.cn

0 引 言

近年来，随着我国制造业的发展，能源短缺和环境污染问题日益严重，废旧产品大量堆积。再制造物流因其可以回收再利用废旧产品的价值，成为研究的热点。汽车产业作为我国经济发展的支柱产业，其市场前景广阔并占据着大量资源。对废旧汽车进行再制造会为社会带来显著的环境效益和经济效益，但面临着市场对再制造产品需求的不确定和再制造设施投入成本高的问题，这限制了我国废旧汽车再制造业的发展，也限制了我国经济的发展。

目前，对再制造物流网络设施选址的研究已取得了不少成果[1-2]。网络设计是逆向物流系统的战略层决策[3]，网络一旦确定，就会长期影响整个物流系统的运作。梁碧云等[4]对废旧汽车的回收模式进行了总结，通过成本效益分析，为汽车企业的报废汽车逆向物流运作模式选择提供参考。DEMIREL等[5]提出了不同角色参与下的废旧汽车逆向物流网络，并对土耳其的废旧汽车数量和产生场景进行了分析。SEVAL等[6]在制造商负责其产品整个生命周期的背景下，建立了一个数学模型来管理报废车辆的逆向流动网络，用以确定网络设施的数量、位置以及物流量。ZAREI等[7]以运输成本和固定成本之和最小为目标建立再制造物流网络模型，并设计了遗传算法对模型进行求解。孙浩[8]考虑备选设施的规模问题，建立了单周期线性规划模型，提出了混合启发式算法对模型进行求解。徐友良等[9]以汽车再制造逆向物流网络为研究对象，以成本最小化为目标建立逆向物流网络优化模型，并用遗传算法对模型进行求解。RAMEZANI等[10]引入政府对逆向物流的促进作用研究再制造物流选址模型。周向红等[11]研究了政府的不同策略对再制造逆向物流网络构建的影响，利用粒子群算法求解模型，并得出政府实施激励性补贴策略对逆向网络构建意义更大的结论。市场需求程度和回收率必然会影响废旧汽车再制造物流网络的构建，而已有文献很少考虑这些因素，结合多等级设施的再制造物流网络设计的文献则更少，因此本文建立相应模型并用离散粒子群优化算法进行求解。

1 模型构建

1.1 问题描述及假设

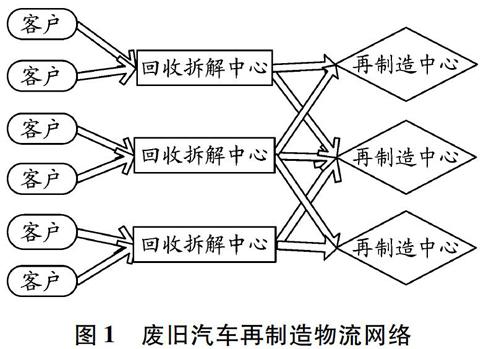
考虑一个由客户、回收拆解中心、再制造中心构成的废旧汽车再制造物流网络设计问题。首先废旧

汽车被送到回收拆解中心进行检测、分类暂存和拆解，然后有再利用价值的废旧零部件被运送到再制造中心进行加工再制造，见图1。经再制造中心加工的零部件可通过分销中心送至各消费区，用以满足顾客的需求。

图1

废旧汽车再制造物流网络

在建立模型前，给出以下几个假设：

（1）客户的废旧产品都先送往回收拆解中心，不会出现客户直接把废旧产品运送到再制造中心的情况;

（2）各客户区域拥有的废旧产品的数量已知;

（3）各回收拆解中心和再制造中心的备选地点已知，且各回收拆解中心和再制造中心分为不同等级，各等级中心所对应的固定成本和处理能力已知;

（4）市场对该类产品的需求量和对该类产品再制造件的需求率已知（企业通过统计调查和预测得到），在该产品的需求量中再制造产品可被接受的比例称为市场需求率;

（5）废旧产品的回收率未知，本文将回收拆解中心的实际回收量与最大可回收量的比称为回收率;

（6）废旧产品的废旧程度大致相同，单位废旧产品的处理成本（包括检测成本、拆解成本和再制造成本）已知，将单位废旧产品制成再制造产品能够带来的收益已知;

（7）运输成本与运输距离成正比。

1.2 模型参数与决策变量

1.2.1 模型参数

模型涉及的下标：

i為客户序号，i∈I，I为所有需要服务的客户集合;j为备选回收拆解中心的序号，j∈J，J为所有备选的回收拆解中心的集合;k为备选再制造中心的序号，k∈K，K为所有备选的再制造中心的集合;n是设施等级的序号，n∈N，N为所有设施等级的集合。

模型涉及的参数：ajn为n级回收拆解中心j的固定成本;akn为n级再制造中心k的固定成本;

h为单位废旧产品的处理成本;mjn为n级回收拆解中心j的最大处理能力;mkn为n级再制造中心k的最大处理能力;dij为客户i与回收拆解中心j之间的距离;dmax为客户与回收拆解中心之间允许的最大距离;djk为回收拆解中心j与再制造中心k之间的距离;g1为建造的回收拆解中心的最大数量;g2为建造的再制造中心的最大数量;cij为从客户i到回收拆解中心j的单位产品的单位距离运输成本;cjk为从回收拆解中心j到再制造中心k的单位产品的单位距离运输成本;αij为从客户i到回收拆解中心j的运输规模折扣率;αjk为从回收拆解中心j到再制造中心k的运输规模折扣率;μ为单位废旧产品再制造带来的收入;Qi为客户i拥有的废旧产品的数量;p1和p2为运输规模折扣的分界点;λ为废旧产品的回收率;D为市场需求量;β为市场对再制造产品的需求率;γ为回收率;M为一个很大的数。

1.2.2 决策变量

再制造逆向物流网络设计主要解决在哪些备选中心建立回收拆解中心和再制造中心，建立何种等级的回收拆解中心和再制造中心，以及各中心产品数量的问题。

决策变量分为0-1变量和实数变量两种。0-1变量包括：Zj，表示是否在备选地j建立回收拆解中心，如在备选地j建立回收拆解中心，则Zj=1，否则Zj=0;Zk，表示是否在备选地k建立再制造中心，如在备选地k建立再制造中心，则Zk=1，否则Zk=0;Yjn，表示是否在备选地j建立n级回收拆解中心，如在备选地j建立n级回收拆解中心，则Yjn=1，否则Yjn=0;Ykn，表示是否在备选地k建立n级再制造中心，如在备选地k建立n级再制造中心，则Ykn=1，否则Ykn=0。实数变量包括：xij，表示回收拆解中心j从客户i回收的废旧产品数量;xjk，表示从回收拆解中心j运到再制造中心k的废旧产品数量。

1.3 数学模型

1.3.1 目标函数

用再制造物流网络涉及的各项成本和销售收入构造收益函数，以收益最大作为目标函数。

C=

f

iQi，D，β，γ-

j

n（Yjnajn）+

k

n（Yknakn）+h

iQiλ+fα（xij）cij

i

j（xijdij）+

fα（xjk）cjk

j

k（xjkdjk）

（1）

式（1）的前一项表示销售收入函数，其取值与客户提供的废旧产品总量

Qi

，市场需求量D，市场需求率β和回收率γ有关，是分段函数。销售收入函数的取值公式为

fiQi，D，β，γ=

Dβμ，γ

iQi>Dβ

μγiQi，γ

Qi≤Dβ

式（1）的后一项表示各项成本，其中：第1项和第2项分别表示回收拆解中心和再制造中心的固定成本;第3项表示总处理成本;第4项和第5项分别表示从客户到回收拆解中心和从回收拆解中心到再制造中心的运输成本。fα（x）为运输规模折扣率函数，是分段函数，其取值与各中心之间的运输量有关。当各中心之间的运输量超过一定值时，对应的单位距离运输成本会得到相应折扣率，且运输量越大，折扣越优惠。fα（x）的取值公式为

fα（x）=

1，x≤q1

α1，q1<x<q2

α2，x≥q2

其中α2<α1<1。

1.3.2 约束条件

nYjn=Zj， j

（2）

nYkn=Zk， k

（3）

jxij≤Qi， i

（4）

ixij≤MZj， j

（5）

jxjk≤MZk， k

（6）

ixij=

kxjk， j

（7）

ixij≤mjnYjn， j，n

（8）

jxjk≤mknYkn， k，n

（9）

j n

Yjn≤g1， j，n

（10）

k n

Ykn≤g2， k，n

（11）

dijYjn≤dmax， i，j，n

（12）

xijxjk≥0

（13）

Zj，Zk，Yjn，Ykn∈{0，1}

（14）

式（2）和（3）确保不被选择的回收拆解中心和再制造中心的备选地不对应等级，被选择的回收拆解中心或再制造中心的备选地对应一个等级;式（4）确保从各客户回收的废旧产品数量不大于其供应量;式（5）和（6）防止不被选择的备选地接收废旧产品;式（7）确保流量平衡，即每个回收拆解中心的输入量等于输出量;式（8）和（9）确保回收拆解中心和再制造中心处理的废旧产品总量不超过其最大处理能力;式（10）和（11）分别为回收拆解中心和再制造中心的数量约束;式（12）保證从每个客户到建立的回收拆解中心的距离不超过距离的最大限制;式（13）确保决策变量xij和xjk的非负性;式（14）确保Zj，Zk，Yjn和Ykn为0-1变量。

2 粒子群优化算法求解

2.1 粒子群优化算法原理

在粒子群优化算法中，每个优化问题的潜在解都是一个粒子。所有粒子都有一个由被优化函数决定的适应度值和一个决定它们“飞行”方向、距离的速度。粒子追随当前的最优粒子在解空间中搜索，在每一次迭代中通过跟踪两个极值（一个是粒子本身找到的最优解，即个体极值Pbest;另一个是整个种群目前找到的最优解，即全局极值gbest）来更新自己。每个粒子会不断地进行比较和更新，当满足终止条件时停止更新并输出最优粒子。

2.2 离散粒子群优化算法求解过程

基于网络设计问题的离散粒子群优化算法的求解步骤如下：

（1）粒子的初始化。粒子的维度与候选地的数量有关，采用生成随机数方式产生粒子的初始位置。

如有8个回收拆解中心备选地、4个再制造中心备选地，则粒子的维度设为12，前8个位置代表回收拆解中心，后4个位置对应再制造中心。设置每个维度有n个等级，如[1，0，2，0，0，1，3，0，1，0，2，0]表示：选择回收拆解中心备选地1，3，6，7建立回收拆解中心，等级依次是1，2，1，3;选择再制造中心备选地1和3分别建立1级和2级再制造中心。选址策略确定后可进而求解各物流设施间的物流量分配。

（2）根据目标函数构造适应度函数，计算粒子的适应度值。为满足解的多样性，可以允许不符合约束条件的粒子产生，但其惩罚值很大。

（3）比较各粒子大小得到个体极值和全局极值。

（4）更新粒子。网络设计属于离散型问题，通过比较粒子与其个体极值Pbest和全局极值gbest对应位置的数值是否相同，以一定概率进行数值改变来进行更新，防止小数的产生。改变概率与迭代次数相关：迭代次数少时，改变概率大，使迭代前期满足解的多样性;迭代次数多时，改变概率小，使迭代后期的结果收敛。

（5）计算更新粒子的适应度值，更新个体极值Pbest和全局极值gbest。

（6）判断是否符合终止条件，满足则退出并输出结果，不满足则返回步骤（4）。

将离散粒子群优化算法的求解过程绘制成流程图，见图2。

图2

基于网络设计问题的离散粒子群优化算法流程

3 仿真实例及数值计算

本文中的备选回收拆解中心位置数据、备选再制造

中心位置数据和客户位置数据参考文献[7]中的实例数据，其他相关数据参考文献[12]中的实例数据，以保证数值的合理性。各备选回收拆解中心和各再制造中心的位置见表1。

表1

备选的回收拆解中心和再制造中心的位置

各客户的位置数据和废旧产品供应量数据见表2。

表2

客户位置及废旧产品供应量

再制造物流网络涉及的其他相关参数见表3。

表3

再制造物流网络的其他参数

设置市场需求率为0.6，回收率为0.8，用MATLAB对粒子群优化算法进行编程，求解仿真模型。迭代300次得到较优解，粒子为[3，0，2，1，0，3，1，0，0，2，2，0]，其对应的网络设计结果为：在回收拆解中心备选地1，3，4，6和7依次建立3级，2级，1级，3级和1级回收拆解中心，在再制造中心备选地2和3均建立2级再制造中心。从各客户到各回收拆解中心的运输量见表4，从各回收拆解中心到各再制造中心的运输量见表5。

此网络设计方案获得的最大收益为313万元，其中：销售收入8 000万元，处理成本4 800万元，固定成本2 000万元，总运输成本887万元。

表4

从各客户i到各回收拆解中心j的运输量

表5

从各回收拆解中心j到各再制造中心k的运输量

4 灵敏度分析

4.1 市场需求率和回收率

将市场需求率设置为低、中、高3个等级，其取值依次为0.3，0.5和0.7;将回收率也设置低、中、高3个等级，其取值依次为0.4，0.6和0.8;其他参数不变。研究9种情境下市场需求率和回收率对网络设计的影响，包括对收益、设施数量和规模的影响。

表6

9种情境下的最大收益

比较不同情境下的最大收益值，见表6。

从表6可以看出：当市场需求率低时，最大收益随着回收率的增加而减少;当市场需求率为中级时，最大收益随着回收率的增加先增加后减少;当市场需求率高时，最大收益会随着回收率的增加而增加。总之，当回收量小于再制造产品需求量时，收益会随着回收量的增加而增加，而当回收量超过再制造产品需求量后，因多余产品的投入无法转换为收入，收益反而会下降。因此，在不同市场需求率下，应以尽量多地满足再制造产品需求但不超过再制造产品需求的回收率为最优，此时获得最大收益。

图3

9种情境下的设施数量

比较不同情境下的回收拆解中心和再制造中心的数量，见图3。

从图3可以看出：市场需求率对设施数量并无直接影响，但在实际生活中，企业为获得较大收益，会根据市场需求率制定回收率，即市场需求率影响回收率，进而影响设施数量;回收率对设施数量的影响较大，随着回收率的增加，回收拆解中心的数量增加，再制造中心的数量先增加后基本稳定。

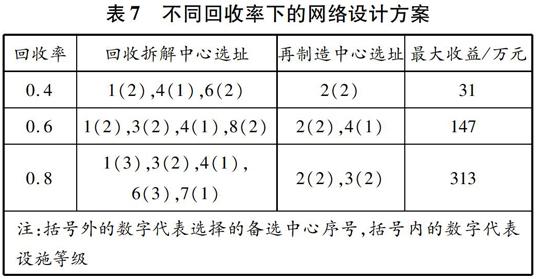
进一步研究回收率对设施规模的影响，将市场需求率设置为0.7，不同回收率下的网络设计方案见表7。

从表7中可以看出，回收率对再制造物流网络设计的影响不只表现在设施数量上，对设施规模也有影响。当回收率较低时，网络设计偏向于选择小型设施。当回收率高时，网络设计偏向于选择大型设施，虽然固定成本增加，但容易获得运输规模效益，整体上企业能够获得较大收益。

表7

不同回收率下的网络设计方案

4.2 设施能力

对回收拆解中心和再制造中心的设施能力进行

灵敏度分析，研究其对网络设计的影响。设置基本设施能力、设施能力提升20%、设施能力提升40%和设施能力缩减20%等4种情况，得到不同设施能力下再制造物流网络的最大收益，见图4。

从图4中可以看出，随着回收拆解中心或再制造中心设施能力的提高，再制造物流网络的最大收益也在提高。

图4

不同设施能力下再制造

物流网络的最大收益

进一步研究设施能力对设施数量和规模的影响，不同设施能力下的再制造物流网絡设计方案见表8。

从表8可以看出，随着设施能力的增加，再制造物流网络设计方案中不是设施数量减少就是设施规模降低，固定成本减少，因而最大收益提高。

表8

不同设施能力下的再制造物流网络设计方案

4.3 单位运输成本

对从客户到回收拆解中心的单位运输成本（C1 ）和从回收拆解中心到再制造中心的单位运输成本（C2 ）进行灵敏度分析，设置基本运输成本、高运输成本（运输成本提高100%）和低运输成本（运输成本降低50%）等3种情况。不同单位运输成本下的再制造物流网络设计方案见表9。

从表9可以看出：C1和C2的减少都会增加收益值，但C1对收益的影响比C2对收益的影响更大;

随着

C1的增加，

表9

不同单位运输成本下的再制造物流网络设计方案

设施数量和规模基本不发生变化，而随着

C2的变化，设施数量和规模会发生较小的变化。因此，单位

运输成本对设施数量和规模的影响并不大。

5 结 论

考虑废旧汽车再制造物流涉及的固定成本、运输成本、处理成本和销售收入，以收益最大为目标，建立一个再制造逆向物流网络模型。通过引入多等级设施，实现网络设计的整体优化，并用离散粒子群优化算法对模型进行求解。通过MATLAB编程计算确定了再制造物流网络中各设施的数量、位置和等级，以及各设施间的物流量分配。通过仿真实例，验证了模型和算法的有效性。

通过对市场需求率和回收率进行灵敏度分析，发现市场需求率对收益有较大影响，在不同市场需求率下要使再制造物流网络获得最大收益，应以尽量满足再制造产品需求但不超过再制造产品需求的回收率为最优。市场需求率通过影响回收率间接影响网络设计的设施数量和规模：随着回收率的增加，设施数量增加，设施规模由小型逐渐向大型转化。

通过对设施能力和单位运输成本进行灵敏度分析发现，设施能力会影响再制造物流网络的收益、设施数量和规模，而单位运输成本只影响再制造物流网络的收益。

参考文献：

[1]

POKHAREL S， MUTHA A. Perspectives in reverse logistics： a review[J]. Resources， Conservation and Recycling， 2009， 53（4）： 175-182.

[2]ALUMUR S A， NICKEL S， SALDANHA-DA-GAMA F， et al. Multi-period reverse logistics network design[J]. European Journal of Operational Research， 2012， 220： 67-78.

[3]LAMBERT S， RIOPEL D， ABDUL-KADER W. A reverse logistics decisions conceptual framework[J]. Computers & Industrial Engineering， 2011， 61（3）： 561-581.

[4]梁碧云， 丁宝红， 施俊才. 废旧汽车逆向物流回收模式决策分析[J]. 物流技术， 2013， 11（21）： 199-204.DOI： 10.3969/j.issn.1005-152X.2013.11.063.

[5]DEMIREL E， DEMIREL N， GKEN H. A mixed integer linear programming model to optimize reverse logistics activities of end-of-life vehicles in Turkey[J]. Journal of Cleaner Production， 2014， 41： 1-13.

[6]SEVAL E， ZTRK N. Network modeling for reverse flows of end-of-life vehicles[J]. Waste Management， 2015， 38（3）： 284-296.

[7]ZAREI M， MANSOUR S， KASHAN A H. Designing a reverse logistics network for end-of-life vehicles recovery[J]. Mathematical Problems in Engineering， 2010， 36： 1-16. DOI： 10.1155/2010/649028.

[8]孫浩. 制造/再制造集成物流网络设施选址模型及算法[J]. 工业工程与管理， 2009， 14（3）： 70-77.

[9]徐友良， 陈锦生， 石悦悦. 汽车再制造逆向物流网络选址规划研究[J]. 公路交通科技， 2015， 32（9）： 154-158. DOI： 10.3969/j.issn.1002-0268.2015.09.026.

[10]RAMEZANI M， BASHIRI M， TAVAKKOLI-MOGHADDAM R. A new multi-objective stochastic model for a forward/reverse logistic network design with responsiveness and quality level[J]. Applied Mathematical Modelling， 2013， 37（2）： 328-344.

[11]周向红， 高阳， 任剑. 政府补贴下的再制造逆向物流多目标选址模型及算法[J]. 系统工程理论与实践， 2015， 35（8）： 1996-2003.

[12]李强. 废旧汽车逆向物流运作模式的选择与网络构建研究[D]. 无锡： 江南大学， 2016.