交流电机硬线圈及其梯形梭绕设计

李训虎，管 风，卢 彬

(成都中车电机有限公司，成都 610051)

0 引 言

线圈是电机的关键部件，其尺寸设计合理与否，不仅直接影响嵌线的难易程度，而且对电机的使用寿命与运行可靠性有至关重要的影响。目前，对硬线圈尺寸的确定主要有作图法[1-2]、公式法[3-5]。作图法虽可满足工程应用，但较为繁琐，速度慢，且易出错；公式法根据硬线圈的空间几何结构，推导相应计算公式，便于编程处理。但现有公式法粗略认为线圈上、下层边在定子内圆上的夹角为线圈在定子内圆上的夹角一半，且按圆柱面推导，从而导致线圈端部轴向长度计算不准确。此外，上述现有方法在计算中均做了较多简化，导致参数计算结果误差较大，且均是针对跑道形梭绕线圈，与线圈实际拓扑结构不同。

鉴于现有方法的不足，本文针对实际设计需求，以硬线圈几何拓扑结构为基础，在充分考虑其空间几何结构的基础上，准确推导了其尺寸计算公式，并推导了其梯形梭绕尺寸计算公式。在此基础上，借助Visual Basic 6.0平台开发了相应的计算软件，并验证了其工程实用性。

1 线圈的空间拓扑结构

线圈的空间拓扑结构决定了线圈的计算方法。线圈主体由直线段、端部斜线段、鼻部构成，如图1(a)所示。在空间上，线圈上、下层边直线段中线轨迹为两个同心的圆筒；线圈上、下层端部斜线段中线轨迹为两个同心的圆锥，故其端部斜线段空间轨迹为锥面螺旋线；此外，圆筒与圆锥的中心与电机的中心重合。据此，硬线圈三维视图，如图1所示。

(a) 线圈主体

(b) 线圈实体模型

(c) 线圈端部斜线段轨迹

由图1可见，从线圈两个鼻部的中间将其分为上层部分与下层部分，由于中心相同而轨迹半径不同，故线圈上、下层边的长度不同。虽通过调整线圈鼻部的位置角度与偏转角度，可使其上、下层边长度基本相同，从而形成跑道形梭绕，如图2(a)所示。但该法在后续线圈涨型中需调整上、下层边的涨型角度，不便于涨型。为避免上述问题，可采用图2(b)所示梯形梭绕。

(a) 跑道形梭绕

(b) 梯形梭绕

2 线圈设计的要素

交流电机线圈设计主要考虑两个要素：端部嵌线间隙/端部轴向长度、单匝长度。

由于线圈直线段长度基本由电机的电磁计算确定，因此线圈端部轴向长度是决定电机轴向长度的关键因素。从线圈的空间结构可知，端部嵌线间隙决定了端部轴向长度，且其对电机端部的散热能力有较大影响，尤其是对结构要求极其紧凑的机车牵引电机。因此，本设计方法中将端部嵌线间隙和轴向长度作为重要的调整参数和判据，并以0.1 mm的步长来调整。

线圈单匝长度是工艺和成本的重要参考量，其数值越准确越好。现有方法未考虑线圈直线段弯端部及端部弯鼻部的弯曲半径对线圈单匝长的影响，算法也比较简化，其计算结果和实物误差较大。为提高计算精度，本设计方法采用空间曲线和精确的分段计算法。

3 硬线圈计算公式推导

针对硬线圈的结构特点，在充分考虑其空间几何结构的基础上，本文准确推导了其尺寸计算公式。但限于篇幅，本文仅给出与现有公式法的不同之处。

(1) 锥面螺旋线的处理

对硬线圈而言，由于嵌线完成后端部呈喇叭口型，故线圈端部为锥面螺旋线，如图1(b)、图1(c)所示。因此，精确计算线圈端部长度需采用积分法，但该法较为复杂，且占用较多计算资源，故本文在保证锥面螺旋线长度不变的情况下，将圆锥等效为圆柱，并采用圆柱螺旋线的方法计算线圈端部长度。即：

(1)

式中：D表示等效圆柱直径；D1，D2分别表示圆锥上、下底直径。

计算表明，与积分法相比，本方法计算误差随D1/D2减小而增加，但即便D1/D2=0.1，误差也仅为1%，故本方法满足工程精度要求。

(2) 端部轴向长度计算

由于线圈鼻子偏转，导致线圈上、下层边在定子内圆上的夹角小于线圈在定子内圆上夹角的一半。而现有公式法粗略认为线圈上、下层边在定子内圆上的夹角为线圈在定子内圆上夹角的一半，从而导致端部轴向长度计算不准确。为此，本文推导了硬线圈上、下层边在定子内圆上夹角的计算公式，以准确计算端部轴向长度。

硬线圈的端部视图，如图3所示。

图3 硬线圈端部视图

由图3可见，线圈上层边夹角α1与下层边夹角α2分别：

α1=0.5α-δ1

(2)

α2=0.5α-δ2

(3)

式中：α,δ1,δ2分别按式(4)～式(6)计算。

(4)

式中：yc表示节距；z1表示定子槽数。

(5)

式中：r1表示线圈上层边终止半径；r2表示线圈鼻子中心半径；β表示鼻子偏转角。

(6)

式中：r3表示线圈下层边终止半径。

线圈端部轴向长度lE计算公式如下：

(7)

式中：θ1表示线圈上层边升角，其值采用文献[1]的方法计算。

针对既有产品，分别采用现有公式法与本方法，计算所得线圈端部轴向长度和端部嵌线间隙，如表1所示。

表1 端部轴向长度和嵌线间隙计算结果对比

表1中,实值表示生产用图纸标注值，法1表示现有公式法，法2表示本方法。计算方法为设定端部轴向长度，计算端部嵌线间隙。由表1可知，两种方法计算值差异较大，本方法计算值更符合实际值。此外，通过大量实例计算表明，当嵌线间隙较小时，两种方法计算差异较小；当嵌线间隙较大时，本文的方法计算精度更高。

(1) 线圈单匝长计算

为便于嵌线及端部整形，硬线圈直线段至端部及端部至鼻部均有一定的弯曲弧度，如图4所示。现有公式法在计算线圈单匝长时以折线代替弯弧，导致计算精度降低。鉴于此，本文推导了计及弯曲弧度影响的线圈单匝长计算公式。

图4 线圈弯曲示意图

由于硬线圈上、下层边升角不同，应分别考虑弯曲弧度对线圈单匝长的影响，但其思路一致。因此，限于篇幅，本文仅给出计及弯曲弧度影响的线圈上层边长度计算公式的推导过程。

(8)

(9)

式中：r4表示直线段弯端部弯曲半径；r5表示端部弯鼻部弯曲半径。

(10)

(11)

因此，以折线代替弧长后需进行的补偿量计算:

(12)

(13)

基于此，硬线圈上层边长lc1按下式计算：

(14)

式中：lt表示铁心长；l5表示鼻部展开长。

此外，现有公式法认为线圈上、下层边长度一致。而对于硬线圈其上、下层边长度不一致，故本文分别进行计算。

针对既有产品，分别采用现有公式法与本方法计算线圈单匝长，结果如表2所示。

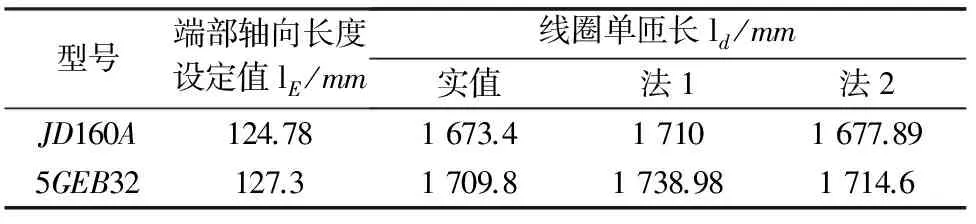
表2 线圈单匝长计算结果对比

由表2可知，现有方法与本文方法计算所得线圈单匝长差异明显，本文方法计算值与实际值更接近，精度更高。

(2) 梯形参数计算

由于现有公式法主要针对跑道形硬线圈，故无梯形参数计算。而对于梯形硬线圈而言，需计算梯形下底夹角度数、梯形高等参数。

梯形参数计算用图，如图5所示。

图5 梯形参数计算用图

对于梯形下底夹角度数的计算，本文采用迭代法，其流程如图6所示。

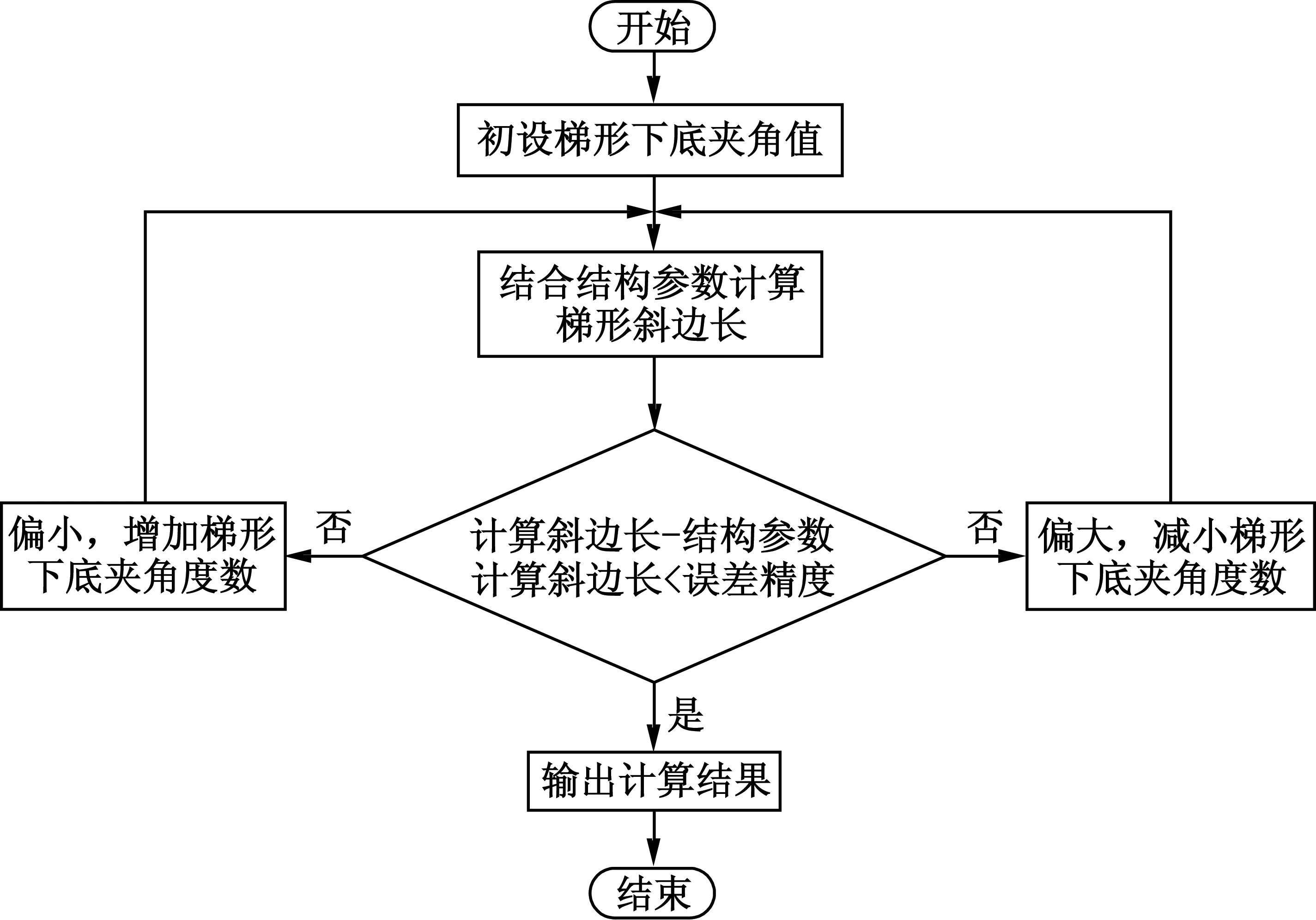
图6 梯形下底夹角度数计算流程

在计算出梯形下底夹角度数的基础上，本文采用分段方式对梯形高度进行计算。此外，为保证模具的通用性，设计时可以使梯形下底夹角度数、梯形上底倒角R及中线鼻部半径与现有模具相同，从而使用现有模具。同时，为避免二次弯形，梯形设计时梯形上底倒角R应不与线圈直线段弯斜线段的弯角重合。

4 验 证

在新产品设计时，采用本方法设计新线圈，计算参数如表3所示。

表3 采用本文方法计算新线圈

线圈制成后称其重量，并取1m同材料称其重量，二者相除得已制成线圈的长度。减去引线头的长度，再除以匝数，得单匝长度1 271.12mm。实际测量线圈轴向总长511mm。

按总长511mm重新计算线圈，参数如表4所示。

表4 重新计算线圈

由此可知，计算值和实测值基本吻合，从而验证了本方法的正确性。线圈嵌线后，其实物如图7所示，测量其端部嵌线间隙约为3.5mm，与计算值一致。

在推导了硬线圈尺寸计算公式的基础上，本文借助VisualBasic6.0平台，开发了相应的计算软件，其界面如图8所示。

图7 线圈端部实物

图8 硬线圈计算程序

5 结 语

本方法和计算程序在初步设计中，能快速有效地计算线圈各种参数，大大提高了线圈计算的时效，目前已在公司中推广，并获得了国家发明专利，在多款新产品设计中使用，计算结果和产品实物吻合。

[1] 湘潭电机厂.交流电机设计手册[M].长沙：湖南人民出版社，1978.

[2] 傅丰礼.异步电动机设计手册(第二版)[M].北京：机械工业出版社，2008.

[3] 成清和.交流电机双层硬绕组计算[J].中小型电机，1991，1：15-18.

[4] 朱福伦，薛国苓.三相异步电动机硬绕组定子线圈尺寸的计算方法[J].电机技术，1990，3：25-27.

[5] 刘田娥.转子硬绕组的设计计算[J].电机技术，2001，3：9-12.