基于响应曲面法优化永磁轮毂电机辅助槽尺寸的研究

李化影，李明明，迟长春，刘红松，籍海亮

(上海电机学院，上海 200240)

0 引 言

永磁轮毂电机由于定子齿槽的存在，导致气隙不均匀分布，气隙磁场随转子变化会引起电机的齿槽转矩[1]。在永磁电机低速轻载运行时，齿槽转矩较为明显，影响着电机的运行稳定性和性能；在永磁电机变速行驶时，当定转子的机械共振频率与转矩的脉动频率一致时，齿槽转矩产生的噪声及振动将被放大[2]。因此，在永磁轮毂电机的设计中，必须削弱电机的齿槽转矩。

目前，国内外专家学者对齿槽转矩的削弱进行了大量的研究，并取得了一定的研究成果。齿槽转矩的削弱方法主要有斜槽、采用不等宽槽口、定子开辅助凹槽及极槽配合等；斜槽法在实际工程应用中，增加了电机的加工制造难度，同时是以牺牲电机的电磁转矩为代价，实际很少使用；不等槽口宽法，槽口宽度的确定受导线线径、嵌线方式等因素影响，很难做到结构上槽口宽度的合理性；极槽配合法很难保证理论与实际极槽数相符合，且机械加工受很多实际因素的影响；而定子齿开辅助凹槽由于增加了永磁电机齿槽转矩的基波周期数，对原槽口的齿槽转矩起抵制作用[3]，只需改变定子齿的形状，就可以削弱永磁电机的齿槽转矩，结构简单可靠。因而，定子齿开辅助凹槽是抑制电机齿槽转矩较为可行的方法。文献[4-6]中分析了辅助槽槽型、尺寸及辅助槽个数对齿槽转矩的影响，并由分析结果可知辅助凹槽对齿槽转矩的削弱是有条件的，合适的辅助槽尺寸和个数可以有效地降低电机的齿槽转矩，反之会增大原来电机的齿槽转矩，且定子齿开矩形辅助槽对齿槽转矩的抑制效果最佳。文献[7]分析了对于单元电机槽数Z0为奇数的电机，辅助凹槽数Nn=2时，可明显削弱电机的齿槽转矩。

本文以54槽48极永磁无刷轮毂电机为例，所设计的单元电机模型Z0=9为奇数，由文献[7]知，开两个辅助凹槽可以显著减少电机的齿槽转矩，开一个或开3个辅助槽反而增大原来电机的齿槽转矩，故本文研究考虑开2个辅助凹槽时槽宽、槽深和槽中心线夹角对齿槽转矩的影响。

由于目前一些参考文献对于开辅助槽尺寸的选取，一般通过有限元法对辅助槽尺寸进行参数化仿真，通过齿槽转矩峰峰值的对比分析，再选取合适的辅助槽尺寸，此法对电脑运行速度要求高,计算精度难以保证，且很难保证同时运行时得到多变量之间的关系。本文提出了采用响应曲面法对辅助槽的槽宽b、槽深h及槽中心线夹角β尺寸进行最优化分析，运用Design-Expert软件对辅助槽尺寸三自变量值进行数据处理，进而得到最优辅助槽尺寸。

1 齿槽转矩的原理分析

齿槽转矩是当电机没通电时磁场能量W相对于位置角的α的负导数[8]，即：

(1)

在分析表贴式永磁无刷轮毂电机齿槽转矩时，通常认为定子铁心的磁导率无穷大，即μFe=，同一型号电机中永磁体的尺寸大小相同、性能参数相同，形状分布均匀；且永磁体的磁导率与空气相同。

式(1)中α为某一指定的齿中心线和永磁体磁极中心线的夹角，即定转子之间的相对位置角，其中θ=0在永磁体磁极的中心线上位置[9]。如图1所示。

图1 永磁体与电枢的相对位置图

假设电机内部存储能量近似为电机气隙与永磁体中的磁场能量[10]，即：

(2)

磁场能量W的大小与电机定转子相对位置、结构尺寸、及永磁体的性能紧密相关[11]。气隙磁密B与相对位置角α之间的关系近似表示：

(3)

式中：Br(θ)，hm(θ)，δ(θ,α)分别为永磁体剩磁、永磁体沿充磁方向长度、气隙有效长度。式(2)可表示：

(4)

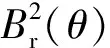
(5)

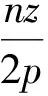
2 有限元设计

2.1 电机模型

本文借助Ansoft有限元仿真软件对54槽48极电机进行建模分析，电机的主要参数如表1所示。

表1 电机主要参数

为了便于分析，提高运算速度，取电机的1/6模型进行仿真。电机的分析模型如图2所示。

图2 轮毂电机的1/6模型图

2.2 定子齿开槽法

本文采用在定子齿开两个辅助矩形凹槽来分析齿槽转矩，其中b为辅助槽槽口宽，h为辅助槽槽深，β为两相邻辅助凹槽的中心线夹角。为避免不恰当的开辅助槽引进新的谐波，本文所开辅助凹槽均沿定子齿中心线严格对称。

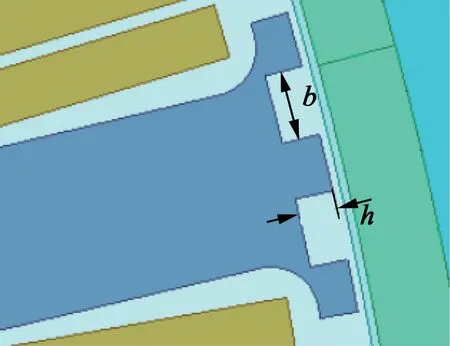
(a) 辅助槽口宽和槽口深

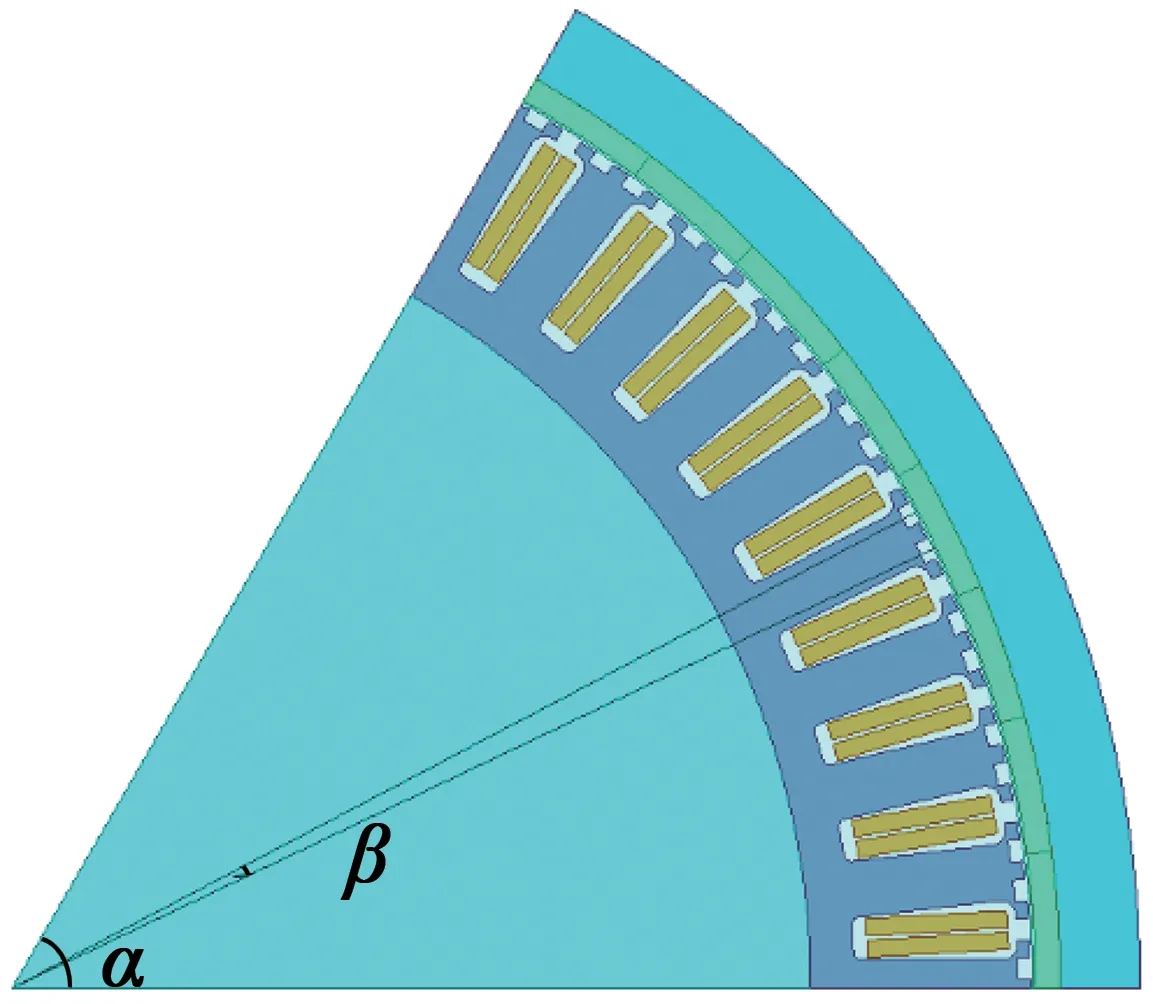
(b) 辅助槽中心线夹角

3 响应曲面法优化辅助凹槽尺寸

响应曲面法(RSM)是近年来优化永磁电机的一种方法，它是在合理试验设计方法的基础上得到的一组数据，采用多元二次回归方程拟合因素与响应值之间的函数关系，通过回归方程的分析来寻求最优工艺参数，解决多变量问题的一种统计方法[12]。即将体系的响应作为一个或多个因素函数的一种最优化方法，因素个数一般不超过4个，且因素均为计量值数据。

研究表明辅助槽尺寸的选取对齿槽转矩的抑制有着很大的影响，合理的辅助槽尺寸可以有效地削弱齿槽转矩。本文避免了采用常规有限元法仿真寻求辅助槽尺寸，而是通过响应曲面法对辅助槽的槽宽b、槽深h及槽中心线夹角β尺寸进行最优求解，进而得到最优辅助槽尺寸。

响应曲面法设计方法有很多，最常用的方法是BBD和CCDs法[13]。本文的轮毂电机，由于非线性因素的影响，自变量和响应之间的关系是未知的，且自变量之间是交互的，故采用二阶响应模型去求得合适的响应拟函数。本文采用BBD法，借助Design-Expert软件对辅助槽的槽宽b、槽深h及槽中心线夹角β三自变量进行数据处理，寻求最优辅助凹槽尺寸。

本文永磁轮毂电机的响应曲面模型考虑了交互效应和二次效应，且试验区域接近响应面的最优区域，故采用二阶模型去逼近：

(6)

式中：βi为xi的线性效应；βii为xi二次效应；βij为xixj之间的交互效应。

本文自变量的取值范围：1≤b≤3,0.2≤h≤1.5,1.5≤β≤3。

三自变量用x1，x2，x3来表示，其中thet即为β，齿槽转矩用y表示，利用Design-Expert软件设计求得二阶回归方程：

y=+10.511 20-0.311 94x1-

2.526 95x2-6.026 16x3-0.193 69x1x2+

0.140 47x1x3-0.795 44x2x3+

(7)

由二阶回归模型方程求解分析，如图4与图5所示。

图4 二阶回归模型的Rankit图

图5 回归模型方程曲线

由图4可以看出，顺序残差与期望值之间的关系接近线性关系，由此可知永磁轮毂电机的回归模型是合适有效的。同时由图5可知，辅助槽宽的尺寸对齿槽转矩的作用最不显著，变化极为平缓，而辅助槽深对齿槽转矩的变异度最大，槽中心线夹角类似，故可以通过改变槽深和槽中心夹角使齿槽转矩发生显著的变化。

同时可得到三变量之间的交互作用三维图，将其中一个自变量固定不变，得到另外两个自变量的交互作用对齿槽转矩影响曲面三维图，如图6～图8所示。

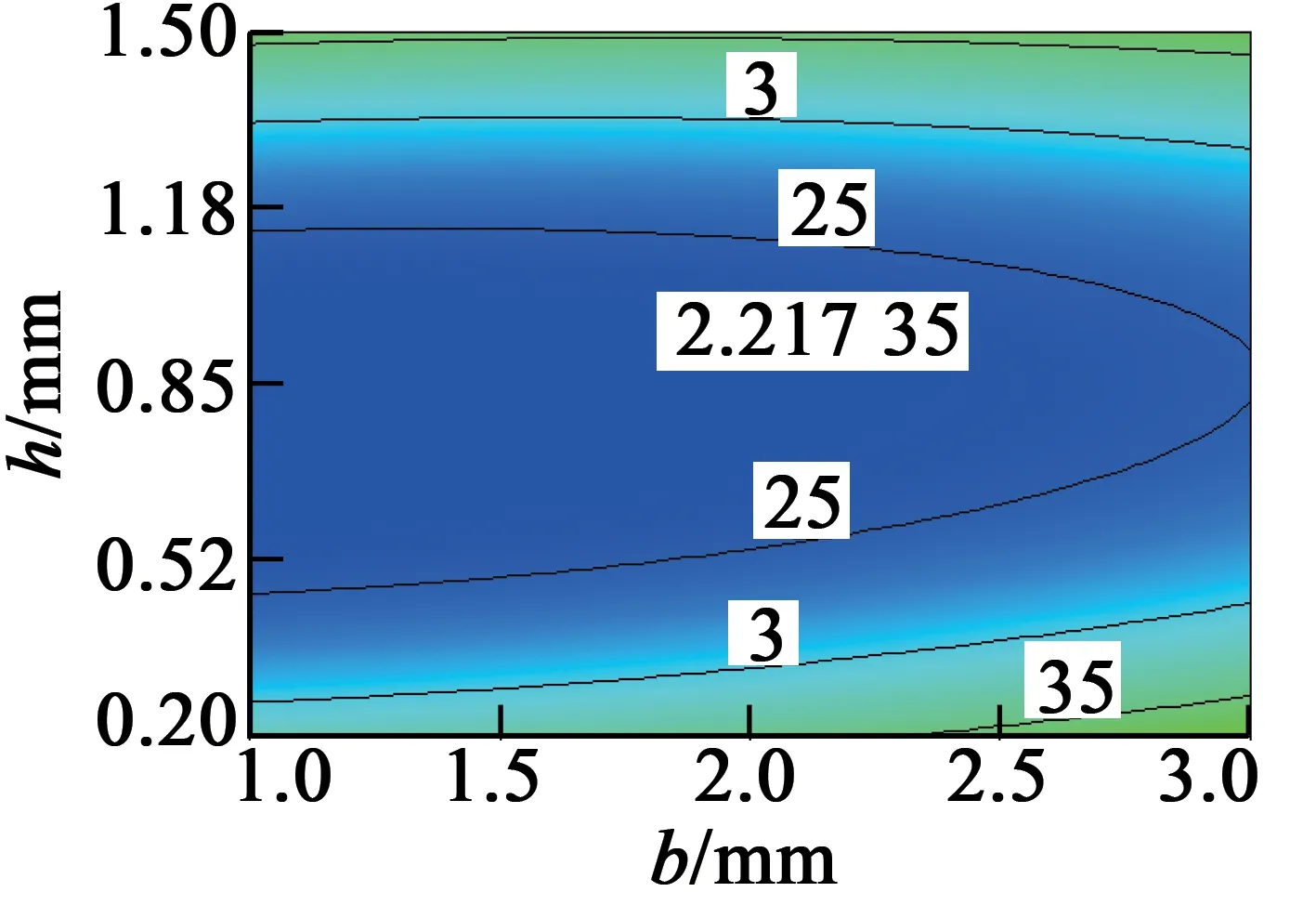
(a) 等高线图

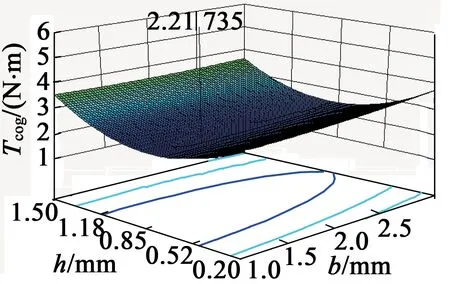
(b) 三维响应图

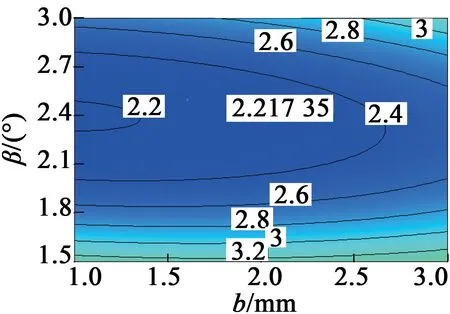
(a) 等高线图

(b) 三维响应图

(a) 等高线图

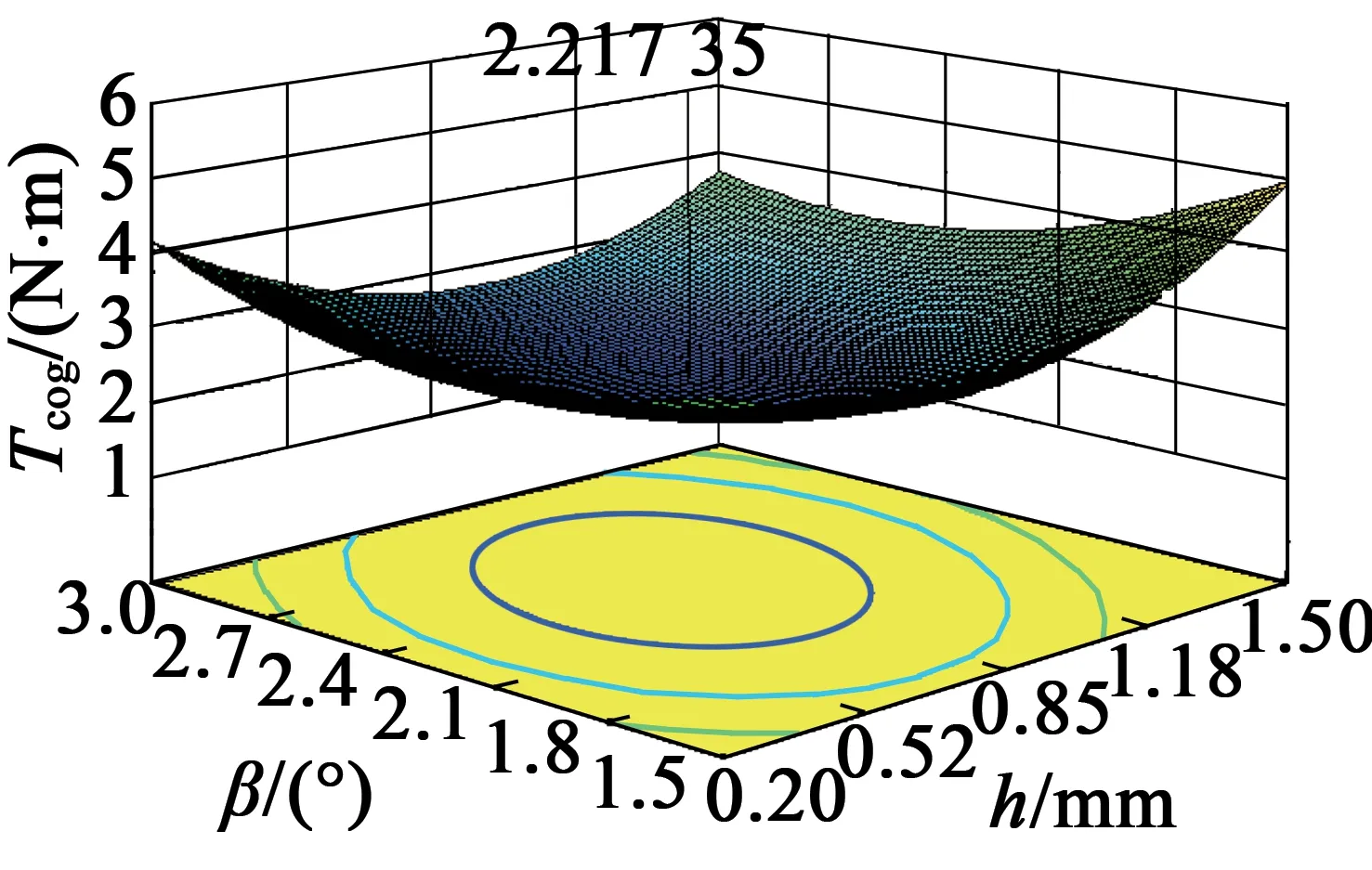
(b) 三维响应图

由图6～图8可知，辅助槽槽宽对齿槽转矩的变异影响较小，而槽深和槽中心线夹角对齿槽转矩的变异影响较为显著，验证了永磁轮毂电机回归模型的合理性，同时也反映了辅助凹槽尺寸合理性程度。

利用Design-Expert软件对二阶回归模型分析求解得响应曲面优化的最优辅助槽尺寸为(x1,x2,x3)=(1.58,0.87,2.35)，响应函数的齿槽转矩为y=2.217 35 N·m。

对响应曲面法求得最优解b=1.58 mm,h=0.87 mm,β=2.35°，进行有限元仿真如图9所示。

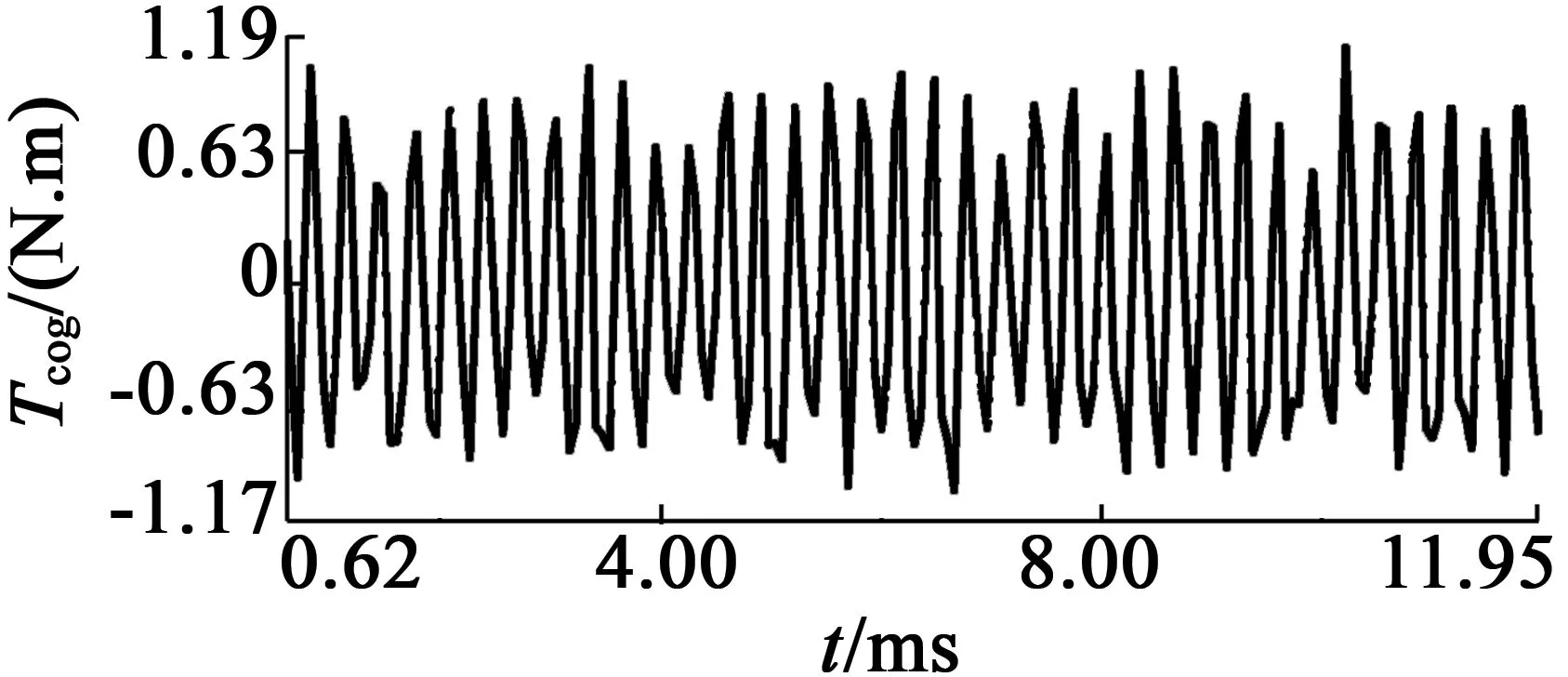
图9 齿槽转矩的仿真结果图

有限元仿真得到齿槽转矩随着不同辅助槽尺寸的变化曲线如图10所示。

由图10可知，辅助槽尺寸对齿槽转矩的变化趋势。齿槽转矩随着辅助槽宽的增大而呈抛物线形式变化，在辅助槽深为0.9 mm和槽中心夹角为2.5°时齿槽转矩最小。与响应曲面法求得结果类似，验证了该方法的正确性。

(a) 不同辅助槽宽时的齿槽转矩

(b) 不同辅助槽深时的齿槽转矩

(c) 不同辅助槽中心线夹角时的齿槽转矩

如图11所示，开2个辅助槽有效地减少了轮毂电机的齿槽转矩，且优化前后辅助槽的齿槽转矩峰峰值由4.009 1 N·m下降到2.159 4 N·m，齿槽转矩下降了46%。通过有限元仿真结果与响应曲面优化后的结果对比可知，永磁电机齿槽转矩的峰峰值大小基本一致，验证了该方法的有效性。

图11 辅助槽优化前后的齿槽转矩波形图

4 结 语

本文针对永磁无刷轮毂电机开辅助槽时，辅助槽尺寸选取的问题，提出了采用响应曲面法优化辅助槽尺寸的新方法，新方法简单有效，运算精度高，能同时保证多变量之间的运行关系，且适用性强。通过比较有限元仿真结果与响应曲面优化结果，齿槽转矩的峰峰值基本一致，有效地验证了响应曲面法优化永磁轮毂电机辅助槽尺寸的可靠性和优越性。且从齿槽转矩仿真结果图和优化前后的齿槽转矩波形图可知开两个辅助槽有效地减少了轮毂电机的齿槽转矩，且优化前后辅助槽的齿槽转矩峰峰值下降了46%。

[1] 张科.永磁电机齿槽转矩研究[D].焦作:河南理工大学,2011.

[2] 曹翼,李光耀.不同极槽配合永磁伺服电机的电磁性能分析和比较[J].电机与控制应用,2015,42(11):21-25.

[3] 王轶楠,唐冲,颜钢锋.定子齿冠开辅助凹槽抑制永磁电机齿槽转矩[J].微电机,2014(10):20-23.

[4] 夏加宽,于冰.定子开辅助槽抑制永磁电动机定位力矩[J].微特电机,2010(1):13-14.

[5] 古江海,黄文美,王超. 定子齿开槽对内置式永磁电机齿槽转矩的影响[J].电机与控制应用,2016,43(8):40-45.

[6] 张科,史祥翠.永磁无刷直流电机齿槽转矩削弱方法[J].煤矿机电,2009(6):37-39．

[7] 谭建成.永磁无刷直流电机技术[M].北京: 机械工业出版社,2011．

[8] 雷静希,肖文生.设计参数对直驱永磁同步电机运行平稳性的影响[J].磁性材料及器件,2013(1):32-35.

[9] 周俊杰，范承志，叶云岳.盘式永磁电机齿槽转矩的分析与抑制[J].机电工程,2009(2):79-82.

[10] 翼溥,王秀和,王道涵,等.转子静态偏心的表面式永磁电机齿槽转矩研究[J].中国电机工程学报.2004(9):188-191.

[11] 彭峰,谷爱昱,梁德志,等.压缩机用无刷直流电机的设计与研究[J].机械与电子，2015(11):43-46.

[12] 上官璇峰，王秋. 响应曲面法优化深槽面贴式永磁同步电机[J].微电机,2015,48(12):20-23.

[13] HWANG K Y,LIN H,RHYU S H,et al.A study on the novel coefficient modeling for a skewed permanent magnet and overhang structure for optimal design of brushless DC motor[J].IEEE Transactions on Magnetics,2012,48(5):1918-1923.

[14] Karim Abbaszadeh,MostafaJafari.Optimizing cogging torque reduction in slot opening shift method for BLDC motor by RSM[C]//Power Electronics,Drive Systems and Technologies Conference.IEEE,2011:62-66.