元明时代的筹算开平方新法<br/>——连接传统筹算开平方与珠算开平方的桥梁

元明时代的筹算开平方新法
——连接传统筹算开平方与珠算开平方的桥梁

2018-04-27邹大海

自然科学史研究 2018年1期

牛腾邹大海

(1.中国科学院自然科学史研究所，北京 100190；2.中国科学院大学，北京 100049)

现存文献中，开方法最早见于《九章算术》中用算筹进行演算的“开方术”，后经刘徽、祖冲之、贾宪、秦九韶等人的发展，到宋元时期已形成可较为简便地求任意一元高次方程数值解的一般方法。珠算盘产生以后，先是发展出了四则运算的各种珠算方法，后来又发展出珠算开方法。前人对珠算开方法的发展已有一些较为初步的研究，但还有很多关键问题有待深入探讨，筹算开方如何过渡到珠算开方就是其中一个重要问题。由于相关文献的描述往往不太明确，所以这个问题又与如何判断古人描述的开方是筹算开方还是珠算开方的问题交织在一起。华印椿《中国珠算史稿》[1](以下简称《史稿》)、李迪主编《中国数学史大系第6卷：西夏金元明》[2](以下简称《大系》)、韩祥临《〈算法统宗〉与珠算》[3]等对判断标准有总结，但存在一些缺点。这方面的问题非常复杂，本文只重点审视开平方法从筹算到珠算的过渡。我们发现有异于传统筹算开方布局的一类筹算开方法——本文称为筹算开平方新法*这里所说的新法，并非指运算程序上有多大的进步，而是指这种筹算开方法与以前的筹算开方法相比，其各项在布局上呈现出新的特点，这些特点又出现在后来成熟的珠算开方法中，对于珠算开方法的产生有很关键的作用。，出现在元明算书中，这对于研究这种过渡十分重要。因此，本文将以此为突破点，通过对新法和旧法进行对比分析，结合明代中后期其他相关材料，对筹算开平方到珠算开平方的发展进行较为深入的研究。

这种筹算开平方新法，早在元明之际算书中的就有两种类型，一种见于贾亨《算法全能集》(具体时间不详)和丁巨《丁巨算法》(1355年自序)。山崎与右卫门等《珠算算法的历史》[4]、郭书春主编《中国科学技术史·数学卷》[5](以下简称《数学卷》)等论著已有提及，但未具体分析其运算过程，后者有的说明有不妥之处。另一种类型见于《通原算法》(1372)，李俨[6]、华印椿([1]，397～398页)、孔国平和李迪([2]，318页)、郭世荣和郭书春([5]，575页)、劳汉生[7]等对它属于筹算开平方法还是珠算开平方法持有不同的看法，本文认为仍是筹算开平方法。为便于对比，我们先介绍传统布算的筹算开平方法。

1 传统的筹算开平方法

元末明初的算书中只有《丁巨算法》载有传统布算的筹算开平方法，布算上基本继承了传统开平方法的特点，但在表述上却与之前的算书如《透廉细草》稍有不同。下面以两书中的传统筹算开平方法为例对传统筹算开平方的特点做一介绍。

1.1 《透廉细草》中传统的筹算开平方法

约成书元代而早于《算法全能集》、《丁巨算法》和《通原算法》的《透廉细草》*《透廉细草》现存71题，其中54题1814年由鲍廷博从《永乐大典》部分卷帙中辑出并刻入《知不足斋丛书》的《透廉细草》残卷，17题见于现存《永乐大典》卷16343和卷16344中。另外，清莫友芝所录《诸家算法》中的13题与《知不足斋丛书》中的后13题相同。三种材料都源于《永乐大典》。见邹大海：《透廉细草提要》[8]。，内有开方问题，其中有开平方细草的仅存一题，见于《永乐大典》卷16344*滕艳辉错误地认为《透廉细草》未单独给出开方的具体过程[9]，这是因为他没有看到《永乐大典》中所录《透廉细草》的内容，不知其中有开平方法细草。，属于传统筹算开方，可与新法对比。该卷相同处下录有《丁巨算法》，提供一种不同的解法，后面第2节会予以重点介绍。

《透廉细草》原题为：

今有平方积五万五千六百九十六尺，问一面方多少？

答曰：二百三十六尺。法曰：平方开之。[10]

根据术文，下面分别用算筹和阿拉伯数字说明其运算过程(表1)。

表1 用算筹和阿拉伯数字展示《透廉细草》开平方过程

① 《十三、十四世纪中国民间数学》误作“三”( [6]，9 页) 。② 原文误作“十”，李俨亦从之( [6]，9 页) ，今据算理校正为“千”。③ 原文误作“百”，今从李俨校正为“十”( [6]，9 页) 。④ 原文误作“二”，今从李俨校正为“一”( [6]，9 页) 。⑤ 原文“六尺”下有“一步”二字，疑因古代六尺为一步而误衍“一步”，今删之。

1.2 《丁巨算法》中传统的筹算开平方法

丁巨收集了不少算书来研究算学，在《丁巨算法》*《丁巨算法》原8卷，现存仅90题，有两个来源。一为清《知不足斋丛书》中的《丁巨算法》残本，存62题，二为现存《永乐大典》卷16343、16344所录《丁巨算法》，存28题。另外，《诸家算法及序记》录有28题，与前者的后28题相同。([5]，526页)自序中称：“因于算术，上自《九章》，下至小法，数十百家，摘取要略，述《算法》八卷。”[11]开方法的记载不存于传本知不足斋本《丁巨算法》残卷，只见于《永乐大典》卷16344所录该书。其中除传统的开方法外，还有新的开方法。书中传统开平方法只有一例，前人未做具体讨论，却有助于我们进行对比研究。

《丁巨算法》原题为：

今有平方积六十二万二千五百二十一尺，问一面几何？

答曰：七百八十九尺。[10]

下面对照术文，分别用算筹和阿拉伯数字说明其运算过程(表2)。

表2 用算筹和阿拉伯数字展示《丁巨算法》传统筹算开平方法

续表2

① “倍方法八”是指把方法148 中的8 加倍，加倍以后要往高位进一，方法就变成了156，所以下文说“得方法一百五十六”。

1.3 《透廉细草》、《丁巨算法》中传统筹算开平方法的比较

结合两算书的筹算开平方细草，本文发现如下共同点：(1)布算分商、实、方、“借算”(本文用“借算”代表隅、隅法或约法等名称)四项从上至下排列；(2)借用一根算筹确定商的位数和方法的位置，且“借算”有进退位变化；(3)布算中用到“方法”，且有退位变化；(4)每次商数做乘减运算时，不论该商处于哪个位上都只视为一位数参与运算。

除这些共同点外，两算书还有以下不同之处：(1)对于商数的摆放：《透廉细草》各位商数的位置与被开方数的相同，即商数的第n位(按从低到高的顺序，下同)在被开方数的第n位上方；《丁巨算法》各位商数的位置与“借算”(隅法)相同，因而相对于被开方数各位的位置来说，商数的各位是隔位放置的，即商数的第n位放在被开方数的第(2n-1)位之上方。(2)在《透廉细草》中，新得的商先与“借算”(隅法)相乘，再加入上一步的旧“方法”，形成新的“方法”；而在《丁巨算法》中，新得的商产生的那部分“方法”在位置上不是直接而是间接通过由“借算”(隅法)确定的商的位置来确定加入到哪一位的，并且这部分“方法”在乘减之前是直接放入旧“方法”之中的，这里用数字的直接放置代替了加法运算，如“上商八，呼一八生方八。于方法之后，对上商八之下布方法八”。(3)对每一步放置数字，《透廉细草》表述为“上商二百尺”、“得二万为方法”，都明确说明具体的数值；而《丁巨算法》由于采用上述第(2)项中的定位方式，在描述“商数”、“方法”时只直接写出所在位上的数字，如“上商七”、“布七作方法”中的“七”分别表示“七百”和“七万”。(4)在对运算过程的描述上，《丁巨算法》更详细，如对其中涉及的乘法运算都用相应的九九口诀进行了说明，如“呼四八三十二，去积三万二千尺，又呼八八六十四，去积六千四百尺”等；《透廉细草》只有“命商除实”一句，而不具体描述运算的过程。

综上，以上两书中开平方的传统方法基本上延续了《九章算术》以来的开平方法的布算特点，但对过程的叙述较为详细，《丁巨算法》尤其如此，这也是当时大部分算书中的细草所共有的特点，体现了当时数学文献注重实用化和大众化的倾向。值得注意的是，以上两算书中传统筹算开平方法在布算上所具有的某些特征，在元末明初的开平方新法中已不见踪迹，下面予以具体介绍。

2 元末明初开平方新法分析

除传统布算的筹算开平方法之外，《丁巨算法》还记载了一种新的开平方法，布算上与之前有很大不同，《算法全能集》也记载了这种新的开平方法。《通原算法》则记载了不同于传统布算而又异于上述开平方新法的另一种开平方法。下面对这两种开平方新法进行具体的分析和新的阐释，并澄清以往研究中存在的一些问题。

2.1 《算法全能集》和《丁巨算法》中的开平方新法

华印椿先生在提到元代《算法全能集》、《丁巨算法》等算书记录的开方法时，说它们都有以下特点：借一算为下法，以定商位；在运算过程中，下法和廉法须分别退位。华先生以此断定它们都是筹算开方[1]，但他没有注意到两书都记载了没有以上特征的新的开平方法。山崎与右卫门等[4]虽提到《算法全能集》的开平方法与以前的方法有不同之处，但对不同之处没有具体说明。《数学卷》称这种开平方法为一种“试商后直接减积”的开平方法[5]，但解说有些不妥之处。本文将对这种开平方新法的布算及运算进行具体分析和详细解释，表明这种新的开平方法确实可判断为筹算开平方法，但本文的判别标准与华先生不同。另外，开方法与商除法关系密切，本文也通过对商除法的分析以辅助说明有关问题。

《丁巨算法》原题与《透廉细草》题目相同(见第1节，此处略)，但解法不同。下面对照术文分别用算筹和阿拉伯数字两种方式展示整个运算过程(表3)。

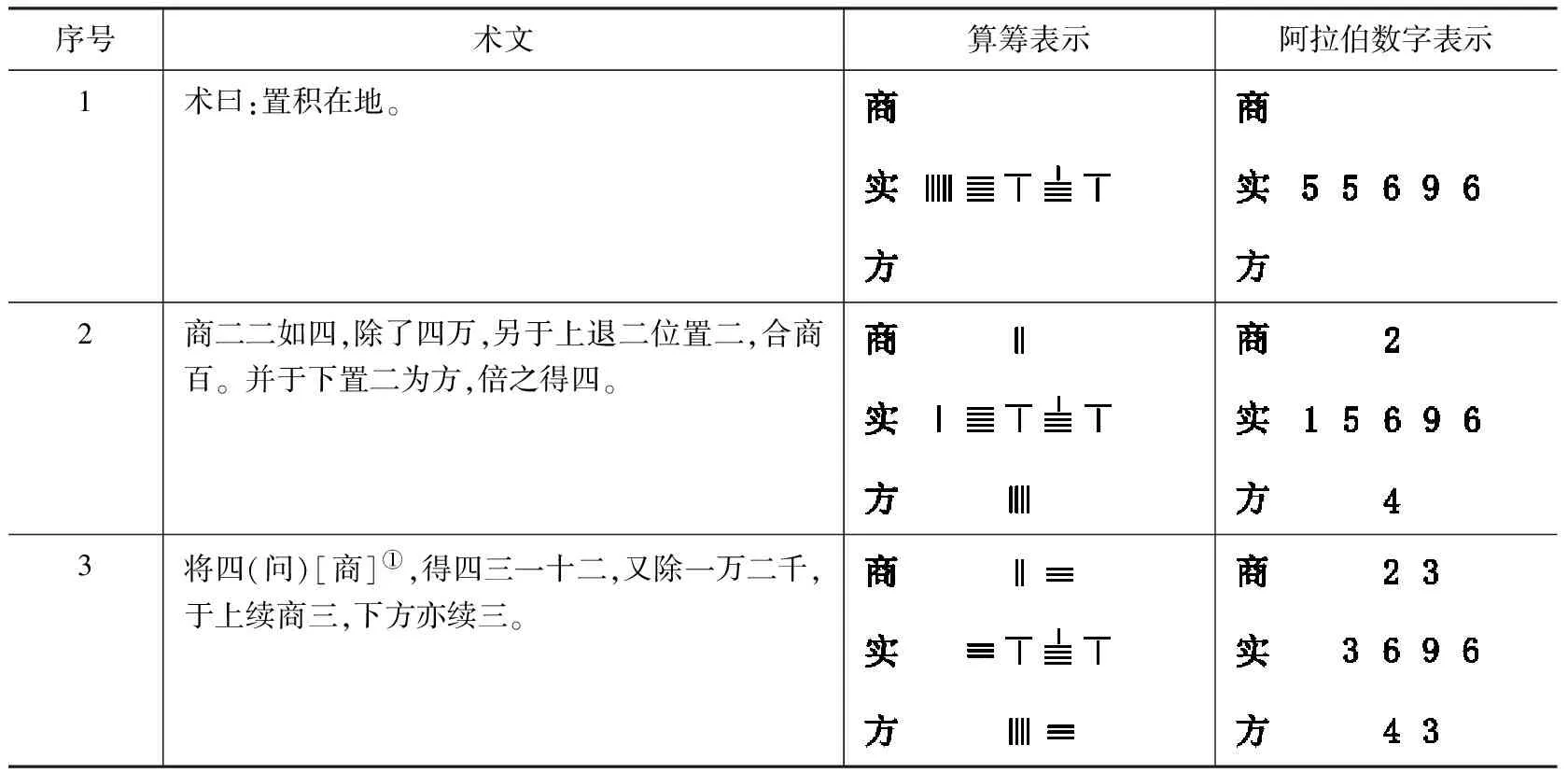
表3 用算筹和阿拉伯数字展示《丁巨算法》筹算开平方新法运算过程

① 原文作“问”，今校改为“商”。可能“商”字上半部残损，之后又被误识为“问”。

续表3

① 可能因为第三位商使乘减后没有余数，作者用了一个简省的表述，没再给出细节。据前面的行文习惯，可将步骤补全为: “下方亦续六，又将上下六为六六三十六，又除三百六十。又将上下六为六六三十六，又除三十六。适尽。”

通过上述布算发现，此开平方法布算分商、实、方三项从上至下排列；没有“借算”；“方法”没有退位变化*“方法”由商的位置确定后，不再需要也不能进行退位变化了。；每次商数做乘减运算时，都是其本身的数值参与运算。事实上，《丁巨算法》的这种新算法与传统开平方法相比，只是更侧重于对新产生的商数和方法之位置做出说明，两者位置相同，后者由前者决定，如“于上续商三，下方亦续三”。又术文中有“置积在地”、“另于上退二位置二，合商百”等描述，可知是用算筹布算。

贾亨《算法全能集》所载开平方法与《丁巨算法》中的新方法相同，但比《丁巨算法》多了开平方歌诀，这也是目前所见最早记载开平方歌诀的算书，其原文如下：

二十开平方謌曰

开方以积使商除，除得其间上置诸。

下另倍为方法数，却将方倍减其余。

得其次数上商续，方下傍边也续欤。

上下再将续除积，积之数尽自昭如。

若还不尽倍方次，逐一将方位数除。

除见数来商又续，只将此续取空虚。

开方之法有三：有平方，有直方，有立方，其法最难收算，然公私亦少用之。但平方一法，间有用之收算方田一面，不可不载一法于其间也。[12]*此说明文字后所载例题与上述《丁巨算法》中“今有平方积五万五千六百九十六尺”例题相同，且例解基本一致，如最后“续商六”之后直接是“以六除，尽”，没有详述如何“以六除”的过程。说明《算法全能集》和《丁巨算法》有很大渊源关系。

通过对歌诀和其下例题开方解法的运算过程进行比对，可知两者相符。这说明编写歌诀的作者熟悉此开方法。另外，该书第17项“丈量田亩”中也有一开平方例题([12]，1339～1340页)，解法相同，即使此题的作者与歌诀的作者不是同一个人，也说明此题的作者是了解上述开方法的。

其实，《算法全能集》和《丁巨算法》开平方法“先减积再立商”的特点，在当时的商除法中就有所体现。《丁巨算法》中有这样一题：

今有面一百七十二斤零二两，卖钞二十五两五钱。问每两该面若干？

答曰：六斤一十二两。

其术文详载了商除法的运算过程：

此归除法也。置都斤在地为实，并二两为一二五在地。以二呼除二六一十二，另置商六。却于实上二位除五六三十、五六三十。其余数又呼除二七一十四，续商七。却于实上二位除五七三十五、五七三十五。再不尽，又呼除二五一十，续商五。却于实上二位又除五五二十五、五五二十五，适尽。又以七五为一十二两。合问。([11]，1312页)

术文中“归除法”，据其下所载运算过程，实为商除法。因为书中第13题的解法中提到“归除”，正是归除法，与本题所谓“归除法”迥异，故原文“归”很可能是“商”之误。另一种可能性是，这里的“归除”只是指明是除法，不一定是指具体计算上与商除相对的归除。无论如何，这里的除法本身肯定是与归除法相对的商除法。

术文中“呼除某数”再“另置商某数”或“续商某数”的表达方式正好体现了商除法与上述开平方法中“先减积再立商”的特点。如果上引例子还因为术文“归除”二字有疑问的话，那么下引《算法全能集》关于商除法的歌诀和例题就很清楚了：

商除謌曰

法使商除把总张，却将分数作商量。

可除一面除将去，除尽其间数便当。

商除者，商量而除之也。凡遇均分钱物，以合分分数为法，除见合得之数，另置于上*此处“除见合得之数，另置于上”与该算书开平方歌诀“除得其间上置诸”刚好对应。，以在地数尽为度。不尽，又从而续商，故谓之商除。……

今有军六百名，分粮三百九十四石二斗，问每人该粮几何？

答曰：每人该粮六斗五升七合。

法曰：置都粮在地，以六呼除六六三十六，另置商六。余数又呼除六五三十，续商五。不尽。又呼除六七四十二，续商七。恰尽。是数合问。([12]，1324页)

其中“商除”的称谓和具体的计算方式与上引《丁巨算法》“此归除法也”下的计算方式的一致性正好证明了上述结论。

再如元末安止斋、何平子《详明算法》(1373年刊本)有关于商除法的歌诀和解释：

商除

数中有数号商除，商揔*“揔”，同“总”。下同。分排两位居。

唯有开方须用此，续商不尽命其余。

……

商除者，商量而除之也，此一术亦兼九归、定身除、归除三法。既通归除，不必学此。但开方则必须商除，故不可废其法。置揔数商量除讫，却将所商之数，别置一位下之，逐位续商尽而止*“逐位续商尽而止”，可能是“逐位续商，商尽而止”之误，可能流传过程中“商”字下脱重文号“=”。。有不可尽者，则之命。[13]②*朱希安等认为《算法全能集》和《详明算法》中的商除法是将古法上商、中实、下法的三行式改排为左商、中实、右法的一行式，并称这是将筹算方法直接搬上算盘的表现[14]。此说法不妥。首先从《详明算法》的歌诀及对应的解释可知，其布算只有“商”、“总数”两项，未见有“法数”的布算说明；其次，商数“另置于上”中的“上”字解释为左边比解释为上方需要更多的证据；商数“别置一位下之”是另外安排一个位置放下算筹来表示商数的意思，其中“下”字不是指下面，而是动词，表示放下(算筹)之义，应该是指放在上方。即使在左边，同样可以是使用算筹，不一定是用算盘。况且如果是用算盘，则商数在左边，不能用“下”，只能说“上”字(如果不用“左”字的话)来描述。另外，“则之命”疑当作“则以法命之”。

从以上歌诀和例解可看出，元末这三部算书所记载的商除法，都是在运算时先心算得商数，但不立即放置，而是先用商数与法数相乘，从实数中减去所得积以后再放置商数。这与《算法全能集》和《丁巨算法》开平方新法中这一步的运算特点一致，可见商除法与这种开平方新法关系紧密。这也说明，《算法全能集》相关算题的作者确实了解这种新的开平方法。

《数学卷》称：

此方法中初商和次商都是直接将试商的平方从实数中减去，而且次商是用方法与余实商除而得，朱载堉与程大位等人的归除开平方法与此极为相似。[5]

本文的看法有所不同。首先，朱载堉与程大位的归除开平方法中初商均由口诀求出，实际操作时前者先立“下法”(《算法全能集》和《丁巨算法》称之为“方法”)，然后用归除口诀，在得到商数的几乎同时，从实数中减去了商数的平方，这也是归除法的特点；程氏先在实数的左边和右边分别放置初商与等于初商的数(称为“方法”)，然后从实数中减去初商和方法的乘积。其次，朱、程归除开平方法求次商亦均采用归除法，这也是归除开平方法与商除开平方法最大的不同。

总之，《算法全能集》、《丁巨算法》中开平方新法的产生与当时商除法的改革密切相关。与传统筹算开平方相比，新法简化了不少步骤，如布算上不仅少置“借算”一项，而且也不需要将方法退位、移动算筹，这既节省了步骤也减少出错的机会*方法退一位时，数值缩小到1/10，严格地说需要把算筹的纵式变成横式、横式变成纵式，这会增加出错的机率；但不做改变也对计算没什么影响，没有材料说明古人是否严格地做这种改变。。《通原算法》载有与之相似的另一种筹算开平方新法，但两者在布算和运算过程上还是有很多不同之处。

2.2 《通原算法》中的开平方新法

严恭《通原算法》2卷，原书不传，现存仅64题，其中29题存于《诸家算法》，35题存于《永乐大典》。([6]，25～43页)洪武壬子年(1372)潮州府赵瑀序说，严氏自称在元朝时曾收集一些数学书，因元末兵乱而散失；他在明初“默集”而编写是书，以补算书之缺失。([10]，1455页；[5]，531页)那么，《通原算法》所载开平方法或许在元末之前就已存在。有细草的开平方题目现存两题，见于《永乐大典》卷16344。

前人对《通原算法》中开方所用工具是算筹还是算盘有不同意见。李俨曾对书中的开平方法用筹算加以解说，其算筹图式中有“下隅”的退位变化[6]，其实并无退位。华印椿说此书开平方不用借筹定位，运算时也不做退位处理，书中找不到筹算的证据，进而否定李俨关于是筹算开方的判定，而改判为珠算开平方法。([1]，397～398页)劳汉生与华氏的看法相同，依据也相同。[7]孔国平在李迪主编的《大系》中提到，《通原算法》中载有筹算开平方、开立方法。([2]，318页)《数学卷》介绍了《通原算法》的开立方法，也认为它属于筹算开方。([5]，574～575页)下面我们首先对《通原算法》开平方细草进行具体分析，而后对所用算具做出新的判断。

《通原算法》开平方术文中有“借一筭，步之超一等”，虽然“借算”(原书下文中称为“下隅”)在后面的运算中没有退位变化，但一直参与运算，如“上商二百乘下隅为廉二百”、“续上商六十，乘下隅为廉六十于四百之下”，可见运算过程中确实借一算筹作为“下隅”项而占用一行布算，并有进位变化。这可说明其开方法用算筹布算的可能性最大。

《通原算法》原题为：

今有积七万一千八百二十四步，问为方几何？

答曰：二百六十八步。([10]，1417页)

下面依照原文分别用算筹和阿拉伯数字两种方式展示整个运算过程(表4)。

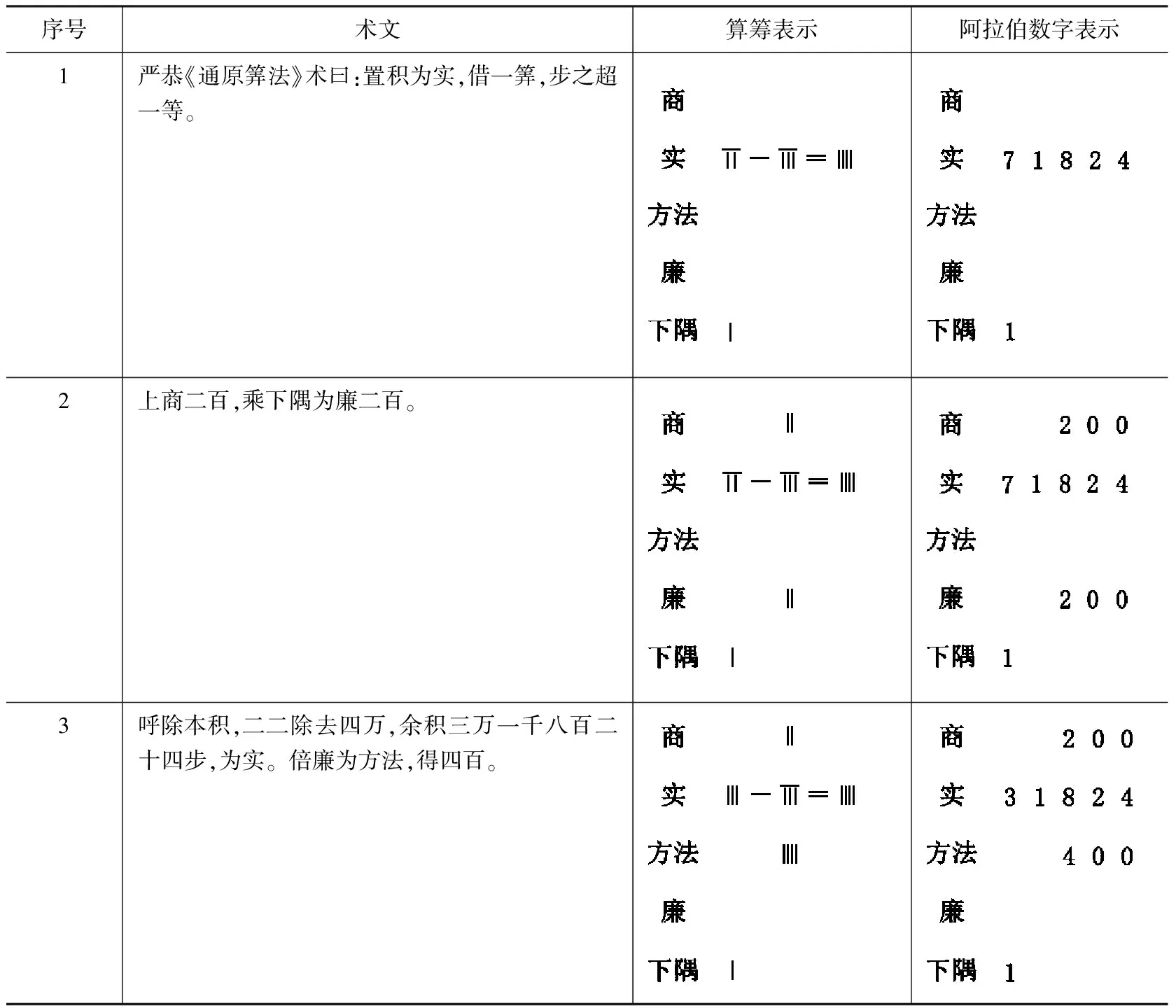
表4 用算筹和阿拉伯数字展示《通原算法》开平方过程

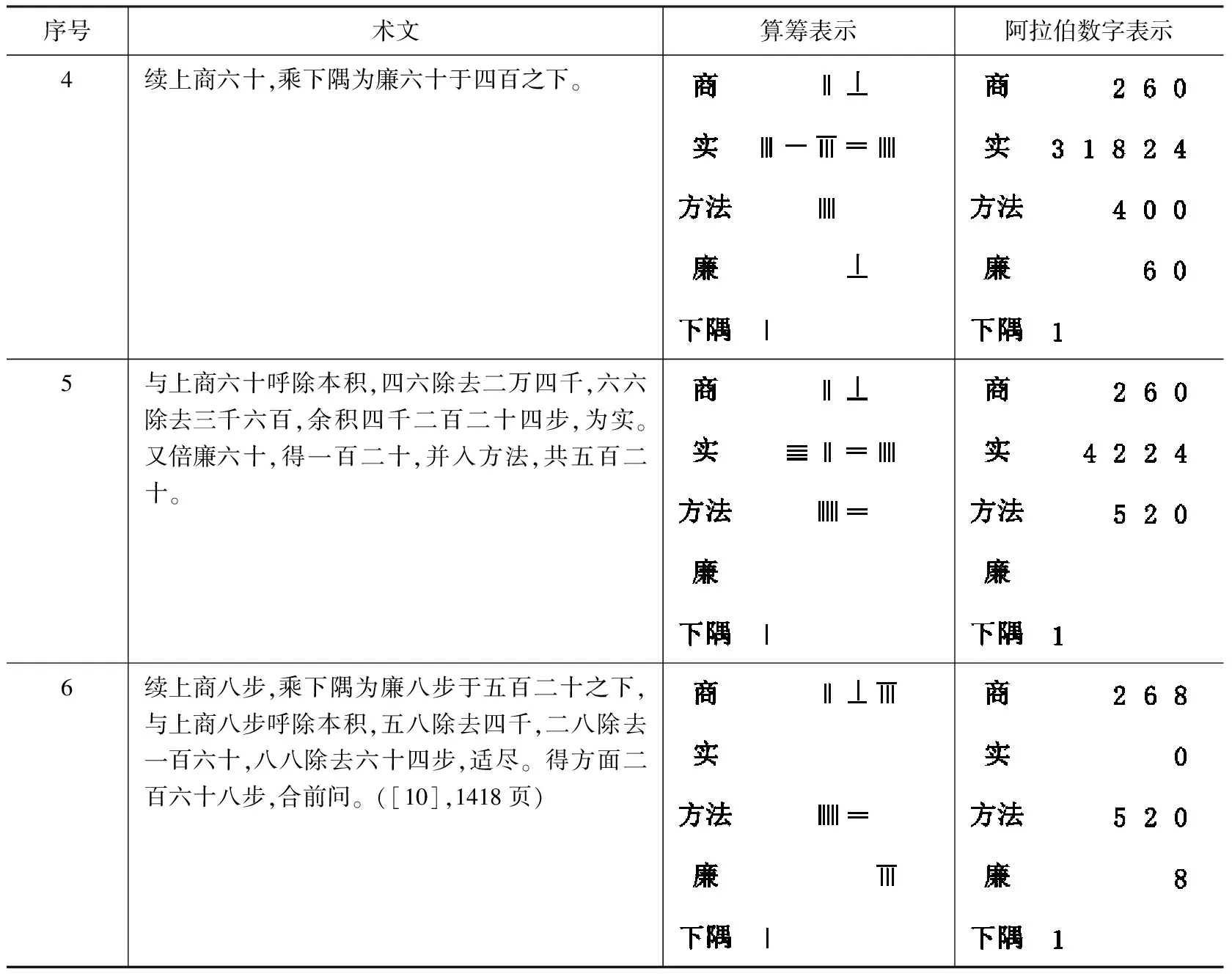
续表4

严敦杰认为此书可能用到珠算，否则不会用“呼”、“再呼”等词。[15]其实，《算法全能集》、《丁巨算法》等书中的开平方法也用“呼”字。九九歌诀至迟在战国时代就已存在，元明之际算法歌诀化盛行，又属于算筹和算盘并存的时代，使用算筹时说“呼”字也很正常，单凭“呼”字至少不能判断上述开方为珠算开方。由于有商、实、方法、廉、借算(下隅)五项，又用“上”、“下”指明置数位置，因此这里开平方所用工具当属算筹无疑。

根据表4所示，《通原算法》中的开平方法，与传统布算的筹算开平方法相比有以下不同点：(1)有“借算”，但无“借算”的退位变化。这点上我们与李俨的看法不同，因为原文除“借一筭，步之超一等”以外，并未提到“下隅”的其他位置变化，若依照传统开平方算法加上“下隅”的退位变化，则没有任何意义，反而使运算步骤更加繁琐。(2)整个开平方过程中没有方法及廉的退位变化，在进行下一步置商之前，廉位上的数字在加倍并入方法的时候，就清空了。

本文还发现，《通原算法》开平方法中的“借算”仅起到确定商数的位数的作用，并没有确定商数、方法、廉法之位置的作用。虽然运算过程中没有了复杂的退位变化，但严恭开平方法布算用到5层，未免繁琐。另外，传统布算的筹算开平方法中，方法乘商以减积或余积时，商数往往不带位值而乘[16]，而《算法全能集》、《丁巨算法》以及《通原算法》所载开平方新法中的商数在参与运算时明显是带有位值涵义的。

3 筹算开平方新法与传统筹算开平方法的特点分析

上面对元末明初《算法全能集》、《丁巨算法》、《通原算法》三部算书开平方法的分析，说明它们在叙述上有各自的特点，其中开平方新法与传统的筹算开平方法相比，在布算上出现了很大的变革。下面将以《透廉细草》为代表的传统筹算开平方法与上述三部算书中的筹算开平方法进行布算上的对比(表5)，以便对筹算开平方法的特点进行新的分析。

表5 四种算书(现存内容)中开平方法的布算特点分析

① 原文中称为“约法”、“常隅”、“下法”或“隅法”。② 原文中称为“隅”或“隅法”。 ③ 原文中称为“下隅”。

根据表5，筹算开平方法在布算上有以下共同点：皆为纵式排列；必有商、实、方三层，多者达五层。另外，这些开方问题都属于商除开方法，与商除法的发展密切相关，而与归除法没有关系。这一时期既有传统筹算开平方法，又出现了至少2种筹算开平方的新法。新法的共同特点是没有方法(廉、隅)的退位变化。《算法全能集》和《丁巨算法》中的开平方新法，只有商、实、方三项分三层布算(以下简称此法为“三层新法”)，《通原算法》的开平方新法在开始时有借算的进位变化，但完成确定商数之位数的功能后，转化成了下隅，也没有退位变化了。《通原算法》的开平方新法布算用到五层(以下简称此法为“五层新法”)，多了廉、下隅二项，且从商第二位数起都要置廉，这仍显繁琐。所以五层新法较之三层新法要原始一些。从算理上讲，传统筹算开方可能先发展到五层新法，然后改进到三层新法(赵序《通原算法》的年份不见得是五层新法的初创时代)，它们都处于改革筹算开方的阶段。

下面将上述筹算开方新法与后来出现的珠算商除开方法进行比较，可以发现两者有很多相似之处，这为我们认识珠算开平方法的产生与发展提供了新的视角。

4 筹算开平方新法与珠算商除开平方法的比较

4.1 从《算法统宗》看筹算开平方新法与珠算开平方

珠算开平方分为商除开平方和归除开平方，前者明显是继承筹算开平方法而来，而在文献中我们也没有发现与珠算归除开方法对应的筹算归除开方法。所以，这里我们重点介绍珠算商除开平方法，分析其特点，以说明它与筹算开平方法的不同类型之异同。

现有材料中，明代王文素《算学宝鉴》(1524)已出现看似是珠算开方的商除开平方法，但没有明确说明运算工具。我们通过分析书中描述开方过程的文字和图式，可知属于筹算开方(我们另文做专门讨论)。明确属于珠算商除开平方的材料见于余楷《一鸿算法》(1585年刊印完成)、程大位《算法统宗》等书中。因《算法统宗》所著珠算商除开平方法较为详细、全面，且有与上述筹算开平方新法相类似的方法，而开平方例解中又明确所用计算工具为算盘，还详载运算图式，所以本文以此书为例介绍珠算商除开平方法及其特点，在此基础上讨论珠算商除开平方法与筹算开平方新法之间的关系。

程大位在编写《算法统宗》时“参会诸家之法”，直接参考过的著作有40种左右([5]，560页)，包括吴敬《九章算法比类大全》(1450)和余楷《一鸿算法》[17]，其中开平方的很多内容也有参考过前人著作的痕迹。该书载有“开平方法认商歌”：

开平方法认商歌

一百一十定无疑，一千三十有零余。

九千九九不离十，一万才为一百推。

得商方除倍作廉，次商名隅并廉除。

余数续商隅又倍，只依此法取空虚。([17]，1308页)

前四句是对求初商数值的一般说明，与《九章比类》“开平方法”歌诀[18]和《一鸿算法》“开平方认商歌”[19]中的前四句都基本相同；后四句是对商除开平方法运算过程的说明。其中“一百一十定无疑”、“一万才为一百推”相当于开平方法中的“言百之面十，言万之面百”。

随后又有“开平方初商定首位诀”

开平方初商定首位诀，是自乘之数也。

商一步，积一步；商一十步，积一百步；

商二步，积四步；商二十步，积四百步；

……

商九步，积八十一步；商九十步，积八千一百步。([17]，1308页)

接下来给出具体的开平方法(为便于下文分析，记为“诀”下开方法)：

法曰：置积为实。别置一筭，名曰下法，于实数之下。自末位至首，常超一位。约实。一下定一，(千)*原文“百”字前有“千”，郭世荣亦从之[20]。据算理，此“千”字为衍文，今删之。百下定十，万下定百，百万下定千。实上商置第一位得若干，下位亦置上商若干，名曰方法。与上商相呼，除实若干，余实若干。乃以二乘方法即倍法也，得若干为廉法。续商置第二位于上商之次，得若干，下法亦置续商若干，为隅法，于倍方之次，共若干，皆与续商相呼除实，尽，得平方一面数。如不尽，仍前再商之。([17]，1308页)

上引开平方“法曰”下的文字，在表述上与筹算开方法基本相同，如“实数之下”、“实上”、“下位”、“上商”等词的使用，以及对“借算”的说明：“别置一筭，名曰下法，于实数之下”。郭世荣认为此处讲述珠算开方术，“别置一筭”系借用筹算开方术语，这“一筭”其实是虚置，在算盘上并不显示([20]，243页)。如果按《算法统宗》卷1“用字凡例”中所说“上脊梁之上，又位之左”，“下脊梁之下，又位之右”([17]，1230页)，那么这一理解也是有道理的。但是，“上”、“下”毕竟可以不针对算盘而言，按通常的意义分别表示上方、下方。比如，同页说“大圈之下小圈，乃暗子马数”，就是讲右边一竖列符号中，含有大圈的符号下面的小圈内的符号是暗子马数。所以，尝试不按珠算开方来理解上面的方法也是完全可以。

我们发现，如果按筹算来理解反而更合适。首先，如上面已经谈到的，其文字本身是算筹开方的表述。其次，在上引“法曰”文字之后不远处，有“方廉隅法之图”，用以说明用分割正方形来展示开平方的道理。其下有一个开平方的问题(记为“图”下开方法)作：

平方积三百二十四

法曰：置积三百二十四步为实。○约初商一十步于实左，下法亦置一十步于实右，名曰方法，与上商相呼，一一除实一百步，余实二百二十四步。就以方法一十步，倍之得二十步，名曰廉法。○又约次商八步于左初商一十之次，共得一十八步。亦置八步于实右廉法二十步之次，名曰隅法，共得二十八步，与左位次商八步相呼，二八除实一百六十步。又左八对右八相呼，八八除实六十四，恰尽。得方面一十八步。([17]，1309页)

这里只用“左”、“右”，完全不用“上”、“下”来表示方位(不考虑作为专门术语的“下法”)，对比“诀”下开方法的文字中只用“上”、“下”，可谓泾渭分明。因此可以推论，与“图”下开方法不同，“诀”下开方法描述的是筹算开平方法：(1)分商、实、方法、廉法、下法(隅法)五层(亦可能是四层，在计算过程中方法改称廉法)；(2)方法、廉法、下法没有退位变化，下法只在开始有进位变化，用以确定首商在哪一位。对比前面所论筹算开方新法，可以看出，这里的开方法与之同类，且更接近五层新法。

“图”下开方法从左至右排列三项，中间为实(被开方数)，左边为商，右边为法：初名下法，后名方法、廉法，三个名称只是一项，最后的隅法与廉法合成一项(亦可能是在廉法与新加入的数合成后改名隅法)。这是珠算开平方法，其左中右三项与筹算三层新法的上中下三层相对应，但前者中实右边的那项有下法、方法、廉法等名称的变换，而后者中实下面的那项始终只有方这一个名称。从用语上看，这种珠算开平方法与筹算五层开平方法有更接近的地方，但前者的同一项有多个名称，而后者本来就是几项以不同的名称分置于不同的层。所以从本质上讲，这种珠算开平方法与前面所说的三层新法更接近。

元末明初的开平方新法和上述《算法统宗》“诀”下开方法，都是对传统筹算开方进行改革的例证，“图”下开方法虽为珠算开平方法，也反映了这种改革的踪迹。这些例证在布算层数、用语、计算顺序、是否进退位上互有异同，而没有两个是完全相同的，展示了这种改革的多样性。但无论如何，它们都有一个共同点：没有退位的变化。正是这一特点，为筹算开方过渡到珠算开方清除了很大的障碍。

上述“图”下开方法虽为珠算开方法，但在表述上还遗留着筹算开方法的一些痕迹，而下面围棋问题中的珠算开平方法，其陈述则很成熟了。这个问题是：

假如今有围棋盘，共子三百六十一个，问每面子若干？答曰：每面一十九个。([17]，1309～1310页)

其解法分两部分，第一部分为紧接在答案后的文字描述，我们用算盘图示直观解释原文(如表6)。

表6 用算盘展示《算法统宗》开平方过程

解法的第二部分是，用文字性的计算图式列出“开平方法定分左中右式”(图1)。这部分有廉法、隅法，而第一部分原文没有，在表6算盘图示中我们标出的“廉法”、“廉”、“隅”是据第二部分添入的。对于用算盘进行具体计算来说，添入这些文字并非必须。第二部分用方法、廉法和隅法进行说明，从计算本身来说也是不必要的，正如前面的三层新法一样。但程氏仍用这样术语，能更好地呼应前面的“方廉隅法之图”以展示开平方法的道理。

图1 《算法统宗》围棋题([17]，1309～1310页)

可以看出，相比于传统的筹算开平方法，《算法统宗》的珠算开平方法有以下几个特点：(1)没有“借算”；(2)没有方法及廉隅的退位变化；(3)只列商数、实数、下法三项数据；(4)三项数据在算盘上按从左至右的顺序排列；(5)在叙述上对运算过程的描述比较详细，如对其中涉及的乘法运算都用相应的九九口诀进行了说明。这5个特点中，第1点正是《算法统宗》珠算开平方法与上述筹算开平方的三层新法之共同点，第2点则是它与上述各种筹算开平方新法的共同点，第5点也与筹算开平方新法相似，第3点与三层新法的特征相同。可以说，如果不考虑算具之别，上述珠算开方法和筹算开方新法的区别关键在于数据的排列是左右横向排列还是上下纵向排列。

《算法统宗》的珠算开平方法与传统筹算开平方法差距很大却非常接近筹算开平方新法，这反映出其珠算开平方法由筹算开平方新法直接改造而来，而非直接改自传统筹算开平方法。前人对此没有清晰的认识，故而常常忽略筹算开平方新法，仅对珠算开平方法与传统筹算开平方法进行分析，因而得出了一些片面的结论。下面对此再做分析。

4.2 判断筹算开平方与珠算商除开平方法的标准问题

对筹算开平方法与珠算开平方法的不同点，华印椿《史稿》[1]、韩祥临《〈算法统宗〉与珠算》[3]和李迪主编《大系》(这部分亦由韩祥临执笔)[2]做过分析和总结。华先生还称，按照他对两种开方法特点的分析，可以鉴定元、明算书中记录的开方属于筹算还是珠算。由于没有注意到元末明初以来著作中的筹算开平方新法，他们对筹算开平方法特点的分析比较片面，以致其判断筹算开方和珠算开方的标准也比较片面、不太客观。现将三种文献所总结出的筹算开平方法和珠算开平方法之不同点与实际不符之处列出，如表7：

表7 华、韩、李论著所列筹算开平方与珠算开平方法的不同点与不符之处

① 华判为珠算开方的《通原算法》开平方法有5 项，与他所列珠算用3 项的标准相矛盾。

续表7

可见，这些著作对筹算开平方法特点的总结并不全面而准确，其标准无法对各算书中开平方法所用工具究竟是算筹还是珠算盘做出正确的判断。需要说明的是，一般所说的筹算开平方法和珠算开平方法很大程度上指的是开方的主体布算(布置各项)所用算具为算筹还是珠算盘，前者并不排除开方运算的主体上用算筹布算而某些中间环节用珠算的可能，毕竟最迟宋代已出现和现在形制一样的算盘，大量算法歌诀的出现，也使得珠算加减乘除法运算速度比筹算更快。所以，对于筹算开平方法和珠算开平方法的判定标准需要更细致的分类和更全面的分析。

目前看来，筹算开平方法与珠算开平方法在布算上最大的不同就是，前者的布算是各项用算筹从上至下排列，而后者则在一横行内从左至右排列各项*日本吉田光由《尘劫记》(1627)中有将筹算开方法各项数字直接用多个算盘来表示而形成的珠算开方法[21]，是筹算开方过渡到珠算开方的一种最直接且最简单的原始过渡形式。这种形式在中国也可能产生过，但现存中算著作中的珠算开方法都是各项在算盘上从左至右进行排列，而我们关注的是不那么容易判断的开方文献，所以本文所说珠算开方暂不包括这种情形。。在表达上，如果古人明确指出是用筹算开方或珠算开方，或明确表达出布算是上下排列还是左右排列，则可以很容易判断是筹算开方还是珠算开方法。如果没有这样明显的文字说明，但在描述运算过程时，有很明确的上下位置说明，或清楚地描述了某些项的进位或退位变化，特别是有下法(方、廉、隅)的退位变化，那么至少也可以确定总体布局上是筹算开方；而如果没有这种说明，那么是珠算开平方的可能性就很大了。但对于总体上是筹算开方的情形，亦存在珠算参与某些步骤的可能性：(1)如果被开方数的位数不多，数字不大，此时各步的计算简单，没有必要更换计算工具，因此珠算参与的可能性极小；(2)如果数据很大，各步的计算很麻烦，特别到16世纪或以后，则可能有珠算参与。

5 筹算开平方到珠算开平方法的过渡

有档穿珠的算盘最迟在宋代已经产生，像加、减这类简单的运算可直接移植到算盘上操作，乘、除这类复杂一些的运算在经过了算法改革后，也容易在算盘上实现。开方属于复杂的运算，以传统的筹算开平方法为例，最少用4层布算，其中实以下的各项在运算过程中还有进退位变化，若用算盘实现更是困难。因此，筹算开方(特别是传统的筹算开方法)过渡到珠算开方的过程不能简单地从算筹的几层纵式排列直接过渡到算盘上多项一行的横式排列。而较之传统筹算方法，把元末以来的筹算开平方新法移植到算盘上用一行横式进行操作，则要容易得多。

《算法全能集》、《丁巨算法》中的开平方新法布算只有3项，去掉了传统布算中的“借算”一项，省略了方法的退位变化等过程，在布算上比较简洁，这与后来的珠算开平方法非常相似。用算盘模拟其运算过程时，只要忽略其中对各项上下位置的说明，将它们从左至右在算盘上排列即可。但该方法在叙述中没有说出每个数值的大小，只侧重描述各项所在位上的数字，这在算筹布算上比较容易确定各项的数值，对于数目较小的开平方来说在算盘上实现也没有难度，但对于数目较大的开平方运算来说，可能会增加运算的难度。

严恭《通原算法》中的开平方新法，在运算过程中有“借一筭，步之，超一等”，古人在算盘上操作时可用心算替代这一步，如王文素《算学宝鉴》中的“平方商，觅根因，逆数常超一位寻。一定一兮百定十，万中商百记于心”[22]提供了证据。虽然《通原算法》中“借算”在后面的运算中一直参与运算，但因所取“借算”的值为1，后面每项乘以“借算”后，数值并未发生改变，所以这一步可以省略，在过渡到珠算开方时没有什么困难。该方法对每一步放置数字也都明确说明了具体数值，因此其余步骤亦均可在算盘上实现。但有唯一的缺点就是5层纵式布算，项数太多，如果要移植到算盘上需要在一横行上放置5项数据，这要求算盘的档位很多，且不利于观察，从而会使运算显得繁琐而容易混淆。

《算法统宗》中“诀”下开方法，也是一种异于传统布算的筹算开平方新法。类似的方法还见于更早的唐顺之(1507～1560)《武编》*郭一鹗为《武编》写的序言说：“得是编熟之化之，天下无勍敌矣!荆川先生熟而化此，以南剿倭、北创虏，十用其七八”[23]，似乎《武编》在唐顺之1555年复出参加抗倭[24]之前已成书。。书中针对营阵问题，有一个普遍性的开方法：

方营法：置积数为实，别置一算，为下法，从末常超一位定实。实上商置第一位得数，下法亦置上商，名曰方法。乃命上商除积，至尽而止。不尽，乃倍方法，为廉。于上商之次，续商第二位得数，廉法之次，照上商置隅。以廉、隅二法命上商除积，得尽而止。不尽，乃陪*“陪”通“倍”，或为“倍”之误[25]。隅法，并为廉。又于上商置第三位得数，廉法之次，照上置隅。以廉、隅二法，皆命上商，除积，至尽而止。不尽，如法命之。([23]，370～371页)

此法与《算法统宗》、《通原算法》的筹算开平方法相出入。书中还有一个算例([23]，374～375页)，更接近《算法统宗》的筹算开平方法。它们与元末明初算书中的筹算开平方新法都属于革新传统筹算开平方而成的新法，当有更早渊源，其产生可能也在元明之际或前后不远。5种大同小异的筹算开平方新法，说明在珠算逐渐流行开来的时代，对筹算开方的改革不是个别人的行为，而是一种趋势，正是这类筹算开平方新法为珠算开平方提供了基础。《算法统宗》中先有这种新法，之后给出珠算商除开平方法，说明两者有密切联系。后者具有以下特点：(1)不用“借算”一项；(2)布算分商、实、方三项(清初《算海说详》增加只列商、实两项的珠算开平方新法)；(3)商、实、方各项在运算过程中都没有进位(或退位)变化；(4)运算过程中的各项均有数值说明；(5)对其中涉及的乘法运算都用相应的九九口诀进行了说明；(6)先放置商数等项，再减积或减余积。其中(1)、(2)、(3)、(5)是区别于元末以前的传统筹算开平方法的特点，(1)、(2)、(3)、(4)是成熟的珠算商除开平方法必须具有的特点，(6)是现存珠算商除开平方法都具备的特点。而(1)、(2)、(3)、(5)在《算法全能集》、《丁巨算法》中的三层筹算开平方新法中已经具备，(3)、(4)、(5)、(6)在《通原算法》中的五层筹算开平方新法中已具备。传统筹算开平方法中则不具备这些特点。所以，珠算商除开平方法应该是从改革后的筹算开平方新法过渡而来。

现在要估计一下珠算归除开平方法和商除开平方法的时代。《算法统宗》、王肯堂《郁冈斋笔麈》(1602年自序)等介绍归除开方法时都说是新增此法，且都属于珠算归除开方法，说明此法产生不久。虽然目前所知，载有归除开立方法且已出版的最早算书是《算法统宗》[17]，但刊刻此书的1592年肯定不是此法产生的时间。朱载堉《算学新说》载有珠算归除开平方法，并说“夫算学之有书，其亦旧矣，谓之新说，何也？……平方不用商除，立方不显廉法之类，旧则繁而新则简”[26]。朱氏另一本著作《嘉量算经》(1610)中也称：“用归除开平方，各算书未载，是故详载之”[27]。两书都认为是他自己首先采用归除开方法的。《算学新说》虽刊于1603年，但《律学新说》(1584年序)卷2说“古所谓黄钟空围九分者，即算家所谓内周也。……自汉已来……至今莫觉其误。臣于《律书·周径》篇中论之详矣，除已见《律书》及《算学新说》，兹不复载”[28]，华印椿([1]，80页)、郭世荣和郭书春([5]，551页)、李培业[29]、劳汉生([7]，92页)等学者推测《算学新说》写于1584年。其实1584年并不是撰写此书的时间下限。戴念祖考证其成书不晚于公元1581年，不早于1567年[30]，则书中的归除开平方法的产生不晚于1581年。如考虑到书中的内容可能在成书之前，所以1567年也不一定是归除平方法的最早时代。但朱载堉生于1536年，到1550年才14岁，因此朱氏归除开平方法应该在1551～1581年之间，而很可能在16世纪六七十年代(24～43岁)。珠算归除开方法应该是将归除法和珠算商除开方法相结合发展起来的，所以珠算商除开平方法应该更早。鉴于顾应祥《测圆海镜分类释术》(1550)、《弧矢算术》(1552)、《测圆算术》(1553)中均载有珠算开带从方法，周述学《神道大编历宗算会》(1558)中除了载有珠算开带从方法还有珠算开三乘方法，我们估计珠算商除开平方法的产生不应晚于16世纪上半叶，而可能更早。有的学者认为王文素《算学宝鉴》已经有之，但我们不能肯定。无论如何，我们可以大致勾勒出从筹算开平方过渡到珠算开平方的大致脉络如下：

传统的筹算开平方——筹算开平方新法(《通原算法》所载的五层新法，《算法全能集》和《丁巨算法》所载的三层新法，《武编》中的三层和五层新法，《算法统宗》的五层新法等。这些书中的新法至少有部分源于更早的时代)——珠算商除开平方法——珠算归除开平方法。

6 结语

唐中叶以来为了简化计算，对筹算乘除法进行改进，主要表现在两个方面：一是化三层布算为一层或两层布算，二是化乘除为加减运算。([5]，400～401页)现存文献中，直到元末才有对传统筹算开方法的改进，实际的时间可能会早一些，书中的这些内容可能取自以前的著作。如在布算上，《算法全能集》和《丁巨算法》中的开平方新法，布算只有3层，没有“借算”，没有“方法”的退位(或进位)变化；明初《通原算法》的开平方法，布算多达5层，可能源自严恭早年收集的算书。这几种算书中的开方新法，在运算过程中都没有方法、廉法、隅法的退位变化。它们与后来的《算学宝鉴》、《武编》和《算法统宗》中的筹算开平方新法，反映了元后期以来筹算开平方改革在细节上具有多种可能，但它们的一个共同点是没有退位变化，这是筹算开平方走向珠算开平方的关键一步。

筹算开平方新法在对乘减运算过程的描述中都出现了九九口诀(有的带“呼”字)，详细列出各项相乘的先后顺序以说明开方过程中的乘减运算采用前乘法，这或许为了表明要区别于当时已经出现的后乘法，也可能仅仅方便读者掌握每一步运算程序。而现存算书中所记载的珠算开平方法也普遍有这一特点。

珠算开方法区别于筹算开方法的显著特点是，将用算筹从上至下排列各项的方式，改为在算盘上从左至右在一横行上排列各项。当没有明文说明所用算具时，如果有很明确的上下位置说明，或清楚地描述了某些项的退位变化，特别是有法(方、廉、隅)的退位变化，那么至少也可以确定开方的总体布局上是筹算，否则是珠算的可能性就很大了。

筹算开平方新法远比传统筹算开平方法更适合移植到算盘上用一行横式实现，其中三层新法尤其适合改造成珠算商除开平方法，其时间应不晚于16世纪上半叶，而可能更早。归除开平方法大约产生于16世纪六七十年代，朱载堉很可能是这一方法的首创者，或至少是一个先驱。从算理上讲，珠算开平方很可能经历了传统筹算开平方法到筹算开平方新法，到珠算商除开平方法，再到珠算归除开平方法的发展历程。

致谢本文修改稿吸收了审稿专家提出的宝贵意见，谨致谢忱。

1 华印椿. 中国珠算史稿[M]. 北京: 中国财政经济出版社, 1987. 396～397.

2 李迪. 中国数学史大系第6卷西夏金元明[M]. 北京: 北京师范大学出版社, 1999. 403.

3 韩祥临. 《算法统宗》与珠算[J]. 湖州师范学院学报, 1999, 21(6): 28～36.

4 山崎與右衛門, 戶谷清一, 鈴木久男. 珠算算法の歴史[M]. 東京: 森北出版株式会社, 1958. 438～440.

5 郭书春. 中国科学技术史·数学卷[M]. 北京: 科学出版社, 2010. 574.

6 李俨. 十三、十四世纪中国民间数学[M]. 北京: 科学出版社, 1957. 54～55.

7 劳汉生. 珠算与实用算术[M]. 石家庄: 河北科学技术出版社, 2000. 231～232.

8 邹大海. 透廉细草提要[M]//中国科学技术典籍通汇·数学卷. 第1分册. 郑州: 河南教育出版社, 1993. 1281.

9 滕艳辉. 《透廉细草》内容分析与评价[J]. 广西民族大学学报(自然科学版), 2010, 16(3): 26～28, 33.

10 永乐大典算法[M]//中国科学技术典籍通汇·数学卷. 第1分册. 郑州: 河南教育出版社, 1993. 1419～1420.

11 丁巨. 丁巨算法[M]//中国科学技术典籍通汇·数学卷. 第1分册. 郑州: 河南教育出版社, 1993. 1301.