基于流固耦合方法的漂浮塔柱式风力电站减振器设计

郭涛，朱磊，伍立说，兰剑

（中交疏浚技术装备国家工程研究中心有限公司，上海 201208）

我国可利用的海上风能储量占总储量的75%，约7.5×105MW。从发电经济性考虑，海上阻碍少，风力持续强劲，适合安装大型风力透平，是良好的风力发电场所。海上风力电站分为固定式与漂浮式两种，前者立在海底陆地上，一般安装在水深不超过80 m的近岸区域；后者无需海底固定，降低了建设成本，必要时还可以移动位置，是深水海域中风力电站的不二选择。目前日本等国在漂浮风电领域发展迅速，已走在世界前列[1]。但是漂浮式海上风力电站由于没有固定端，在不稳定风力、海面波浪力等外在激励下容易发生摇摆，可能影响叶片转动及发电机组的稳定运行。

调频振子阻尼（Tuned Mass Damper，以下简称TMD）[2]、调频液柱阻尼器（Tuned Liquid Column Damper，以下简称 TLCD）[3]、调频液体阻尼器（Tuned Liquid Damper，以下简称 TLD）[4]常作为内置的被动阻尼装置被用于楼宇、桥梁、海上浮台等大型建筑减振[4-6]，也被建议用于抑制海上漂浮电站摇摆[7]。其原理是通过调频共振从结构上吸收能量，并依靠振子阻尼后液体晃荡阻尼消耗能量。基于相似原理，一种将调频振子放在晃荡液体中的联合减振器[8-9]被提出，其同时具有TMD吸能作用稳定及TLD自身耗能效果显著的优势，本文将设计此类减振器并用于抑制悬浮塔柱式风力电站在涌浪作用下摇摆振动，通过数值计算预测减振效果并优化减振器，为漂浮式风力电站的减振设计提供思路。

1 物理模型

选择世界上首个漂浮式风力发电站——挪威国家石油海德罗公司于2009年在北海试运行的Hywind风力发电站作为减振对象的参考原型，见图1。该电站水上部分高65 m，水下部分约100 m，总重达5.3×106kg，叶片及发电机组部分重1.38×105kg，位于塔柱顶部。空心塔柱的主要材料为密度1 500 kg/m3的玻璃纤维，壁厚约为0.25 m。水下的圆柱式浮台直径为8.3 m，底部放入水和岩石当作压舱物，浮力柱通过3根锚链与海底固定。假设压舱物平均密度2 500 kg/m3，计算可得重心约在水下65 m处，锚链联接在重心附近以防止塔柱平移，电站塔柱绕重心扭转的转动惯量约为8.6 ×109kg·m2。

图1 Hywind风力发电站的基本结构（m）Fig.1 Basic structure of Hywind wind turbine station(m)

在发电机组运行时，常规风力缺乏周期性，其对塔柱的摇晃影响较小，周期相对稳定的涌浪是导致塔柱摇晃的主要因素。根据中国海浪环境预报中心发布的数据，我国沿海的海浪有效波高一般不超过5 m，周期在5 s左右。本文采用如下假设：

1）漂浮式风力发电机在6级海况以下条件时能够平稳运行，而在更恶劣天气及海况下停止运行。假设导致漂浮式电站摇晃的波浪为由6级海况风导致的单一波形涌浪，近似为Stokes二阶波，浪高5 m，周期5 s。

2）受海水的阻碍作用，电站塔柱的单次自由摇晃将在2个周期内平复，即塔柱自由扭转振动的阻尼比约为0.5。

图2给出了塔柱漂浮在水中时，浮力维持其稳定的受力示意图。塔柱的浮心位置高于重心，发生扭转偏移后，浮力将提供一个与扭转角度相反方向的扭矩使其回到竖直平衡位置。

图2 电站塔柱稳定漂浮的受力示意图Fig.2 Force schematic for stable floating of the station tower

将漂浮式电站塔柱简化为仅绕通过重心的水平轴扭转的单自由度刚体，采用Morison公式[10]初步估算波浪对竖直塔柱的作用力。

在塔柱扭转角度不大时，浮心在塔柱上的位置可认为保持不变、浮力大小仍等于重力，则浮力提供的力矩为：

式中：m、g为塔柱质量及重力加速度；yB、yG为浮心及重心的y方向坐标值；yB0、yG0为塔柱完全竖直，未发生偏转时的浮心及重心的y坐标值。

由式（1）可得，浮力提供的扭矩刚度系数KR约为7.8×108N·m/rad，假设海水提供的扭转振动阻尼比ξ约为0.5，则浮力扭矩的实际扭阻力系数C 可用式（2）计算，约为 2.59×109N·m·s/rad。

式中：JR为物体绕重心扭转的转动惯量，kg·m2。

在浮力矩的作用下，Hywind塔柱绕重心的固有扭转频率约为0.047 8 Hz，仅为涌浪激励频率的1/4左右。塔柱的固有频率与波浪的频率相差巨大，不会在任何波浪下发生共振扭转。其稳态受迫扭转的角位移滞后于激励扭矩的相位差可以通过下式计算：

式中：φ为滞后相位差，取值范围为 [0，π]；λ为激励频率与固有频率之比。

塔柱的稳态受迫扭转角幅值略小于0.007 rad，但由于扭转半径较大，位于塔顶的发电机组仍会发生幅值1 m左右的近似水平的摇晃，线加速度幅值约为1.4 m/s2。受迫扭转的角位移滞后于激励扭矩的相位差约为0.9π。

2 减振器的设计

塔柱顶部安装有发电机组，空间有限，若加装减振器，除成本较高、维护困难外，还将增加顶部设施的体积与表面积，同时使得电站重心明显上移，不利于塔柱扭振的衰减。基于安装调节方便、节约成本、维持塔柱外形等多方面考虑，选择将减振器设置在海平面附近的塔柱内腔中。塔柱内径约为7.8 m，当减振器为TMD时，扣除一定的安装、维护空间后，实际可用于安装调频振子的圆柱腔直径在6 m左右。为避免振子撞击塔柱壁面，振子的形状及许用振幅受限。为保证减振效果，可将多个减振器叠加使用。本文设计了TMD、TLD、联合减振器3种减振装置并进行了对比，具体构造见图3。

当减振器需要提供与激励波浪力矩方向相反的扭矩，即减振力矩与波浪力矩相位差约为π时，减振器性能达到最优。TMD及TLD的自由频率可由线性振动或驻波频率的理论公式进行预测，其优化设计可利用遗传算法、蚁群算法等多种搜索技术较快地确定最优的频率比及阻尼参数[11-12]；联合减振器内存在液体晃荡与壁面位移、振子振动相互作用的复杂耦合关系，仅靠理论或经验分析难以确定优化导向，需结合数值模拟结果及经验分析进行多次调试才能找到较优解。最终减振器的设计参数如下：

图3 3种减振器的构造示意图Fig.3 Structure sketches of 3 types of dampers

TMD：选用弹簧振子作为吸能部件，振子为底部边长1.12 m，高5.35 m的长方柱体，弹簧的水平刚度系数为9.33×104N/m，阻尼系数为5 880 N·s/m，振子的相对振幅不超过2.5 m。振子质量约为Hywind电站总质量的1%。

TLD：选择5.3 m底面边长，高1 m的空间为单个TLD空腔，内部充有0.6 m深的水，水的质量约为1.68×104kg。3个晃荡减振器竖向叠加约占用3.2 m的塔柱内高度，水质量约是电站总质量的0.95%。

联合减振器：TLD水箱中置入尺寸为0.9 m×5.3 m×0.4 m的钢制振子并充入0.56 m深的水。振子质量约为1.5×104kg，弹簧刚度系数约为2.78×104N/m，水质量约为1.57×104kg，振子的最大振幅不超过2 m，3个联合减振器的质量约为电站总质量的1.82%。

3 数值模拟方法及结果

减振器抑制涌浪导致的漂浮式风力发电站扭振的过程中，塔柱受到3种力：涌浪的冲击力，海水浮力及减振器的抑制力。当减振器为TLD时，还需考虑TLD内的液体晃荡；当减振器为联合减振器时，减振器内存在着振子-晃荡液体-减振器三者之间的耦合作用。数值计算中若考虑所有的耦合因素，计算资源消耗过大。考虑到减振器的设计、优化以数值结果为导向，需要多次模拟塔柱的减振过程，而本问题中对塔柱扭转运动最敏感的是减振器的响应；其次是波浪的运动，而海水的浮力、阻力则最容易预测，因此本文提出了一种兼顾精度与效率的求解策略（图4），具体如下：

1）将海水浮力与塔柱的耦合关系根据式（1）简化为线性的扭矩弹簧，将海水的阻尼作用根据式（2）简化为扭矩弹簧的扭阻力系数。

2） 将表征海水浮力的扭矩弹簧施加在塔柱上，考虑波浪变形与塔柱扭振的耦合作用而忽略减振器作用，求解波浪对塔柱的稳定周期作用力。

3）将周期的波浪作用力视为单向输入载荷，将海水浮力视为带阻尼的扭矩弹簧，数值求解此条件下电站塔柱与减振器的耦合响应。

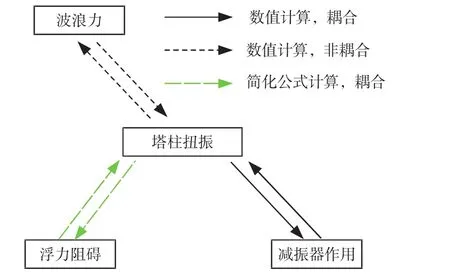
图4 数值计算塔柱摇摆过程中耦合关系的简化Fig.4 Simplified coupling relationship in numerical simulations for the vibration responses of the turbine tower

使用商用软件ANSYS Workbench内部模块分离求解并双向耦合的方法对该问题进行数值模拟，固体域用Mechanical模块按有限元法求解基于虚功原理的单元平衡矩阵方程式（4）；流体域的气-水两相流动使用CFX模块求解连续方程及Navier-Stokes方程式（5），两相共用同一流场及标准K-ε湍流模型，浮力效应通过密度差模型体现，两相体积分数rα及rβ满足式（6），采用连续表面张力模型计算气与水的自由界面并根据单元的体积权重进行界面光顺。

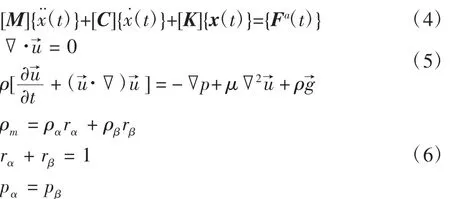
式中：[M]、[C]和[K]分别为质量矩阵、阻尼矩阵及刚度矩阵；{x（t）}及{Fa（t）}分别为时刻的节点位移向量及载荷向量；u、ρ、p、μ分别为流体速度矢量、密度、压力、黏性系数。在一个时间步内，两个求解器在流固交界面上多次传递流体压力与结构位移的计算结果来更新边界条件直至收敛，从而实现隐式精度。详细数值计算方法见文献[13]。

求解波浪对塔柱的作用力时，由于波浪运动的影响水深通常为波长的一半左右，且水平方向上5倍于塔柱直径外的流体区域对塔柱的影响较小，故选取42 m×42 m×40 m的区域作为计算域，其中水下部分28 m，水上12 m。用高24 m，直径8.3 m的刚性圆柱来表征塔柱，其位于计算域中央，水下部分20 m，水上8 m。此采用结构化网格划分计算域，网格总数为2 187 000，最小网格尺寸0.1 m。

按Stokes二阶波的波面方程式（7）给定计算域内两相分布。波上游为开口边界，水相速度由式（8）确定，气相速度为0；其它边界设置为开口压力边界，水相压力由式（9）决定，气相相对压力为0。当流体流出计算域时压力表现为背压，当流体流入计算域时，该压力为总压。圆柱仅具有绕质点水平扭转的自由度，重心位于水下65 m处，转动惯量为 8.6 × 109kg·m2。

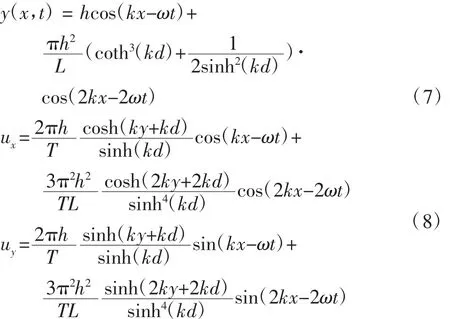
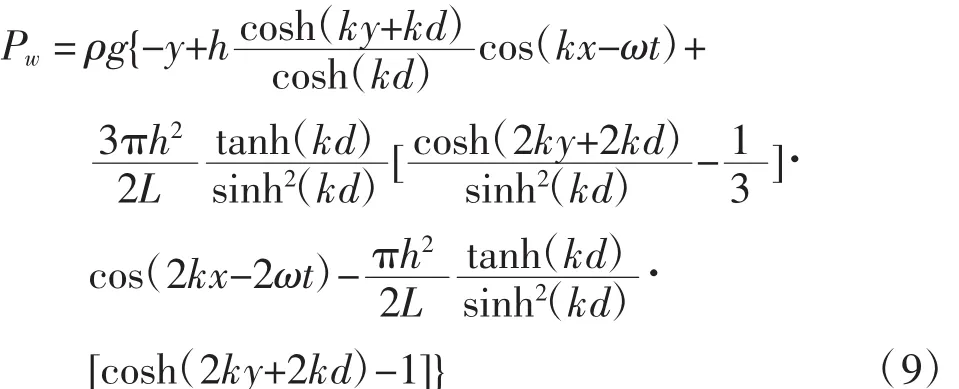
式中：x、y分别为波浪行进的水平方向及竖直方向；L为波长；h为波高；k为波数，定义为2π/L；ω为波浪角频率；d为水深；ux、uy分别为水质点的水平速度与竖直速度；Pw为波浪中的压力。

计算时间步长取0.062 5 s，为1个波浪周期的1/80。经过3个波浪周期后，波浪对塔柱的作用力有了基本稳定的周期性变化，图5给出了数值结果与Morison公式计算得到的波浪力对比。由图中可见，尽管波浪力的数值解与Morison公式解幅值上相近，但变化规律有差异，其在正向幅值上略有增大而在负向力上更加平缓。这是因为数值计算中考虑了柱体的摇晃以及阻碍波浪后造成柱体周围的水质点粒子的运动变化，理论上预测精度更高。

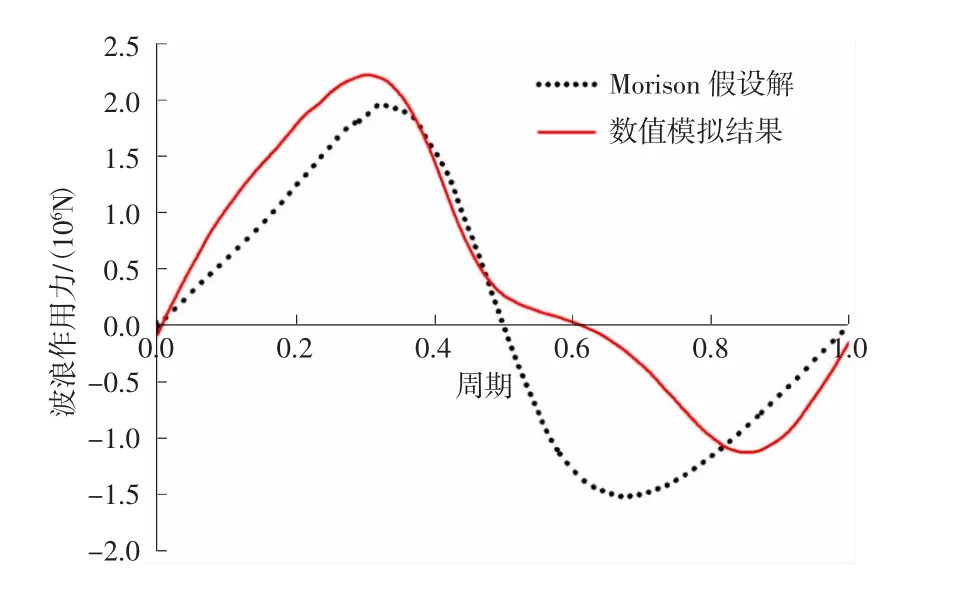
图5 波浪力的Morison公式解与数值计算结果比较Fig.5 Comparison between the wave force results from the Morison formula and the numerical simulation

计算减振器抑制塔柱的扭转振动时，波浪力的数值解作为周期性载荷加载在塔柱的海平面高度处，减振器内的水面晃荡、振子位移以及晃荡水与弹簧振子间的耦合作用同样使用上文介绍的数值方法求解。初始时刻，塔柱完全直立，减振器处于平衡状态，波浪力为0并逐渐增大。计算总时长为30 s，时间步长为0.062 5 s。

图6给出了联合减振器抑振过程中晃荡水及振子对塔柱的作用力。由图可见，联合减振器中，水的作用力因为振子激励及自身晃荡而具有双峰值的倾向，但仍与振子作用力在数值及相位上基本保持一致，与波浪提供的激励力保持接近π的相位差。这说明振子与晃荡水对塔柱的作用力方向始终与波浪力相反并阻碍着塔柱的受迫扭转振动。由于减振力是扭振剧烈程度的被动响应，减振力在扭振开始阶段较小，随后增大到理论幅值，在20 s后略有减小，是柱体扭转振动受到减振器抑制后振幅下降造成的。TLD、TMD独立减振时，晃荡水与振子作用力与波浪力的相位差同样为π；在幅值方面，振子作用力相比联合减振器略有增加，晃荡水的力则略有减小。

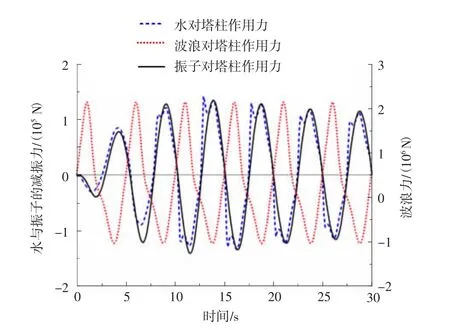
图6 联合减振器抑振时水与振子对塔柱的作用力Fig.6 Water and oscillator force on the tower during the combined damper suppressing vibration

图7对比了3种减振器分别抑制电站扭振时塔柱偏转角度的变化。由图可见，TLD、TMD、联合减振器分别使塔柱扭转角度幅值衰减了约8%、11%、17%。虽然在相同的调频质量下，TMD相比TLD具有更优秀的减振效果，但是TMD需要设置满足刚度要求的弹簧以及系统阻尼，成本较高，且其占用的塔柱内的空间最大；在空间相同的情况下，其抑振能力可能还弱于TLD；TLD设置简单，成本低廉，但单位质量的减振效果相对较差。联合减振器在两者间取得了平衡，其无需添加系统阻尼，仅需要满足刚度要求的弹簧，成本较低，最大的优势在于减振器内振子与水可以混合安置，且振子、水的抑振能力并不会比TMD、TLD有明显削弱，从而在相同的空间中提供了最大程度的减振效果。在减振器体积相同时，其减振能力约是TLD的2倍或TMD的1.5倍。

图7 3种减振器抑制塔柱扭转角位移的幅度对比Fig.7 Angular displacement of the tower suppressed by 3 types of dampers

4 结语

本文使用流固耦合数值方法求解了涌浪、海水、漂浮电站塔柱、减振器之间的相互作用过程，设计了3种减振器方案并通过数值预测减振效果的方式改进减振方案，使其减振效果达到了同类减振器的较高水平，并得到结论如下：

1）TMD、TLD、联合减振器均可抑制涌浪作用下漂浮电站塔柱的扭转振动，在水平面附近的发电站塔柱内安装约1%发电站质量的减振质量时，TLD可以削弱8%的扭转角幅值，TMD可以削弱约11%的幅度但需要占用更多的空间。联合减振器则可在与TLD相同的空间内安装约1.8%发电站质量的减振质量，达到17%的振幅衰减。

2）TMD单位质量的减振效果好，但成本高，占用空间大；晃荡TLD设置简单，成本低廉，但单位质量的减振效果较差。联合减振器综合了弹簧振子便于调整相位关系、晃荡液体成本较低的优势，在相似减振空间、相似费用条件下具有更好的减振效果。

3） 数值计算中对发电站柱体所受的波浪载荷、结构参数、振动形式、耦合关系等都进行了一定的简化和假设。实际设计中需要更进一步细化参数并提高耦合计算精度。

参考文献：

[1] 伍绍博，尹海卿，张开华，等.日本漂浮式风电技术现状及未来发展方向[J].中国港湾建设，2017，37（6）：108-114.WU Shao-bo,YIN Hai-qing,ZHANG Kai-hua,et al.Status and future development direction of Japan floating wind turbine theology[J].China Harbour Engineering,2017,37(6):108-114.

[2]MCNAMARA R J.Tuned mass dampers for buildings[J].Journal of the Structural Division,1977,1(9):1 785-1 798.

[3] HAYAMA S,IWABUCHI M.A study on the suppression of sloshing in a liquid tank:1st report,suppression of slosing by means of a reversed U-tube[J].Bulletin of JSME,1986,29(252):1 834-1 841.

[4] FUJINO Y,SUN L,PACHECO B M,et al.Tuned liquid damper(TLD)for suppressing horizontal motion of structures[J].Journal of Engineering Mechanics,1992,118(10):2 017-2 030.

[5] 文永奎，孙利民．大跨度斜拉桥钢塔施工阶段制振用TMD、TLD装置及其性能试验[J].地震工程与工程振动，2008，28（3）：157-164.WEN Yong-kui,SUN Li-min.TMD,TLD and performance tests for vibration control of steel tower of large span cable-stayed bridge during construction[J].Journal of Earthquake Engineering and Engineering Vibration,2008,28(3):157-164.

[6] MIN K W,KIM J,KIM Y W.Design and test of tuned liquid mass dampers for attenuation of the wind responses of a full scale building[J].Smart Materials and Structures,2014,23(4):494-501.

[7] RODERICK C.Vibration reduction of offshore wind turbine using tuned liquid column dampers[D].Amherst:University of Massachusetts Amherst,2012.

[8] 汪正兴，王波，钟继卫，等.液体质量双调谐减振器（TLMD）研究与应用[J].桥梁建设，2011（1）：10-13．WANG Zheng-xing,WANG Bo,ZHONG Ji-wei,et al.Research and application of tuned liquid and mass damper(TLMD)[J].Bridge Construction,2011(1):10-13．

[9] 郭涛，管志成，孙光普，等.调频振子-液体联合水平减振的流固耦合机理研究[J].西安交通大学学报，2016，50（1）：28-33.GUO Tao,GUAN Zhi-cheng,SUN Guang-pu,et al.Fluidstructure interaction analysis of vibration suppression by tuned oscillator-liquid combined system[J].Journal of Xi'an Jiaotong University,2016,50(1):28-33.

[10]MORISON J R,JOHNSON J W,SCHAAF S.The force exerted by surface waves on piles[J].Journal of Petroleum Technology,1950,2(5):149-154.

[11]MARANO G C,GRECO R,CHIAIA B.A comparison between different optimization criteria for tuned mass dampers design[J].Journal of Sound and Vibration,2010,329(23):4 880-4 890.

[12]BEKDAS G,NIGDELI S M.Metaheuristic based optimization of tuned mass dampers under earthquake excitation by considering soil-structure interaction[J].Soil Dynamics & Earthquake Engineering,2017,92:443-4611.

[13]GUO Tao,YE Yang-hui,LI Guo-jun.On the key parameters of an interior sloshing absorber for vibration suppression[J].International Journal of Structural Stability and Dynamics,2015,15(1).