三峡升船机塔柱结构运行期有限元分析

崔 建 华苏 海 东

(1.长江科学院 材料与结构研究所,湖北 武汉 430010； 2．水利部水工程安全与病害防治工程技术研究中心，湖北 武汉 430010)

1 研究背景

三峡升船机已进入通航阶段，主要用于为客货轮和特种船舶提供翻越三峡大坝的快速过坝通道，提高枢纽的通航能力。其设计过船规模为3 000 t级，最大提升高度为113 m，是世界上提升高度最高、提升重量最大的升船机。相对常规塔柱而言，三峡升船机塔柱由于爬升形式改变，不仅使单个塔柱在平面内的形式变得复杂，而且沿高程增加的诸多联系梁使得结构的形式及其受力分析更加复杂[1-4]。温度荷载是升船机塔柱结构的主要荷载之一，在运行期，齿条和螺母柱要适应年气温变化作用下的塔柱结构整体变形，正确估计塔柱结构在温度作用下的变形和应力，对齿轮齿条爬升式升船机方案的机构设计非常重要。同时，考虑到三峡升船机塔柱主要由薄壁结构组成，对外界气温变化极为敏感，受气温骤降及日照作用，薄壁的内外会形成较大的温度梯度，从而引起较大的温度变形及温度应力[5]。此外，混凝土内部湿度变化引起混凝土的干缩变形，由于塔柱结构表面积与体积之比要比大体积混凝土大得多，水分的散发量和散发速度相对要大而快，干缩变形对塔柱结构关键部位(齿条、螺母柱)垂直向变位的影响值得关注。因此，运行期塔柱结构状态、气温骤降、日照作用以及混凝土干缩对塔柱结构的影响均需要仔细研究。

本文采用长江科学院自主开发的模拟大体积混凝土建造及运行过程的温度场及温度应力仿真计算软件3DCRCPCG，对塔柱结构的施工浇筑全过程进行三维有限元温度应力仿真计算，研究其在运行期的温度应力和变形。在仿真计算中，考虑了混凝土的热学、力学性能、徐变以及温度边界条件等随时间的变化。

2 数值模拟

2.1 计算模型

三峡升船机塔柱为薄壁承重结构，建筑高度148.0 m，最薄壁厚1.0 m。顺水流向总长119.0 m、宽57.8 m，建基面高程47.5 m，底板厚度为2.5 m。塔柱两侧高程84 m处连接地表面，高程84 m以下部分被覆盖。结构在水平面内呈双重对称布置，结构模型示意见图1(a)。图1(b)俯视图中标示了水流方向，以水流方向为准，面朝下游，向左侧依次为左前塔柱、左后塔柱，右侧依次为右前塔柱、右后塔柱。

进行结构施工过程温度应力计算及气温骤降分析时，考虑到结构以及荷载的对称性，以垂直升船机的右侧前塔柱作为计算对象，采用1/4模型，见图1(c)。节点数为414 671，单元数为328 864。为提高计算精度，墙体1 m厚范围划分4层网格。

进行日照分析时，考虑到斜日照荷载的不对称性，采用整体模型进行计算，见图1(d)，为模拟日照影响，网格划分较密，表层30 cm范围网格大小为10 cm。模型共划分单元数487 116，节点数595 305。

基础模拟范围在上、下游方向及深度方向均为1倍坝高。顺水流向为X轴，指向下游为正，横河向为Y轴，指向左岸为正，竖直向为Z轴，向上为正。

图1 升船机塔柱结构布置(图中红点、黄点分别为螺母柱、齿条位置)Fig.1 Arrangement diagram of shiplift tower structure (red and yellow dots are respectively nut column and rack)

2.2 计算软件

3DCRCPCG软件包括温度场计算程序、温度应力计算程序和配套的前后处理程序，采用FORTRAN语言编写而成，具有计算速度快、精度高等优点[6-7]。在仿真计算中可模拟建筑物建造过程、混凝土通水冷却及保温情况，考虑自生体积变形、徐变、热学性能和边界条件随时间变化以及结构荷载和接触问题等因素。温度场和温度应力计算程序是相互独立的，先计算温度场，后计算温度应力。在温度场的计算中对时间的离散采用向后差分的隐式差分法，在温度应力的计算中采用初应变法计及徐变的影响。方程组的求解采用对称逐步超松弛预处理共轭梯度法的改进迭代格式和超级元两种快速算法。前处理程序是通过读入少量的数据生成有限元程序所需的坐标、单元节点编号、气温边界、约束条件和初始温度等数据。后处理程序是从整体结构中选取局部区域、剖面或结构边界的某些时间的计算成果，并形成引进的和自行开发的可视化和绘图程序所需的输入数据文件。该软件已经在三峡、丹江口、乌东德等大型工程的温度应力计算课题中应用，并取得了有效的计算成果。

2.3 边界条件

温度计算时，塔柱外侧高程84 m处连接地表面，高程84 m以下部分被覆盖，故塔柱外侧高程84 m以下部分为绝热面，其余部位均考虑为与空气接触，按第三类边界条件处理，放热系数β取15 W/(m2·℃)，基岩四周及底部按绝热处理。应力计算时，基岩底面取全约束，两侧面及下游面取法向约束，上游面不约束。三峡气象站1999～2005年实测平均气温见表1，根据表中数据，得到拟合曲线：

式中，Tc(t)为气温，℃；t为计算时刻至1月1日的时间，d。

根据试算结果，在顶板浇筑之后，塔柱筒体内表面(空腔内部)年变幅稍小，内部温度滞后于外部温度变化约1个月，故运行期塔柱筒体内采用的内部温度曲线为

表1 三峡气象站1999～2005年平均气温Tab.1 Average temperature of the Three Gorgesmeteorological station in 1999～2005 ℃

2.4 混凝土热学和力学参数

根据长江科学院的试验报告[8]，混凝土热学和力学性能参数见表2。塔柱运行期，混凝土水化热已释放完毕，温度随气温变化，故运行期不考虑混凝土绝热温升。基础弹性模量为30 GPa，各分区混凝土弹性模量采用如下拟合表达式E(t)=E0(1-e-AtB)，其中，E0为混凝土最终弹性模量，GPa；t为混凝土龄期，d，拟合系数见表3。气温骤降、日照计算时，各部位弹性模量取值见表4。

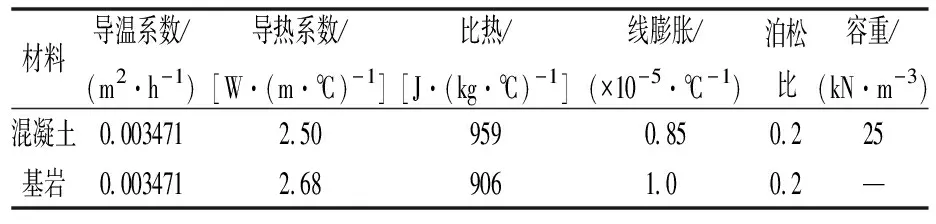
表2 混凝土热学性能Tab.2 Thermal properties of concrete

表3 各分区混凝土弹性模量拟合系数Tab.3 Fitting coefficient of concrete elastic modulus

表4 计算气温骤降、日照时的弹模取值Tab.4 Elastic modulus under temperature drop and sunshine GPa

2.5 混凝土徐变

在进行气温骤降及日照计算时，由于历时较短，不考虑混凝土徐变。在温度应力仿真计算中，考虑混凝土徐变变形的影响，采取的表达式如下

C(t，τ)=C1(τ)[1-e-k1(t-τ)]+C2(τ)[1-e-k2(t-τ)]

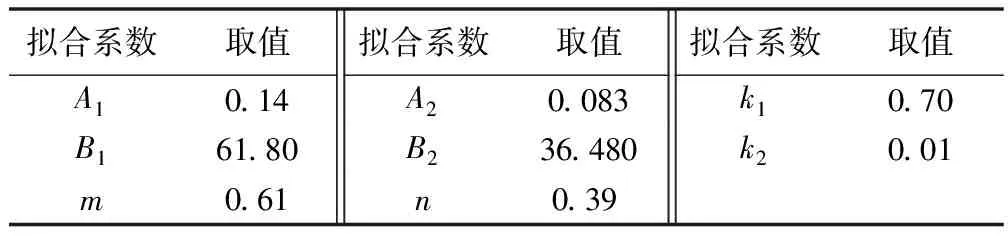
表5 徐变表达式拟合系数Tab.5 Fitting coefficient of creep expression

2.6 气温骤降资料

模拟气温骤降的温度场及温度应力计算中，首先在年气温变化条件下计算20 a时长直至气温骤降发生，以此作为初始温度场。再以气温骤降数据作为筒体外边界温度条件进行计算，得到气温骤降时的温度场，以此为荷载进行应力计算。气温骤降全年统计见表6，三峡坝区正常运行期2月实测的2～3 d最大降温值为15.6℃，考虑单天最大降温值，计算中按2 d降幅分别取为10℃，5.6℃。

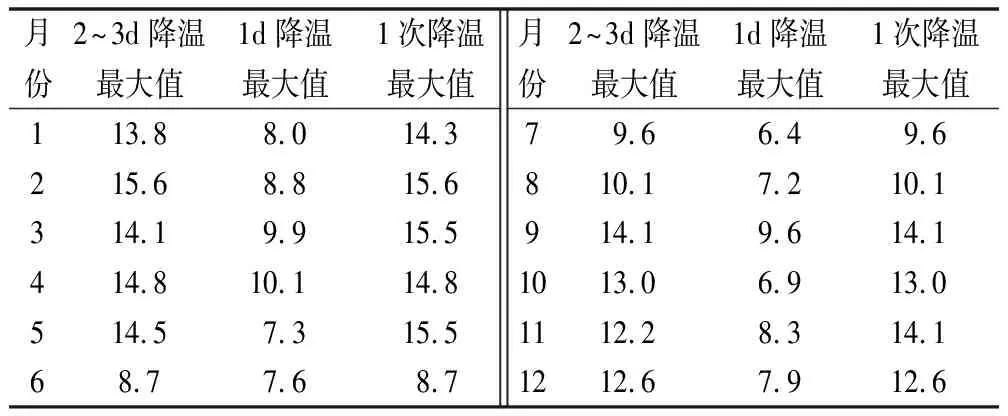
表6 气温骤降全年统计Tab.6 Annual statistics of temperature drop ℃

2.7 日照作用

日照作用计算分正日照与斜日照2种情况考虑。正日照指仅正面受太阳幅射，斜日照指正面与一侧面同时受太阳的幅射。考虑到塔柱两侧高程84 m以下部分被覆盖，基本不受日照影响，故正日照作用范围为右侧塔柱高程84 m以上外表面及左侧塔柱航槽侧高程140 m以上表面；斜日照作用范围为塔柱下游侧、右侧塔柱高程84 m以上外表面及左侧后塔柱航槽侧表面。此次计算未考虑顶部日照。由长江科学院日照试验资料[9]可知，向阳面与背阳面表面温度分别为26.8℃和6.7℃，影响深度取为30 cm，见图2，日照工况见表7。

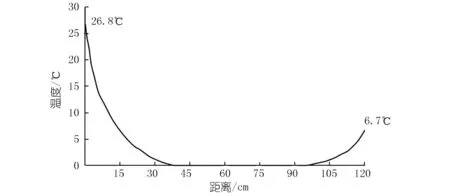
图2 日照作用实测温度分布曲线[9]Fig.2 Measured temperature distribution curve of sunshine action

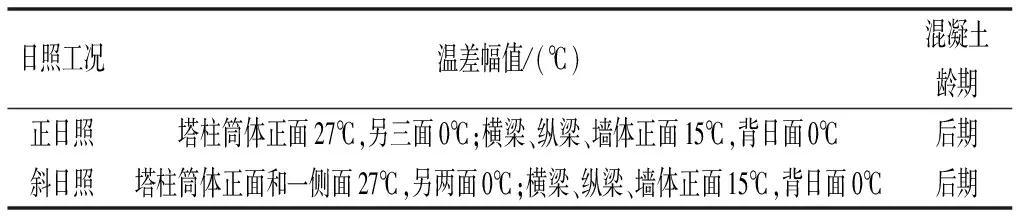
日照工况温差幅值/(℃)混凝土龄期正日照塔柱筒体正面27℃,另三面0℃;横梁、纵梁、墙体正面15℃,背日面0℃后期斜日照塔柱筒体正面和一侧面27℃,另两面0℃;横梁、纵梁、墙体正面15℃,背日面0℃后期

2.8 混凝土干缩

混凝土的干缩变形主要是由混凝土内部湿度变化引起的。因此精确计算混凝土湿度场是计算干缩变形的关键。混凝土内部湿度分布满足湿度扩散方程

式中,C(x,y,z,t)为湿度含量，定义为混凝土当前含水量与可蒸发水总量的比值，完全干燥时C=0%；含水量等于可蒸发水量时C=100%。kc为湿度扩散系数，它与混凝土材料性质有关，同时又与湿度大小有关。对于升船机进行湿度场仿真模拟计算，初始湿度场C(x,y,z,t0)=C0(x,y,z,t0)，C0为混凝土的初始湿度值，取100%。湿度扩散系数kc在等温条件下可表达成湿度C的函数[10]：

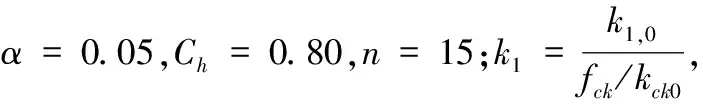
湿度场和干缩变形的计算对于网格密度的要求较高，不便于进行塔柱整体模型的计算。为此，采用平面模型分析结构在垂直向的干缩变位，见图3。取与塔柱等高、宽度为1 m(模拟墙体厚度)的细长方形模型为计算对象。主要模拟沿宽度方向的湿度变化(即墙体两侧与空气接触)所带来的沿高度方向的收缩变形，空气湿度取为75%。在变形计算中，细长方形的底部全约束。干缩和湿度之间的关系按Δεsh=αshΔC计算，其中Δεsh为收缩应变增量，ΔC为湿度增量，αsh为干缩系数取1.5×10-3。

图3 湿度场和干缩变形的网格示意Fig.3 Meshes diagram of humidity fieldand dry-shrinkage deformation

3 结果与分析

3.1 运行期塔柱结构状态

3.1.1温度场

考虑到结构以及荷载的对称性，进行结构温度及应力仿真计算时，采用1/4模型，以垂直升船机的右侧前塔柱作为分析对象，见图1(c)。计算结果表明，结构的温度场在84 m以上各高程的分布基本相同，以高程118 m典型水平剖面为例，图4给出了筒体在运行期冬季、夏季的温度分布图。可知，冬季筒体温度在6℃～10℃之间，夏季筒体温度在25℃～28℃之间，筒体内外温差不大。从夏季到冬季，内部变化值约17℃，外部变化值约为21℃。

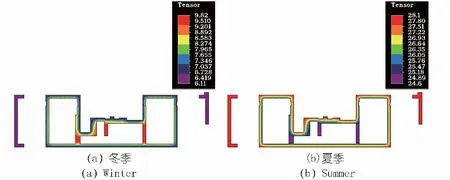
图4 运行期冬季、夏季筒体温度分布(单位：℃)Fig.4 Temperature distribution of ship lift tower inwinter and summer operation period

3.1.2变 形

图5为运行期夏季至冬季塔柱结构相对变形图。塔体变形呈现出随年气温周期性变化而变化的规律。从夏季到冬季，塔柱结构总体呈收缩变形，其中竖直向下变形最大，顶部达到25.1 mm，顺流向位移在上游侧约为10 mm，横河向位移在右塔柱外侧约为5 mm。

图5 从夏季到冬季结构位移(单位：mm)Fig.5 Structural displacement from summer to winter

3.1.3应 力

顺流向应力方面，筒体下部约束区有约2 MPa的拉应力，筒体其它部位应力水平不高。横河向应力方面，筒体本身应力水平不高，夏季至冬季温度变化引起的塔柱左右联系梁的横河向最大拉应力约为0.36 MPa，表明年气温变化引起的塔柱联系梁横河向应力不大。竖直向应力基本为压应力，压应力最大约为6 MPa，位于筒体下部外侧面。

3.2 气温骤降的影响

气温骤降至最低温(外界气温为-7.2℃)时，筒体表面温度在-2.9℃左右，筒体内温度则为7℃～9℃，相比降温前，表面温度变化约11.3℃，表面附近温度梯度较大。此时塔柱顺流向位移基本向结构中部收缩，最大值在上游侧顶部，约为4.2 mm；横河向位移，外侧墙由下至上依次增大，最大位移位于顶部，约2.3 mm；竖直向位移，从下至上依次增大，筒体顶部竖直向位移达到4.4 mm。此时塔柱顺流向底板表面拉应力约为3.0 MPa，影响深度1 m左右，筒体外表面拉应力约为2.4 MPa；横河向底板表面拉应力约为2.6 MPa；竖直向筒体结构外表面基本处于受拉状态，应力在2.5 MPa左右。

气温骤降作用时齿条、螺母柱部位的位移沿高程分布见图6。由图可知，齿条、螺母柱竖直向收缩，位移最大值均位于顶部，从下至上呈线性分布，最大值分别为3.8，3.9 mm。顺流向位移、横河向位移最大值也基本位于结构上部，齿条部位两方向的最大位移分别为0.83，1.32 mm，螺母柱部位两向的最大位移分别为1.09，1.77 mm。

图6 气温骤降时齿条、螺母柱部位位移沿高程分布Fig.6 Displacement distribution of rack and nut columnalong the elevation under temperature drops

3.3 日照作用的影响

3.3.1正日照对塔柱结构变形的影响

受表面升温的影响，塔柱在顺流向、竖直向变形均表现为膨胀作用(见图7)。顺流向位移变形规律为上游侧向上游位移，下游侧向下游位移，沿高程由下至上，位移量依次增大，最大位移约0.97 mm；横河向位移在塔柱右侧面中间部分向外变形，最大值约1.4 mm，在上、下游顶部较大，右侧塔柱最大位移为3.2 mm，左侧塔柱最大位移为2.7 mm，塔柱顶部高程位移基本为横河向正向，变形量约为2.2 mm；竖直向位移变形规律基本是向上方向的变形，沿高程由下至上位移量依次增大，筒体部位上方变形量最大值约1.6 mm。

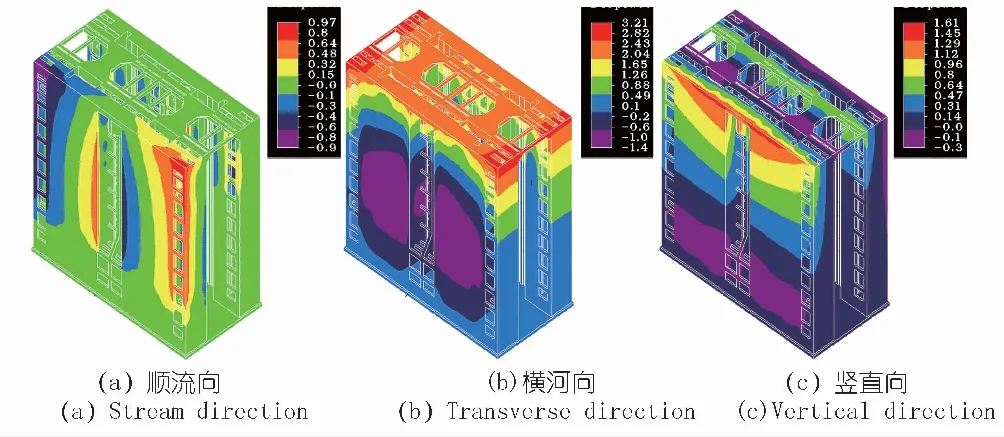
图7 正日照塔柱结构位移(单位：mm)Fig.7 Structural displacement of ship lift towerunder normal sunlight

3.3.2斜日照对塔柱结构变形的影响

对于顺流向位移，结构表面表现为膨胀作用，但由于下游侧也受到日照作用，所以上下游塔柱变形不具有对称性：下游面中部向下游变形而外拱，下游侧顶部向下游侧的位移比正日照时有所减小，顶点向上游位移为1.27 mm。对于横河向位移，塔柱右侧面(日照面)中间部分向外变形，最大值约1.3 mm，横河向位移以左侧塔柱下游外侧顶部最大，约为3.6 mm，右侧塔柱最大位移则为2.96 mm。受日照面在竖直向表现为膨胀作用，沿高程由下至上，位移量逐渐增大；受下游面升温影响，下游侧塔柱的竖向位移增大，筒体部位上方变形量最大，达到1.77～1.86 mm，见图8。

3.3.3日照对齿条螺母柱变形的影响

图9～10给出了正日照、斜日照作用下齿条、螺母柱部位位移沿高程方向分布。齿条部位，正日照横河向最大位移为1.43 mm，斜日照最大值为1.38 mm，均发生在高程120 m处，主要是由于升温导致结构中部外拱所致。同时，受温升影响结构向上位移，数值在0.4 mm以下。螺母柱部位位移与齿条部位规律一致，横河向最大位移为1.05 mm，竖直向位移在0.4 mm以下。由以上结果可知，日照作用在齿条、螺母柱部位引起的位移较小。

图9 日照作用时齿条部位位移沿高程方向分布Fig.9 Displacement distribution of rackalong the elevation under sunlight

3.4 混凝土干缩的影响

如2.8节所述，在混凝土初始湿度值取100%，空气湿度值取75%的计算条件下，进行长达40 a的湿度场及干缩位移变形计算。图11为不同干燥龄期的塔柱混凝土内部湿度分布图。由图11可知，塔柱混凝土湿度的传导是非常缓慢的。经过2个月后湿度有约10%变幅的区域仅限于表层4 cm，6个月后约为7 cm，1 a后约为10 cm；深度为25 cm处的混凝土2 a后的湿度变化减少量约为4%，5 a后的湿度变化减少量约为8%，10 a后的湿度变化减少量约为13%，20 a后的湿度变化减少量约为17%。塔柱混凝土中心处的湿度5 a的变化减少量约4%，10 a的变化减少量约9%，20 a的变化减少量约15%；40 a的塔柱内部湿度场接近于80%，湿度场基本趋于稳定。离塔柱混凝土表面越深，湿度变化速率越小。虽然混凝土湿度传导很慢，但在塔柱混凝土干燥期的前5 a，表面区域湿度场的变化较大，塔柱内外出现较大的湿度差，这种较大的湿度差易产生表面拉应力，从而引起表面裂缝。

图10 日照作用时螺母柱部位位移沿高程方向分布Fig.10 Displacement distribution of nut columnalong the elevation under sunlight

图12为塔柱不同部位垂直向位移变化曲线。由图可知，塔柱顶部位移最大，40 a后塔柱顶部位移约-4.2 cm(负号表示收缩变形)；在塔柱混凝土干燥的早期，位移的变化幅度较大，这是因为混凝土表面湿度变化较快，从而引起了较大的湿度变形。到了塔柱混凝土干燥的后期，塔柱位移变幅逐渐减小直至稳定。

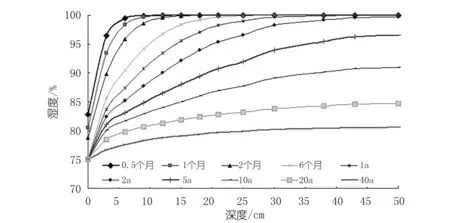
图11 不同干燥龄期的塔柱混凝土内部湿度分布Fig.11 Internal humidity distribution of towerconcrete at different dry ages

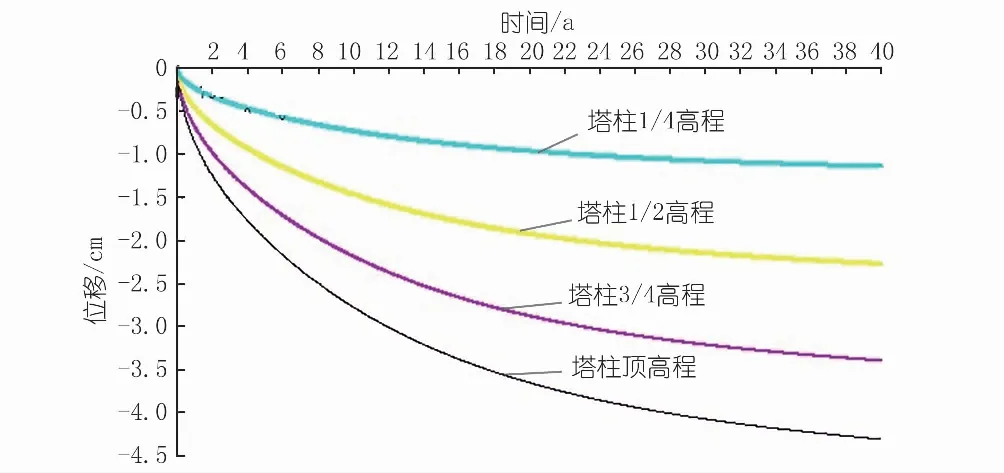
图12 塔柱不同部位位移变化曲线Fig.12 Displacement variation curve of towercolumn at different positions

4 结 论

(1) 运行期各季节塔柱筒体内外温差不大，变形随年气温周期性变化而变化，各方向应力水平不高，最大值在2 MPa以内。

(2) 气温骤降引起塔柱结构顺流向、横河向、竖直向3个方向的位移最大值分别约为4.2,2.3,4.4 mm，底板及筒体3个方向的应力最大值约3.0,2.6,2.5 MPa；齿条、螺母柱3个方向的位移最大值约4.0,1.1,1.8 mm。

(3) 在正日照和斜日照作用下，塔柱结构均表现为膨胀现象，其中斜日照作用下塔体变形量略大一些，在齿条、螺母柱部位引起的位移较小。

(4) 塔柱混凝土湿度的传导非常缓慢，在混凝土初始湿度值取100%，空气湿度值取75%的计算条件下，计算至第40年，塔柱内部湿度场接近于80%，湿度场基本趋于稳定。离塔柱混凝土表面越深，湿度变化速率越小。在塔柱混凝土干燥的早期，混凝土表面湿度变化较快，从而引起了较大的湿度变形，塔柱位移的变化幅度较大，而后期位移变幅逐渐减小直至稳定。