一种开关磁阻电动机瞬时转矩在线估算方法

陈海进，李锦阳

(南通大学，南通 226019)

0 引 言

开关磁阻电动机(以下简称SRM)具有结构简单、价格低廉、调速范围广、可靠性高等一系列优点，在工业应用中越来越受到青睐。但由于其工作磁路饱和、磁滞效应和涡流等因素产生的非线性特性，很难对其进行精确而快速的建模[1]，从而很难获得精确的磁链和转矩等参数。然而瞬时转矩大小的获取对SRM瞬时转矩控制及转矩脉动的抑制等具有重要作用，因此有必要对转矩测量估算技术进行研究。文献[2]搭建了SRM转矩测试系统实验平台，使用扭矩传感器直接测量转矩，这种方法虽直接方便，但扭矩传感器既复杂昂贵又增大了系统的体积。文献[3-4]分别使用BP神经网络和模糊神经网络对SRM的转矩特性建模，以获得转矩与相电流及位置角之间的映射关系，之后通过测量相电流和位置角获取瞬态转矩。神经网络建模虽具有较强的鲁棒性和自适应性，但对处理器要求较高。其次，文献[3]的训练样本使用的是MATLAB中的SRM电机模型，实用性不足。文献[4]的训练样本通过实测电机的静态转矩特性获得，此过程除了需要扭矩传感器，还需要位置传感器和转子夹紧装置来将转子固定在特定位置，不仅耗费额外空间，增加了系统复杂度，而且在转矩较大时夹紧装置很难保持转子绝对静止。文献[5]通过函数拟合法来表示转矩与相电流及位置角的关系，将测量到的相电流与位置角信号输入PC机计算出瞬时转矩，该文将某相转矩近似地表示为磁链对位置角的偏导数与电流的乘积，此处会具有相当的误差；其次实时测量时需要PC机进行计算，相对于以微控制器为核心的控制系统，系统体积和成本大大提高。

本文提出了一种基于微控制器的瞬时转矩在线估算方法，无需转子夹紧装置和位置传感器即可获取电机的转矩特性，电机运转时通过测量相电流和位置角估算瞬时转矩。

1 技术方案

1.1 转矩估算原理

该方法是通过实时测量每一相的电流和位置角，然后根据转矩特性表使用双线性插值法计算得到一相转矩，将所有相的瞬时转矩相加即得到该时刻电机的合成转矩。以实验所用的三相12/8 SRM为例，测量方法如图1所示。

图1 转矩测量方法示意图

由图1可知，转矩特性表是估算三相转矩的前提，因此需先获取转矩特性。

1.2 转矩特性的获取

1.2.1 原理

电机的转矩特性可由磁链特性计算得到，因此在不使用扭矩传感器时需先获取磁链特性。不考虑互感、涡流和磁滞效应的影响，处于某个位置θ*的一相绕组磁链可以由下式计算得到：

(1)

式中：t*和i*分别是对应位置角为θ*的时刻和相电流；u(t)和i(t)分别是该相t时刻的电压和电流；ψ(0)是0时刻的磁链值，由于0时刻无电流而为0；R是该相绕组电阻。R会随温度而变化，实验时需要在线测量，使用如下算法：

(2)

式中：tc是一个电气周期内电流归零的时刻。为了用采样得到的电压电流数据计算磁链，式(1)可以根据梯形积分公式改写为离散形式[6]：

R[i(p)+i(p-1)]}+ψ(0)

(3)

式中：Δt为采样间隔，索引p对应时间t*且索引0对应0时刻。根据式(3)即可求得某个位置θ*的磁链。

由磁阻最小原理可知，当定子某相绕组通电时，所产生的的磁场由于磁力线扭曲而产生切向磁拉力，试图使相近的转子旋转至其轴线与该定子轴线对齐的位置，即磁阻最小位置。因此根据各相对称的特点，通过给不同相通电，可以使三相12/8电机一相转子分别稳定在4个不同位置，施加电压激励从而测得4条电压电流离散曲线。由式(3)，可将其转换为磁链-电流离散曲线。再对离散曲线进行插值计算，即可获得4个位置下测量范围内任意电流值对应的磁链值。由于磁链与位置角的关系是一个周期性的波形，因此可以用傅里叶级数来表示。文献[7]使用三阶傅里叶级数来表示磁链与位置角的关系，而实验所用三相12/8电机可以获得4个位置下的磁链特性曲线，因此可以提高精度，使用四阶傅里叶级数表示电流为i*时任意位置的磁链：

ψ(i*,θ)=ψ0(i*)+ψ1(i*)cos(Nθ)+

ψ2(i*)cos(2Nθ)+ψ3(i*)cos(4Nθ)

(4)

式中：N代表电机的转子极数；ψk(i*)是电流为i*时傅里叶级数的系数。由4条磁链曲线可以列出4个方程：

(5)

傅里叶级数的系数可以由下式算出：

(6)

系数算出后便可由式(4)求得电流为i*时任意位置对应的磁链。电流从0以一定步长遍历到测量上限值，再通过插值的方法即可得到电机的完整磁链特性。

转矩T可通过磁共能W对位置角θ的偏导数计算得出：

(7)

由式(7)即通过磁链特性得到转矩特性。

1.2.2 实现

通过给不同相通电，三相12/8 SRM一相转子可以稳定在4个位置，分别对应0°，7.5°，15°，22.5°(以不对齐位置为0°)。因此，为实现上述的方法，以测量C相为例，需执行如图2所示的步骤。

图2中，J表示为了使C相处于不同位置所需通电的相。当J为C时，转子会旋转至对齐位置，即22.5°位置；当J为BC时，根据各相对称性，转子会转至B相对齐位置与C相对齐位置的中点处，相当于C相的15°位置；当J为B时，B相会最终处于对齐位置，相当于C相的7.5°；当J为AB时，转子最终转至0°位置。值得注意的是测量时施加电压激励的对象K。文献[8]中，对电机三相同时通电以施加激励，但三相同时通电互感较大，产生较大误差。为使转子位置保持稳定，同时各相之间的互感尽可能小，因此K的实际设定如图2中所示。

图2 测量流程图(以C相为例)

按照上述步骤测得4个位置的电压电流曲线后，根据文中介绍的原理可算出转矩特性。将转矩特性转换为二维查找表的形式(横纵坐标分别对应电流，位置角，表格内为转矩值)存储于微控制器中，即完成了转矩特性表的获取。

1.3 转矩的在线估算

电机运转过程中模数转换器(以下简称ADC)每采集一组相电流和位置角，控制器便根据转矩特性表使用插值法计算得到对应的瞬时转矩值。这里插值算法选择了双线性插值法，其相较于最临近插值法拥有更高的精确度，在微控制器中的运算速度相比其它高次插值算法大幅提高。将插值得到的某时刻三相转矩值相加即得到该时刻电机的合成转矩，用微控制器中的数模转换器(以下简称DAC)输出即可通过示波器实时观测转矩波形。

2 实验验证

为了验证上面的方案，搭建了实验平台。硬件部分包括SRM，微控制器，电流电压检测电路，位置传感器，功率变换器，负载，直流稳压源等。其中所采用的电机为三相12/8 SRM。控制器采用的是STM32F103R，其内嵌了适用于电机控制的定时器和ADC。电流电压检测电路中分别使用霍尔电流和霍尔电压传感器，可以将电流和电压转化到ADC的检测范围之内。功率变换器采用的是不对称半桥结构。负载为磁粉制动器。

依照文中的步骤进行实验，得到的4条磁链曲线如图3所示。

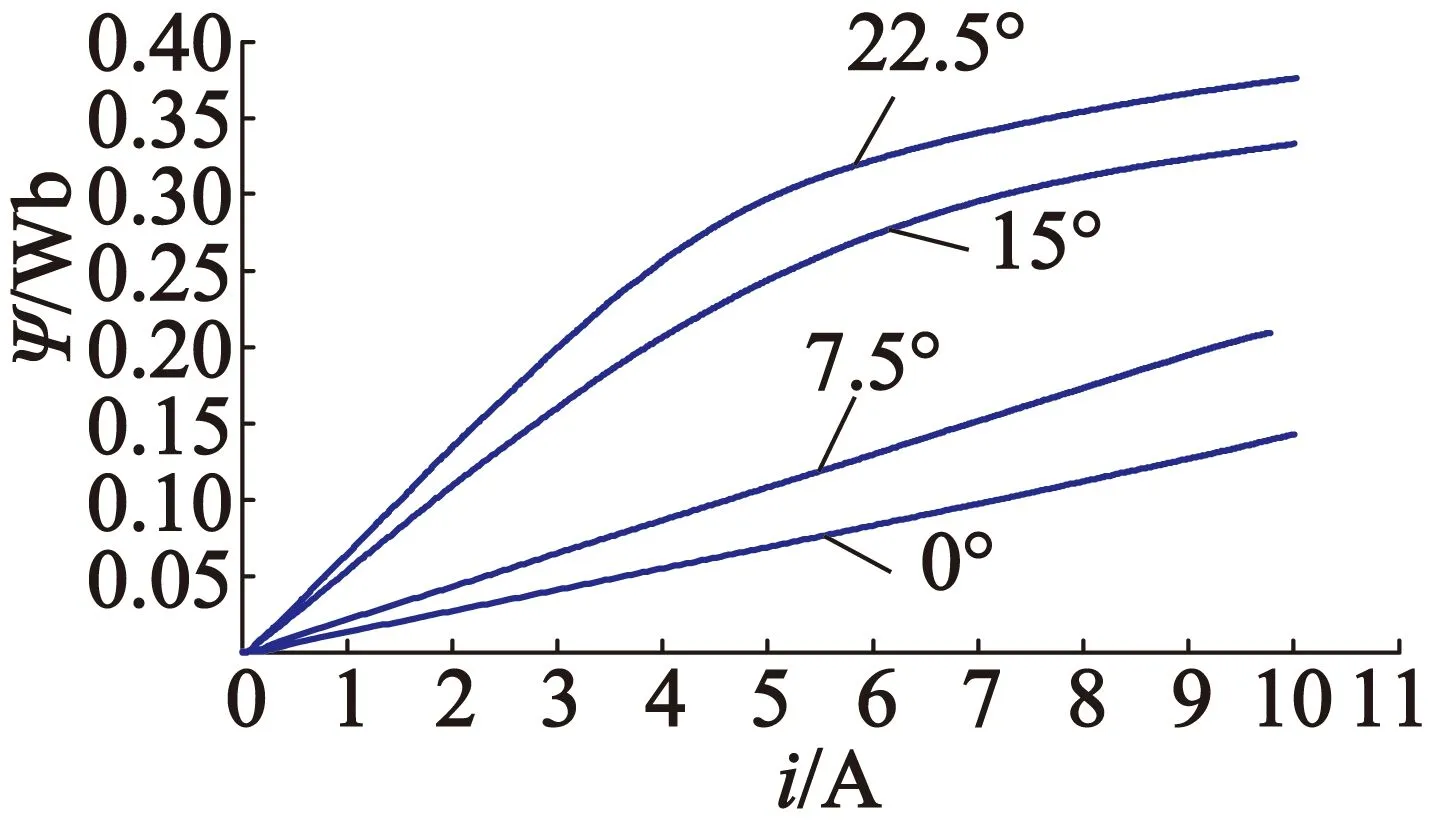
图3 4个关键位置的磁链特性曲线图

四阶傅里叶级数表示的完整磁链特性曲线图如图4所示，其中每条曲线代表某个位置下磁链与电流的关系，图中只列出了部分位置下的曲线。

图4 完整磁链特性曲线图

转矩特性如图5所示，图中只列出了部分电流值对应的转矩与位置角的关系。

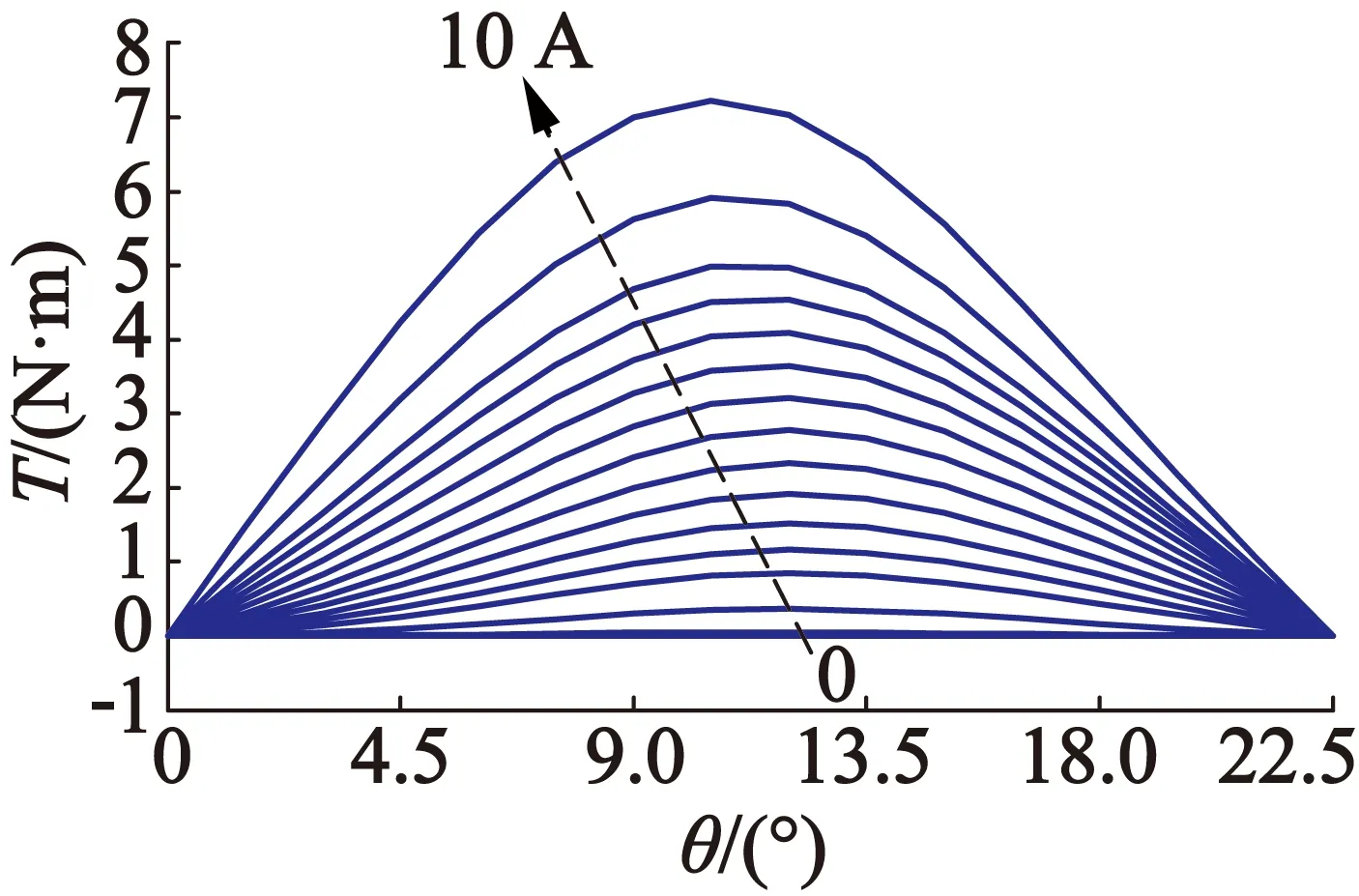
图5 转矩特性图

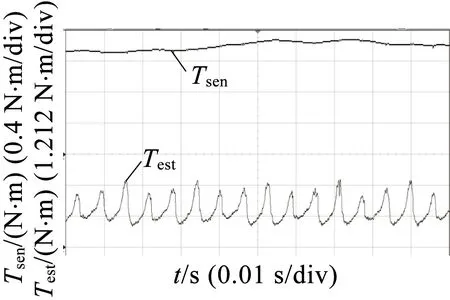
为了将在线估算结果Test和扭矩传感器的测量结果Tsen进行对比，进行了多组实验。图6的控制方式为电流斩波控制，转速400 r/min。图7为角度位置控制，转速800 r/min。图6、图7分别为不同负载下(从图6(a)到图6(d)负载递增)下的测量结果。

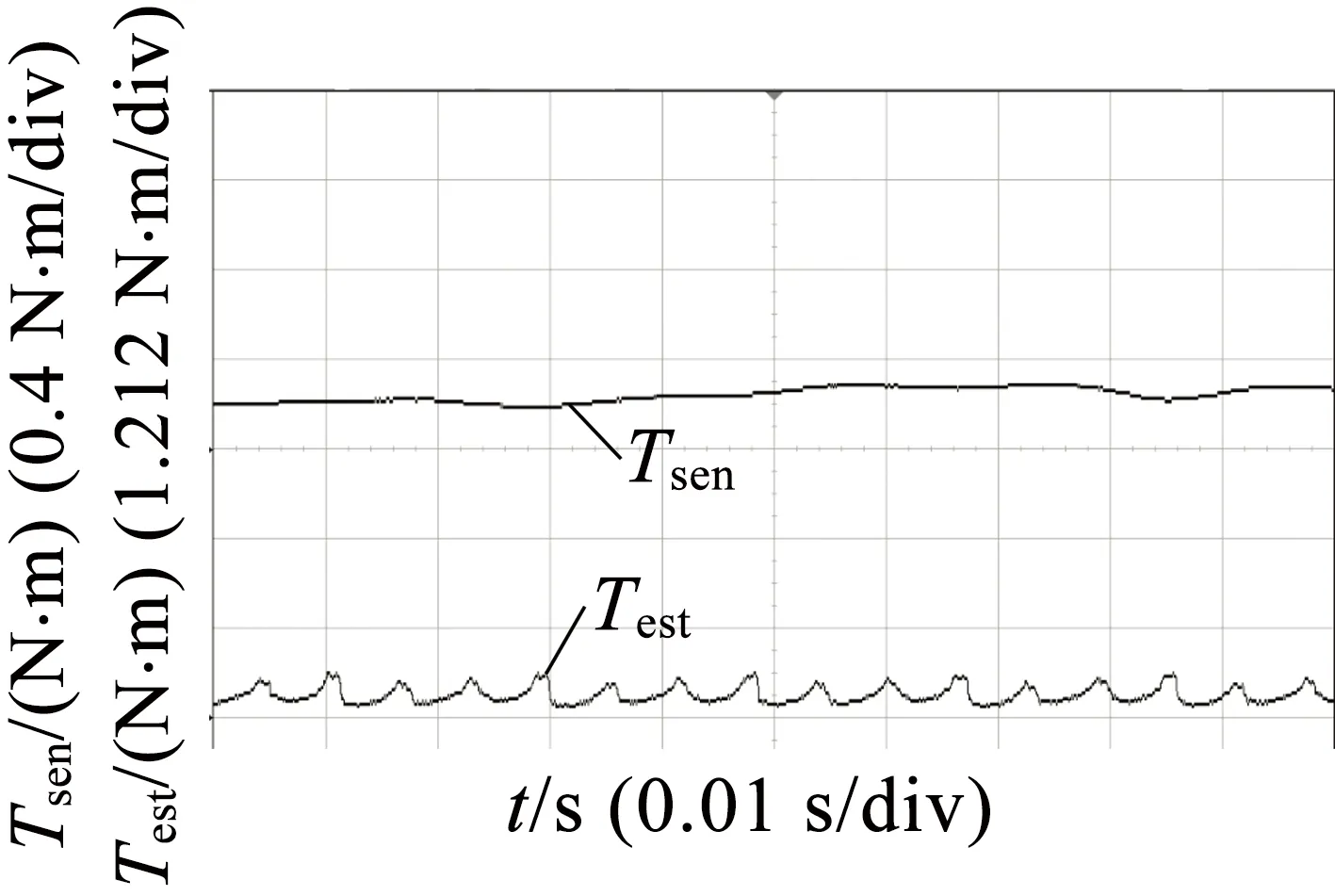
(a)

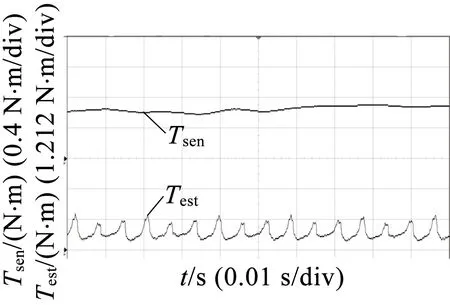
(b)

(c)

(d)

图6采用电流斩波控制，转速400 r/min时，不同负载下的测量结果

(a)

(b)

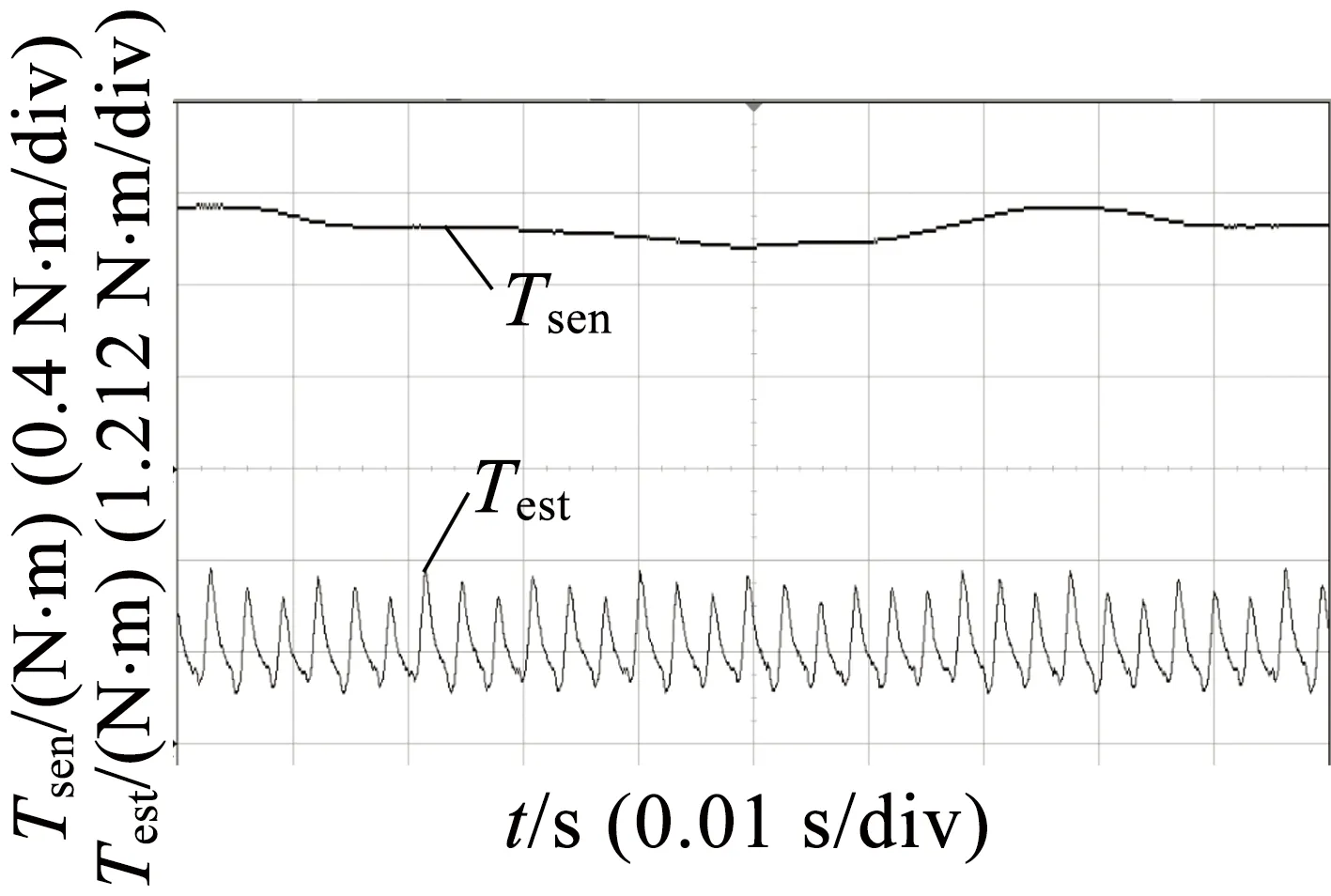
(c)

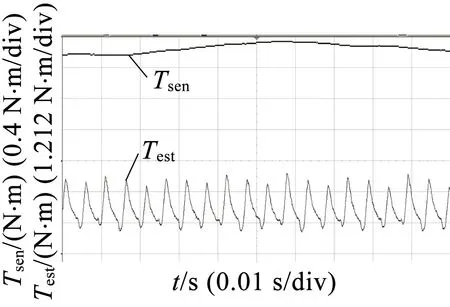
(d)

图7采用角度位置控制，转速800 r/min时，不同负载下的测量结果

根据图6和图7，可得到对比结果如表1和表2所示。

表1 电流斩波控制,转速400 r/min时，4组测量数据对比

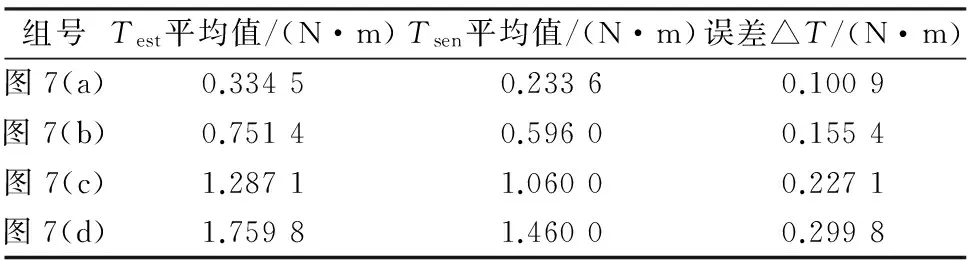
表2 角度位置控制,转速800 r/min时，4组测量数据对比

从对比结果可以看出，转矩估算的结果与扭矩传感器的测量结果数值上基本吻合，验证了方案的可行性。观察误差一栏可以发现，在角度位置控制下，高速运行时误差相对较大，并且随着负载的增大而增大。这可以从电机损耗的角度解释，该方法估算得到的转矩，由于未考虑损耗问题，可以视为输入功率Pin对应的转矩，而扭矩传感器测得的转矩则可视为电机轴上的功率Pshaft对应的转矩。图8为SRM损耗示意图。由图8可知，从输入功率Pin到最终电机轴上的输出功率Pshaft，共有铁损、铜损、机械损耗和杂散损耗4种损耗。其中，铜损与电流有效值的平方成正比。铁损除了与电机铁心材料有关外，还与电机铁心的磁场有密切关系。机械损耗一般由轴承摩擦损耗和通风损耗组成，主要与转速、加工精度、润滑脂及温度、电机结构等有关。杂散损耗原因很复杂，一般可以按铜损、铁损、机械损耗三者之和的7%计算[9]。综上，可以得出电机在高速运转时，铜损、机械损耗、杂散损耗相对低速运转时会明显增大，所以表2中误差明显大于表1。在转速一定时，随着负载的增大，铜损会随着电流的增大而增大，因此表2中4组误差递增。而表1中由于误差本身较小，因此4组误差递增关系不明显。

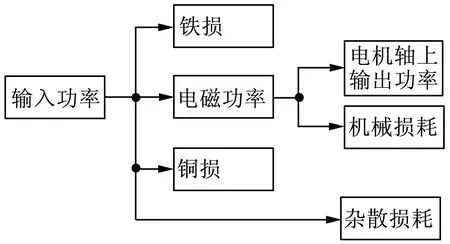
图8 SRM损耗示意图

3 结 语

本文介绍了一种SRM瞬时转矩在线估算方法，它采用一种简单快速的方法获取电机转矩特性，无需位置传感器和转子夹紧装置。之后，通过测量相电流和转子位置角，使用双线性插值计算，得到瞬时转矩。该方案的可行性得到了实验验证。实验所用样机为三相12/8 SRM，该方法在其它结构SRM上亦可使用。

[1] 吴红星，孙青杰，黄玉平，等.开关磁阻电机非线性建模方法综述[J].微电机，2014，47(5):83-92.

[2] 张剑.开关磁阻电机转矩测试系统实验平台建立[D].邯郸：河北工程大学，2015.

[3] 李大鹏，代尚芳.基于BP神经网络的开关磁阻电机转矩观测器[J].伺服控制，2012(1):38-40.

[4] 郑洪涛，李玉榕，乔斌，等.基于模糊神经网络开关磁阻电动机转矩观测[J].仪器仪表学报，2002，23(4):351-360.

[5] 孙建忠，张凯，王诗琦，等.基于Labview的开关磁阻电机瞬态转矩测试系统研究[J].大连理工大学学报，2013，53(3):443-446.

[6] CHEN H J,JING W P.Flux linkage determination of the switched reluctance motor from measurable quantities at steady-state operations[J].IET Electric Power Applications,2011,5(2):210-216.

[7] SALMASI F R,FAHIMI B.Modeling switched-reluctance machines by decomposition of double magnetic saliencies[J].IEEE Transactions on Magnetics,2004,40(3):1556-1561.

[8] SHEN L,WU J H,YANG S Y,et al.Fast flux linkage measurement for switched reluctance motors excluding rotor clamping devices and position sensors[J].IEEE Transactions on Instrumentation and Measurement,2013,62(1):185-191.

[9] 杨丽.开关磁阻电机的损耗及热分析研究[D].南京：南京航空航天大学，2006.