降低转矩脉动的六相感应电机直接转矩控制
2018-04-26姚月琴王秀琳
姚月琴,王秀琳
(1.盐城工业职业技术学院,盐城 224005;2.盐城工学院,盐城 224001)
0 引 言
多相电机自19世纪60年代提出以后,由于具有许多优于三相电机的优点,例如:更好的容错特性,更低的逆变器桥臂电流和更高的功率密度等,在电力传动领域得到了广泛应用[1-3]。其中,多相电机中的典型代表为非对称六相感应电机(以下简称ASIM),因为其容易通过定子绕组重复绕制实现[3-4],但多相电机的驱动系统存在低次电流谐波的问题,进而产生低次转矩脉动[5-6]。对于n相电机,通常最低次转矩脉动为2n±1次,而对于ASIM,由于2套三相绕组相移30°,产生转矩脉动的电流谐波次数为12n±1(n=0,1,2,…)[7-8],而6n±1(n=1,3,5,…)次谐波不产生转矩脉动,但是将产生损耗,降低效率。
直接转矩控制(以下简称DTC)相对矢量控制具有结构简单、转矩响应快、鲁棒性好的优点[9-11],将DTC控制应用于ASIM带来的主要问题就是电流谐波产生转矩脉动的问题。文献[12]提出了一种无差拍DTC技术,通过设置恒定的开关频率来减少电流谐波并提高驱动性能。文献[13]开发了一种改进型查找表方案的DTC技术,用于ASIM以期减少电流谐波,其中电压矢量的选择取决于辅助x-y子空间中磁链的位置。文献[14]将合成虚拟电压矢量的概念引入到了对称六相永磁同步电机控制中,这可以避免对辅助x-y子空间中定子磁链位置进行估计。
本文在前述研究基础上,将合成虚拟电压矢量的概念引入到ASIM控制中,即在传统DTC方案中引入了2个虚拟电压矢量,从而避免了前述文献中需要对开关序列的重新设计,以及特殊查找表的使用,降低了计算量。最后通过试验验证了新型控制策略的有效性。
1 ASIM驱动系统数学模型
1.1 ASIM数学模型
ASIM具有2套三相定子绕组,它们在空间上移相30°电角度。可采用文献[7]中开发的解耦技术对ASIM进行建模,将六维系统转换为3个相互正交的二维子空间d-q,x-y和o1-o2的集合。具体的转换矩阵T的表达式如下[8]:
(1)
式(1)中的变换矩阵T将基波分量和12n±1(n=0,1,2,…)次谐波分量映射到了d-q子空间中,同时将6n±1(n=1,3,5,…)次谐波分量和3n(n=1,3,5,…)次谐波分量分别映射到了x-y子空间和o1o2子空间中。然而,只有d-q子空间的电流谐波将影响到转矩。将式(1)应用到电机的定转子电压和磁链方程中,可以得到:
(2)
(3)
(4)
Te=3p(ψdsiqs-ψqsids)
(5)
式中:vds,vqs和vxs,vys为d-q子空间和x-y子空间对应电压;ψds,ψqs和ψxs,ψys为d-q子空间和x-y子空间对应磁链;ids,iqs和ixs,iys为d-q子空间和x-y子空间对应电流;Rs和Rr为定转子电阻;Ls,Lr,Lls,Llr和Lm为定转子自感、定转子漏感和互感;ωr为转子角速度;Te为电磁转矩;p为电机极对数。从图1的ASIM驱动系统电路中可看出,由于具有2个互相隔离的中性点,故可以忽略零序分量,即可以将o1o2子空间中的方程省略。
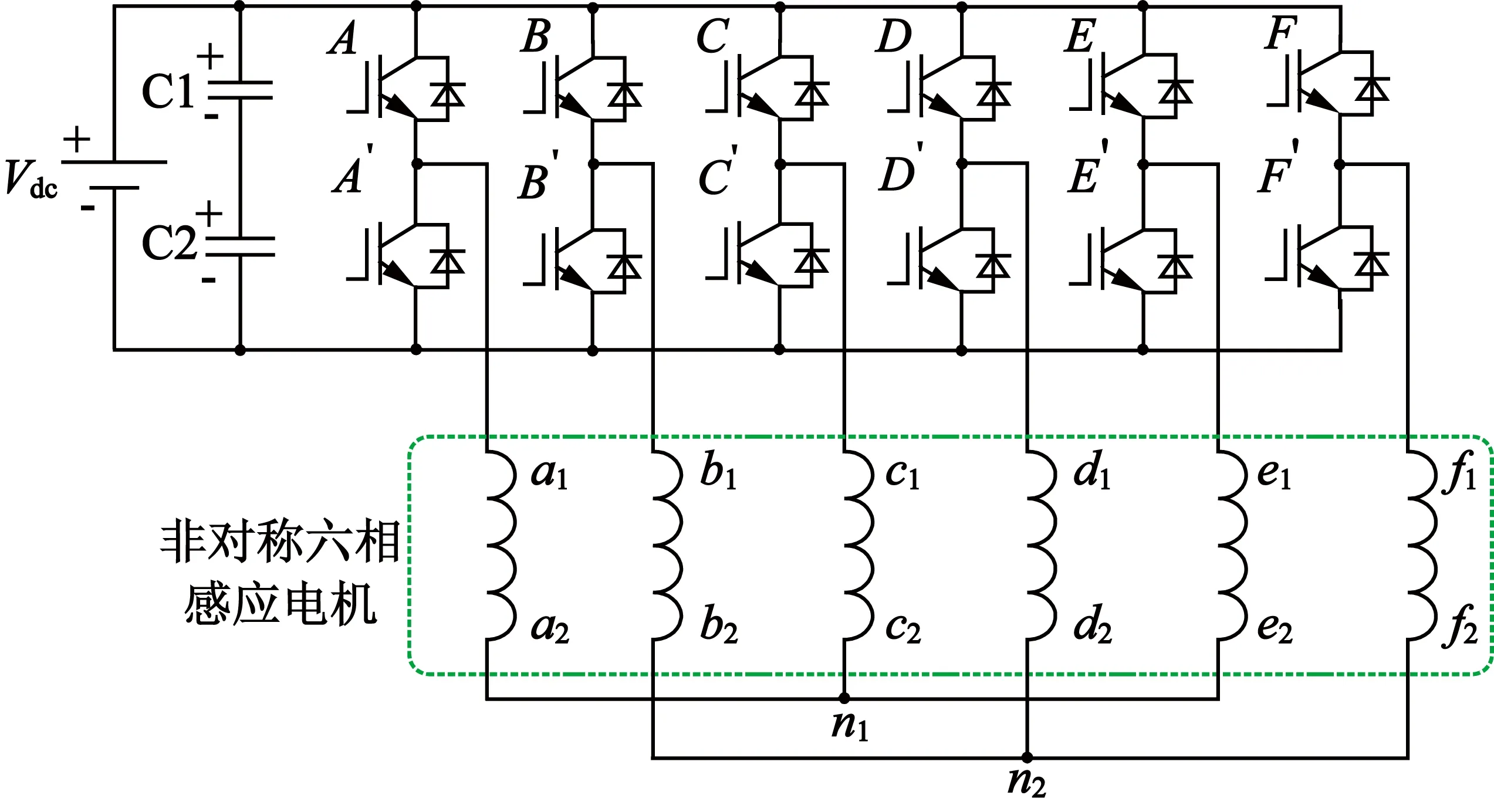
图1 ASIM驱动系统电路
1.2 两电平六相逆变器数学模型
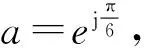
(6)
所有64个矢量可分为两类:60个有效矢量和4个零矢量。而在60个有效矢量中,有12个是冗余的,故有48个是真正有效矢量。图2为全部矢量在d-q和x-y子空间中的构成图,有效矢量合成L1,L2,L3和L4四种不同的幅值,将有效矢量分为4组,L1组矢量幅值最大,L4组矢量幅值最小。

(a) d-q子空间中的电压矢量
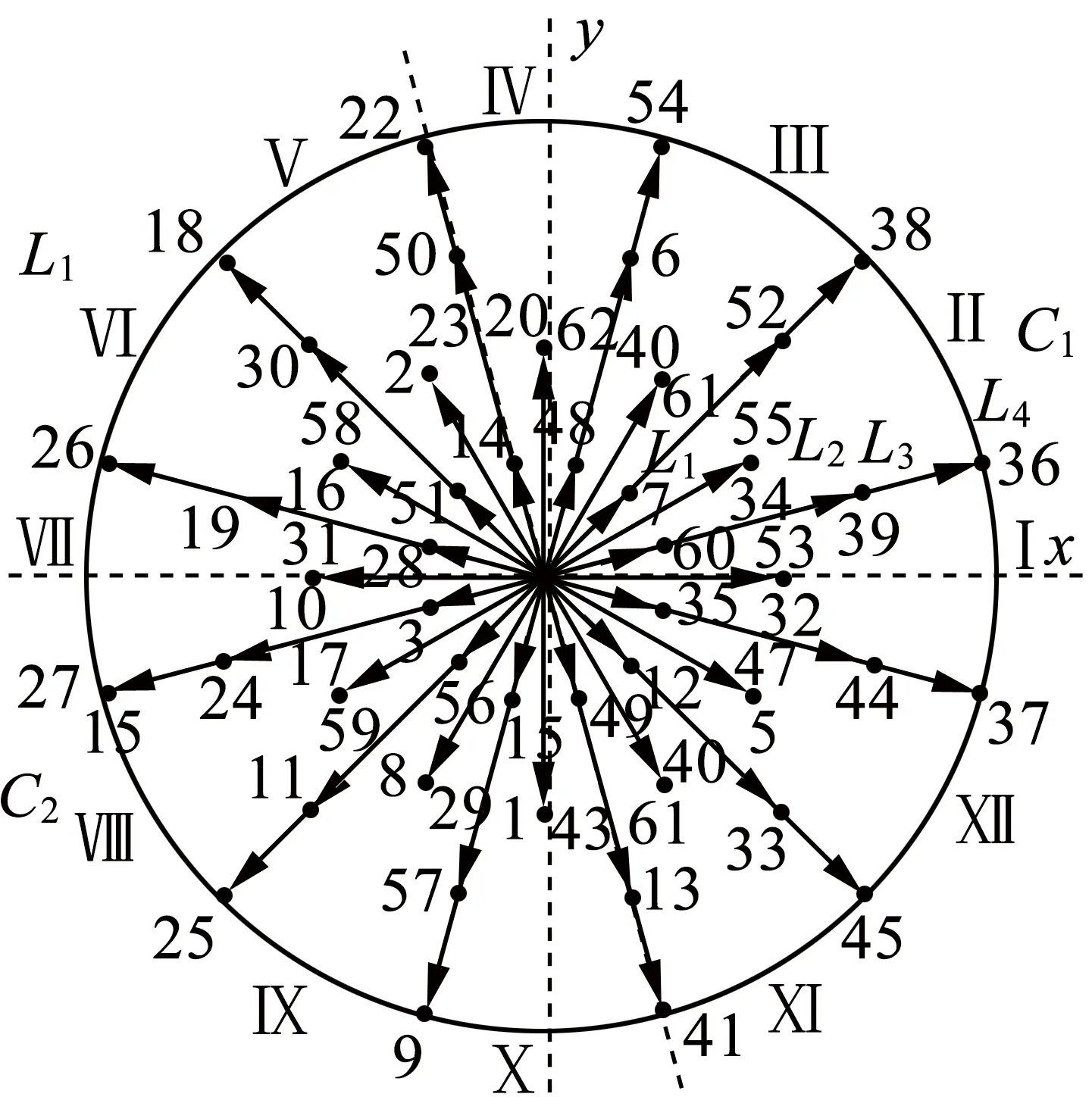
(b) x-y子空间中的电压矢量
图2d-q和x-y子空间中的电压矢量
2 传统的DTC控制策略
将三相感应电机传统DTC控制系统中的查找表进行简单扩展后,即可得到ASIM的传统DTC控制策略,具体如图3所示。随着可用矢量的增加,d-q子空间被分为12个扇区,如图4所示。为了方便起见,将传统DTC控制命名为DTC1,DTC1仅使用L1组的电压矢量,并且不考虑电压矢量对x-y子空间电流谐波的影响,从而导致较大的转矩脉动。

图3 传统的DTC方案框图
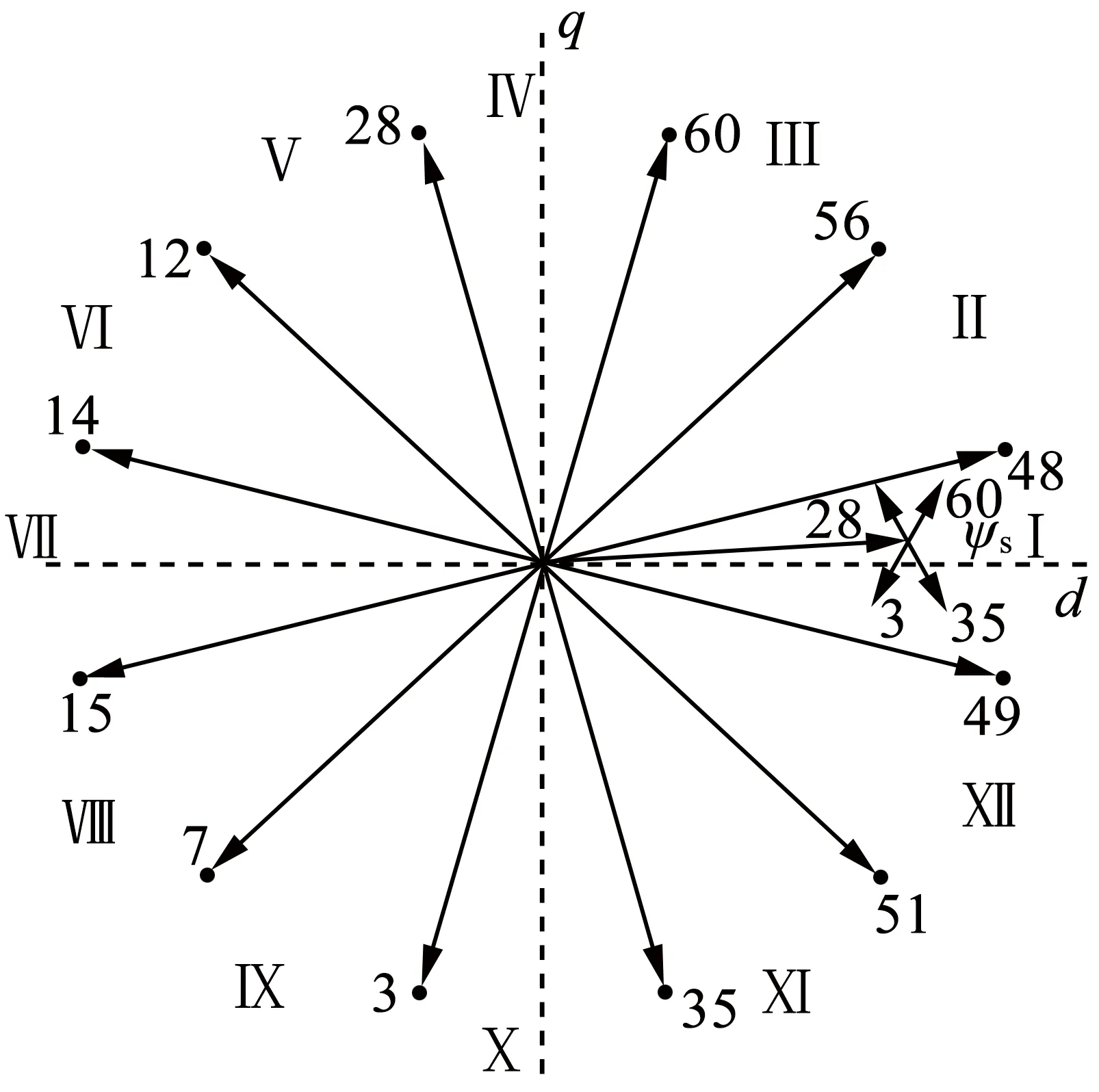
图4 传统的DTC下电压矢量选择
图3中,逆变器的开关状态和直流母线电压Vdc决定了输出相电压。通过使用式(1)中的变换,可得到d-q子空间中的电压和电流。然后,基于式(2)中的电压模型,可估计d-q子空间中的定子磁链,基于式(5)可估计出转矩。定子磁链幅值由2级比较器控制,转矩由3级比较器控制。图4中,假设定子磁链ψs位于扇区Ⅰ,增大转矩的矢量选择为V60和V28,减小转矩的矢量选择为V3和V35,则通过应用零矢量可将转矩保持。类似地,选择矢量V60和V35导致磁链幅度的增加,选择矢量V3和V28将使得磁链幅值的降低。表1为对应DTC1的开关表。
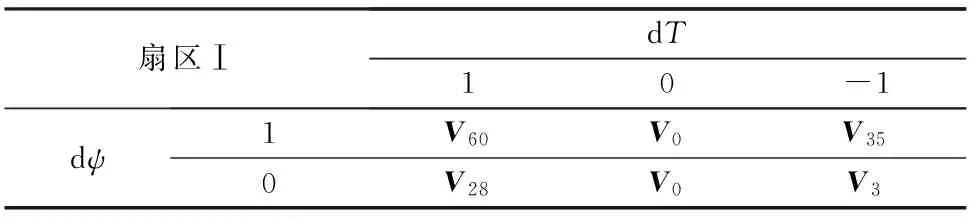
表1 DTC1控制时的开关查找表
3 改进型DTC控制策略
以减少x-y子空间中电流谐波为出发点,文献[7]给出另一种改进型的DTC控制,命名为DTC2。DTC2的控制框图如图5所示。由图5可见,DTC2使用了2个不同的开关查找表,第1个开关查找表和表1一致,第2个开关查找表如表2右侧所示。
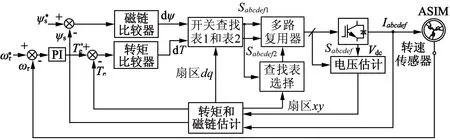
图5 改进型DTC方案框图

第1个开关查找表第2个开关查找表扇区ⅠdT10-1扇区ⅠdT10-1dψ1V60V0V350V28V0V3dψ1V24V0V190V44V0V39
当磁链位于扇区Ⅰ中时,若磁链和转矩都要增加,则从第1个表中选择电压矢量V60,从第2个表中选择电压矢量V24,在d-q子空间中,V60和V24位置相同,因而是同相的,对磁链和转矩的影响是类似的。然而图2(b)中,在x-y子空间中,V60和V24位置是相反的,且分属于C1半圆区和C2半圆区。故可通过式(4)中最后2个方程来估计磁链是位于x-y子空间中C1半圆区中还是C2半圆区,前者选择电压矢量V24,后者选择电压矢量V60,在这2种情况下,由于选择施加来自相反方向的矢量,所以x-y子空间中的合成磁链将减小,具体选择原理如表3所示。表3中“1”代表选择第1个开关查找表,而“2”代表选择第2个开关查找表。2个开关查找表的输出给到1个多路复用器,多路复用器的输出由表3决定。

表3 DTC2控制时的开关查找表
4 新型DTC控制策略
前述DTC2控制中通过合理选择合成矢量降低了x-y子空间中电流谐波的影响,使用的是L1组和L2组的矢量。下面将设计新型DTC控制,命名为DTC3,不同于DTC2又增加了L4组的运算。
图1中,V60,V24和V36这3个矢量在d-q子空间中是同相的,故3者对磁链和转矩的影响近似,而在x-y子空间中,V24的相位和其余2个是相反的。因此,针对V24和V36之间的选择类似于DTC2算法。假设选择了V36和V24,那么,根据磁链在x-y子空间中位于C1半圆区中还是C2半圆区来最终决定选择应用哪个矢量。同理,V60和V24的选择也一样。设V36和V24构成了虚拟矢量VS3,V36和V24构成了虚拟矢量VL3,VS3和VL3概率均为50%,VS3和VL3的幅值分别:
(7)
虚拟矢量集VSx(x=1,2,…,12)代表了来自L2组和L4组矢量的组合。虚拟矢量集VLx(x=1,2,…,12),代表了来自L1组和L2组矢量的组合。图6为d-q子空间中所有虚拟矢量集合,一共包含24个虚拟矢量,使用时遵循减少x-y子空间分量为原则。
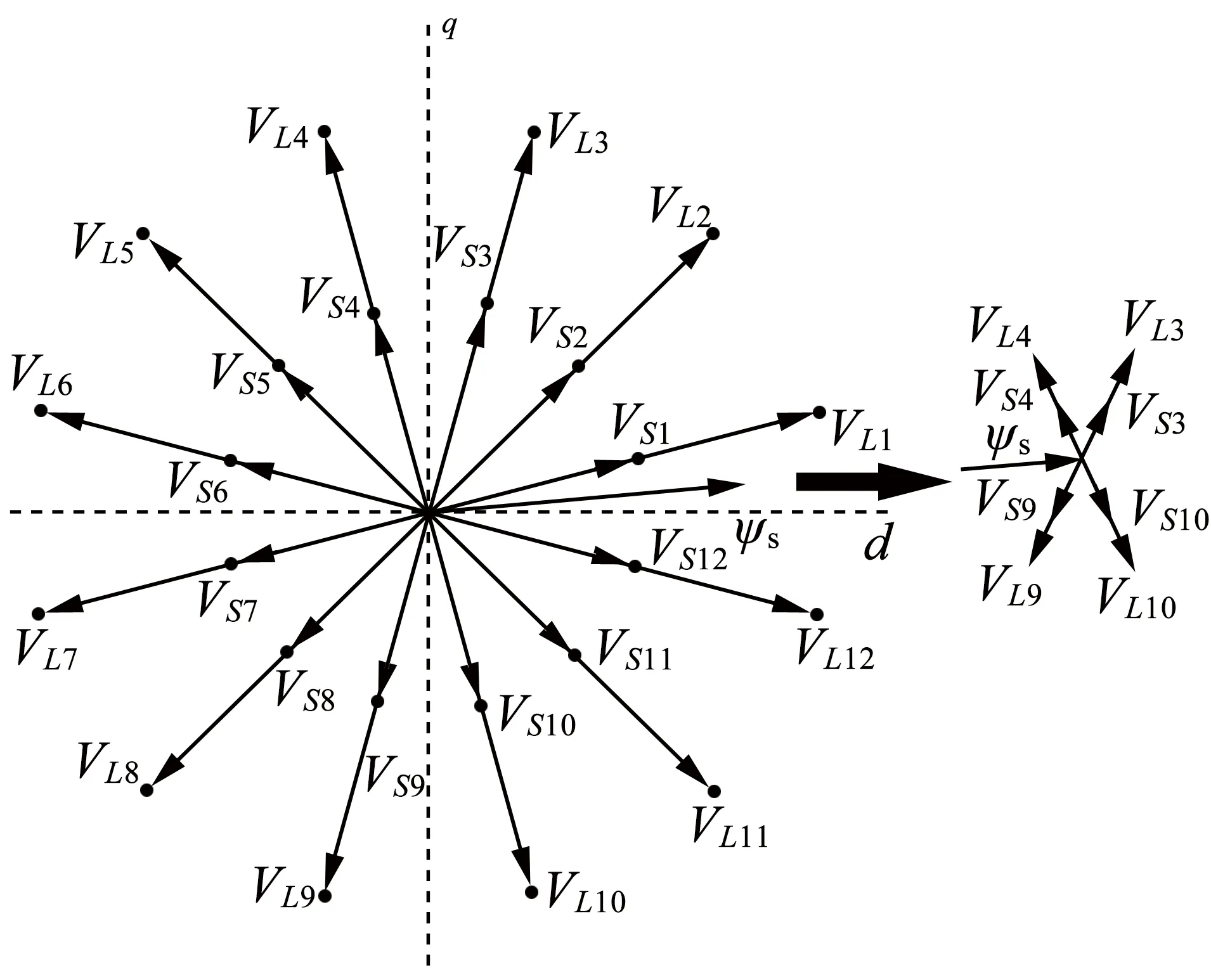
图6 d-q子空间中的虚拟电压矢量
类似于文献[15]给出的三相感应电机转矩变化率的推导方法,可推导出实施有效矢量和零矢量到ASIM的转矩变化率方程如下:
(8)

从式(8)可以看出,施加有效矢量后的转矩变化率取决于电压矢量幅值和电机转速的大小,而零矢量的施加总是倾向于减小转矩,减小的程度取决于电机转速,即低转速时减小慢,高转速时减小快。对于虚拟电压矢量VSx,低转速对应正的转矩变化率;高转速对应负的转矩变化率,而虚拟电压矢量VLx施加后总是正的转矩变化率,且转速越低,变化率越大。在较低转速时,VLx引起的转矩上升率大于VSx引起的转矩上升率,因为上升率主要取决于电压矢量的幅值。在较高转速时,和零矢量相比,VSx引起的转矩变化更为平缓。
考虑到多级转矩比较器能有效降低转矩脉动[16],故在DTC3设计中引入了5级转矩比较器,如图7所示。
图7中,当转矩误差大于阈值HB时,则给出快速增大转矩指令,即VLx;而当转矩误差高于阈值HA但小于阈值HB时,给出逐渐增加转矩指令,即VSx。转矩变化率取决于所选矢量幅值大小,故5级比较器的带宽比等于不同矢量的幅值比,具体如下:
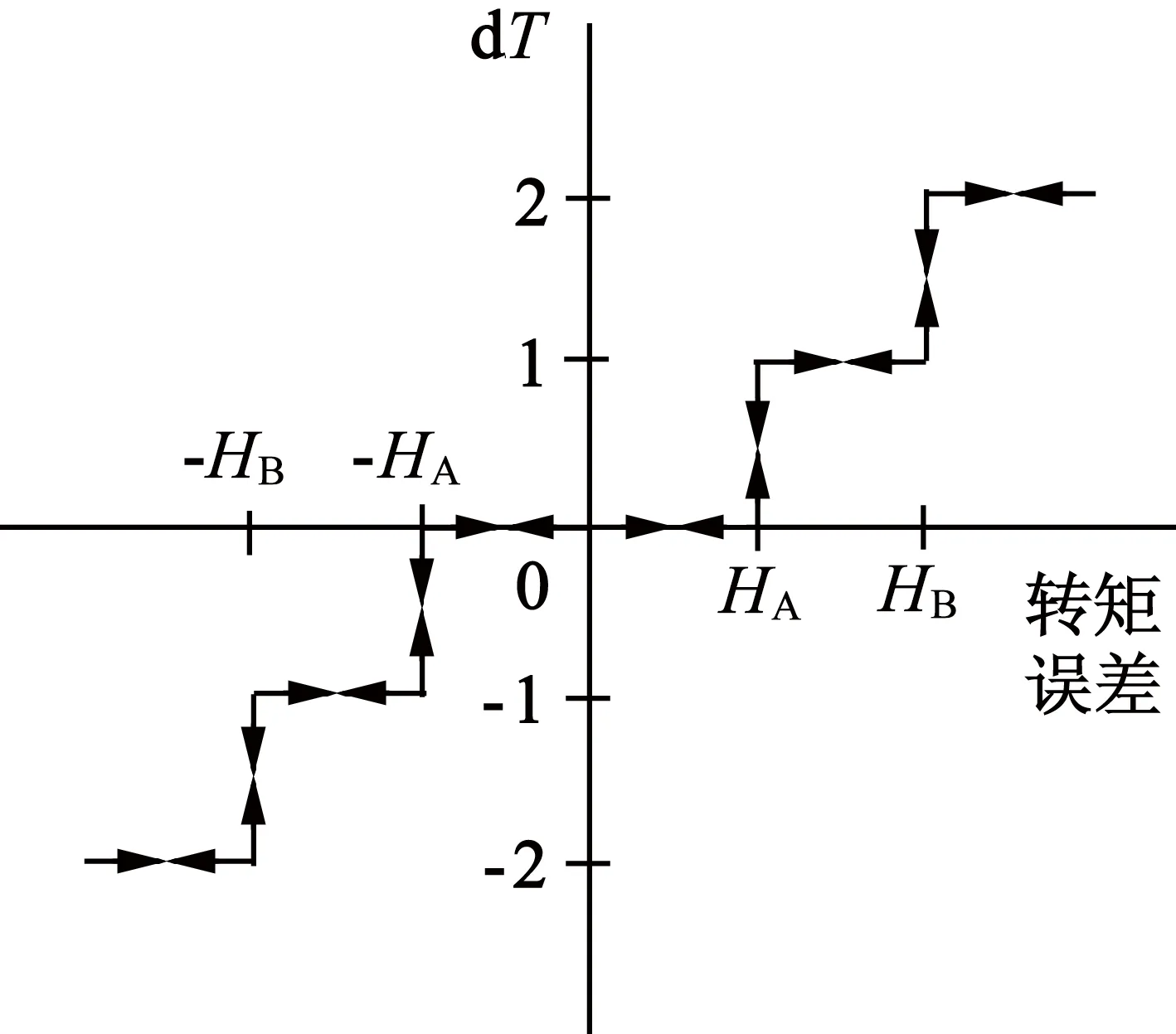
图7 五级转矩比较器
HA:HB=|VSx|∶|VLx|=0.322Vdc∶0.557 5Vdc
(9)
考虑到低转速时,有效矢量引起的转矩上升大于由零矢量引起的转矩下降;而高转速时,零矢量引起的转矩下降大于由有效矢量引起的转矩上升。因此,为了减小转矩波动,设计了如表4所示的开关查找表。在低转速稳态运行时,使用VSx和零矢量,从而转矩误差保持在阈值HA以内,而在高转速稳态运行时,使用VSx和VLx,从而转矩误差控制在阈值HA和阈值HB之间。
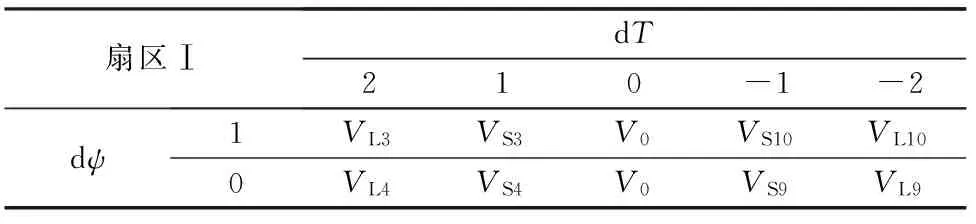
表4 DTC3控制时的开关查找表
综上所述,可以得到DTC3控制策略的控制框图和DTC2类似,如图5所示,但查找表进行了升级,并采用了5级转矩比较器。
5 实验验证
为了验证新型DTC3控制策略降低ASIM转矩脉动的实际效果,采用DTC1,DTC2和DTC3对比实验的方法进行了研究。实验系统构成如图8所示,实验用ASIM参数如表5所示。从图8中可以看出,核心算法如磁链估计和开关查找表的实现载体为DSP芯片TMS320F28377S,采样频率为10kHz,控制量采用芯片的数模转换模块输出到示波器和上位机进行观测和记录,转速由增强型正交编码器进行测量,定子电流采用LEM传感器测量,采用机械制动器模拟电机负载,逆变器采用三菱IPM模块实现,开关频率为10kHz。控制算法中设置DTC3的比较器阈值HA和HB分别为0.173N·m和0.3N·m,而DTC1和DTC2的比较器阈值设置为0.3N·m,3种控制策略的磁链比较器带宽均设置为0.003Wb。对比实验分为稳态对比实验和动态对比实验进行,以达到充分验证的目的。
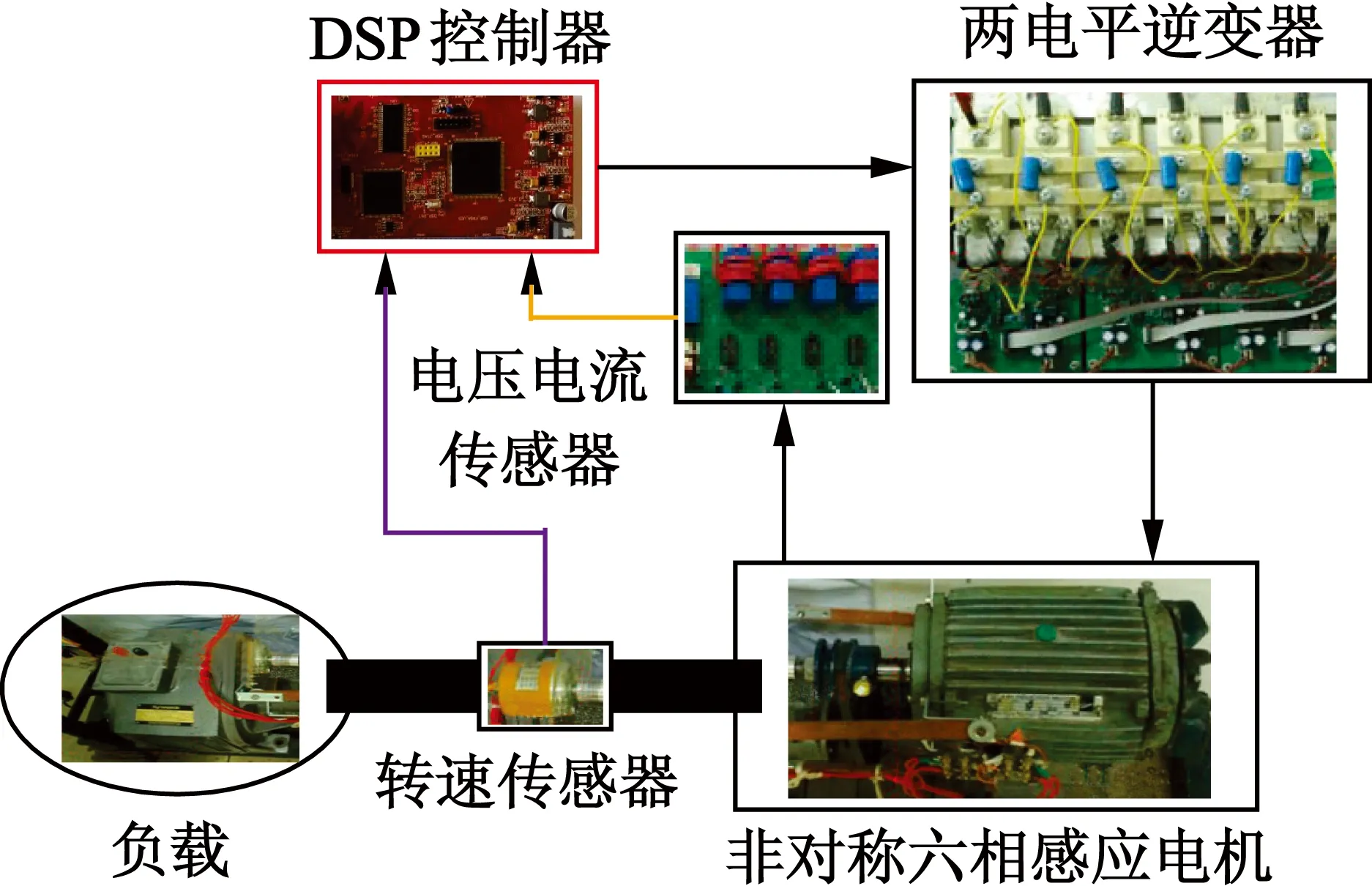
图8 实验系统

表5 实验用ASIM参数
5.1 稳态试验
图9为电机转速控制在2 500r/min,负载转矩保持2N·m时的稳态波形。其中图9(a)至图9(c)为在不同DTC控制策略下,d-q子空间和x-y子空间中的磁链轨迹波形。在DTC1,DTC2和DTC3控制方案作用下,稳态d-q子空间中磁链轨迹波形类似,但图9(a)对比图9(b),以及对比图9(c)可以看出,采用DTC2和DTC3控制后,稳态x-y子空间中磁链轨迹偏移显著减少。图9(d)至图9(f)为在不同DTC控制策略下,电机输出电磁转矩波形。DTC1和DTC2控制下波动范围分别0.27N·m和0.26N·m,而使用DTC3控制方案,电磁转矩纹波明显较DTC1和DTC2减小,波动范围只有约为0.11N·m。

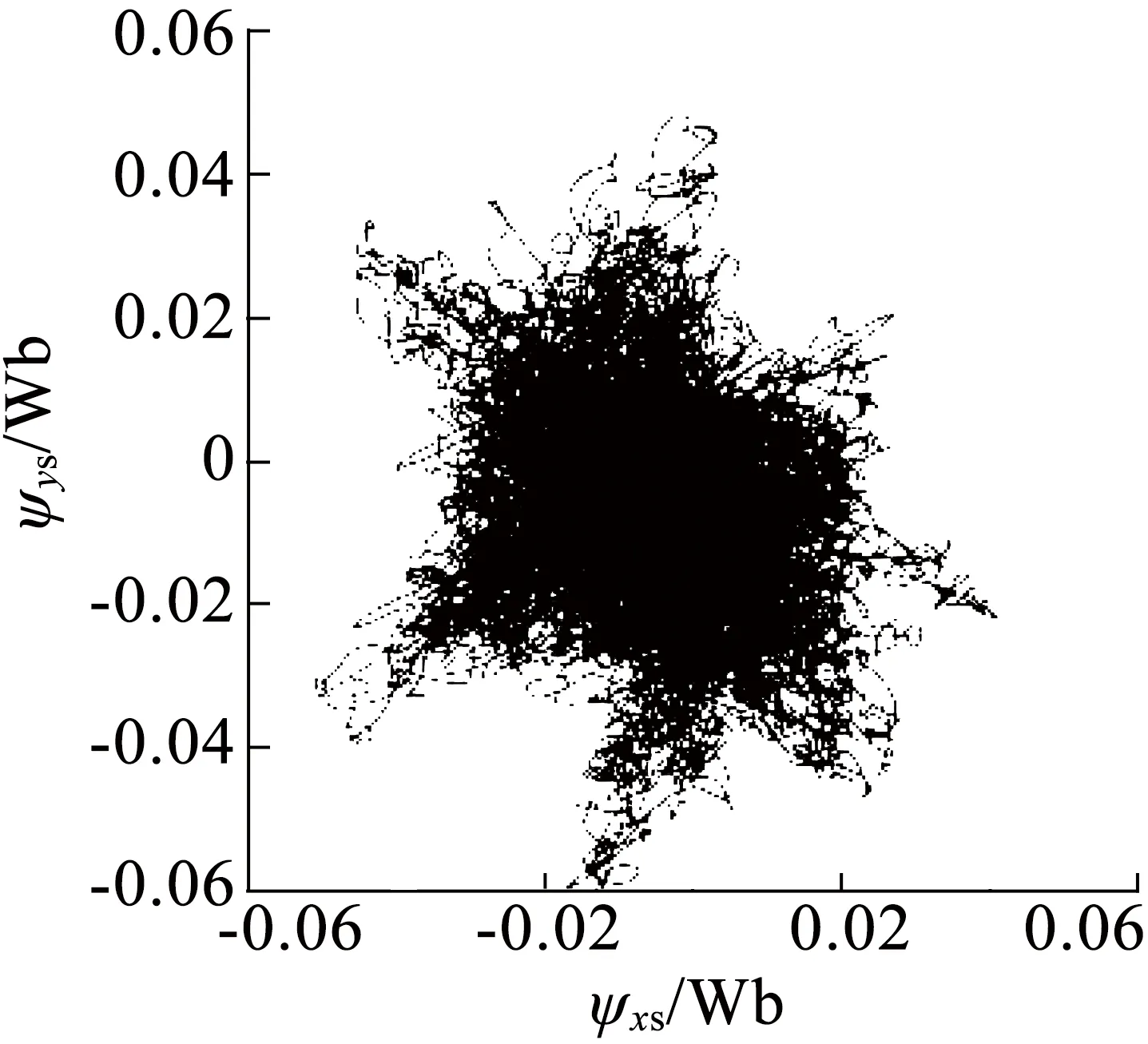
(a)DTC1控制下的磁链轨迹波形
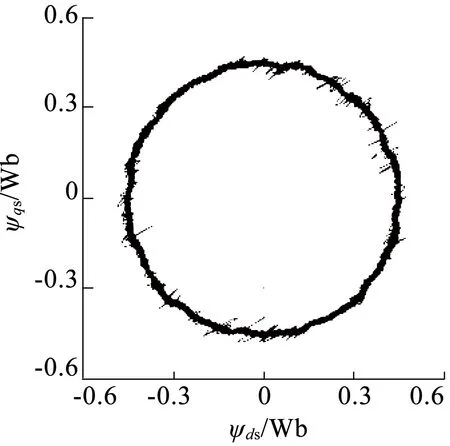

(b)DTC2控制下的磁链轨迹波形
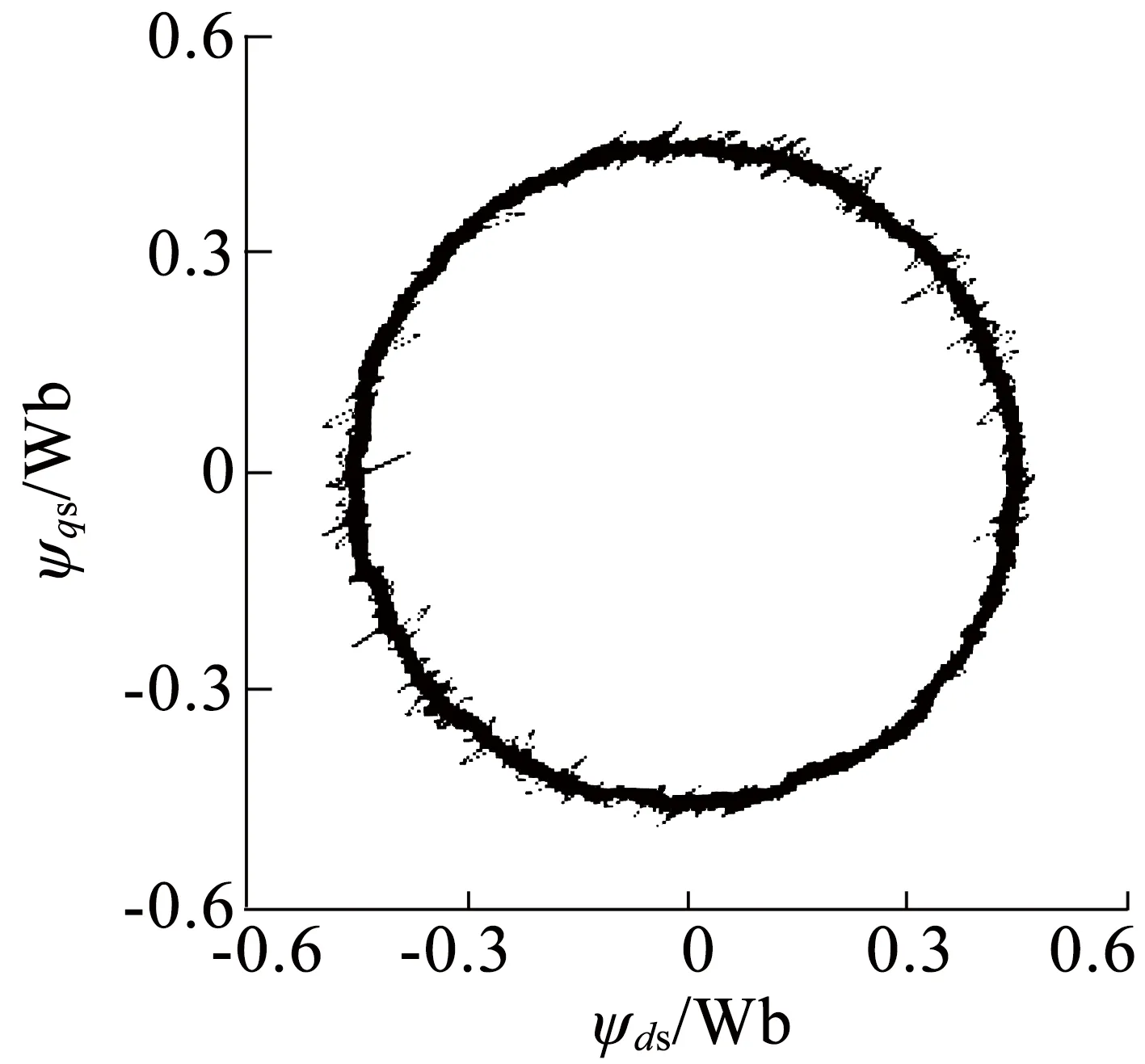
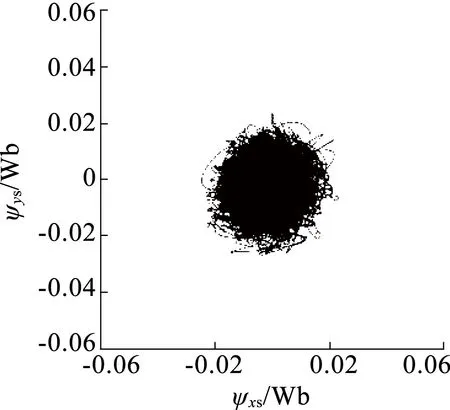
(c)DTC3控制下的磁链轨迹波形
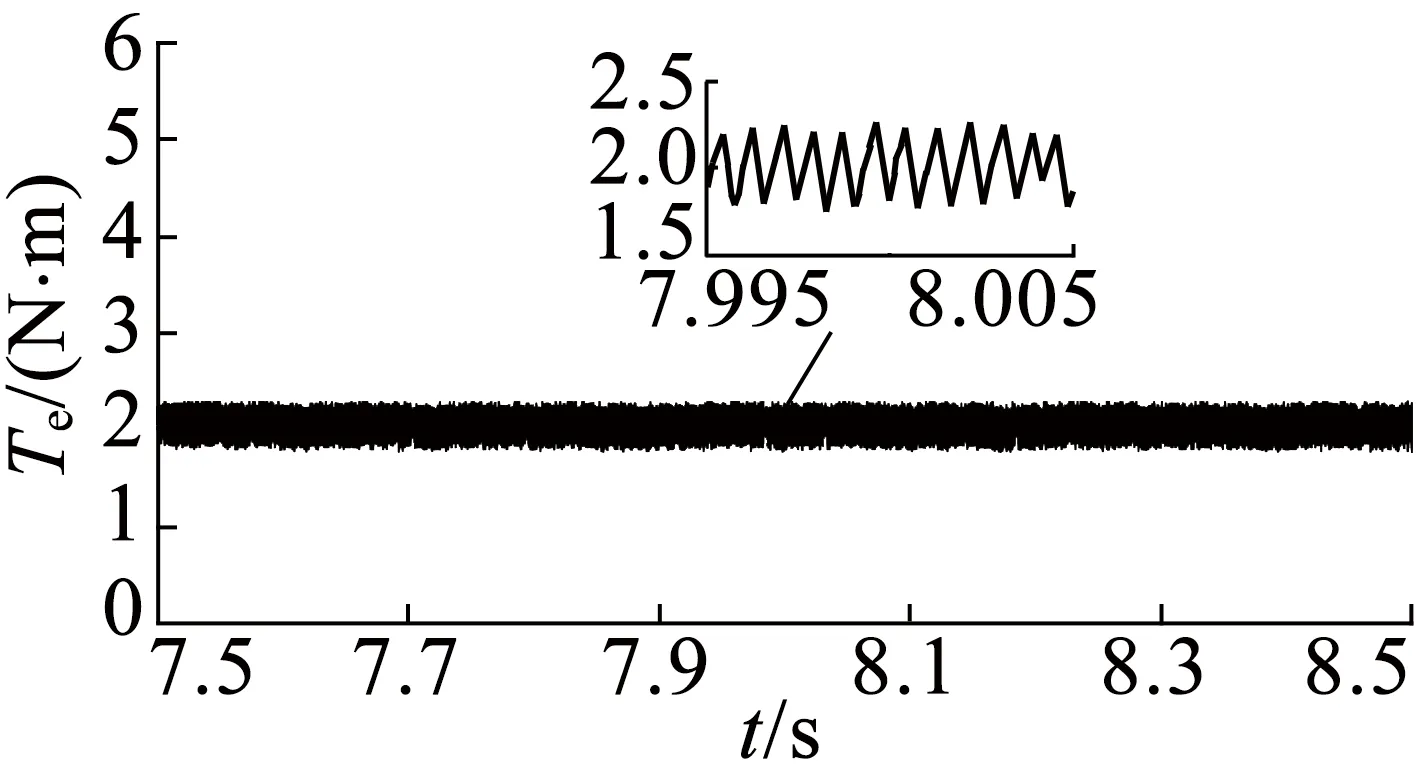
(d) DTC1控制下的输出电磁转矩波形

(e) DTC2控制下的输出电磁转矩波形
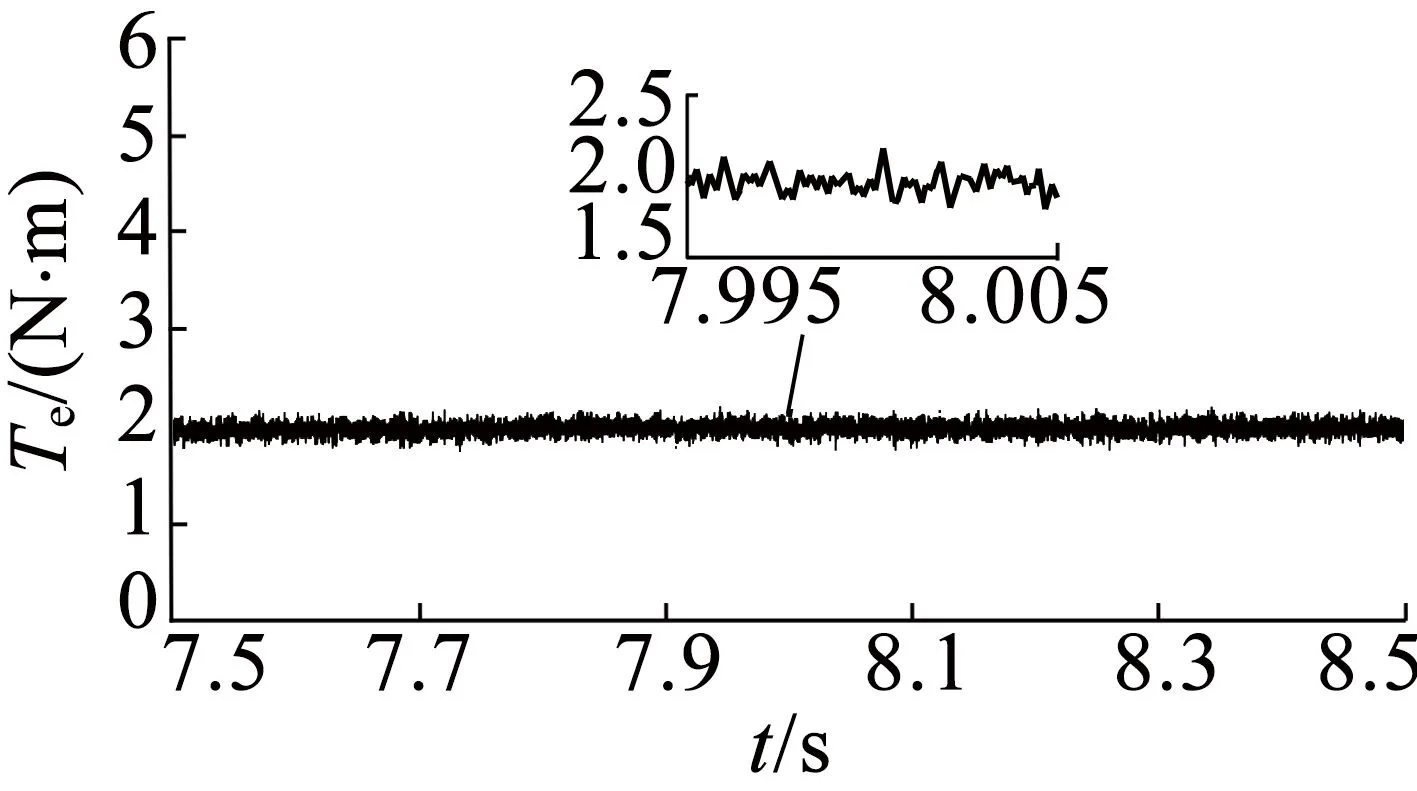
(f) DTC3控制下的输出电磁转矩波形
5.2 动态实验
图10为电机转速恒定控制在2 000r/min,负载转矩为0.3N·m,然后突加负载转矩到2N·m的实验波形。其中图10(a)至图10(c)分别为DTC1方案、DTC2方案和DTC3方案下的转矩和转速动态波形。可以推断,与DTC1和DTC2方案相比,采用DTC3方案后的动态性能没有明显变化,保持了DTC动态响应快的优点。
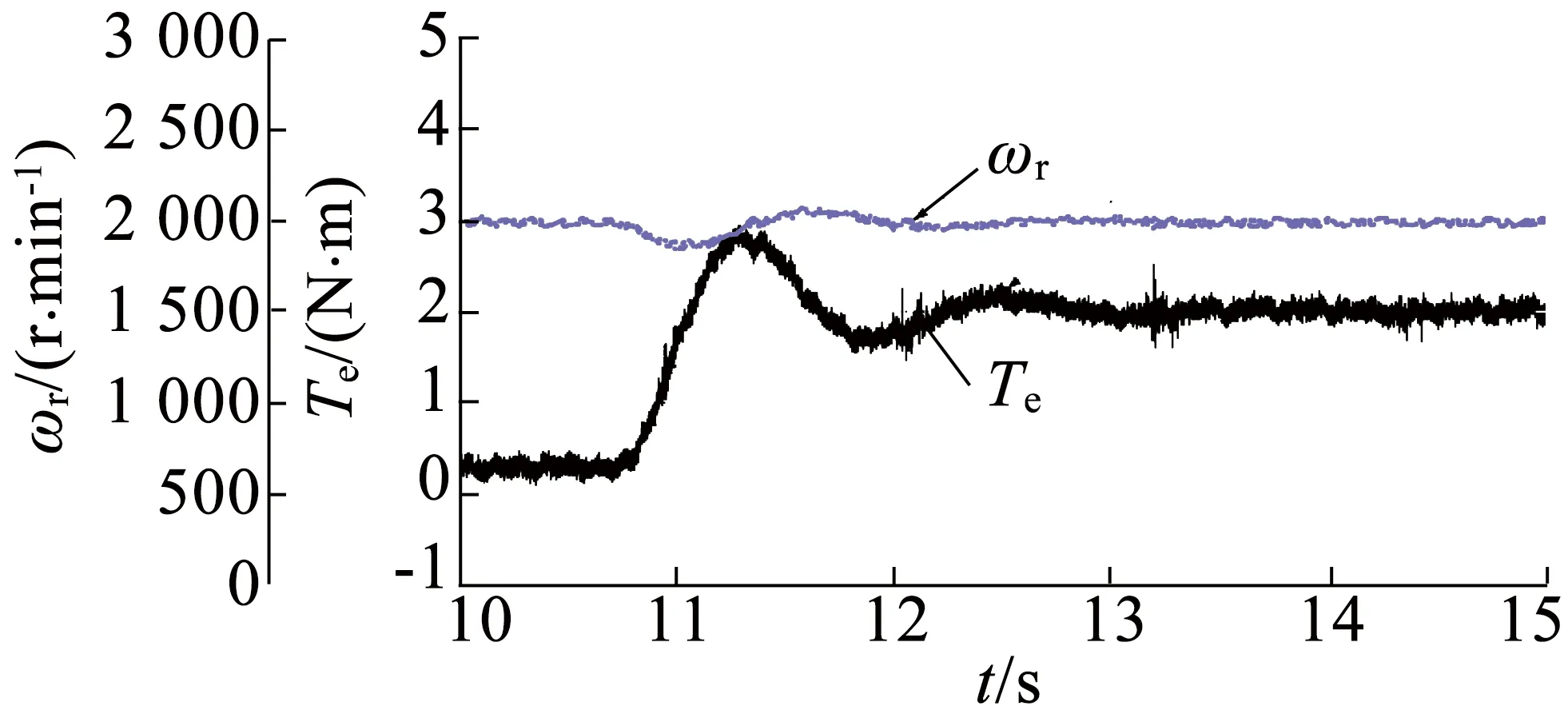
(a) DTC1控制下的转矩和转速动态波形
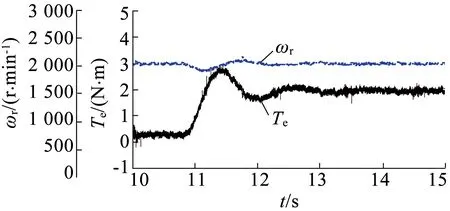
(b) DTC2控制下的转矩和转速动态波形
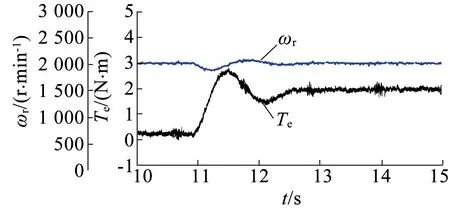
(c) DTC3控制下的转矩和转速动态波形
6 结 语
围绕传统ASIMDTC带来的转矩脉动问题,本文设计了一种新型的DTC控制方案,现总结主要结论如下:1)理论分析表明,x-y子空间中电流谐波对转矩脉动有较大的影响,而新型DTC方案通过引入大幅值矢量合成两组虚拟矢量,显著优化了x-y子空间中电流谐波;2)引入2组虚拟矢量的同时,设计了5级转矩比较器,进一步降低了实际输出转矩脉动;3)试验结果表明,相对于传统DTC控制方案,新型控制策略在稳态下能降低40%的转矩脉动,并保持较好的动态性能不变。进一步可以研究的方向为如何优化矢量合成算法,降低控制器的计算负担。
[1] 薛诚,宋文胜,冯晓云.五相永磁同步电机多目标优化直接转矩控制算法[J].中国电机工程学报,2016,36(6):1695-1704.
[2] 彭晟楠,刘小兵,龙驹.六相无刷直流电机分数阶PIλ,控制的分析与仿真[J].微特电机,2017,45(2):51-54.
[3] 鲍宇,耿乙文.6相感应电机的内模矢量控制系统研究[J].电气传动,2016,46(2):3-6.
[4] 艾永乐,王玉梅,KAMPERMarrten.梯形波相电流驱动六相感应电机建模与控制[J].电机与控制学报,2012,16(3):71-77.
[5] 耿乙文,鲍宇,王昊,等.六相感应电机直接转矩及容错控制[J].中国电机工程学报,2016,36(21):5947-5956.
[6] 郑剑,肖蕙蕙,李山.六相感应电机直接转矩控制系统[J].电机与控制应用,2010,37(11):15-19.
[7]ZHAOY,LIPOTA.SpacevectorPWMcontrolofdualthree-phaseinductionmachineusingvectorspacedecomposition[J].IEEETransactionsonIndustryApplications,1994,31(5):1100-1109.
[8] 张辑,彭彦卿,陈天翔.基于分类算法的双三相感应电机SVPWM[J].电力电子技术,2012,46(5):60-61.
[9] 张兴华,朱鹏程,李磊.感应电机直接转矩控制系统的滑模观测器设计[J].电气传动,2015,45(7):7-10.
[10] 刘少军,苑婷,姚欣欣,等.基于暂态磁链修正的直接转矩控制系统最大转矩输出方法[J].电机与控制应用,2017,44(1):12-17.
[11] 刘小勇,郑爱红.一种改进的异步电机直接转矩控制方法[J].电力电子技术,2016,50(9):44-47.
[12] 王斌,王跃,郭伟,等.基于定子磁链降阶状态观测的永磁同步电机无差拍直接转矩控制系统[J].电工技术学报,2014,29(3):160-171.
[13]HOANGKD,RENY,ZHUZQ,etal.Modifiedswitching-tablestrategyforreductionofcurrentharmonicsindirecttorquecontrolleddual-three-phasepermanentmagnetsynchronousmachinedrives[J].IETElectricPowerApplications,2015,9(1):10-19.
[14]RENY,ZHUZQ.Enhancementofsteady-stateperformanceindirect-torque-controlleddualthree-phasepermanent-magnetsynchronousmachinedriveswithmodifiedswitchingtable[J].IEEETransactionsonIndustrialElectronics,2015,62(6):3338-3350.
[15] 李政学,张永昌,李正熙,等.异步电机新型占空比直接转矩控制方案[J].电工技术学报,2015,30(24):23-31.
[16]RENY,ZHUZQ.Reductionofbothharmoniccurrentandtorqueripplefordualthree-phasepermanent-magnetsynchronousmachineusingmodifiedswitching-table-baseddirecttorquecontrol[J].IEEETransactionsonIndustrialElectronics,2015,62(11):6671-6683.
