运用蒙特卡洛模拟法的数据流调度优化模型研究∗

施 健 孟庆强 吕顺利

（南瑞集团公司（国网电力科学研究院） 南京 210024）

1 引言

随着信息通信技术的高速发展，特别是泛在物联网技术的普及应用，时时刻刻产生着海量、实时的数据流，面对这些“无限”运动着的数据，需要进行在线且精确的计算和分类，从而能够及时挖掘出其中隐含的有价值信息［1～3］。在云计算为代表的分布式流计算系统中，不仅包含了海量的静态、离线、结构化的数据，还有实时传输、持续生成的非结构化数据。为满足多任务并行处理的复杂计算需要，在分布式流计算系统中，将进行计算的海量数据切分成若干个小块数据流后交由多台计算机并行处理，并将局部计算结果整合得出最终结果。针对输入的同组数据流，其采用的调度算法不同，最终的计算效率差异非常大。

在传统的分布式处理模式中，输入的大多是静态数据，在利用有向无环图DAG（Directed Acyclic Graph）表示并行数据流在多处理机上进行任务调度时，其任务的执行时间是可预知的。由于分布式流计算系统中输入的是“无限"运动着的数据，而且这些数据的大小也是不确定的。这种不确定性的存在，使得传统的经典静态流据流调度方法将不再完全适用［4～5］。

本文提出一种运用蒙特卡洛模拟法的数据流任务调度方法，该方法利用随机数生成算法，在一定约束条件下大量模拟生成任务执行时间，通过经典的静态调度算法（HEFT）产生相应的预调度方案，经过综合比较最终得到一种最优的预调度方案。实验结果表明：本文提出的方法不仅大大缩短了任务的调度时间，而且具有非常强的通用性。

2 静态调度算法HEFT基本原理

异构计算最早完成时间（Heterogeneous Earli⁃est Finish Time，HEFT）算法［6］作为一种经典的针对异构计算资源的列表启发式静态数据流调度算法，目前已经得到广泛认可。

其主要思想分为两个阶段，第一阶段是任务优先级别的确定，根据任务的执行时间以及与后继任务的数据传输时间计算得到这个任务优先级别，并根据优先级别排序。第二个阶段是处理器的选择，根据第一个阶段得到的任务排序，选取未被调度的任务中优先级最高的任务，然后遍历所有可用资源，查找到能够最早完成处理该任务的计算资源，并将该任务分配到资源上相应的空闲时隙中。

HEFT算法在每一阶段都会选择向上权值rank最大的任务，并把选择出的任务分配给处理机，采用把任务插入到处理机空闲处的方法尽量减小最早完成时间。HEFT算法流程步骤见图1。

图1 HEFT算法流程图

但在分布式流计算系统中，输入源为实时动态的数据流，且数据量大小也是随机的，因此，HEFT算法在实际应用环境中，实验结果与预期结果差距较大。

3 基于蒙特卡洛模拟的改进算法

蒙特卡洛模拟MCS（Monte Carlo Simulation）方法［7～10］的核心思想是利用随机数，通过大量的随机取样实验来趋近数据的真实值，它已成为当前解决统计推断中模型拟合及优化问题的一种有效可行方法。本文提出利用蒙特卡洛模拟法，常采用反复的随机抽样来获得大量的随机样本，并通过计算所获得样本的结果来预测最优的预调度方案。

3.1 改进算法模型

设G=(N ，E ) 表示一组由节点N和一组边E组成的DAG有向无环图，形式都为(i →j) ，其中i，j∈N。节点i表示对应的任务，边i→j表示任务i和j之间任务间的依赖关系。G在处理机集合R上被调度，相应的改进算法流程如下：

1）定义输入空间：MCS的输入空间l是一组随机生成各任务在各处理机上执行时间的集合。定义如下：

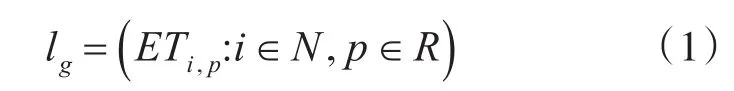
其中，ETi，p表示任务i在处理机 p上的确切执行时间。

2）随机抽样：针对输入空间lg中每个随机生成的任务执行时间进行抽样，得到样本函数，表示为fsmp(lg)：

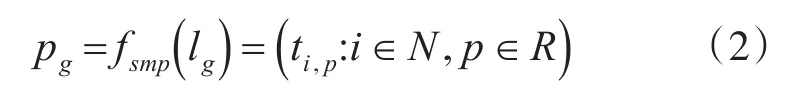
其中，ti，p是从 ETi，p中抽取的一个随机样本。

3）随机任务执行时间的均值：lg中每个具体任务在相应处理机上执行时间的平均值，其定义如下：

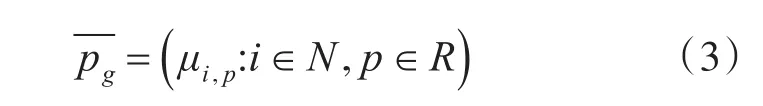
其中，μi，p为 ETi，p的期望值。

4）生成预调度方案：采用HEFT启发式静态调度算法对样本进行处理，得到一种静态预调度方案Ωg，定义如下：

选择预调度方案：每次从输入空间lg中随机抽取一样本，依次计算每种静态预调度方案Ωg的完工时间。

最后计算每种预调度方案的多个完工时间平均值，选出平均值最小的预调度方案。

改进算法实现

基于蒙特卡洛模拟的改进算法框架如下：

输入：带有随机生成任务执行时间lg集合的DAG应用g。

输出：最优预调度方案Ωg。

1）创建一个空的预调度方案列表L；

2）应用HEFT调度算法进行处理，得出平均预调度方案，并存入到L；

3）生成阶段：While不满足生成阶段的终止条件（重复m次），repeat；

4）在lg中取一个随机生成的任务执行时间样本 pg，其中包含g中各任务在不同处理机上执行时间的一组随机值；

5）应用启发式静态调度算法HEFT对任务执行时间样本 pg进行处理，最终生成相应的一种预调度方案Ωg；

6）把预调度方案Ωg存入L中，为后续计算最优平均完工时间做准备；

7）End While（每循环一次，就在lg中随机抽取一个新的样本 pg）；

8）选择阶段：for每一次循环（重复执行n次），do；

9）在lg中取一个随机生成的任务执行时间样本，其中包含lg中各任务在不同处理机上执行时间的一组随机值；

10）for针对L中存入的每一种预调度方案Ωg，do；

12）End for（L中每一种预调度方案采用的任务执行时间都是一样的，即都为）；

13）End fo（rL中每一种预调度方案都得到了n个不同的完工时间）；

14）经过选择阶段的循环计算后，对L中每一种预调度方案Ωg的 n个不同完工时间值求平均

MCS算法的复杂性完全依赖于生成阶段的启发式调度算法复杂度和选择阶段计算完工时间的算法复杂度。设带权任务有向无环图DAG，有节点v和边e，其在处理机P上被调度，则生成阶段和选择阶段重复的次度分别假定为常数m和n。生成阶段由于采用了HEFT算法，因此此阶段的算法复杂度为O(e p m )；选择阶段的算法复杂度为O(e n)。改进后的算法复杂度为O(e pm+en)。值，并把这个平均值作为平均完工时间；

15）Return取出拥有最小平均完工时间的预调度方案Ωg，作为最终要输甩出的调度方案；

16）end。

3.2 算法复杂度分析

4 算法验证与比较

为验证改进后算法的可行性，对HEFT算法和MCS算法进行了DAG调度的仿真。本文采用一个带有12个任务的典型DAG进行测试。图2展示出了DAG的结构和在两个相互依赖的任务之间进行传输的数据的大小。

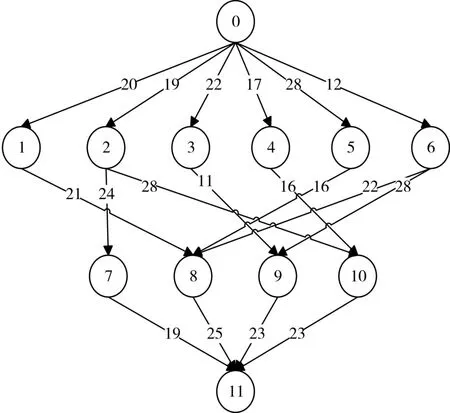
图2 DAG拓扑图

实验采用3台异构处理机，利用高斯分布（Gaussian distribution）分布建模随机生成任务执行时间，表1给出了每个随机任务执行时间的平均值μ，且随机变量设定在[ ]0.5μ，1.5μ 内，其标准偏差为0.167μ。

表2给出3台异构处理机之间的数据传输速率。

为验证改进后算法的性能，在生成阶段循环的重复次数为1000次，在选择阶段循环的重复次数为30次，且DAG启发式调度算法采用HEFT算法。

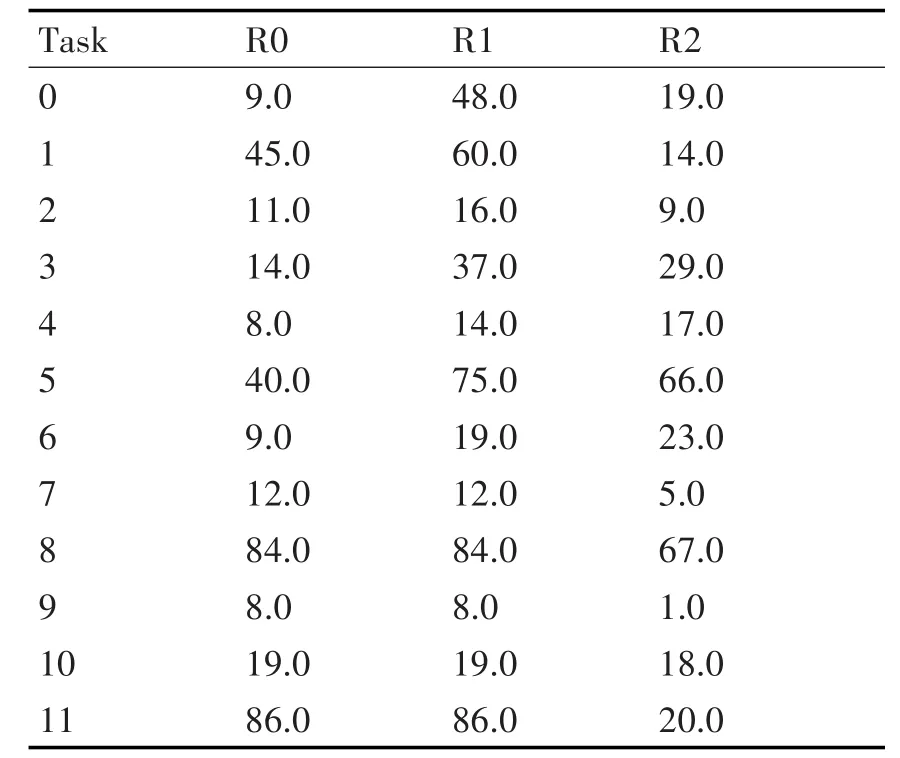
表1 三个异构处理机上各任务执行时间

表2 处理机间的传输率

图3为采用改进后算法得到的最优调度方案和采用传统HEFT算法得到调度方案。可见，在此典型的DAG图中，改进后算法的完工时间远小于传统HEFT算法的完工时间，性能提升在10%左右（改进后算法的调度完工时间约为163.5s，HEFT算法的调度完工时间约为181.5s）。

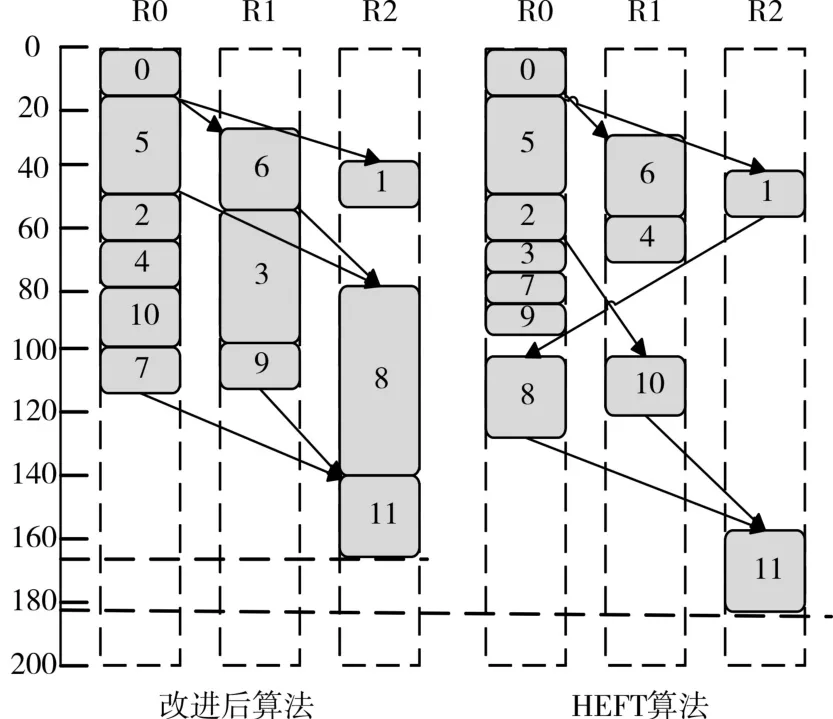
图3 两种算法得到的调度方案

实验结果表明此仿真的DAG图中，在静态启发式调度HEFT算法的基础上运用蒙特卡洛模拟改进算法，其结果优于只使用HEFT算法得到的静态调度方案。

5 结语

本文对传统的启发式静态调度HEFT算法进行了分析与研究，针对HEFT算法中存在的任务执行时间不确定性的问题，借鉴了Monte Carlo方法，改进后的算法在任务执行时间随机变化的情况下，获得一种性能较为优秀的平均完工时间调度方案。虽然改进后的算法其任务调度过程相对复杂，但相对那些在每个处理机上的每个任务执行时间预测值确定后才能进行启发式静态调度的算法而言，其具有较大的性能提升。

通过仿真环境对传统的HEFT算法和改进后的算法进行验证，实验结果表明改进后的算法能够获得一个较优的静态预调度方案，并且在任务执行时间预测值不准确的情况下运用改进后的算法，并没有产生过多的时间成本。在生成阶段没有太多随机抽样的情况下，也能找到一个好的调度方案，并且在选择阶段只需要进行很少数的随机抽样就能选出最佳的调度方案。

为使得调度算法能够具有较好地适用性，后续研究工作中应采用更多种不同类型的DAG进行进一步的优化甚至改进，同时，对蒙特卡洛模拟生成的随机数也可尝试采用更多种的概率分布为任务执行时间建模。

［1］Babeoek B，Babu S，Datar M．Models and Issues in Data Stream Systems［M］.In：Proc ofthe 21stACM SIGACT-SIGMOD-SIGART.New York： ACM Press，2002：1-16.

［2］WILHELM K，Evangelia K.Balancing load in stream pro⁃cessing with the cloud［C］//International Conference on Data Engineering，2011：16-21.

［3］ALFRED J，et al.A stream processing system simulator［C］//Workshop on Principles of Advanced and Distribut⁃ed Simulation，2010：97-105.

［4］HIROAKI S，et al.An adaptive high-availability scheme for distributed stream processing systems［C］//IEEE Inter⁃national Conference on Mobile Data Management，2010：413-418.

［5］NAZARIO C.Exploiting constraints to build a flexible and extensible data stream processing middleware［C］//Pro⁃ceedings of the 2010 IEEE International Symposium on Parallel and Distributed Processing，2010：356-359.

［6］H.Topcuoglu，S.Hariri，M.Wu，Performance-effective and low-complexity task scheduling for heterogeneous computing［J］.IEEE Trans.Parallel Distrib.Syst，2002，13（3）：260-274.

［7］丁明，李生虎，黄凯.基于蒙特卡罗模拟的概率潮流计算［J］.电网技术，2001（11）：10-14.DING Ming，LI Shenghu，HUANG Kai.Probabilistic load flow analysis based on Monte-Carlo simulation［J］.Power System Technology，2001，25（11）：10-14.

［8］刘炜，李群湛，唐兵，等.基于蒙特卡洛模拟的城市轨道概率潮流分析［J］.西南交通大学学报，2010，45（4）：561-567.LIU Wei，LI Qunzhan，TANG Bing，et al.Probabilistic Load Flow for Urban Rail Traction Power Supply Based on Monte Carlo Simulation［J］.Journal of Southwest Jiaotong University，2010，45（4）：561-567.

［9］Zhongming Y，Edward L，Yuen K H，et al.Probabilistic characterization of current harmonics of electrical traction power supply system by analytic method［J］.Iecon Pro⁃ceedings，1999，1：360-366.

［10］Rodrigues A B，Silva M G D.Probabilistic Assessment of Available Transfer Capability Based on Monte Carlo Method With Sequential Simulation［J］.Power Systems IEEE Transactions on，2007，22（1）：484-492.