基于FTSVM的固态发酵预测模型的研究∗

陈 树 任召金

（江南大学物联网工程学院 无锡 214122）

1 引言

固态酿酒过程中的酒醅发酵是决定出酒率的关键因数，而温度是衡量酒醅发酵过程优劣的最关键指标，高出酒率的发酵过程温度序列特性应有别于低出酒率的，一般酒醅发酵周期在两个月左右，仅一个窖池在一个发酵周期中就有近千个温度数据，面对多个周期和多个窖池，数据量是比较庞大的，为了从这些大量数据中分析与出酒率相关性，本文引入模糊孪生支持向量机建立预测模型［1］。

为了能有效地解决样本不均衡问题，Jayade⁃va［2］在2007年正式提出了孪生支持向量机（twin support vector machine，TSVM），TSVM的思想来自于广义特征值下的中心支持向量机（Generalized Eigenvalue Proximal Support Vector Machine，GEPS⁃VM）［3］，GEPSVM的核心思想是用两个非平行的超平面代替原来支持向量机的平行超平面，TSVM在GEPSVM的基础上改进了边界的限制，使得TSVM的速度比SVM提高了将近4倍，而分类的性能却能保持原来的精度，从TSVM的提出到现在，已经有了一系列的改进，文献［4］提出了最小二乘版的TS⁃VM，文献［5］提出了基于数据的结构信息的TSVM，文献［6］提出了拉普拉斯平滑TSVM的半监督分类；为了解决样本质量较低或者样本含有噪声对分类决策面的影响，文献［7］将模糊数学的概念引入到支持向量机中，提出了模糊支持向量机（Fuzzy Support Vector Machine，FSVM），FSVM的核心思想是对每个样本赋予一个隶属度，从而使得不同的样本得到不同的惩罚权重系数，对于位置处于中心的样本增加对分类决策面的作用，对于噪声或者孤立点削弱对分类决策面的作用，引入隶属度有效地降低了由样本噪声引起的不确定性，并提高了分类系统的鲁棒性。

在TSVM和FSVM思想的基础上，文献［1］提出了模糊孪生支持向量机（fuzzy twin support vector machine，FTSVM），FTSVM核心思想是为每个训练样本赋予不同的隶属度来构建两个最优非平行的分类决策面，为了减少孤立点或者噪声对非平行分类决策面的影响，进一步提高了分类器的性能。针对FTSVM对高维数据分类的效果不理想的情况，本文结合最小冗余最大相关算法（Minimum Redun⁃dancy Maximum Relevance，MRMR）和FTSVM算法，先对样本集进行特征提取降低样本的维度，再进行模糊孪生支持向量机训练。除此之外，针对样本内数据变化较为缓慢的情况，用单个样本数据集减去平均值并乘以权值以提高样本内数据的差异性，使得特征提取的子集更优，实验结果表明分类效果更好。

2 特征选择

特征选择是模式识别和数据挖掘领域的重要研究课题［8］，本质上可以看做是一个寻找最优的问题，而求解组合最优化问题最有效的方法就是采用搜索。到目前为止，已经有许多学者从不同的角度对特征选择进行了定义：Kira等［9］定义了理想情况下的特征选择是找到必要的、并且可以识别目标的最小特征子集；John等［10］认为特征选择是一个能够提高分类正确率，或者在不减少正确率的前提下降低特征的维度的过程；Koller等［11］认为在保证结果类分布尽可能与原始数据类分布相近的前提下，选择维度尽量小的特征子集。

本文采用最小冗余最大相关算法进行特征选择，但在特征选择之前，通过原始数据集减去单个样本平均值并且乘以一定的权值，使得样本内特征的差异变大，从而使特征提取的子集效果更好。MRMR特征提取是比较典型的基于空间搜索的过滤式方法，最大相关其实是指特征与类别的相关度最大，即特征能够最大程度地反映样本的类别信息；最小冗余是指特征内部的相关度最小。MRMR特征提取方法是用互信息作为度量特征的相关性和冗余度的标准，使用信息差和信息熵作为构建特征子集的搜索方法。其最大相关和最小冗余的定义分别如式（1）和式（2）所示：

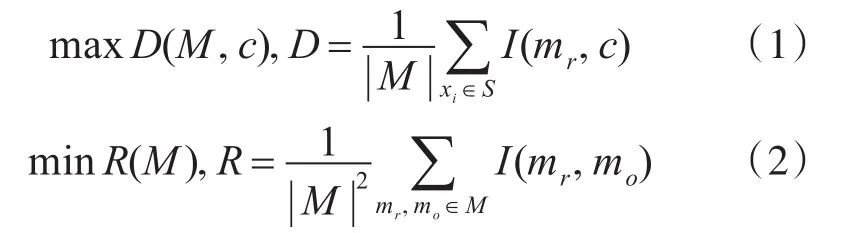
其中，M 为特征集合，c为样本标签，I(mr，c)表示特征mr与类别c之间的互信息，I(mr，mo)表示特征mr与特征mo之间的互信息。

给定两个随机变量X和Y，假设它们的概率密度分别为 p(x)，p(y)和 p(x，y)，则它们的互信息定义如式（3）所示：

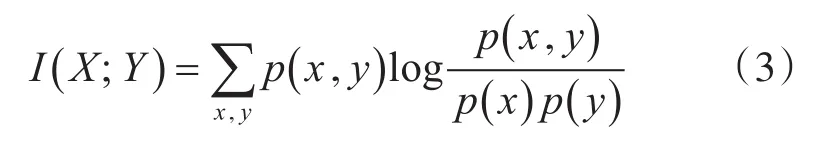
如果所选择的特征和输出类别之间的互信息越大，说明该特征子集包含的分类信息就越多，对分类识别就越有效。所以，通过计算互信息，可以很好地选择出包含分类信息最好的特征子集，提高分类的精度和效率。

最大相关最小冗余算法利用式（4）作为评价函数指导特征子集的选择。

其中，Q是特征与类别之间的互信息值，S是特征间的互信息的大小。

3 分类器

分类是数据挖掘领域中非常重要的一类方法，分类器（Classifier）是在已知数据的基础上构造出一个分类函数或者模型，该函数或者模型能够把数据映射到给定类别中的某一类，从而可以实现对数据的预测。总之，分类器是数据挖掘领域中对样本进行分类的方法的总称，常见的分类算法有决策树、朴素贝叶斯、支持向量机等［12］。

3.1 支持向量机

支持向量机是以统计学理论为基础的一种模式识别的方法，它将数据从低维空间映射到高维的特征空间，并在高维空间中寻找最优超平面作为判决面，将错分的风险降低到最小，从而使训练的模型具有更好的推广能力，即找到一个最优分类超平面能够将所有的训练样本分为两类，如不等式（5）所示：

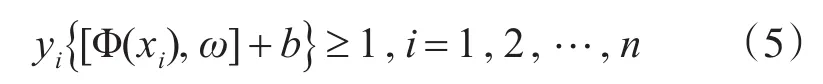
其中，n是训练样本的个数，yi表示标签。对于分类超平面而言，参数(ω，b)不是唯一确定的，但是一定有一对(ω，b)能使不等式（5）成立；针对离群点（可能是噪声）会造成超平面的移动，间隔缩小的情况，可以通过引入松弛变量 ξi，i=1，2，…，n ，则目标函数变为表达式（6）：

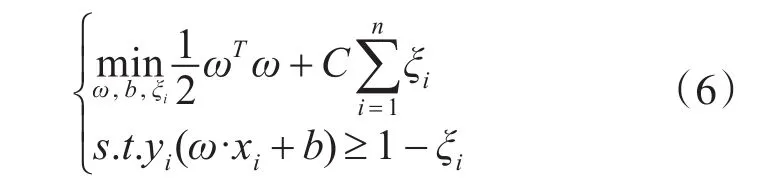
其中，ξi≥0，i=1，2，…l，C 为惩罚参数，表示对错误分类样本的惩罚参数，C的大小表示对错误分类的样本惩罚的约束，通过惩罚参数C可以调整错分样本的比例与算法复杂度的平衡。对于非线性情况，引入了核空间理论，设核函数的方程如（7）所示：

则二次规划问题的目标函数转变为方程（8）：

然后在此高维空间中寻找最优分割超平面，可用决策函数（9）来表示：

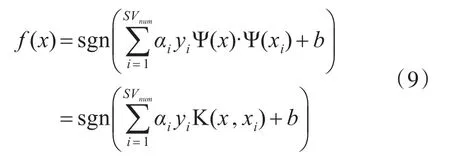
3.2 模糊支持向量机

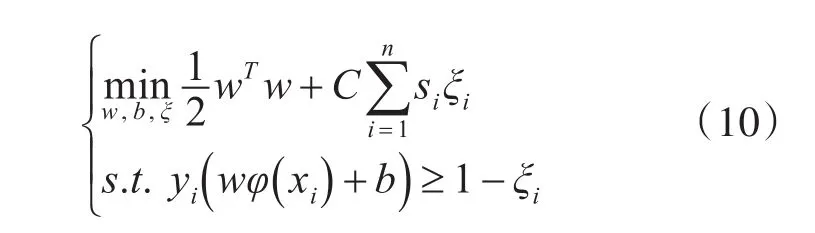
相应的二次规划的目标函数（8）转化为

模糊支持向量机的关键在于隶属度函数的设计，隶属度函数的构造方法有很多，迄今为止并没有一个标准的准则。根据文献［13］提供的思路来构建隶属度函数，由于正类和负类的隶属度定义类似，此处，只给出正类的模糊隶属度。特征空间H中的φpcen定义为

其中，φ()xj∈H表示任意输入数据点xj的转换，球半径的公式如（13）所示：

其中，δ＞0被定义为一个很小的常量，为了避免si+没意义，μ是范围在[ ]0，1的常数。

3.3 孪生支持向量机

与经典SVM不同的关键在于，TSVM由两个不平行的分类决策面组成，即

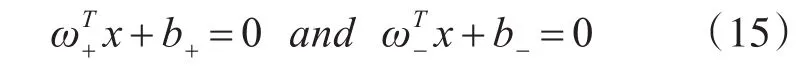
为了获取方程（15）的决策面，经典SVM的目标函数由式（6）转化为如下表达式：

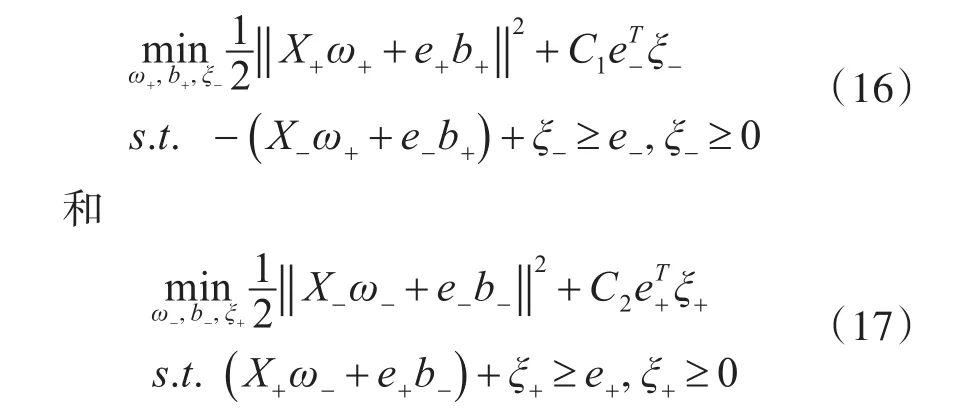
其中参数 C1＞0，C2＞0，ξ+和 ξ-分别表示正类和负类的松弛变量，e+，e-为单位行向量，其大小为正负类的样本大小。

3.4 模糊孪生支持向量机

模糊孪生支持向量机FTSVM集合了模糊支持向量机FSVM和孪生支持向量机TSVM的优点，从而使得分类效果更好，经典SVM的目标函数由式（6）转化为式（19）和式（20）：

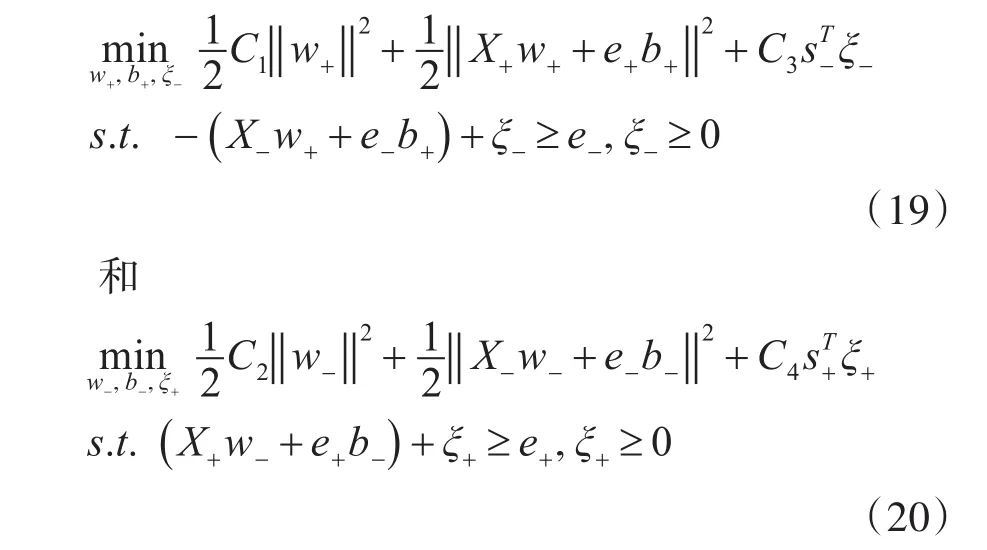
其中，s+∈Rl+和 s-∈Rl-都是由式（14）所表示的隶属度函数求得的模糊数向量，式（19）和式（20）的对偶问题为

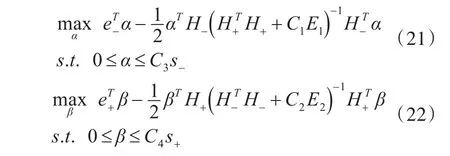
当非线性可分时，引入核函数k(x1，x2)=φ(x1)，φ(x2) ，所求的分类决策面为k(x ， XT)w++b+=0和k(x ， XT)w-+b-=0，FTSVM的目标函数转化为

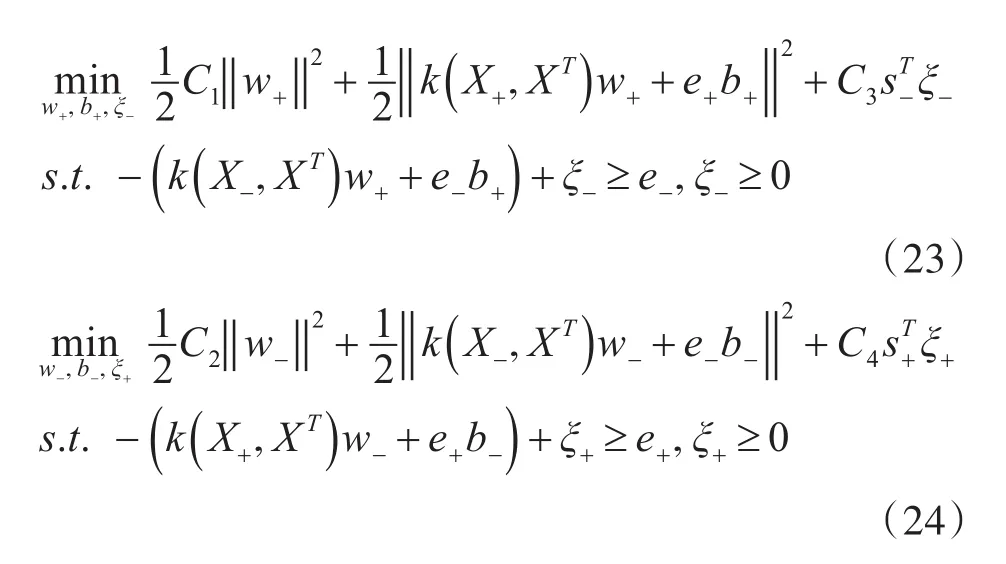
其对偶问题转化为

本文的算法流程图如图1所示。

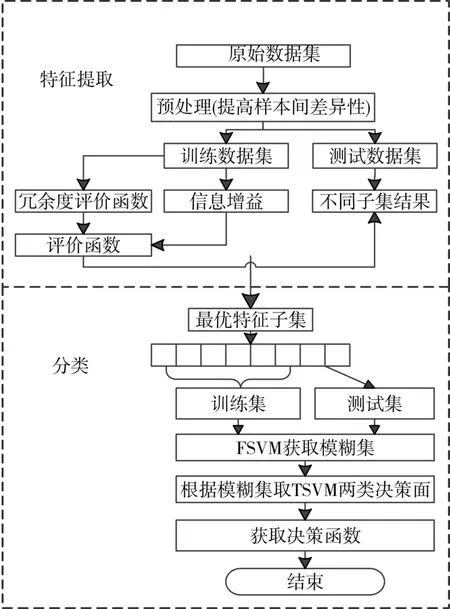
图1 本文算法实现流程图

4 实验结果及分析

实验分为两个部分，一是用模拟随机二维数据集检测算法的性能，数据集特征为400*2；另一部分是用某酒厂一年的生产发酵测温数据和产量数据作为本文算法的验证数据集，数据特征为572*1100。为了均衡输入样本中的特征的影响，每个特征会被归一化或者按比例缩小到［0，1］。通过为TSVM设置C1=C2在网格中仔细搜索模型参数ci( )i=1，2，3，4 ，网格搜索在10倍交叉验证中进行，随机选择全部样本的60%用做训练集，剩下的40%用做测试集。利用Matlab（R2014a）、MsSQL 2008、LibSVM 3.17和 Eclipse 4.4.1平台仿真，运行环境是Intel 3.30 GHz CPU，内存为4GB的PC机。

4.1 模拟数据集

模拟数据集有280个训练样本和120个测试样本，每个样本有2个维度，数据集总共分为两类。为了减少异常值数据对超平面的影响，令计算隶属度函数的式（14）的 μ=1。图2分别显示了线性和非线性情况下训练样本的模糊隶属度值的分布，如图2所示，与位于类中心附近的样本相比，远离类中心的样本的模糊隶属度总是更小，符合FSVM的核心思想。图3显示了TSVM与FTSVM在线性核和非线性核下的分类决策面。表1对比了模拟数据集在各个支持向量机下的预测准确率，其中，准确率是取5次预测结果的平均值，±号后面的结果是平均值与最小值或者最大值的最大误差，从表中可以看出，FTSVM的预测的稳定性要好于其他的支持向量机。

图2 模拟数据集中的训练样本的模糊隶属度分布

4.2 真实数据集

真实数据集为某酒厂一年的生产发酵测温数据和产量数据，每一个样本包含1100个温度数据，图4显示了不同产量下测温和时间的关系，每一个小图的纵坐标表示发酵的温度，横坐标表示从发酵开始所经过的小时数，在经过预处理且符合实验要求的样本中，选取342个正样本，230个负样本。按6：4随机划分训练集和独立测试集，Train（+）172个样本，Train（-）170个样本，Test（+）116个样本，Test（-）114个样本。图5对比了3组原始温度曲线和经过MRMR特征提取100维后的温度曲线，从图中可以看出MRMR特征提取的曲线可以刻画出原始曲线的走势，在维度较小的情况下，能够提取出尽量有效的信息。

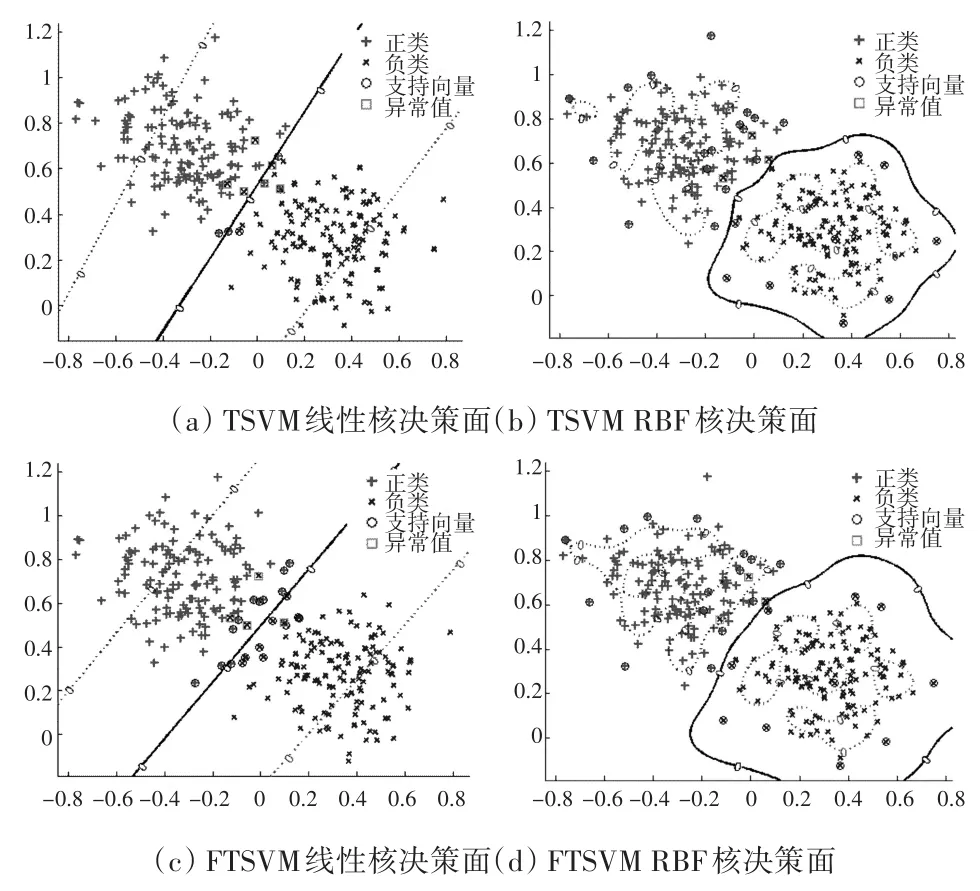
图3 TSVM与FTSVM在不同核函数下的决策面

表1 模拟数据集算法预测准确率对比

图4 不同产量下的温度发酵曲线

表2对比了线性核下各算法预测的准确率，其中，准确率是取5次预测结果的平均值，±号后面的结果是平均值与最小值或者最大值的最大误差，从表中可以看出，当维度较低时，本文算法的预测准确率要好于其他算法预测的准确率，在200维时，本文算法预测的平均准确率比经典SVM高17.5217%，比TSVM预测准确率高20.5217%，比FTSVM平均预测准确率高18.9565%；随着维度的增加，MRMR特征提取与原始数据的结果差不多，所以分类的效果也差不多。表3对比了RBF核下各算法预测的准确率，从表中可以看出，随着数据维度的增加MRMR-FTSVM的预测准确率却减小，因为训练集在经过RBF核函数映射过程是：Train（+，m+×l）、Train（-，m-×l）分别和Train（m×l）进行高维映射，映射后的数据集的为Train*（+，m+×m）、Train*（-，m-×m），跟原始训练集的维度没有关系，维度越高得到的映射矩阵斜对角线上的元素为1，其他元素趋于0，所以如果Train（+）或者Train（-）的维度大于样本个数就选用线性核。

图5 原始温度曲线与MRMR特征提取温度曲线对比

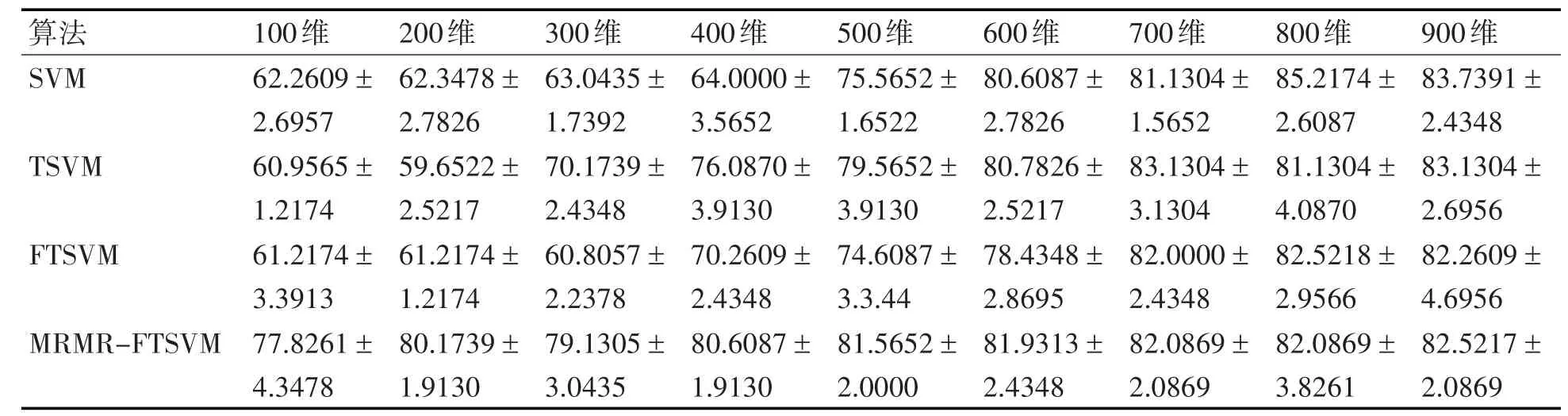
表2 线性核下各算法在不同维度下预测的准确率（%）

表3 RBF核下各算法在不同维度下预测的准确率（%）

5 结语

在实际的固态发酵过程中，根据温度数据对产量的高低进行预测能够有效地指导并改进生产工艺。传统的特征提取和SVM预测在实际应用中存在预测精度低的不足，本文提出了用原始数据样本集减去平均值并乘以一定的权重后，再进行MRMR特征提取，最后进行FTSVM预测的算法，有效地解决FTSVM在高维数据分类的不足，使用实际的数据集表明该方法能够真正地提高预测的准确率，并能实现提高产量的目标。

［1］Gao B B，Wang J J，Wang Y，et al.Coordinate Descent Fuzzy Twin Support Vector Machine for Classification［C］//IEEE，International Conference on Machine Learn⁃ing and Applications.2015：7-12.

［2］Jayadeva，，Khemchandani R，Chandra S.Twin Support Vector Machines for Pattern Classification［J］.IEEE Transactions on Pattern Analysis&Machine Intelligence，2007，29（5）：905-910.

［3］Mangasarian O L，Wild E W.Multisurface Proximal Sup⁃port Vector Machine Classification via Generalized Eigen⁃values［J］.IEEE Transactions on Pattern Analysis&Ma⁃chine Intelligence，2006，28（1）：69-74.

［4］Arun Kumar M，Gopal M.Least squares twin support vec⁃tor machines for pattern classification［J］.Expert Systems with Applications，2009，36（4）：7535-7543.

［5］Qi Z，Tian Y，Shi Y.Structural twin support vector ma⁃chine for classification［J］.Knowledge-Based Systems，2013，43（2）：74–81.

［6］Chen W J，Shao Y H，Hong N.Laplacian smooth twin support vector machine for semi-supervised classification［J］.International Journal of Machine Learning and Cyber⁃netics，2014，145（3）：459-468.

［7］Lin C F，Wang S D.Fuzzy support vector machines.［J］.IEEE Transactions on Neural Networks，2002，13（2）：464-71.

［8］姚旭，王晓丹，张玉玺，等.特征选择方法综述［J］.控制与决策，2012，27（2）：161-166.YAO Xu，WANG Xiaodan，ZHANG Yuxi，et al.A review of feature selection methods［J］.Control and Decision Making，2012，27（2）：161-166.

［9］Kira K，Rendell L A.The feature selection problem：tradi⁃tional methods and a new algorithm［C］//Tenth National Conference on Artificial Intelligence.AAAI Press，1992：129-134.

［10］John G H，Kohavi R，Pfleger K.Irrelevant Features and the Subset Selection Problem［J］.Machine Learning Pro⁃ceedings，1998：121-129.

［11］Koller D.Toward Optimal Feature Selection［C］//Proc.13th International Conference on Machine Learning.Mor⁃gan Kaufmann，2000：284-292.

［12］倪黄晶，王蔚.多类不平衡数据上的分类器性能比较研究［J］.计算机工程，2011，37（10）：160-161.LI Huangjing，WANG Wei.Comparison of Classifier Per⁃formance on Multiple Unbalanced Data［J］.Computer Engineering，2011，37（10）：160-161.

［13］Tang W M.Fuzzy SVM with a New Fuzzy Membership Function to Solve the Two-Class Problems.［J］.Neural Processing Letters，2011，34（3）：209-219.