融合多模型深层地应力预测方法∗

张文东 吕扇扇 张兴森 张卫东

（1.中国石油大学（华东）计算机与通信工程学院 青岛 266580）（2.中国石油大学（华东）石油工程学院 青岛 266580）

1 引言

地应力状态对油田油井的稳定性具有重要的意义，更是油气田勘探开发、油气井工程设计和施工的重要基础资料。但是由于研究手段和测试技术的限制，深层地应力很难测得，或者部分数据不理想［1～2］。如何利用少量的地应力资料来反演深层地应力场的问题一直是相关研究者研究的热点［3］。

孙炜锋、谭成轩等［4］将BP神经网络方法引入到应力场研究，采集了一些真实数据进行了拟合分析，并对深部的地应力做了预测，其实验结果表明了BP神经网络可以较好地建立地应力大小与各基本指标之间的相关关系，可以作为地应力大小预测的一种有效手段。郭喜峰、尹健民等［5］采用有限元回归分析，预测了部分重要工程部位在内的整个工程区岩体地应力场，其实验表明回归计算值能够较好地拟合实测值，表明这种基于有限元正演分析的多元回归反演方法是一种经济、可靠的方法。张广智、陈娇娇等［6］提出了适用于页岩地层的岩石物理等效模型的建立流程，并以此为基础实现了最小水平地应力的有效预测，建立的页岩气岩石物理等效模型具有更高的横波预测精度。Singha D K等［7］利用有限元模型预测的输出是应力大小和方向，包括建模误差，经实验证明了其可行性。赵小龙［8］运用了建立在统计学理论基础上的支持向量机（SVM）理论建立计算机模型，利用井场实测的水平最大应力和孔隙压力场是数据进行了拟合，模拟结果误差较小。

基于上述研究，本文提出融合多模型预测方法，该方法将多个子预测模型以投票优胜的策略融合在一起，有效克服由单个模型精度不满足工程需求的问题，并减小了拟合误差，达到了更好的预测效果。

2 融合多模型深层地应力预测

当前实现预测的机器学习算法很多，例如线性回归模型建立了两组变量间的线性因果关系，便于分析，但是其忽略了交互效应和非线性的因果关系。而BP神经网络［9～10］有自学习、推广和概括的能力，但其有可能会陷入过拟合而使预测效果不好。LS-SVM［11～12］有效抑制过拟合，以及利用内积核函数向高维空间非线性映射等优点，但是缺失了稀疏性。而本文中提出的方法通过各子模型之间的投票优胜，使各个子模型对于最终模型的预测值的贡献权重不同，有效克服由单个子模型预测精度不足的问题。

2.1 模型思想

主要思想：首先需要构建多个子预测模型，然后分别训练该子预测模型，训练集由随机选取的样本获得，而每个子预测模型对融合模型的最终预测结果的贡献值不一样，融合模型由多个子模型以投票优胜的策略融合一起。训练时某子模型的残差平方和的值越小，该子模型权重增加；否则，权重减少，得到最终融合模型，如图1所示。

2.2 融合多模型地应力预测方法

给定样本数据，假设

1）训练数据 X=(x1，x2，…，xn)，数据的实测值L=(l1，l2，…，ln)，xi为一个训练样本，li为该训练样本的实测值，其中i=(1，…，n)，n为训练样本数目；

图1 多模型算法模型示意图

2）fr(·)为单个子模型函数，r=(1，…，m)，m为子模型数目，子模型输出值F(·)为融合模型；

具体算法流程如下。

Step 1.从N个样本中选取n个样本X=(x1，x2，…，xn)进行模型训练，先将样本X输入到子模型，训练子模型 fr(·)，并得到各个子模型的预测值

Step2.将各个子模型的预测值Y=(Y1，Y2，…，Ym)输入融合模型 F(·)中，如式（1），训练融合模型，得到的误差为式（2）

按式（3）将误差函数J()θ对θ求偏导，得到每个θ对应的梯度：

由于是要最小化风险函数，所以按每个参数θ的梯度负方向，更新每个θ：

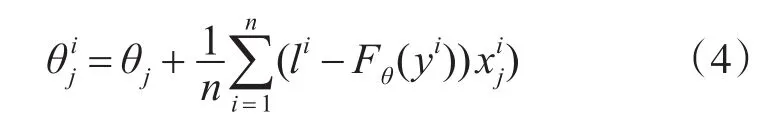
当误差达到设定阈值时，得到最终模型F(·)；

Step 3.将测试样本输入融合模型，得到预测值Z=(z1，z2，…，zs)，s为测试样本数目。

3 实验与分析

选取某油田实例实测数据进行分析，提取地层密度、静态泊松比、静态杨氏模量、内摩擦角、Biot系数、单轴抗拉强度、单轴抗压强度、断裂韧性、孔隙压力等9个参数［13］作为地应力状态预测研究的主要特征，对深层地应力进行实验预测。并将实验结果与LS-SVM、BP神经网络以及线性回归等地应力预测模型做了对比分析。为了便于分析比较，同时对预测模型的整体性能进行客观评价，定义以下误差指标［14～15］：

其中，N为预测样本数目，zi为第i个地应力样本的实测值，为第i个地应力样本的预测值，而希尔不等系数是表示拟合值和真实值之间的拟合程度，其值总是介于0～1之间，数值越小，表明其拟合程度越好，预测精度越高，当为0时，为100%拟合。

3.1 融合多模型地应力预测

从油田实测的35组样本数据中随机选取20个样本训练各个子模型，将各个子模型的预测值作为参数输入到融合模型中，再对融合模型进行优化，得到最终的模型。再选取剩余的15组数据作为预测样本，所得预测结果如图2，表1、2所示，从实验中我们可以看出：地应力预测中最小水平地应力和最大水平地应力预测拟合结果较好，并且有部分数据达到了重合，且最大水平地应力的平均相对误差为0.824%，最小水平地应力的平均相对误差0.919%，达到工程需求。

图2 水平地应力预测值

表1 融合多模型预测结果与地应力实测数据的比较

3.2 不同地应力预测方法的分析

将融合多模型预测方法与线性回归、BP神经网络和LS-SVM模型的预测结果进行了比较，最大水平地应力各预测方法如表2所示，从指标MRE来看，融合多模型预测方法较线性回归、BP神经网络、LS-SVM下降了0.029、0.03和0.003，总体上显示了较高的预测精度；指标RMSE可以评价数据的变化程度，融合多模型预测方法明显优于且较线性回归、BP神经网络、LS-SVM下降了1.614、1.704和0.095；通过指标TIC可以看出，融合多模型预测方法拟合结果明显好于线性回归、BP神经网络、LS-SVM。

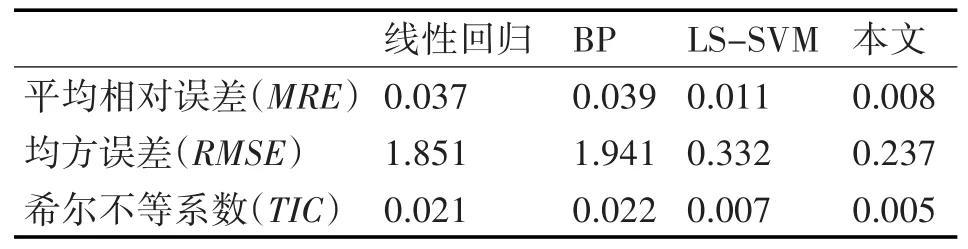
表2 最大水平地应力方法比较

从表3最小水平地应力方法比较中，也可以看出融合多模型预测方法较其他三种算法相比，MRE、RMSE、TIC三个误差指标均有所下降。由此可以看出，融合多模型预测方法结果较稳定，且较其他预测模型提高了预测精度。

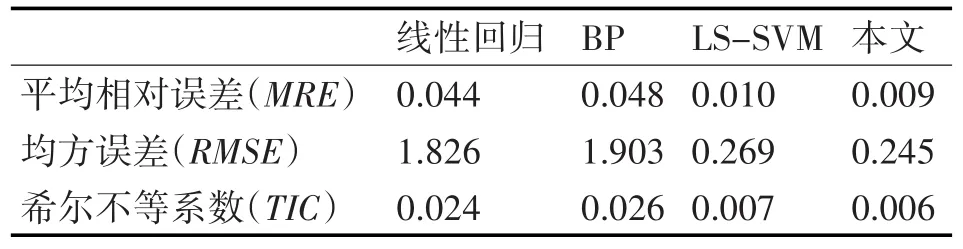
表3 最小水平地应力方法比较

4 结语

1）融合多模型预测方法作为智能岩石力学研究中的一种方法，可应用于岩石力学或工程中岩性不确定的深层地应力预测问题，是解决深层地应力问题的一种有效方法。

2）融合多模型预测方法较前人其他算法比较，精度得到了大大提升，拟合误差小，且增加了稳定性，说明该方法对地应力预测方面具有更大的应用价值。

3）温度不均、水压梯度、地表剥蚀或其它物理化学变化等也可引起相应的应力场，因此下一步研究应将更多影响地应力的因素考虑在内。

［1］李世海，李晓，刘晓宇.工程地质力学及其应用中的若干问题［J］.岩石力学与工程学报，2006，25（6）：1125-1140.LI Shihai，LI Xiao，LIU Xiaoyu.Some Issues in Engineer⁃ing Geomechanics and Its Application［J］.Chinese Jour⁃nal of Rock Mechanics and Engineering，2006，25（6）：1125-1140.

［2］王成虎.地应力主要测试和估算方法回顾与展望［J］.地质评论，2014，60（5）：971-996.WANG Chenghu.Brief Review and Outlook of Main Esti⁃mate and Measurement Methods for In-situ Stress in Rock Mass［J］.Geological review，2014，60（5）：971-996.

［3］练章华，曾久长，乐斌，等.油气井工程中地应力场反演研究的发展［J］.石油钻采工艺，2009，31（1）：1-5.LIAN Zhanghua，ZENG Jiuchang，LE Bin，et al.Develop⁃ment of Inversion Study on In-situ Stress Field in Petro⁃leum Engineering［J］.Oil Drilling&Production Technolo⁃gy，2009，31（1）：1-5.

［4］孙炜锋，谭成轩，王志明，等.基于BP神经网络的深埋隧洞地应力预测研究［J］.地质力学学报，2007，13（3）：227-232.SUN Weifeng，TAN Chengxuan，WANG Zhiming，et al.Prediction of Crustal Stress of Deep-Buried Tunnels Based on BP Artificial neural network［J］.Journal of Geo⁃mechanics，2007，13（3）：227-232.

［5］郭喜峰，尹健民，刘元坤，等.清远抽水蓄能电站地应力场有限元回归分析［J］.长江科学院院报，2008，25（5）：55-58.GUO Xifeng，YIN Jianmin，LIU Yuankun，et al.FEM Re⁃gression Analysis of In-situ Stress Field For Qingyuan Pumped Storage Power Plant［J］.Journal of Yangtze River Scientific Research Institute，2008，25（5）：55-58.

［6］张广智，陈娇娇，陈怀震，等.基于页岩岩石物理等效模型的地应力预测方法研究［J］.地球物理学报，2015，58（6）：2112-2122.ZHANG Guangzhi，CHEN Jiaojiao，CHEN Huaizhen，et al.Prediction for In-situ Formation Stress of Shale based on Rock Physics Equivalent Model［J］.Chinese Journal of Geophysics，2015，58（6）：2112-2122.

［7］Singha D K，Chatterjee R.Geomechanical modeling using finite element method for prediction of in-situ stress in Krishna-God4avari basin，India［J］.International Journal of Rock Mechanics&Mining Sciences，2015，73（5）：15-27.

［8］赵小龙.基于支持向量机的深层地应力预测模型［J］.特种油气藏，2016，23（1）：139-141.ZHAO Xiaolong.SVM Deep Geo-stress Prediction Model［J］.Special oil and gas reservoir，2016，23（1）：139-141.

［9］王洪元，史国栋.人工神经网络技术及其应用［M］.北京：中国石化出版社，2002.WANG Hongyuan，SHI Guodong.Artificial neural network technology and its application［M］.Beijing：China Petro⁃chemical Press，2002.

［10］夏战国，王珂，王志晓.基于网络复杂性的BP算法［J］.计算机工程与设计，2008，29（15）：3867-3869.XIA Zhanguo，WANG Ke，WANG Zhixiao.BP algorithm based on network complexity［J］.Computer Engineering and Design，2008，29（15）：3867-3869.

［11］顾燕萍，赵文杰，吴占松.最小二乘支持向量机的算法研究［J］.清华大学学报（自然科学版），2010，50（7）：1063-1066.GU Yanping，ZHAO Wenjie，WU Zhansong.Least Squares Support Vector Machine Algorithm［J］.Journal of Tsinghua University（Science and Technology），2010，50（7）：1063-1066.

［12］Wang Y，Guo W.Local prediction of the chaotic fh-code based on LS-SVM［J］.Journal of Systems Engineering and Electronics，2008，19（1）：65-70.

［13］李志明，张金珠.地应力与油气勘探开发［M］.北京：石油工业出版社，1997.LI Zhiming，ZHANG Jinzhu.Ground stress and oil and gas exploration and development［M］.Beijing：Petroleum Industry Press，1997.

［14］徐曼，乔颖，鲁宗相.短期风电功率预测误差综合评价方法［J］.电力系统自动化，2011，35（12）：20-26.XU Man，QIAO Ying，LU Zongxiang.A Comprehensive Error Evaluation Method for Short-term Wind Power Pre⁃diction［J］.Automation of Electric Power Systems，2011，35（12）：20-26.incremental Fisher discriminant analysis［J］.2004，2：757-760 Vol.2.

［15］高阳，张碧玲，毛京丽，等.基于机器学习的自适应光伏超短期出力预测模型［J］.电网技术，2015，39（2）：307-311.GAO Yang，ZHANG Biling，MAO Jingli，et al.Machine Learning-Based AdaptiveVery-Short-Term Forecast Model for Photovoltaic Power［J］.Power System Technol⁃ogy，2015，39（2）：307-311.