一种轴流风机的寿命预估方法*

吕 倩，乔纬韬

0 引言

在航空平台领域，电子设备主要有自然散热、风冷散热、液冷散热等散热方式。考虑到航空电子设备散热需求、成本、可维修性、技术成熟度等多方面综合因素的影响，空气冷却比液体冷却具备更简单、技术成熟度高，成本更低的优势，仍然是解决航空电子设备散热问题的重要途径。强迫风冷散热又可分为平台提供环控风和设备自带风机两种方式。轴流风机依然是航空独立电子设备散热的重要手段。电子设备产生的热量通过高速转动的轴流风机叶片产生的空气对流带走，风机成为整个散热系统的中枢环节。由于航空电子设备大量安装在非气密的设备舱室，因此作为设备重要部件的轴流风机也必须相应满足非气密舱室的温度、气压、电磁环境等各种恶劣环境条件的要求。因此，这些外部条件向航空平台轴流风机的环境适应性及可靠性设计提出了更高的要求。

航空平台轴流风机的工作温度范围为-55℃～+70℃，并且要耐受低气压、振动、冲击等环境因素的影响，因此航空平台轴流风机与普通工业品风机的寿命影响因子比较存在特殊性。

1 航空轴流风机的构成

航空轴流风机主要由扇叶、轴心、弹簧、滚珠、铁壳、磁环（钕铁硼）、上下线架、矽钢片、双层PCB板、扇框、垫片、卡簧等零组件构成，如图1所示。基本工作原理是：通过PCB板上的HALL传感元件感应钕铁硼磁环的位置，控制PCB板上的驱动芯片输出高电平或者低电平，继而控制MOS管打开及关断，从而控制缠绕在矽钢片上的漆包铜线上有无电流及电流方向。钕铁硼磁环磁极位置不断变化，导致漆包线上的电流方向不断变化，从而在马达周围产生不断变化的电磁场，钕铁硼在磁力的作用下驱动轴芯及扇叶持续同一方向高速运动[1]。

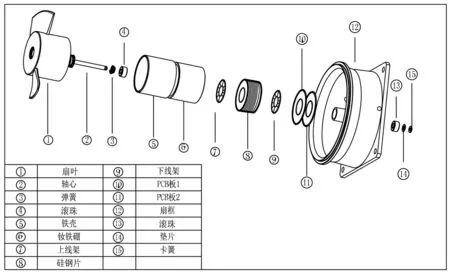
图1 某型号轴流风机爆炸图

从轴流风机的组成来看，电路板上元器件失效和电机的转动磨损是影响其可靠性的关键因素，且这两种失效机理互不影响。

2 轴流风机寿命预估依据

轴流风机的寿命预估主要依据两项指标（L10与MTTF）。目前工业品普遍依据IPC9591标准中的规定[2]。L10和MTTF所需实验时间和样本数量如表1所示，按IPC9591标准，如果要评价航空轴流风机的寿命，实验的时间长度和样本数，至少需要60个样品进行324天的实验[3]。考虑到试验的可实施性及试验数据的准确性，考虑到加速试验的可实施性，本次试验拟采用温度加速的方式，针对电子元器件计算加速系数。机械部分没有加速效应。

试验结束后，对失效数据进行分析，将故障分为电子元器件失效和机械疲劳失效两部分分别进行评估，最终以寿命较短者作为产品的寿命。

3 电子部分加速系数确定方法

温度应力下电子部件加速因子评估首先利用Arrhenius阿伦尼斯模型评估出各组成元器件在温度可靠性加速试验条件下相对于正常应力温度下的加速系数，再按照电子部件的基本可靠性模型求解得到加速系数。

Arrhenius阿伦尼斯模型评估元器件的加速系数如下。

温度的加速因子由Arrhenius阿伦尼斯模型计算所得：

Acc——温度Ta相对于Tu的加速系数；

Ea——激活能，以eV为单位，根据IEC61709、IEC62380、IPC279、GJB299C等标准及元器件试验值和相关文献获取。

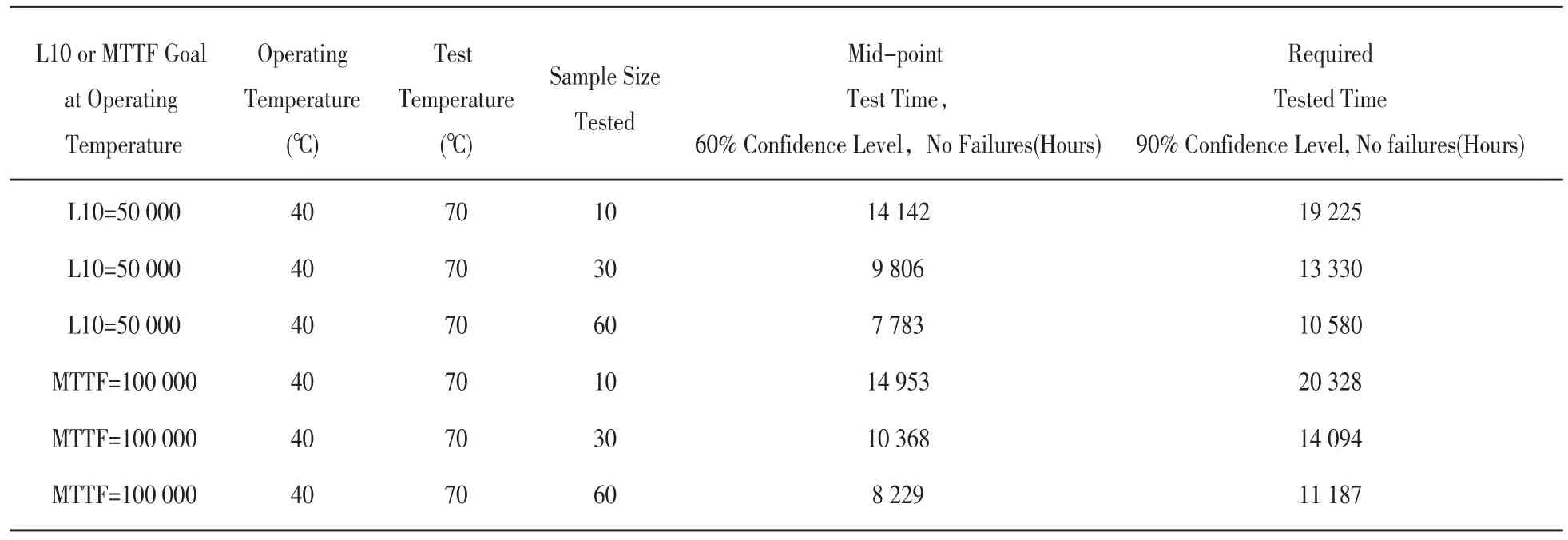
表1 IPC9591标准试验时间

K——玻尔兹曼常8.6171×105V K。

加速系数是产品在正常应力水平下达到某一失效概率所经历的试验时间，与产品在加速应力水平下达到相同失效概率所经历的试验时间之比[4-5]。

那么对于失效时间服从指数分布的电子产品，失效率为常数，其失效概率函数为：

F（t） =1-eλt

式中，λ为失效率。

假设在正常应力水平s0下的某元器件的失效分布函数为F0（t），失效率为 λ0，tp，0为失效概率达到p的时间，即F0（tp，0）=p，又设该元器件在加速应力水平si下的失效分布函数为Fj（t），失效率为λj，tp，j为失效概率达到p的时间，即Fj（tp，j）=p。

根据加速系数τ1的定义，则：

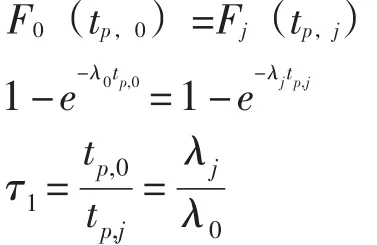
在所有电子元器件的寿命分布都服从指数分布的前提下，根据基本可靠性的串联模型，各个单元的失效率等于包含的所有元器件失效率之和，产品的失效率等于各个单元的失效率之和，可得系统失效率等于所有元器件失效率之和[6]：

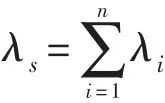
因此，电子部件高温保持加速因子为：

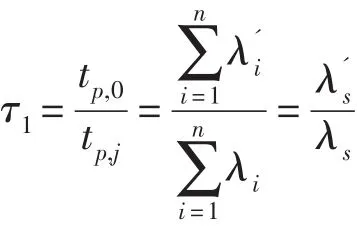
式中，

λi——在正常应力水平下第i个组成单元的失效率；

i效率；

λs——在正常应力水平下产品的失效率；

n——组成产品的单元数。

4 加速条件及加速系数

利用3提供的方法，高速风扇在各温度和各转速条件下对于70℃和55℃环境条件下的加速系数见表2[7]。

表2 高速风扇可靠性加速试验加速系数预估

5 试验样本量和截至条件

本次高速风扇加速试验样本量选为10只，达到以下条件之一，可以结束试验：

（1）有至少2个产品因机械疲劳失效；

（2）有至少1个产品因电子元器件失效。

6 可靠性的评估

6.1 电子部分可靠性评估

假设高速风扇因电子部分而失效的时间样本为x1、x2，…，xr，则其置信度0.7的MTBF评估值为：

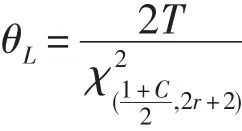
其中：

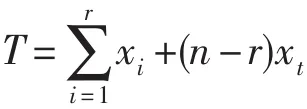
xt为无故障风机运行时间，xi为故障风机失效前运行时间，r为故障风机数量。

故其L10寿命值为[8-9]：

L10=-θLln0.9

6.2 机械部分可靠性评估

滚珠轴承的寿命决定了整个机械部分的寿命。经计算，滚珠轴承的L10寿命为13 452小时（风扇叶片加工精度0.2 mm）。所以理论上，13 452小时内，10个样本中至多有1支风扇因机械磨损而失效。

如果在试验结束前没有出现机械类故障，则以理论计算值代替评估值；如果存在机械故障，利用威布尔理论进行评估。

威布尔分布参数的极大似然估计可以通过下面方程的数值解得到。满足公式（1）的解就是β的极大似然估计，这个解代入式（2）解出η的极大似然估计[10-11]。

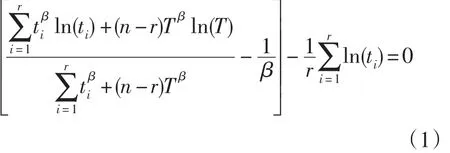
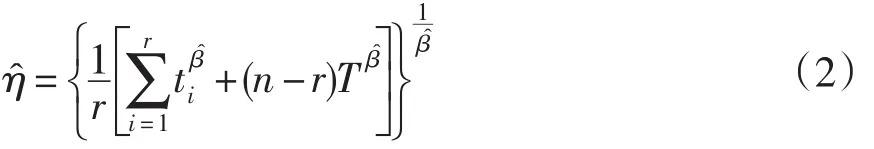
失效分位数（10%）的点估计

6.3 风扇可靠性评估

在分别对风扇电子部分和机械部分进行可靠性估计后，因为两部分的故障是相互独立的，风扇L10寿命=min(（电子部分L10，机械部分L10）。

7 结束语

参照IPC9591标准，对风机实验的时间和样本数的要求都极为苛刻，因此考虑采用温度加速实验来降低实验时间成本。

本文借助Arrhenius模型评估电子元器件的加速系数，对温度加速实验结果进行分析即可等效得出常规风机实验结果。风机的故障失效原因可分为电子元器件失效和机械疲劳失效；分别根据风机实验结果对其进行可靠性分析，风机电子部分和机械部分L10寿命的最小值即为风机的L10寿命。

本文为通过实验预测风机寿命提供了一种新思路，对风机进行温度加速实验可以大大减少整个实验的时间，并可以通过可靠性评估对轴流风机的寿命做出准确预测。

参考文献：

［1］杨诗成.轴流风机［M］.北京：水利电力出版社，1995.

［2］Michael G.Pecht.可靠性工程基础［M］.北京：电子工业出版社，2011.

［3］ Oh H，Azarian M H，Das D，et al.A Critique of the IPC-9591 Standard：Performance Parameters for Air Moving Devices［J］.IEEE Transactions on Device&Materials Reliability，2013，13（1）：146-155.

［4］黄宝胜，刘爱翠，李国英.阿伦尼斯模型下可靠性增长数据的统计分析［J］.工程数学学报，2005，22（5）：807-814.

［5］林震，姜同敏，程永生，等.阿伦尼斯模型研究［J］.电子产品可靠性与环境试验，2005，23（6）：12-14.

［6］李晓莉，张雅文.概率论与数理统计［M］.北京：高等教育出版社，2014.

［7］范志锋，齐杏林，雷彬.加速可靠性试验综述［J］.装备环境工程，2008，5（2）：37-40.

［8］ Surface， N.Handbook of Reliability Prediction Proce⁃duresfor Mechanical Equipment［M］.Maryland：CAR⁃DEROCKDIV，2006：15-47.

［9］张群林，卢金玲，毛义军.基于单向流固耦合的轴流风机强度分析与寿命预测［C］.西安：中国工程热物理学会，2014：1-14.

［10］王金晓，于良，WANGJin-xiao，等.基于Weibull模型的风机变桨器短期可靠性分析［J］.通信电源技术，2016，33（4）：68-70.

［11］刘智敏.产品寿命研究中韦布尔分布的应用方法［J］.数学的实践与认识，1979（3）：33-40.