卢道隆记里鼓车的两个数据问题
2018-04-25程军
程 军
(中国科学技术馆,北京100012)
1 问题的起源
记里鼓车是我国古代的一项重要发明,古籍中多有记载。
《晋书》卷二十五记道:“指南车过江亡失,及义熙五年,刘裕屠广固始复获焉,乃使工人张网补辑周用。十三年,裕定关中,又获司南记里诸车,制度始备。”“记里鼓车,驾四,形制如司南,其中有木人执槌向鼔,行一里则打一槌。”[1]
《宋书》卷十八记道:“记里车,未详所由来,亦高祖定三秦所获,制如指南,其上有鼓,车行一里木人则击一槌。大驾卤簿以次指南。”[2]
《南齐书·舆服志》《古今注》《隋书·礼仪志》《旧唐书·舆服志》《唐书·车服志》对记里鼓车也有简略的记载。
以上这些记载都没有涉及到记里鼓车的内部构造。
对记里鼓车的内部构造有记载的是《宋史》《愧郯录》等文献,它们记载了卢道隆记里鼓车和吴德仁记里鼓车。卢道隆记里鼓车是现存最早的有内部构造记载的记里鼓车。
学术界研究卢道隆记里鼓车都是以《宋史》为依据。
下面先介绍《宋史》中记载的卢道隆记里鼓车。
《宋史》卷一百四十九记道:“记里鼓车,一名大章车,赤质,四面画花鸟,重台,勾阑,镂拱。行一里,则上层木人击鼓;十里,则次层木人击镯。一辕,凤首,驾四马,驾士旧十八人,太宗雍熙四年,增为三十人。仁宗天圣五年,内侍卢道隆上记里鼓车之制。独辕,双轮,箱上为两重,各刻木为人,执木槌。足轮各径六尺,围一丈八尺,足轮一周而行地三步。以古法六尺为步、三百步为里,用较今法五尺为步、三百六十步为里。立轮一附于左足,径一尺三寸八分,围四尺一寸四分,出齿十八,齿间相去二寸三分;下平轮一,其径四尺一寸四分,围一丈二尺四寸二分,出齿五十四,齿间相去与附立轮同;立贯心轴一,其上设铜旋风轮一,出齿三,齿间相去一寸二分;中立平轮一,其径四尺,围一丈二尺,出齿百,齿间相去与旋风等;次安小平轮一,其径三寸少半寸,围一尺,出齿十,齿间相去一寸半;上平轮一,其径三尺少半尺,围一丈,出齿百,齿间相去与小平轮同。其中平轮转一周,车行一里,下一层木人击鼓;上平轮转一周,车行十里,上一层木人击镯。凡用大小轮八,合二百八十五齿,递相钩鏁,犬牙相制,周而复始。诏以其法下有司制之。”[3]
仁宗天圣五年是1027年。
这里“径”指轮直径,“围”指轮周长。
从“足轮各径六尺,围一丈八尺”、“径一尺三寸八分,围四尺一寸四分”等数据可知,卢道隆记里鼓车是将圆周率取为3。
其中“小平轮”“围一尺,出齿十”,即周长为一尺,一周有10个齿。
因为 1尺=10寸,所以“小平轮”齿间距应为“一寸”。
《宋史》记载“小平轮”“齿间相去一寸半”是错误的,应为“齿间相去一寸”。这从下面将介绍的《太常因革礼》《愧郯录》《文献通考》中的文字也可得到印证。
对这段文字最早进行研究的是张荫麟。张荫麟于1925年对这段文字做了研究,绘出了卢道隆记里鼓车的结构图,并对此车的数据进行分析。张荫麟认为“文中所记小平轮,及上平轮之径围,俱有差误。‘三寸少半寸’一语,亦殊费解,如解作二寸五分;则周围当合七寸五,与‘围一尺’及‘齿间相去一寸半’俱不合;如解作三寸又半寸,或三寸半稍不足,则与围一尺之说尚可相通,惟与齿距寸半之说,仍未能相符。‘径三尺少半尺’语,亦同一费解。”[4]
王振铎对“三寸少半寸”的理解与张荫麟基本相同。王振铎认为:“文中记各齿轮之直径大小多有不可理解者,如记小平轮云:‘其径三寸少半寸’,如解作二寸五分,则轮周当合七寸五分,与‘围一尺’及‘齿间相去一寸半’俱不合;如解作三寸又半寸,或三寸稍不足,惟与齿距半寸之说,仍未能符合。”[5]
刘仙洲认为《宋史》中记载的卢道隆记里鼓车和吴德仁记里鼓车的构造,“按齿数计算都是合理的,惟所记的各齿轮的周节多有不合者”,“记载上有不少错误是毫无疑义的”。[6]“周节”指齿间距。
陆敬严等人在《中国科技技术史·机械卷》中介绍卢道隆记里鼓车和吴德仁记里鼓车时也提到“文献中关于齿间相去数据的记载,有的存在着问题,未必准确。”[7]
李约瑟在对《宋史》中这段话解释时,将“三寸少半寸”解释为“3.3寸”,将“三尺少半尺”解释为“3.3尺”,但没有给出理由。[8]
除了《宋史》以外,《太常因革礼》《愧郯录》《文献通考》也记载了卢道隆记里鼓车。
2 《太常因革礼》《愧郯录》《文献通考》对卢道隆记里鼓车的记载
2.1 《太常因革礼》记载的卢道隆记里鼓车
《太常因革礼》卷二十二记道:“天圣五年十一月内侍卢道隆上言明记里鼓车。其车独辕,双轮,厢上为两层,各安木人,手执木搥(应为“槌”?)。脚轮各径六尺,围一丈八尺,脚轮一周而行地三步。古法六尺为步,三百步为里;今法五尺为步,三百六十步为里。立轮一只,附于左脚,径一尺三寸八分,围四尺一寸四分,出齿十八,齿相去二寸三分;下平轮一只,径四尺一寸四分,围一丈三(应为“二”?)尺四寸二分,出齿五十四,齿间相去与附立轮同;立贯心轴一条,上安铜旋风轮一枚,出齿三,齿间相去一寸二分;中立平轮一只,径四尺,围一丈二尺,出齿百,齿间相去与旋风轮等;次安小平轮一只,径三寸少半寸,围一尺,出齿十,齿间相去一寸;上平轮一只,径三寸(应为“尺”?)少半尺,围一丈,出齿百,齿间相去与小平轮同。其中平轮转一周,车行一里,下一层木人击鼓;上平轮转一周,车行十里,上一层木人击觸(应为“镯”?)。都用大小轮八只,共二百八十五齿,递相钩鏁,犬牙相制,周而复始。亦诏有司依此制造。”[9]
《太常因革礼》是北宋欧阳修、苏洵等人所撰,成书于北宋治平年间(1064-1067),记载了宋代建隆至嘉祐年间的礼典,距卢道隆上记里鼓车之制的时间1027年仅约40年。《太常因革礼》是目前所知最早记载卢道隆记里鼓车的。
2.2 《愧郯录》记载的卢道隆记里鼓车
《愧郯录》卷第十三记道:“指南则始于 天圣五年十一月壬寅,定王府记室参军工部郎中直昭文馆燕肃创意,始上其制……是时入内内侍省内侍殿头卢道隆,亦上记里鼓之制。其车亦独辕,双轮,箱上为两层,各安木人,手执木槌。脚轮各径六尺,围一丈八尺,脚轮一周而行地三步。古法六尺为步,三百步为里;今法五尺为步,三百六十步为里。立轮一只,附于左脚,径一尺三寸八分,围四尺一寸四分,出齿十八,齿间相去二寸三分;下平轮一只,径四尺一寸四分,围一丈二尺四寸二分,出齿五十四,齿间相去与附立轮同;立贯心轴一条,上安铜旋风轮一枚,出齿三,齿间相去一寸二分;中立平轮一只,径四尺,围一丈二尺,出齿百,齿间相去与旋风等;次安小平轮一只,径三寸少半寸,围一尺,出齿十,齿间相去一寸;平轮一只,径三尺少半尺,围一丈,出齿百,齿间相去与小平轮同。其中平轮转一周,车行一里,下一层木人击鼓;上平轮转一周,车行十里,上层木人击镯。都用大小轮八只,共二百八十五齿,递相钩锁,犬牙相制,周而复始。”[10]
《愧郯录》是南宋岳珂所撰,成书于1214年。
2.3 《文献通考》记载的卢道隆记里鼓车
《文献通考》也记道:“天圣间内侍卢道隆上记里鼓车之制,其制独辕,双轮,箱上为两重,各刻木为人,执槌。足轮各径六尺,围丈八尺,足轮一周而行地三步。以古法六尺为步、三百步为里,用较今法五尺为步、三百六十步为里。立轮一附于左足,径一尺三寸八分,围四尺一寸四分,出齿十八,齿间相去二寸三分;半(应为“下”?)平轮一,其径四尺一寸四分,围丈二尺四寸二分,出齿五十四,齿间相去与附立轮同;立贯心轴一,其上设铜旋风轮一,出齿三,齿间相去寸二分;中立平轮一,其径四尺,围丈二尺,出齿百,齿间相去与旋风等;次设小平轮一,其径三寸少半寸,围一尺,出齿十,齿间相去一寸;上平轮一,其径三尺少半尺,围一丈,出齿百,齿间相去与小平轮同。其中平轮转一周,车行一里,(脱漏“下”?)一层木人击鼓;上平轮转一周,车行十里,上一层木人击镯。凡用大小轮八,合二百八十五齿,递相钩鏁,周而复始。”[11]
《文献通考》为元代初年马端临(1254-1323)所撰。
将《太常因革礼》《愧郯录》《文献通考》中有关卢道隆记里鼓车的文字和《宋史》中有关卢道隆记里鼓车的文字相比较,可以看出它们基本相同。
相应于《宋史》中“次安小平轮一,其径三寸少半寸,围一尺,出齿十,齿间相去一寸半”的记载,
《太常因革礼》记载的是“次安小平轮一只,径三寸少半寸,围一尺,出齿十,齿间相去一寸”;
《愧郯录》记载的是“次安小平轮一只,径三寸少半寸,围一尺,出齿十,齿间相去一寸”;
《文献通考》记载的是“次设小平轮一,其径三寸少半寸,围一尺,出齿十,齿间相去一寸”。
这四种古籍对“小平轮”直径的记载都是“三寸少半寸”,它们都记错的可能性不大。
另外,《太常因革礼》《愧郯录》《文献通考》对“小平轮”齿间距的记载都是“齿间相去一寸”,与上文分析的“小平轮”齿间距的数值相合。
“三寸少半寸”是比“三寸”少了“半寸”?还是“三寸”再加上“少半寸”?
如将“三寸少半寸”解释为“三寸”少了“半寸”,则“小平轮”的周长应为七寸半,与“围一尺”不合。而且这样的解释也不符合古人对数据的记载方式。
按照古人对数据的记载方式,应该是“三寸”再加上“少半寸”,那“少半寸”是多少?
3 “少半”的含义
唐代李籍在《九章算术音义》中记载了“少半”:“半,博漫切,物中分也。凡言半者,以二为分母;言太半、少半者,以三为分母。”[12]
就是说,“半”是以二为分母,“太半”“少半”是以三为分母。“少半”究竟是三分之几?
《夏侯阳算经》和《算学启蒙》也记载了“少半”。
唐朝初年李淳风注释的十部算经中有《夏侯阳算经》,传本《夏侯阳算经》含有唐朝中期的若干史料,不是原本。[13]
《夏侯阳算经》卷上“明乘除法”对“少半”有明确的记载:“二分之一为中半,三分之二为太半,三分之一为少半,四分之一为弱半。此漏刻之数也。”[14]
《算学启蒙》是元代朱世杰所撰,刊刻于1299年。《算学启蒙》“总括”对“少半”也有明确的记载:“二分之一为中半,三分之一为少半,三分之二为太半,四分之一为弱半,四分之三为强半。”[15]
可见,“少半”即三分之一。
4 一个带有“少半”的例题
下面举1个古代数学题中含有“少半”的例子。
《九章算术》约编成于公元前1世纪中叶,书中有一些题目中含有“少半”。
《九章算术》卷二“粟米”有:
“粟米以御交质变易:粟率五十,粝米三十,粺米二十七……菽、荅、麻、麦各四十五……蘖一百七十五。今有术曰:以所有数乘所求率为实,以所有率为法。”[16]
这段话讲的是谷物(或其制成品)之间的交换率。
假如有五十斤粟,则可换三十斤粝米,可换二十七斤粺米……可换菽、荅、麻、麦各四十五斤……可换一百七十五斤蘖。
此卷有1道题是:
“今有粟三斗少半升,欲为菽,问得几何?答曰:为菽二斗七升一十分升之三。”[17]
根据这段文字可知:粟三斗少半升,如果换成菽,则得二斗七升一十分升之三。
因为1斗=10升,
设换成的菽为x升,
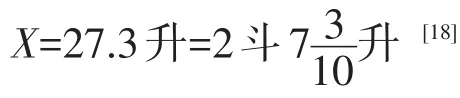
这与题目的答案“二斗七升一十分升之三”是吻合的。
5 “三寸少半寸”“三尺少半尺”的正确解释
由上面的介绍可知,我国古代将三分之一称为“少半”,而按照古人对数据的记载方式可知,“径三寸少半寸”就是直径为“三寸”再加上“少半寸”。
因为1尺=10寸,所以“小平轮”周长为“一尺”。
这与《宋史》《太常因革礼》《愧郯录》《文献通考》对“小平轮”周长的记载相合。
所以,“上平轮”周长为10尺。
因为10尺=1丈,所以“上平轮”周长为1丈。
这与《宋史》《愧郯录》《文献通考》对“上平轮”周长的记载相合。
因为圆周率取为3,所以当直径为
[1][唐]房玄龄.晋书(卷二十五)[M].文渊阁四库全书.第255册.台北:商务印书馆,1983:448,456.
[2][梁]沈约.宋书(卷十八)[M].文渊阁四库全书.第257册.台北:商务印书馆,1983:305.
[3][元]托克托.宋史(卷一百四十九)[M].文渊阁四库全书.第282册.台北:商务印书馆,1983:641-642.
[4]张荫麟.宋卢道隆吴德仁记里鼓车之造法[J].清华大学学报(自然科学版),1925,2(2):635-642.
[5]王振铎.科技考古论丛[M].北京:文物出版社,1989:31.
[6]刘仙洲.中国在传动机件方面的发明[J].机械工程学报.1954.2(1):1-27.
[7]陆敬严,华觉明.中国科学技术史·机械卷[M].北京:科学出版社.2000:99-101.
[8]李约瑟,王玲.中国科学技术史第四卷(第二册)机械工程[M].北京:科学出版社,1999:311.
[9][宋]欧阳修.太常因革礼(卷二十二)[M].续修四库全书.第821册.上海:上海古籍出版社.2002:435.
[10][宋]岳珂.愧郯录(卷第十三)“指南记里鼓车”[M].四部丛刊续编(五四).上海:上海书店,1984:12.
[11][元]马端临.文献通考(卷一百十七)[M].文渊阁四库全书.第612册.台北:商务印书馆,1983:733-734.
[12][唐]李籍.九章算术音义[M].文渊阁四库全书.第797册.台北:商务印书馆,1983:132.
[13]郭书春,李兆华.中国科学技术史·数学卷[M].北京:科学出版社,2010:351.
[14]夏侯阳.算经(卷上)[M].郭书春.中国科学技术典籍通汇·数学卷(第一册).郑州:河南教育出版社,1993:381.
[15][元]朱世杰.算学启蒙“总括”[M].郭书春.中国科学技术典籍通汇·数学卷(第一册).郑州:河南教育出版社,1993:1129.
[16]九章算术(卷二)[M].文渊阁四库全书.第797册.台北:商务印书馆,1983:21.
[17]九章算术(卷二)[M].文渊阁四库全书.第797册.台北:商务印书馆,1983:23.
[18][汉]张苍.九章算术[M].曾海龙,译.南京:江苏人民出版社,2011:36-37.
