双螺杆压缩机螺杆转子齿间容积内容积比的一种算法
2022-05-18管大渊
管大渊
(陕西汉机精密机械股份有限公司,陕西 汉中 723003)
1 引言
螺杆压缩机具有结构简单、零件数量少、体积小、故障率低等特点,具有宽广的容量和工况工作范围,近十年来在国内得到了较快的推广和应用。在双螺杆压缩机的设计计算工作中。螺杆转子齿间容积和内容积比是经常要用到的理论参数。齿间容积参数的准确度关联到压缩机容积流量参数的准确度,关联到压缩机内容积比参数的准确度,关联到压缩机的性能指标。邢子文教授在《螺杆压缩机——理论设计及应用》一书中给出了有关双螺杆转子齿间容积参数的计算公式。本文在该书的基本观点的基础上,结合工程实践,通过分析双螺杆压缩机螺杆转子工作基元的齿间面积与转子长度之间的关系,利用微积分工具,提出了一种工程设计中有关双螺杆转子齿间容积参数的计算方法,结合给定的内容积比可以计算并确定出气口的位置。
2 双螺杆转子,转角,螺距,齿间容积
双螺杆转子是双螺杆压缩机的核心零件。一对相互啮合的双螺杆转子具有螺旋升角相等、旋向相反、螺距相等以及共轭等基本特点[1]。
图1、图2和图4是根据给定的螺杆转子的型线数据、阴阳转子的齿数Z阴Z阳、阳转子导程T、转子长度L、中心距a参数,通过Solidworks软件生成三维实体图后转换得到的二维视图。
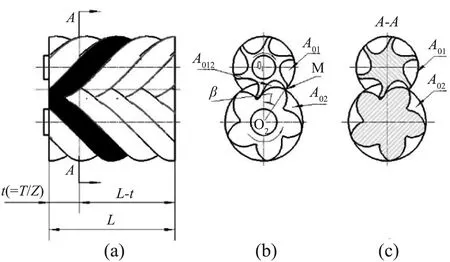
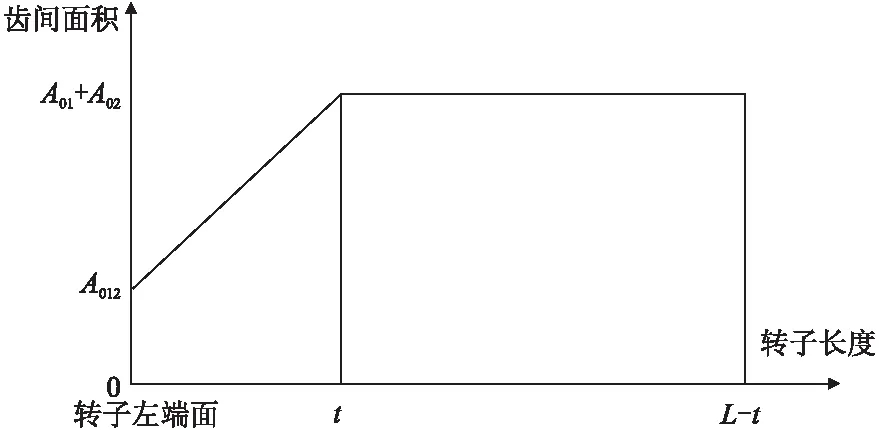
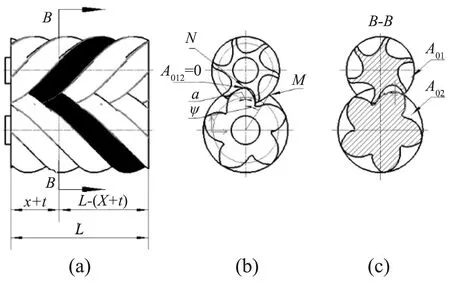
如图1,螺杆转子的端面齿形在端面圆上是等形状、等间隔分布的,齿数用Z表示。因此,相邻齿的间隔的角度(相位差)是2π/Z。导程T对应的转角是2π,螺距t=导程/齿数=T/Z,螺距t对应的转角是2π/Z。端面齿形(端面型线)的转动周期就是2π,在转动周期的轴向上的移动距离是导程T。显然,当转子齿形A的转角是2π/Z时,在转子的旋转方向的轴向前进方向上前进的距离就是t,A+i齿在转子的旋转方向的轴向前进方向上前进的距离就是it。当螺杆转子的A齿转动到相位角θ时,A+i齿在螺杆转子转角方向的轴向前进方向上,在it(螺距与齿数的乘积,0 图1 一对互相共轭啮合的阴阳螺杆转子,在端面上,当主动转子(阳转子)的A齿转动到相位角θ时,被动转子(阴转子)按照共轭关系与主动转子保持固定的相位关系(啮合);A+i齿在螺杆转子转角方向的轴向前进方向上,在it(螺距与齿数的乘积,0 下面主要分析压缩侧的工作基元齿间容积变化与转子长度变化之间的关系。 如图2所示,图2(b)是图2(a)的左视图,图2(c)是图2(a)的A-A剖视图(截面至端面距离t)。当阳转子转角为零度[1]时,阳转子齿顶点M与阳转子中心O2及阴阳转子中心连线O1O2的夹角为β,此时即将来到的压缩开始点阴转子齿间面积即将浸入阳转子齿间面积[1]该截面上工作基元的面积就是A01+A02;同时也注意到,正在进行的“A+1”工作基元(涂色腔)的齿间面积尚未完全关闭如图1(b)所示,此时的齿间面积为A012;通过前面的分析知道,从这个状态的端面向右1个螺距t的截面上(剖视图A-A),也存在一个与端面相同的阳转子转角为零度的旋转状态的截面,此时的阴转子齿间面积即将浸入阳转子齿间面积,这一截面上工作基元的面积也是A01+A02。如图1(c)所示,截面A-A与视图1(b)是重合的。在转子轴向长度t段内,“A+1”工作基元(涂色腔)的齿间面积由A012逐渐增大到A01+A02;在转子轴向长度t到L-t段内,“A+1”工作基元(涂色腔)的齿间面积为A01与A02不在相互浸入,齿间面积就是A01+A02。据此可以将“A+1”工作基元(涂色腔)的齿间面积的变化与转子轴向长度的变化关系可以用图3来表示。 图2 结合图3,此时的“A+1”工作基元(涂色腔)齿间面积与转子长度的变化关系,利用微积分计算体积的理论,可以列出“A+1”工作基元(涂色腔)齿间容积的计算公式: 图3 (1) 如图4所示,图4(b)是图4(a)的左视图,图4(c)是图4(a)的B-B剖视图(该截面至端面的距离是x+t)。 图4 当阳转子继续旋转,正在进行的“A+1”的工作基元(涂色腔)逐渐封闭,当阳转子齿顶M点转动到与阴转子相啮合的N点时,正在进行的“A+1”工作基元(涂色腔)完全封闭,此时在端面上的齿间面积A01+A02=0,该工作基元(涂色腔)吸气口完全封闭而压缩过程即将正式开始,所以这个状态时的“A+1”工作基元(涂色腔)的齿间容积就是理论最大齿间容积V吸。此时阳转子转过的角度是,阳转子转角零度转动到阳转子齿顶M和阴转子上共轭啮合点N时转过的角度ψ。设转角ψ对应的转子轴向上的移动量时x,则此时“A+1”工作基元(涂色腔)齿间面积为零时对应的转子长度的变化量就是x+t。螺杆转子的长度对应的扭转角是τ[1],τ=LT/360[1]。因此 x=ψ(L/τ) 式中τ——阳转子扭转角 夹角β和ψ可以运用理论型线有关数据进行计算得出也可基于CAXA工具直接在二维图形中直接量取。 很显然,当阳转子转角从零度转过ψ时,在轴向x+t截面处“A+1”工作基元(涂色腔)齿间面积最大,其值为A01+A02;在L-(x+t)长度上阴阳转子齿间面积A01与A02不在相互浸入,保持这一数值A01+A02;在左端面上由于正在进行的“A+1”工作基元(涂色腔)完全封闭,此时它在端面上的齿间面积A01+A02=0。因此这时这个“A+1”工作基元(涂色腔)齿间面积与转子长度的变化关系可以用图5来表示。 根据上面的分析,“A+1”工作基元(涂色腔)是理论最大工作基元,其容积就是齿间容积就是理论最大齿间容积。结合图5相邻工作基元(涂色腔)齿间面积与转子长度的变化关系,利用微积分可以列出“A+1”工作基元(涂色腔)齿间容积的计算公式 图5 =(A01+A02)[L-0.5(x+t)] (2) 式中A01——阴转子齿间面积 A02——阳转子齿间面积 L——转子长度 T——阳转子导程 t——转子螺距 τ——阳转子的扭转角 x——阳转子从转角零转到与阴转子共轭啮合位置时的转角ψ对应的阳转子轴向长度的变化量,x=ψL/τ 当阳转子继续转动,工作基元与出气口相通时,开始排气,如图6所示。此时,在这个基元内必然存在这样一个截面,其阴转子齿间面积即将浸入阳转子齿间面积,即阳转子齿顶上的M点转到了转角零度的状态,从该截面开始到排气端面,阴转子齿间面积不在浸入阳转子齿间面积而保持截面最大状态。假设,与出气口相通时的工作基元在至排气端面的距离为y时,阳转子齿顶上的M点转到了转角零度状态,故该工作基元此时的齿间面积为A01+A02,该截面到排气端面的距离就是y;根据前面的结论,从这一截面到A01+A02=0的截面的距离就是x+t。因此,可以得到工作基元与出气口相通时工作基元的容积V排的计算公式 图6 =(A01+A02)[0.5(x+t)+y] (3) ε=V吸/V排 ={(A01+A02)[L-0.5(x+t)]}/ {(A01+A02)[0.5(x+t)+y]} =[L-0.5(x+t)]/[0.5(x+t)+y] (4) (5) y为工作基元与排气口相通时,排气工作基元齿间面积最大截面至排气端面的距离。 公式(4)表明,内容积比ε只与螺杆转子的长度L、阳转子从转角零转到与阴转子共轭啮合位置时的转角ψ(工作基元最大吸气状态时)对应的阳转子轴向长度的变化量x、螺杆转子的螺距以及排气工作基元与排气口相通时,排气工作基元齿间面积最大时的截面至排气端面的距离y有关系,而与阴阳转子的齿间面积A01、A02没有关系。 参数y的计算结果,表明出气口位置的确定。 本文基于多头螺杆转角与螺距的变化关系,分析了螺杆转子齿间面积与螺距的变化关系以及螺杆转子齿间面积在转子长度上的变化关系,结合双螺杆转子的工作状态的分析,得出了双螺杆转子工作基元完全封闭状态下的最大理论齿间容积的计算公式。 根据给定的已知条件,齿间面积A01、A02可以基于CAXA软件的面积查询功能获得,阳转子的转角ψ是阳转子外圆上的点M转动到与阴转子相啮合的N点的角度,可以基于型线有关数据计算得出,此时就可以根据最大理论齿间容积V吸的公式计算双螺杆转子的最大理论齿间容积了。 内容积比只与螺杆转子的长度∠、吸气过程阳转子M齿顶点从转角零转到与阴转子共轭啮合位置N工作基元最大吸气状态时的转角ψ对应的阳转子轴向长度的变化量x、螺杆转子的螺距以及排气工作基元与排气口相通时,工作基元排气时齿间面积最大时的截面至排气端面的距离y有关系,而与阴阳转子齿间面积A01、A02没有关系。 计算出参数y,就确定了出气口的位置。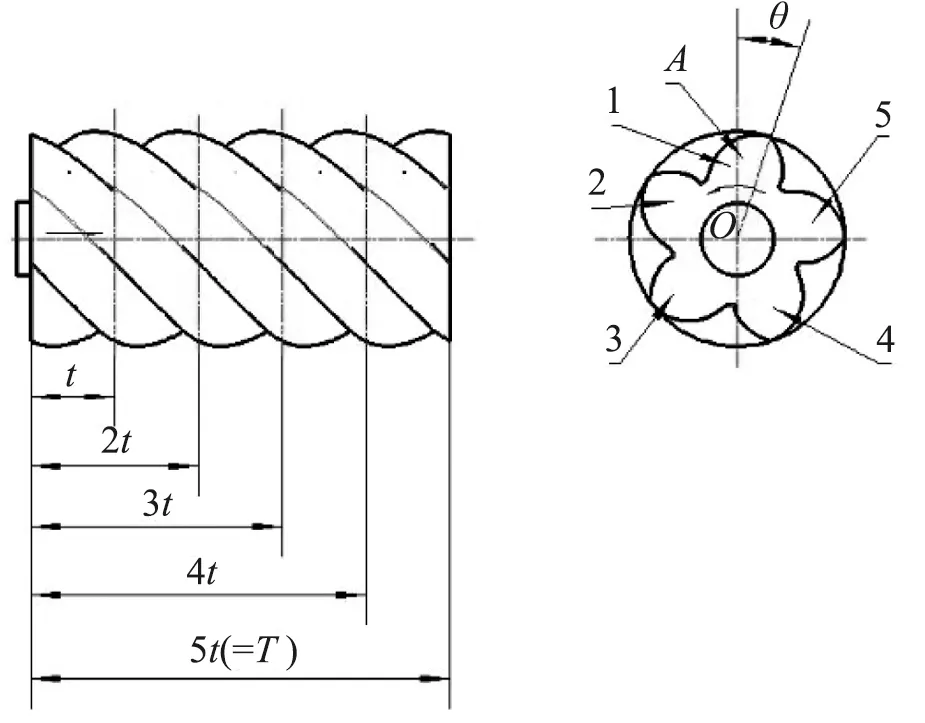

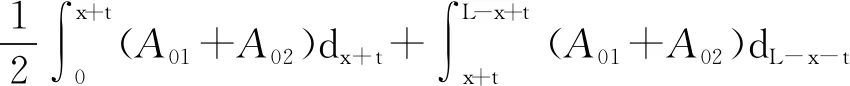
3 内容积比与出气口

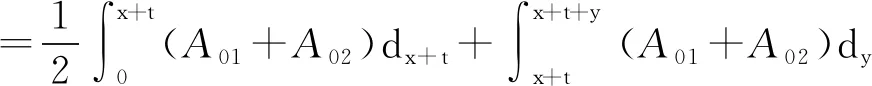
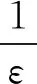
4 结论
