基于距离变化率的移动节点定位算法

张 楠，吴利刚

（山西大同大学机电工程学院，山西大同037003）

我们知道传统的无线传感网络定位中，信标节点都只能在一个限定的区域内移动，一般通过多次迭代，就能够提高定位精度。但是，在灾后救援的环境下，搜救设备一般需要在较大的范围内实施搜索，故传统的移动节点定位算法将不再适用。本文提出基于距离变化率的移动节点定位算法，很好地解决了上述问题。

1 定位方法

1.1 一个节点移动时定位

以传统的三边定位算法为基础，假设三个信标节点中有两个节点保持不动，而另外一个信标节点在较大范围内移动，在这种情况下，我们可以通过两个保持不动的节点，将定位区域缩小为两个点，此时寻找未知节点的任务就落在另外一个节点的身上，由其来完成，方法[1]如下：

设A、B两点所连直线为定位区域，C点为线段中点，CD为线段的垂直平分线，见图1。假如移动范围较大的那个信标节点与未知节点的距离为d(x)，那么d(x)会根据信标节点的移动而变化，其变化速率为ḋ(x)。

图1 信标节点位于垂直平分线上移动

如果信标节点由C点移动至点D，且移动方向刻未知节点和信标节点之间的距离为d(t)，在一个极小的时间Δt之后，两者之间的距离变化为d(t+Δt)，则认为为图1中所示，则信标节点与点A和点B的距离将会发生变化。

实际上，未知节点既可能位于A点，也有可能位于B点。当信标节点移动范围较大时，传感器可实时测量其与未知节点之间距离的变化，同时可以根据距离的变化来判断未知节点的位置。

本文中我们将ḋ()x进行如下定义：若某一时

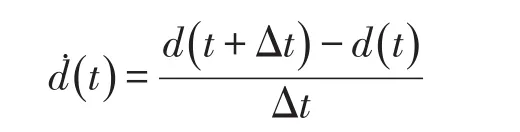
由图1可以看出，如果信标节点在D点的距离变化率小于0，我们就可以认为A点就是未知节点的位置；同理，如果距离变化率大于0，则B点即为未知节点的位置。

图1中所描述的情况只是一个特例，未知节点的可选位置有两个，信标节点在移动时，相对于点A和点B的距离变化率都是不同的，只要信标节点与未知节点的距离变化率与点A或点B的距离变化率一致，就可以将未知节点准确定位[2]。

1.2 两个节点移动时定位

在对未知节点进行定位的实施过程中，如果出现两个信标节点大范围移动，那么相对静止的信标节点就能够把未知节点的定位区域缩小在一个圆周上，然后在大范围移动的两个信标节点的帮助下，去除掉圆周上的无效区域，保留符合精度要求的位置信息[3]。

如果信标节点位于A点，那么定位区域就是一个圆，见图2。D点定位圆外的某一位置，箭头方向为其移动方向，B、C两点是与箭头垂直的虚线和圆的交点，E、F两点也在圆周上。

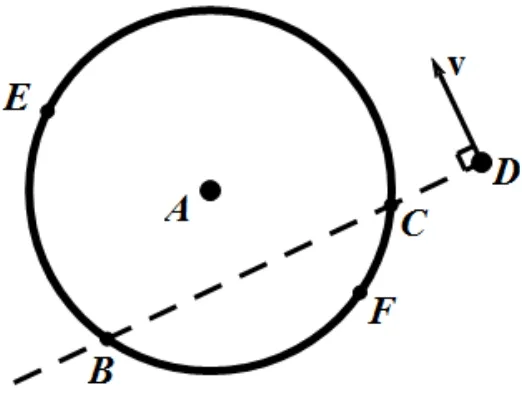
图2 距离变化率符号判别

如果信标节点作大范围移动，虚线就将圆切分为两个半圆。当信标节点的移动趋势就会变为靠近或远离即靠近某点的距离变化率符号为负，远离某点的距离变化率符号为正。我们通过利用这个特性，判断距离变化率，就可以知道信标节点是否正在接近未知节点，从而将未知节点定位[4]。

实际测量过程时，使用两个信标节点跟踪获取距离变化率，通过多次判断缩小定位区域，直到定位精度满足需求。

1.3 三个节点移动时定位

针对有三个信标节点移动的情况，我们可以将三者的移动范围视为定位区域，利用开始的几次距离变化，将定位区域限定在一个闭合区域，然后再多次判断，不断缩小限定区域，获得较高的定位精度[5-6]。

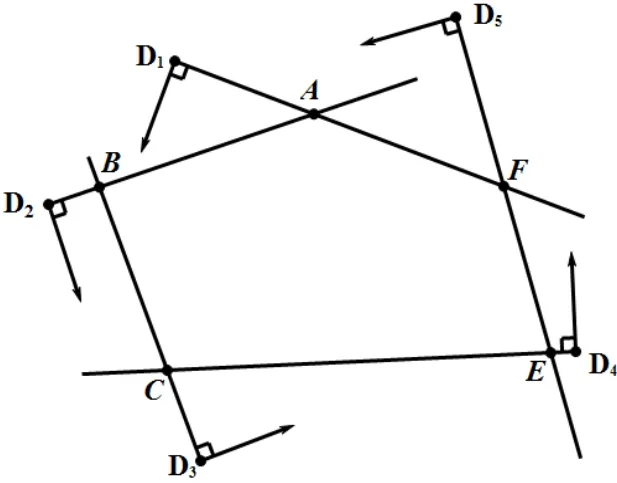
图3 封闭区域定位

通过分析5个有效节点距离变化，将定位区域限定在ABCEF范围之内，再通过多次使用该方法，逐渐缩小定位范围，直至满足定位精度，见图3。

2 算法仿真

2.1 一个节点移动时仿真

我们选择一个信标节点大范围移动的这种情况，对图1的所述情况进行仿真。设AC=BC=1，CD=3，假设开始时刻信标节点位于D点，之后沿BA方向匀速直线移动，则A点和点B之间的距离用以下公式表示：

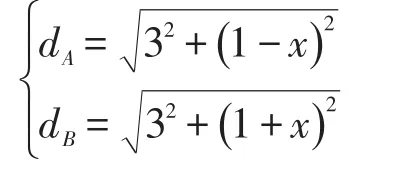
则A点和点B的距离变化率为：

从时刻0至1，信标节点相对于A、B两点的距离，见图4。

图4 信标节点相对于A、B两点之间的距离变化率

从图4中我们发现，ḋA≤0 ，而ḋB≥0 ，这样就可以很快获得未知节点的位置。

另外一种情况，当信标节点位于两参考节点连线的延长线上，见图5。

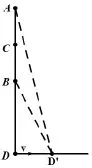
图5 信标节点在AB连线延长线上移动

设AB=BD=2，D点作为信标节点，其移动轨迹是沿AB垂直方向做直线移动，则A、B两点之间的距离可以用以下公式表示：

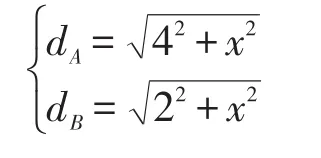
则相对于A、B两点的距离变化率为：

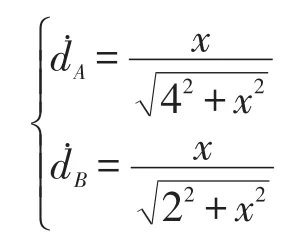
从时刻0至1，信标节点相对于两参考节点的距离变化率，见图6。由于信标节点是远离A、B两点移动的，所以相对于这两点的距离变化率符号均为正，但信标节点相对于点A的距离变化率始终要比信标节点相对于点B的距离变化率要小。因此，在实际应用中，也可以用此办法来确定未知节点的位置。

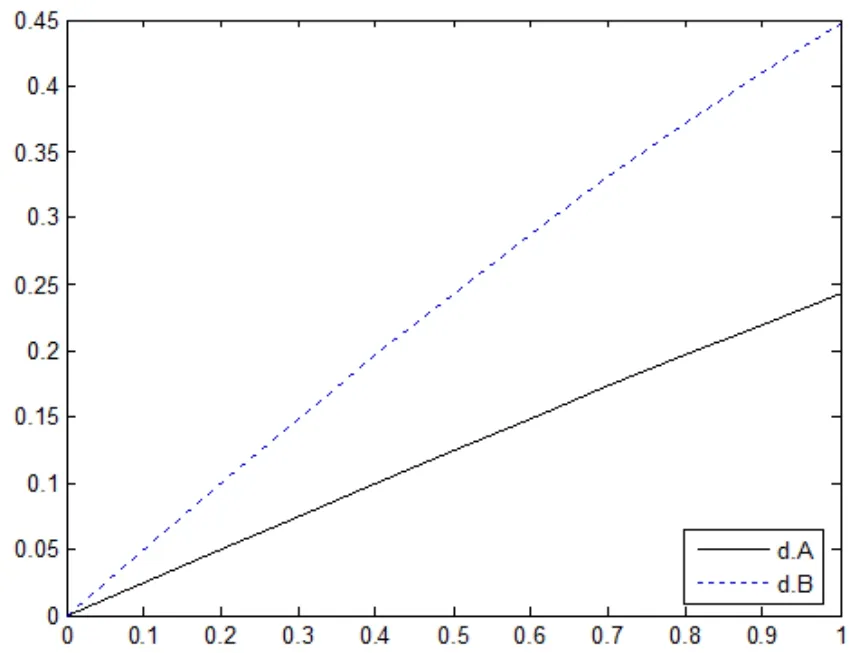
图6 信标节点在AB连线延长线上时距离变化率

2.2 两个节点移动时仿真

针对两个信标节点移动的情况，⊙A依然为为定位圆，未知节点R位于圆周上。我们按照上述方法，判断移动方向和距离变化率之间的关系，获取未知节点位于的位置。

我们假设信标节点可能的50个位置，随机给出移动方向，并保留距离变化率正负分界线，见图7。

图7 两个节点移动时50个样本的定位

通过去除无效节点，未知节点定位的区域一目了然，即两条虚线与⊙A相交形成的扇形区域，见图8。

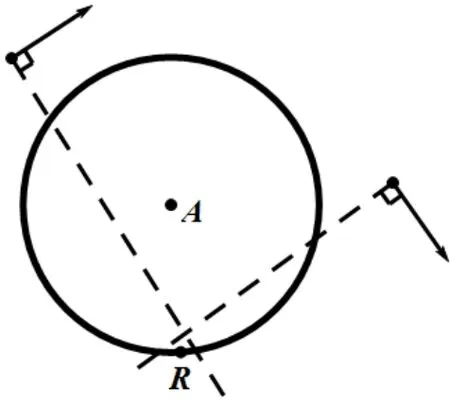
图8 去除无效节点后50个样本的定位

经测量知道，该段弧长的所对应的圆心角为13.83°，相比于一个信标节点定位的情况，精度提高26倍之多。

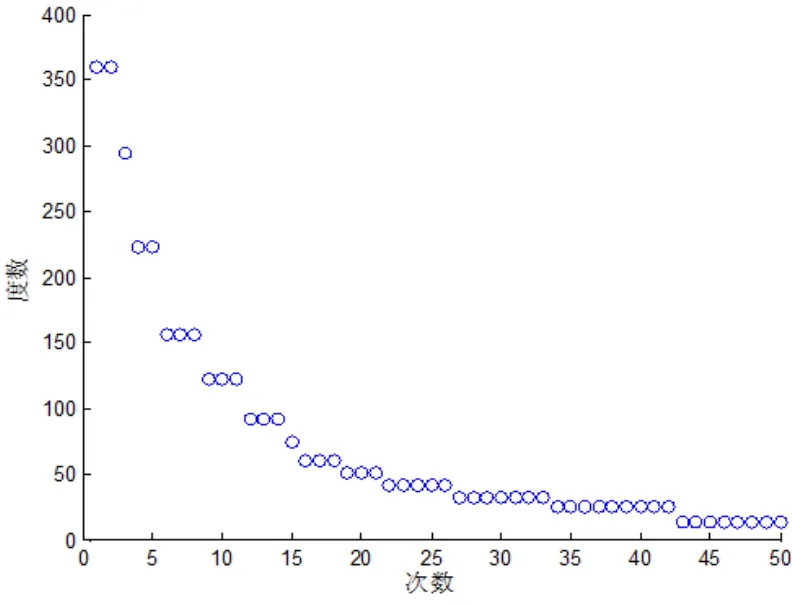
图9 两个节点移动时50个样本的定位过程

图9表明了样本个数和定位精度之间的关系。定位开始时，定位范围可看作一个圆，之后每缩小一次定位范围，记录定位弧长所对应的圆心角度数，以此表示定位范围的变化，即13.83°圆心角所对应的弧长就是我们所要确定的定位区域。如需要进一步提高定位精度，可依此办法多次迭代，最终达到预期精度即可。

2.3 三个节点移动时仿真

当三个信标节点移动时，我们给出初始定位区域，这次依然选取50个信标节点作样本，经过分析50次距离变化率得到定位结果，见图10。

图10 三个信标节点移动时50个样本的定位

图11 三个信标节点移动时前50个样本的定位过程

具体的定位过程，见图11。初始的定位区域是一个面积为37.82的五边，定位之后的区域面积为1.75，仅为开始时的4.6%，所以基于距离变化率的定位效果已经很明显。

3 结语

基于距离变化率的定位算法在实际应用中实现起来比较简单，定位效果也比较明显，只是在获取信标节点与未知节点之间距离的过程中，环境、数据延时等因素会影响定位精度。因此，在定位精度要求较高的应用过程中，最好能够和其他定位算法配合使用。

[1]陈星舟.无线传感器网络定位算法研究[D].厦门:厦门大学，2011.

[2]滕国栋.无线传感网络节点定位算法的研究[D].杭州:浙江大学，2010.

[3]罗卿.无线传感器网络中的栅栏覆盖研究[D].长沙:湖南大学，2012．

[4]欧爱军.无线传感网络覆盖及路由研究[D].上海:东华大学，2013．

[5]杨泽军,王英龙,黄太波.基于APIT的无线传感器网络三维定位算法[J].单片机与嵌入式系统应用,2012,12(5):5-8.

[6]彭力,张炜.基于循环求精的APIT无线传感器网络定位算法[C]∕∕第29届中国控制会议.2010.