矩阵等价与相似和合同的判断

张慧芬

（山西大同大学数学与计算机科学学院，山西大同 037009）

1 概念描述

等价设A与B为m×n矩阵，存在可逆矩阵P，Q，使得PAQ=B，则称A与B等价。

相似设A与B为n×n矩阵，存在可逆矩阵P，使得P-1AP=B，则称A与B相似。

合同设A与B为n×n矩阵，存在可逆矩阵P，使得PTAP=B，则称A与B合同。[1-3]

2 区别与联系

（1）等价只要求矩阵A与B是同型矩阵，不一定是方阵，但相似和合同要求矩阵A与B必须是同型矩阵中的方阵。

（2）矩阵的等价、相似、合同实际都是矩阵之间的初等变换，只不过变换方式不一样。

说明如下：

由可逆的充要条件，A可逆⇔A=P1,P2,…,PS,且P1,P2,…,PS是初等矩阵。

故等价的PAQ=B，即存在m阶初等矩阵P1,P2,…,PS和n阶初等矩阵Q1,Q2,…,Qt，使得

PS,…,P2P1AQ1Q2,…,Qt=B；

相似的P-1AP=B，即存在n阶初等矩阵P1,P2,…,PS，使得

合同的PTAP=B，等价是即存在n阶初等矩阵P1,P2,…,PS，使得

三者都是相当于对A任意做有限次初等行变换和初等列变换。但是相似和合同作初等行变换和列变换的次数是一样的，相似做一次列变换，再作一次相应的逆行变换，合同做一次列变换，对应的作一次同样的行变换。

3 判别

在判别矩阵的三种关系是，秩是等价关系的不变量，而相似和合同也是等价的，秩也不变，再结合特征值和正负惯性指数来区别相似和合同,注意合同仅限于对称阵。

（1）矩阵A与B等价⇔R(A)=R(B)；

（2）可以借助一些必要条件来判定矩阵不相似:

若A与B相似⇒A与B有相同的特征值；

⇒A与B有相同的迹；

⇒|A|=|B|。

但如果以上的必要性成立，不再能说明矩阵的相似，这时一般利用取其重特征值时构成的矩阵的秩，即R(A-λE)来进一步判定。

（3）对于实对称矩阵，有一些可以直接用的结论：

①实对称矩阵A与B相似⇔A与B具有相同的特征值；

证明A与B相似，即存在可逆矩阵P，使得P-1AP=B。故|

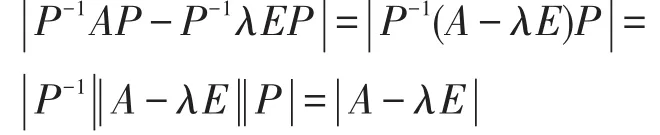
可知特征值相同。

实对称矩阵A与B有相同的特征值，存在正交矩阵使得A与B一定相似于相同的对角阵，由相似关系的传递性知，A与B相似。

证毕

②实对称矩阵A与B合同⇔二次型xTAx与xTBx具有相同正负惯性指数；

证明A与B合同，即存在可逆矩阵P，使得PTAP=B。由于B是实对称矩阵，故一定存在正交矩阵Q，使得

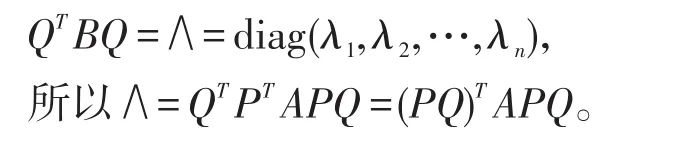
即A与B都合同于对角阵∧。

可知二次型xTAx与xTBx具有相同正负惯性指数。

二次型xTAx与xTBx具有相同正负惯性指数，一定存在可逆的线性变换x=Py与y=Qz，使得

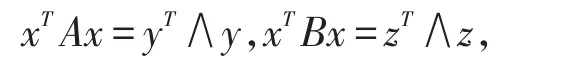
所以A与B都合同于∧，由合同的传递性知A与B合同。

证毕

③实对称矩阵A与B相似⇒A与B合同。

证明实对称矩阵A与B相似，A与B具有相同的特征值，即存在正交矩阵P,Q，使得

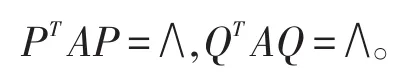
从而

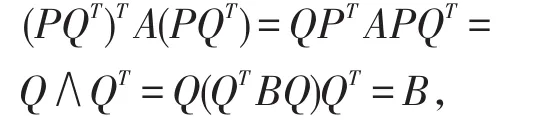
故A与B合同。

4 举例

例1判定下列矩阵哪些等价、相似、合同,

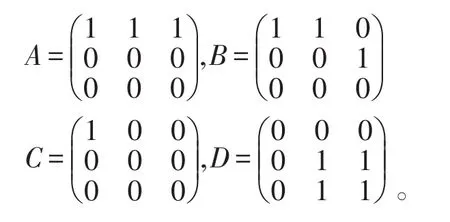
解R(A)=R(C)=R(D)=1,R(B)=2。

所以A,C,D等价。

由R(B)=2≠1可以看出相似排除B，A,C的特征值是1,0,0。D的特征值是2,0,0。可以看出相似排除D。取二重特征值0时，3-R(A-λE)=3-R(A)=2,有两个线性无关的特征向量，A可相似对角化，A与C相似。

合同只限于实对称矩阵，观察C,D的特征值。C，D的正惯性指数都为1，负惯性指数都为0，由②得C,D合同。

例2已知矩阵

则（）

(A)A与C相似，B与C相似

(B)A与C相似，B与C不相似

(C)A与C不相似，B与C相似

(D)A与C不相似，B与C不相似

解可求出A,B,C的特征值都是2,2,0，且A,C都是实对称矩阵，由①得A与C相似。对于矩阵B,3-R(B-2E)=3-2=1，只有一个特征向量，B不可相似对角化，B与C不相似。所以选(B)。

[1]高志强,庞彦军.线性代数[M].北京：科学出版社,2016.

[2]智婕.矩阵等价、相似、合同的联系[J].牡丹江师范学院学报，2011,76(3):2-3.

[3]蒋卫华,王洪滨.线性代数教学中两组概念的处理[J].大学数学，2005,21(1):120-123.