分子间的吸引相互作用对实际气体等温线的影响

闫世平,康占成

（1.忻州师范学院物理系，山西忻州034000;2.山西大同大学物理与电子科学学院，山西大同037009）

在热力学理论中，可查内容多为范德瓦耳斯方程来对气液相变问题进行分析和实验，范德瓦耳斯方程只能够对理想气体进行解释，能够将理想气体模型当中没有涉及到的气体分子大小以及相互作用力进行分析，可以更好的对宏观物理性质进行分解。[1,2]但是方程具有一定的局限性，其方程只表示了在密度较低时分子的作用情况，其中引力项所代表的参数a在描述气液相变时和实验结果有一定差异。[3-6]所以需要将体积和分子吸引相互作用带入到范德瓦耳斯方程当中，对其作出一定的改进，能够更加全面的显示出分子间吸引相互作用为气体等温线带来的影响。

1 分子间的吸引相互作用

物理学界将分子间作用分为排斥作用以及吸引作用两种，在正常条件下，两个分子间既存在排斥作用，也同样存在吸引作用，最终所形成的作用或者反应便是两者之和。对分子的作用进行分析，又可以将重新定义为长程作用和短程作用。[2]长程作用当中包括静电作用、诱导作用、色散作用。若分子间的距离较小，那么其电子云会出现叠加，随即发生排斥反应，排斥反应会随着指数数值变化而减小，可以将其称之为短程反应。从理论上进行分析，可以根据量子力学当中原理进行计算和实验。

1.1 静电作用

分子和离子能够组成流体混合物，离子本身具有正电荷和负电荷两种形态，分子成球形所产生的气体是惰性气体，并且在电荷分布上与球对称，其中正电荷与负电荷在中心点位置发生重合，可以命名为非极性因子。若分子的正负电荷中心没有产生重合反应，则称之为为极性分子，形成偶极矩。这其中的分子所呈现的属性不同，一部分带有多个正或负的电荷中心，并且可以组建成四偶极矩、八偶极矩或者其他的形式的偶极矩。这些离子或者偶极分子在相互作用时能够产生静电作用。

1.2 弱化学作用

分子间运动发生物理作用之外还会发生一些具有饱和性以及方向性的弱化学作用，这种作用主要起源于分子间的氢键发生了电荷转移效果。[2,6-8]

在价键理论当中，若价键原子排列方式不同，共享的电子则会受到吸力更强的原子吸引，发生电负性反应。化合物中含有氢元素的较多，比如：o-H、-H、X-H或者强吸电子基团C-H等，氢原子周围电子云会根据吸引力发生反应，其中一部分氢原子会与O、N、F、S这些孤立电子或者原子发生化学反应，并形成A-H…B方式的弱化学键，氢键则是弱化学键。

不同种类分子间形成的氢键能够产生特殊的反应。这种反应发生在质子受体物质或者其他质子受体之间。比如乙醇与水发生的反应、乙醇和氯仿发生的反应或者乙醇和丙酮发生的反应，这些反应都是溶剂化反应。[9,10]

1.3 色散作用

Ar、CH4等非极性物质当中没有偶极矩和多极矩，但是可以在一定的环境下发生液化反应，这种反应能够显示出两个非极性分子具有一定的吸引力。主要是由于分子间正负电荷在重合的一瞬间，产生了瞬间偶极反应，所以周期性在一定程度上产生了变化，经统计的平均数是0。两个分子发生诱导偶极反应之后产生了吸引力。

1.4 憎水作用

分子间反应主要发生在液体混合间，在同一种分子间发生反应时被破坏，最后形成了一种异种分子间的作用。若异种分子间产生的吸引力较同种分子间更弱，那么在混合的过程当中，破坏作用则需要释放更大的能量才能保障分子间作用抵消。△mixH（=HE）在这个反应当中混合过程产生吸热作用。若异种分子间吸引力持续增加，那么△mixH则是负值，从而产生放热反应。若少量的氢在溶解过程中没有断裂而是发生了变形，那么溶解速度会增加，水中所含的分子重新排列，系统当中的熵下降，熵的损失使溶解速度变慢，产生憎水反应。

2 范德瓦耳斯方程及等温线计算

2.1 范德瓦耳斯方程

自1850年以后，分子相互运动理论研究逐渐演变成一门学科，此学科具有高度精密性特征。经过对分子运动的不断研究，人们慢慢发现实验当中大多数气体产生的运动与理想气体的形式不相符。曾有学者在十九世纪中期之前就已经发现除了氢气之外的气体都没有形成理想气体定律，经过多年的研究焦耳与W.汤姆逊用实验对分子作用进行了证实，研究者安德鲁斯通过实验验证了二氧化碳在环境不同的条件下等温线的变化，产生临街点。后续研究者范德瓦耳斯研究出范德瓦耳斯方程，解释了安德鲁斯的研究，其方程式为

2.2 范德瓦耳斯方程等温线公式表述

将1 mol气体作为研究对象，范德瓦耳斯方程的计算形式为：

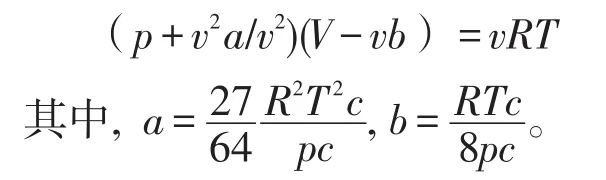
在此公式中Tc，Pc代表的是临界温度以及临界压强。

图1 范式方程等温线变化曲线

从图1当中可以看出，T在取不同的数值时，二氧化碳气体范德瓦耳斯方程的等温线变化，在实验过程中，二氧化碳气体的临界值Tc=304.19 K,Pc=73.80*105Pa，Vc=94.01*10-6m⋅mol-1,。在此途中可以发现，T=250 K的等温线当中，其中一部分曲线压强＜0，也可以说成是当T＜T0时，范德瓦耳斯等温线曲线变化当中存在一段p＜0的曲线，并且出现温度点数值较小，能够满足P=0。

气体不同则T0不同，对于二氧化碳在气体当中的变化可以进行计算，T0=256.7 K，则会高于二氧化碳气体正常汽化点温度194.6 K。

图2 范德瓦耳斯方程排斥项和吸引项间的关系

3 范德瓦耳斯方程的修正方式规划

分子之间的相互吸引作用和温度、密度有一定关联，因此，在计算时不能够将引力项a设置为常数。

3.1 波塞洛特方程

波塞洛特方程在引力项当中加入了温度因子，以1摩尔气体作为研究对象，所表达的方程是：

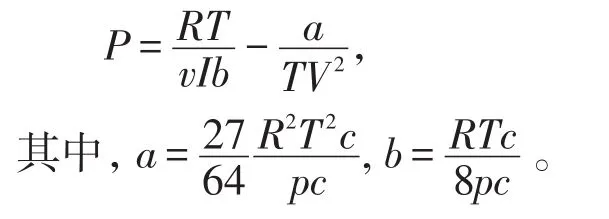
3.2 克劳修斯方程

克劳修斯方程既引入了温度与吸引项的关系，又对吸引项和比容函数的关系进行了分析，1mol气体的克劳修斯方程为：

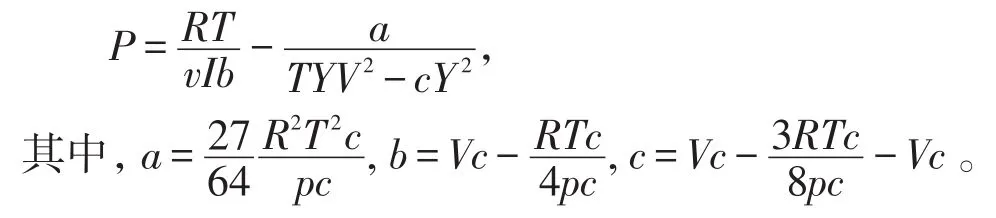
4 结论

(1)通过图3可以发现，3种方程在T=294.5K时的等温线变化，其中●线、○线、□线，代表了上述三种方程，第一种为范式方程、第二种为波塞洛特方程、第三种为克劳修斯方程。在应用这些方程进行研究气液相变时，等温线形状和距离基本相似，并且都有一段曲线。

(3)对比三种方程方式可以看出，克劳修斯方程在相同温度依赖关系方面比波塞洛特方程在比容函数形式上进行了一定的改进。从图3中也可以发现克劳修斯等温线与波塞洛特等温线基本一致，只是发生了一定程度的平移，因此，最终比容函数形式向左发生了一定的偏移。

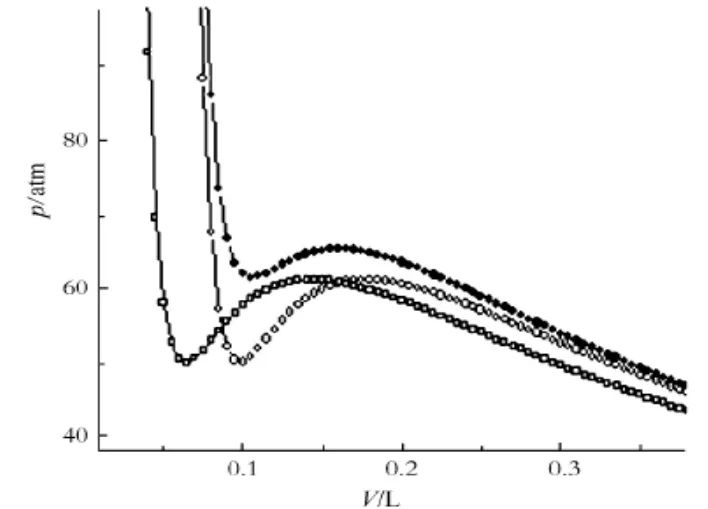
图3 三种方程的等温线

结合实际来看，以上三种方程形式描述等温线气液相变上依旧存在一定的问题，并且问题基本一致，这也是方程本身存在的局限性决定的，三种方程没有在本质上对范德瓦耳斯方程进行改变，所以，在T∕P不变的条件下，方程都能够将V看作是三次方，并且方程中吸引项对温度的依赖性比较简单，排斥项和吸引项所产生的变化规律，不能对实际等温线气液共存的问题进行详细描述。

[1]张盼盼.对双酚A分子印迹体系分子间氢键相互作用的理论研究[D].长春：吉林大学,2017.

[2]焦放.基于原子力显微镜研究（模拟）生物分子相互作用与行为机理[D].上海：华东师范大学,2016.

[3]张永梅.实际气体分子间吸引相互作用对转换温度的影响[J].物理通报,2015(01):20-22.

[4]章建东.分子间相互作用势能面的高精度从头计算与应用[D].苏州：苏州大学,2014.

[5]赵东波.分子酸性、顺式效应和锌指蛋白金属键合特异性的密度泛函活性理论研究[D].长沙：湖南师范大学,2013.

[6]张永梅.分子间的吸引相互作用在处理实际气体行为中的影响[J].物理与工程,2012,22(05):12-13，29.

[7]李波.基于氰根、邻菲罗啉、8-羟基喹啉或磷酸根的零、一或三维分子磁体的结构与磁性行为之间相互关系的研究[D].长春：东北师范大学,2015.

[8]周盼盼.分子间弱相互作用体系的理论研究：氢键、范德华相互作用和卤键[D].兰州:兰州大学,2012.

[9]汪朝旭,刘和秀,郑柏树,等.氯代乙炔HCCCl与卤代乙炔HCCR(R=Cl,Br)分子间相互作用的理论研究[J].湖南科技大学学报(自然科学版),2015,25(01):94-97.

[10]王菊.主客体分子体系：环己烷及其衍生物包结于分子反应器内的理论研究[D].北京:北京化工大学,2012.