透视中考试题中“点的坐标”
2018-04-25曹玲玲
曹玲玲
“点的坐标”内容虽然不多,但涉及的问题却不少,它是函数和几何图形类问题研究的基础,也是整个“数学大厦”的基石,所以我们在学习这部分内容时,只有准确把握四个象限内和坐标轴上点的坐标特征,领会图形变换与坐标的关系,理解坐标的意义,才能做到有的放矢,从容应对.下面仅以2017年中考试题为例予以分析,希望对大家的学习有所帮助.
考点1 探寻点的特征
例1 (2017·贵港)在平面直角坐标系中,点P(m-3,4-2m)不可能在( ).
A.第一象限 B.第二象限
C.第三象限 D.第四象限
【分析】本题没有正面考查点在第几象限,而是反过来问不可能在第几象限,命题者有意考查同学们逆向思维的能力和分类讨论的意识,在解题思路上我们可以考虑先确定点P的横坐标的符号,再分析点P的纵坐标的符号,从而确定该点所在的象限.
【解答】①当m-3>0,即m>3时,4-2m<-2,所以点P(m-3,4-2m)在第四象限;②当m-3<0,即m<3时,4-2m>-2,所以点P(m-3,4-2m)可以在第二或第三象限.综上所述,点P不可能在第一象限,故选A.
【点评】本题重点渗透了分类讨论的思想,在处理该问题时我们应思考,m-3和4-2m能同时为正吗?可能同时为负或一正一负吗?具体可分类列出下面四个不等式组:
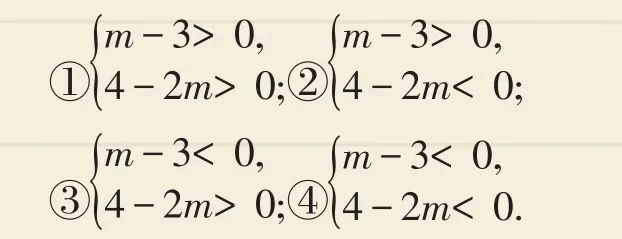
然后我们观察哪组不等式组无解即可.另外,作为选择题还可以用特殊值法,分别取一些m的值代入进行验证.
考点2 确定点的坐标
例2 (2017·常州)如图1,已知矩形ABCD的顶点A、D分别坐落在x轴、y轴上,OD=2OA=6,AD∶AB=3∶1,则点C的坐标是( ).
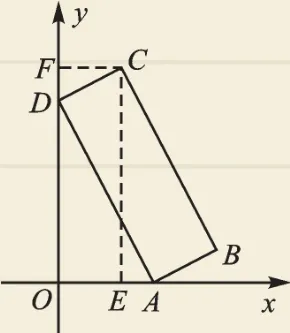
图1
A.(2,7)B.(3,7)C.(3,8)D.(4,8)
【分析】本题以矩形为载体,考查矩形性质的运用,解题的关键是将AD∶AB转化为AD∶DC,再运用相似将其转化为△OAD与△FDC的相似比(如图1),进而通过比求出CF和DF的长,最终得到点C的坐标.
【解答】过点C分别作CE⊥x轴、CF⊥y轴,垂足分别为E、F,由题意可得:
△CFD∽△DOA,
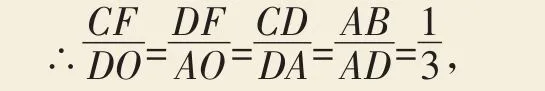
∵OD=2OA=6,∴CF=2,DF=1,
∴CE=OF=OD+DF=7,
故点C的坐标为(2,7).
【点评】同学们在解决此类问题时先要结合条件搞清楚图形的特征,抓住基本模型——“一线三等角”(∠DOA=∠ADC=∠CFD=90°),找出相似三角形,运用相似比解决问题.
考点3 变换点的位置
例3 (2017·无锡)操作:“如图2,P是平面直角坐标系中一点(x轴上的点除外),过点P作PC⊥x轴于点C,点C绕点P逆时针旋转60°得到点Q.”我们将此由点P得到点Q的操作称为点的T变换,则点P(a,b)经过T变换后得到点Q的坐标为______,点M经过T变换后得到点N(6,-3),则点M的坐标为____.
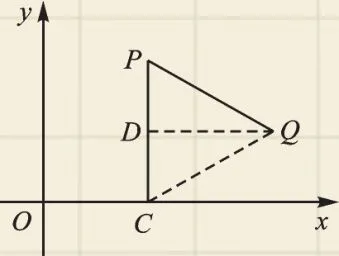
图2
【分析】本题实质上是通过旋转变换考查等边三角形的性质,形成变换前的点与变换后的点之间的对应关系,在找到这个对应关系的基础上运用方程解决问题.
【解答】如图2,连接CQ,过点Q作QD⊥PC于点D,由旋转可知△PCQ为等边三角形.
∵P(a,b),∴OC=a,PC=b,
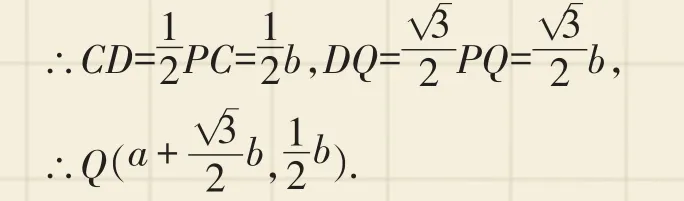
事实上,不论P(a,b)在第几象限,变换后的点Q的坐标始终为Q()[注:可分P在x轴上方、P在x轴下方两种情况讨论],故设M(x,y),则N(

【点评】解决旋转变换类问题的关键是抓住旋转的角度和旋转前后的不变性,结合图形的特征解决问题.
由于“点的坐标”这部分知识容易与其他知识相融合,近几年来,中考试题对其考查的力度不断加大,尤其是结合平面几何的相关知识,希望大家在思想上能给予足够的重视.
考点4 探索点的规律
例4 (2017·黔东南)把多块大小不同的30°直角三角板按如图3所示摆放在平面直角坐标系中,第一块三角板AOB的一条直角边与y轴重合且点A的坐标为(0,1),∠ABO=30°;第二块三角板的斜边BB1与第一块三角板的斜边AB垂直且交y轴于点B1;第三块三角板的斜边B1B2与第二块三角板的斜边BB1垂直且交x轴于点B2;第四块三角板的斜边B2B3与第三块三角板的斜边B1B2垂直且交y轴于点B3;……按此规律继续下去,则点B2017的坐标为______.
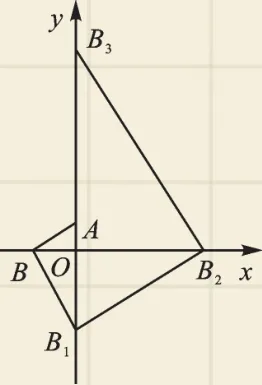
图3
【分析】观察图形,寻找图形的变化规律,在依次求出点B,B1,B2,B3坐标的基础上,结合B到B4,依次由x轴负半轴、y轴负半轴、x轴正半轴、y轴正半轴,再回到x轴负半轴,经过排队观察总结出其变化的规律后,根据规律去猜想点B2017的坐标.

∴OB2017=(2018=31009,
又∵2017÷4=504……1,
∴点B2017在y轴负半轴上,
∴点B2017的坐标为(0,-31009).
【点评】解决此类问题的关键在于学会观察图形变化的规律,这里有两个变化的规律,一是OBn的长度随着n的变化而变化,二是点Bn的位置在旋转中发生变化,结合这两个变化的规律,先表示出线段OB2017的长,再确定点B2017的位置,从而解决相关问题.
