吃一堑长一智
2018-04-25徐永军
徐永军

易错点1:未分类思考
例1 若一个点到圆上的点的最小距离为4cm,最大距离为10cm,则该圆的半径是____cm.
【错解】7cm.
【正解】3cm或7cm.
【错解辨析】有两种情况:(1)当此点在圆内时,如图1所示,半径OB=(PA+PB)÷2=7;(2)当此点在圆外时,如图2所示,半径OB=(PB-PA)÷2=3.故该圆的半径为3cm或7cm.所以求解点与圆位置关系时要注意分类讨论思想的运用.
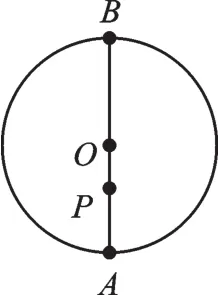
图1
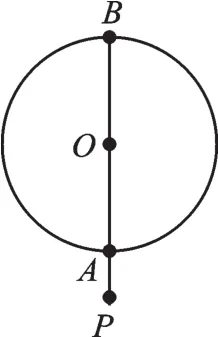
图2
例2 已知半圆O的半径为R,M为其直径AB上一点,过点M作PM⊥AB交半圆于点P,且,则AM=_______.
【错解辨析】本题没有图,所以要注意点M在半径OA上和在半径OB上的两种情形:(1)点M在圆心O与点A之间(如图3所示);(2)点M在圆心O与点B之间(如图4所示).
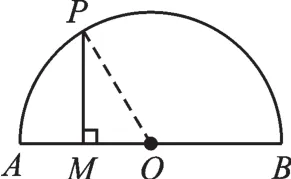
图3
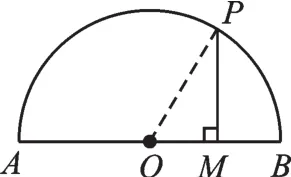
图4
易错点2:对题意理解不清
例3 如图5,已知⊙O的直径为10,点P是⊙O内一点,且OP=3,则过点P且长度为整数的弦的条数是( ).
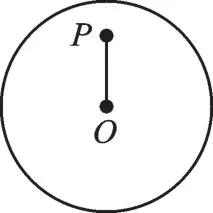
图5
A.1 B.2 C.3 D.4
【错解】C.
【正解】D.
【错解辨析】过点P且与OP垂直的弦的长度为8,它是最短的弦,只有一条;过点P的直径是最长的弦,长度为10,只有1条;过点P且长度为9的弦有2条.这样过点P且长度为整数的弦共有4条.错解的原因在于可能漏掉了最短的弦或最长的弦(直径).
易错点3:考虑问题不全面
例4 平面上的A、B、C三点,若经过这三点作圆,则作出的圆有( ).
A.0个 B.1个 C.1个或0个 D.无数个
【错解】B.
【正解】C.
【错解辨析】由于三点可能在同一条直线上,也有可能不在同一条直线上,因此需要分情况加以讨论,即作出的圆有1个或0个.
例5 已知⊙O的直径为6,P为直线l上一点,OP=3,那么直线l与⊙O的位置关系为________.
【错解】相切.
【正解】相交或相切.
【错解辨析】错因:误将OP长当成距离.如图6所示,d=r;如图7所示,d<r.直线与圆相切是指圆心到直线的距离等于半径,这里OP=3并不一定是圆心O到直线l的距离.
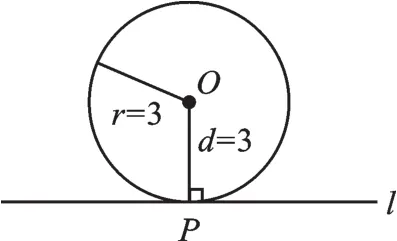
图6
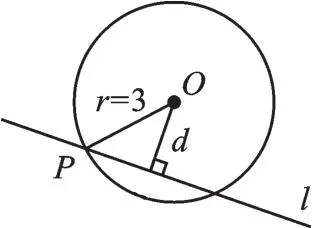
图7
易错点4:不能准确根据圆的半径确定符合条件的圆的个数
例6 已知点A、B,经过A、B两点作圆,则半径为2cm的圆有_______个.
【错解】2个.
【正解】2个、1个或0个.
【错解辨析】本题应分为三种情况:(1)如图8所示,当AB<4cm时,能作2个圆,圆心在AB的垂直平分线上;(2)如图9所示,当AB=4cm时,只能作出一个圆,圆心为AB中点,AB为直径;(3)当AB>4cm时,不能作圆.
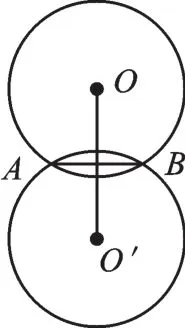
图8
图9
易错点5:对画图时的多种情况掌握不熟,从而丢解
例7 已知点O是钝角三角形ABC外接圆的圆心,则∠A与∠BOC的数量关系为____ .
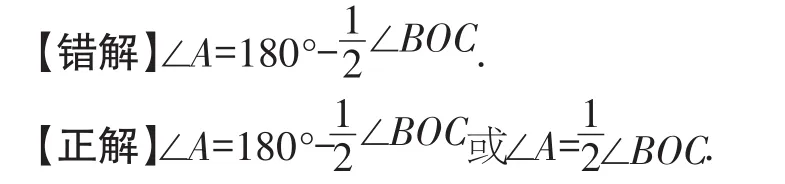
【错解辨析】错解未弄清楚哪个角是钝角,如图 10所示,当∠A为钝角时,∠A=180°-OC.若∠ABC(或∠ACB)为钝角,如图11所示,BOC.解答此题的关键是把所有符合题意的图形画出来.

图10
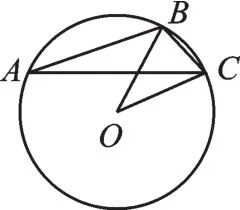
图11
易错点6:求圆周角的度数时易丢解
例8 已知⊙O的半径为2,A、B、C为⊙O上的三点,且BC=23,求∠A的度数.
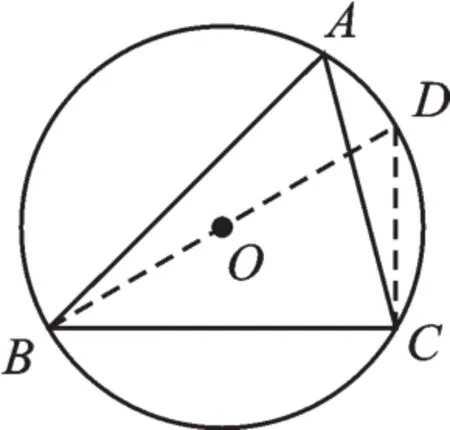
图12
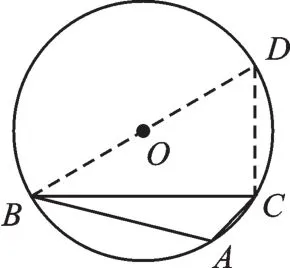
图13
【错解】如图12所示,连接BO并延长交⊙O于点D,连接CD,则BD=4.
∵BD是⊙O的直径,
∴∠BCD=90°,
又∵BC=23,
∴∠D=60°,∴∠A=60°.
【正解】分两种情况讨论.(1)当点A在BC所对的优弧上时,如图12所示,连接BO并延长交⊙O于点D,连接CD,则BD=4.
∵BD是⊙O的直径,∴∠BCD=90°,
又∵BC=23,
∴∠D=60°,∴∠A=60°.
(2)当点A在BC所对的劣弧上时,如图13所示,连接BO并延长交⊙O于点D,连接CD,则BD=4.
∵BD是⊙O的直径,∴∠BCD=90°,
又∵BC=23,
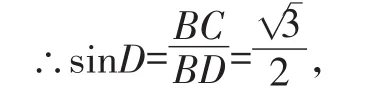
∴∠D=60°,
∴∠A=120°.
综合(1)(2)得∠A的度数为60°或120°.
【错解辨析】很多同学只考虑了点A在BC所对的优弧上的情况,忽略了点A还有可能在弦BC所对的劣弧上.在同圆中,当一条弦所对的两个圆周角在弦同侧时,它们相等,在弦异侧时,它们互补.
易错点7:错用弧、弦之间的关系
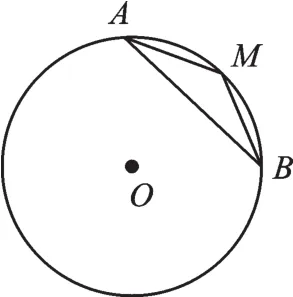
图14
A.AB>2AM
B.AB=2AM
C.AB<2AM
D.AB与2AM的大小关系不能确定
【错解】B.
【正解】C.
【错解辨析】在⁀各选项中,AB与AM均指的是弦长,而“M为的中点”指的是弧的数量关系,两者不能一概而论.⁀
又∵AM+BM>AB,
∴2AM>AB,即AB<2AM.
易错点8:忽视圆心与角的位置关系
例10 已知AB是⊙O内接正方形的一边,AC是⊙O内接正三角形的一边,则∠BAC=_______.
【错解】75°.
【正解】75°或15°.
【错解辨析】错解只考虑了圆心在∠BAC内部的情形,如图15所示,连接OA,OB,OC,因为AC、AB分别为⊙O内接正三角形和内接正方形的边,所以∠AOC=120°,∠AOB=90°,此时∠CAO=∠ACO=30°,∠OAB=∠OBA=45°,所以∠CAB=75°.而当圆心在∠CAB外部时,如图16所示,连接OA,OB,OC,则∠CAB=15°.解决此题的关键是弄清图形的不同情况,再利用正多边形的有关知识进行求解.
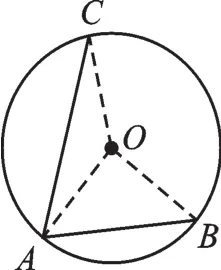
图15
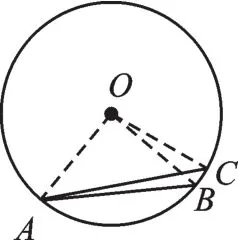
图16
“圆”的学习过程中要注意对概念的辨析,加深对图形的认识,考虑问题一定要全面细致.以上是对同学们在解决圆有关问题时容易出错的环节的一些总结和思考,希望能为同学们的学习提供参考.
