基于Mindlin理论的功率超声纵弯谐振变幅器设计理论与实验研究
2018-04-24付俊帆秦慧斌
付俊帆, 秦慧斌, 吕 明
(1.中北大学 先进制造技术山西省重点实验室,太原 030051; 2.太原理工大学 精密加工山西省重点实验室,太原 030024)
功率超声纵弯谐振变幅器是一种新型复合振动模式的变幅器。该变幅器由变幅杆和环盘负载组成,变幅杆的纵向振动激励环盘负载作节圆型横向弯曲振动,实现两种不同振型的复合。在旋转超声加工领域,纵弯谐振变幅器将轴向超声振动引入刀具的旋转加工运动,可降低宏观切削力与切削热,具有精度高、效率高、成本低等优势[1];在超声清洗、超声换能器等声学应用领域,纵弯谐振变幅器的环盘负载由于辐射面积大、功率大、带宽大等特点,相比于纵振换能器具有较高的声辐射效率[2];此外,纵弯谐振变幅器在金属疲劳检测领域中亦有研究与应用[3]。纵弯谐振变幅器作为超声谐振系统的关键,其设计理论对超声加工、超声处理等应用具有重要影响。
自从变幅杆与阶梯圆盘组成的纵弯谐振变幅器由Barone等[4]提出之后,其振动特性与设计方法便一直得到研究人员的关注。Gallego-Jurez等[5-6]基于有限元法设计了圆盘、阶梯盘、矩形板等不同形状负载的纵弯谐振变幅器,并利用其振动特性和声学特性设计了多种声学装置。He等[7]利用有限元法研究了变幅杆激励面积对矩形板谐振频率、振动节线、振型等振动特性的影响。类似地,Ning等[8]利用有限元法分析了变幅杆振动频率对阶梯圆盘振动特性的影响。同样基于有限元法,Yamamoto等[9]设计了一种具有纵弯谐振模式的Tonpilz水声换能器,扩大了换能器带宽。在此基础上,Kim等[10-11]将回归分析与有限元法相结合,对纵弯谐振模式的Tonpilz水声换能器进行了优化设计,进一步扩大了带宽范围。
虽然有限元法是一种有效的变幅器设计方法,但多用于验证变幅器的振动特性,其设计周期较长,效率较低,需要提出一种理论设计方法来代替。Lin[12]基于等效电路法对薄圆盘负载的纵弯谐振变幅器进行了振动特性的分析,其谐振试验结果与的理论结果相吻合。王时英等[13]将齿轮简化为薄圆盘,采用力耦合的方法建立了变幅器振动模型,提出了超声珩齿变幅器设计方法。而吕明等[14]在此基础上将齿轮简化为中厚板环盘,既扩大了振动模型对齿轮的适用范围,也提高了设计精度。上述研究中的变幅器均采用单一材料,试验中所使用的环盘负载均为等厚度环盘。而在实际情况中,变幅器可能是由多种材料组成,环盘负载也多为阶梯环盘结构。如常见的变幅杆材料有铝、钛、钢等多种合金;珩磨轮是由铸铁轮毂、胶木腹板、树脂及磨料的轮缘组成的阶梯环盘;在实际加工中,车间工人不仅会将砂轮加工成阶梯环盘形状以便适应加工零件形状,也会在砂轮上安装钢制法兰以便安装。
本文将多材料因素考虑进变幅器的振动模型中,选择阶梯环盘作为负载,并将其视为三个等厚度环盘的组合体,基于Mindlin理论分析环盘单元横向弯曲振动的横向位移、转角、弯矩和剪力。根据环盘单元和变幅杆的连续条件和边界条件,建立纵弯谐振变幅器的振动模型与频率方程,并开发相应的设计软件。通过有限元模态分析和阻抗分析试验对该设计方法的准确性进行验证,为纵弯谐振变幅器的设计提供一种思路与手段。
1 纵弯谐振变幅器数学模型
纵弯谐振变幅器由变幅杆和环盘负载组成,本文以圆锥变幅杆和三阶梯环盘为例,其结构如图1所示。三阶梯环盘由不同材料的环盘1、2、3组成,三个环盘的中性面为同一平面。阶梯环盘中心孔与变幅杆芯轴过渡配合,并通过紧固螺母刚性连接。忽略键槽、圆角和倒角等微小结构对振动的影响。紧固螺母与变幅杆芯轴的尺寸相对变幅器较小,故在理论分析中忽略。
以变幅杆大端中心点为原点,以变幅杆中心轴线为z轴,建立如图1所示的(r,θ,z)圆柱坐标系。R1、R2分别表示圆锥变幅杆大端、小端半径,L表示变幅杆长度。R3、R4、R5分别表示环盘1、2、3的内径,R6表示环盘3的外径。t1、t2、t3分别表示环盘1、2、3的厚度。由于变幅杆和各个环盘的材料不尽相同,故分别以ρ1、ρ2、ρ3和ρ4表示环盘1、2、3和变幅杆的密度,E1、E2、E3和E4表示环盘1、2、3和变幅杆的弹性模量,μ1、μ2、μ3表示环盘1、2、3的泊松比。
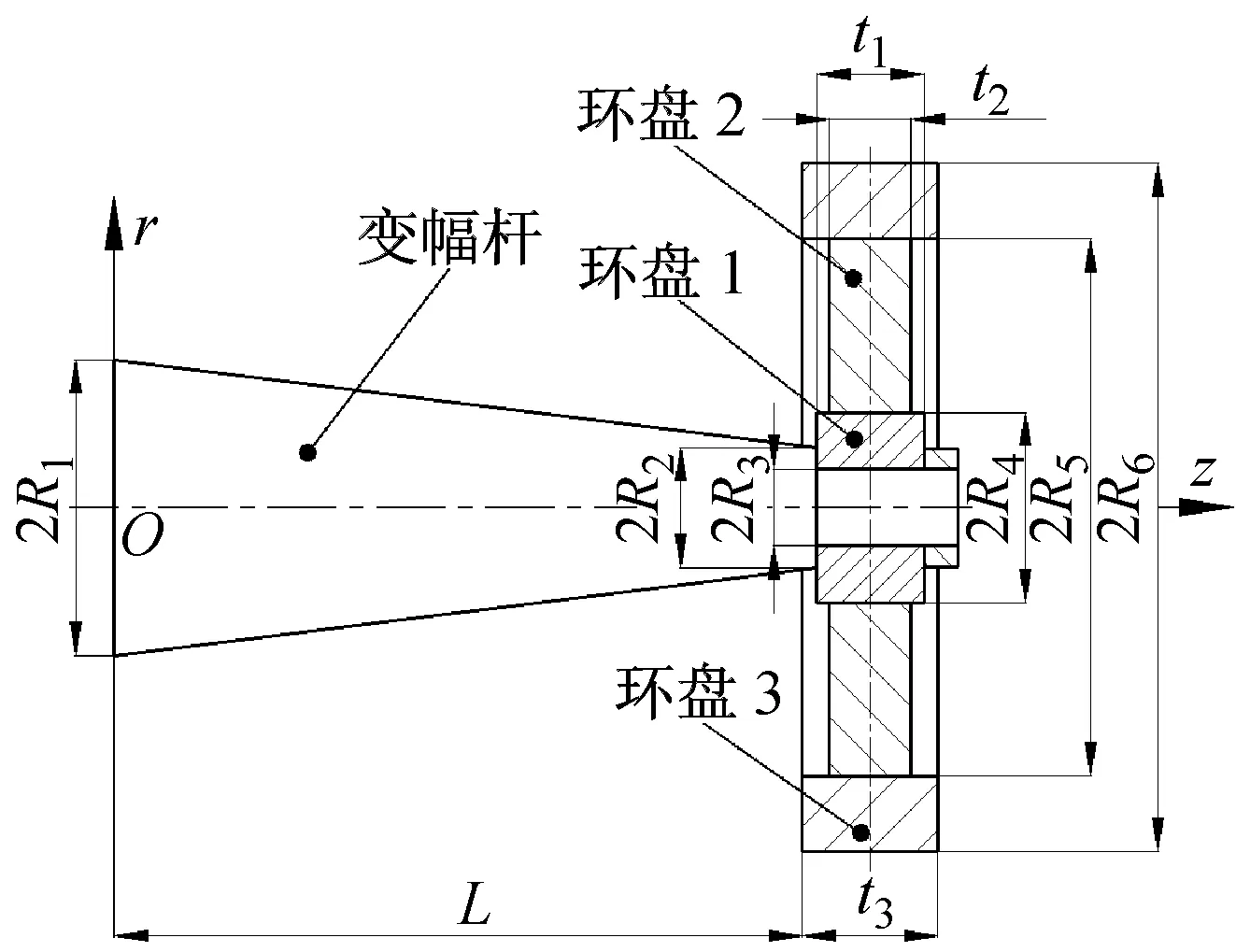
图1 纵弯谐振变幅器结构示意图
当变幅器作纵弯谐振时,变幅杆作纵向振动,其纵向位移ξ的解析表达式为
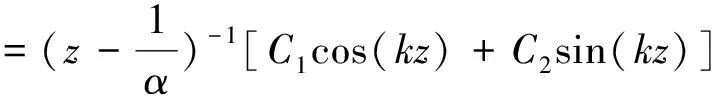
(1)
其中,圆波数k=ω/c,圆频率ω=2πf,变幅杆的纵波波速c=(E4/ρ4)1/2,C1、C2为由边界条件确定的待定常数。
Mindlin理论主要解决中厚板动力学问题,但也兼容薄板理论。基于Mindlin理论分析环盘振动,既扩大了环盘模型的适用范围,也可以提高计算精度。当变幅器作纵弯谐振时,环盘单元在纵振变幅杆的激励下作横向弯曲振动。由文献[15]可知,单个环盘的径向弯矩分量Mri和径向剪力分量Qri的表达式为
(2)
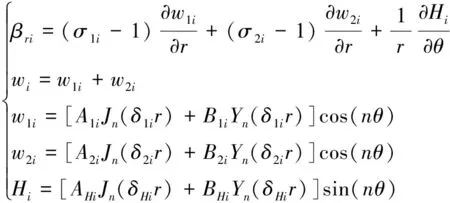
(3)
式(3)中
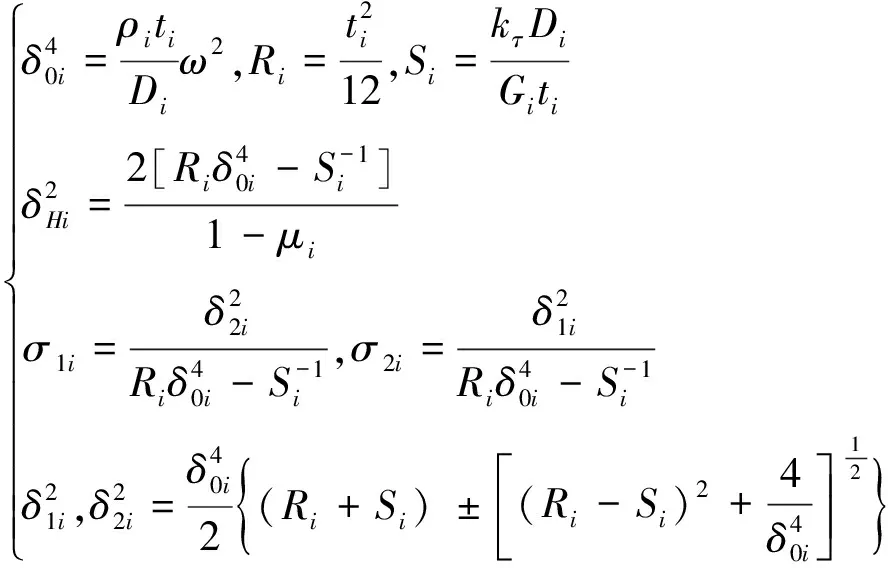
(4)
其中,Aji、Bji(j=1,2;i=1,2,3)为环盘i的由边界条件确定的待定常数,Jn(·)、Yn(·)分别为第一类、第二类贝塞尔函数。在超声处理或超声加工中,为了获得较好的声辐射特性或加工效果,通常使环盘负载作节圆型横向弯曲振动,即节径数为零[16]。因此n=0,式(3)可简化为
(5)
将式(5)代入式(2),可得径向弯矩分量Mri和径向剪力分量Qri的解析表达式为
(6)
当变幅器作纵弯谐振时,变幅杆大端在换能器的作用下纵向振动,应力为零,故有自由边界条件
(7)
变幅杆小端与环盘负载通过紧固螺母连接,近似刚性连接,故在z=L、r=R2处变幅杆与环盘1接触的环形面上存在有沿z轴方向的力与位移的连续条件;由于环盘无径向转动,故在r=R3处,环盘1的径向转角βr1为零,即
(8)
环盘2分别与环盘1在r=R4处,和环盘3和r=R5处满足横向位移wi、径向转角βri、径向弯矩分量Mri和径向剪力分量Qri的连续条件
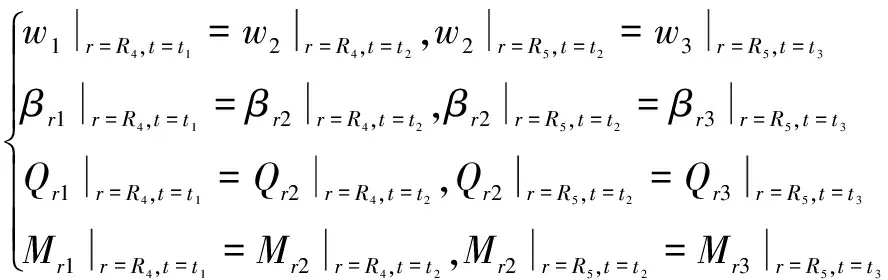
(9)
环盘3外缘为自由边界条件,故有
(10)
将式(1)和式(5)、(6)代入式(7)~(10)并整理,可得如下的齐次方程组
Δ14×14ζ14×1=014×1
(11)
其中
(12)
ζ14×1=[C1C2A11A21B11B21A12A22B12B22A13A23B13B23]T
(13)
Dpq(p,q=1,2,3,…,14)均为待定常数Aji、Bji、Cj(j=1,2;i=1,2,3)的系数,由变幅器的尺寸参数、材料系数和设计频率决定。当待定常数不全为0时,其充要条件为
Δ14×14=0
(14)
式(14)即为纵弯谐振变幅器的频率方程。当已知变幅器的尺寸和组成材料及其材料性能参数时,可根据频率方程求出变幅器的纵弯谐振频率。反之,当确定了设计纵弯谐振频率,并根据工程需要确定了变幅器的组成材料和除设计尺寸之外的其他尺寸时,可由频率方程求出设计尺寸。
通过改变各个环盘的材料参数与尺寸参数,可以实现不同类型的环盘负载的变化。如,当三个环盘的材料参数相同时,环盘负载成为单一材料的环盘;当相邻的两个或三个环盘的厚度相同时,环盘负载成为等厚度环盘。
2 纵弯谐振变幅器设计软件
基于MATLAB/GUI开发了如图2所示的纵弯谐振系统设计软件,设计尺寸为变幅杆长度L。该软件采用数值法求解频率方程,以固定步长计算并绘出L-Δ的曲线图(如图3),曲线与横坐标轴的交点即为求解结果。软件的流程图如图4所示。
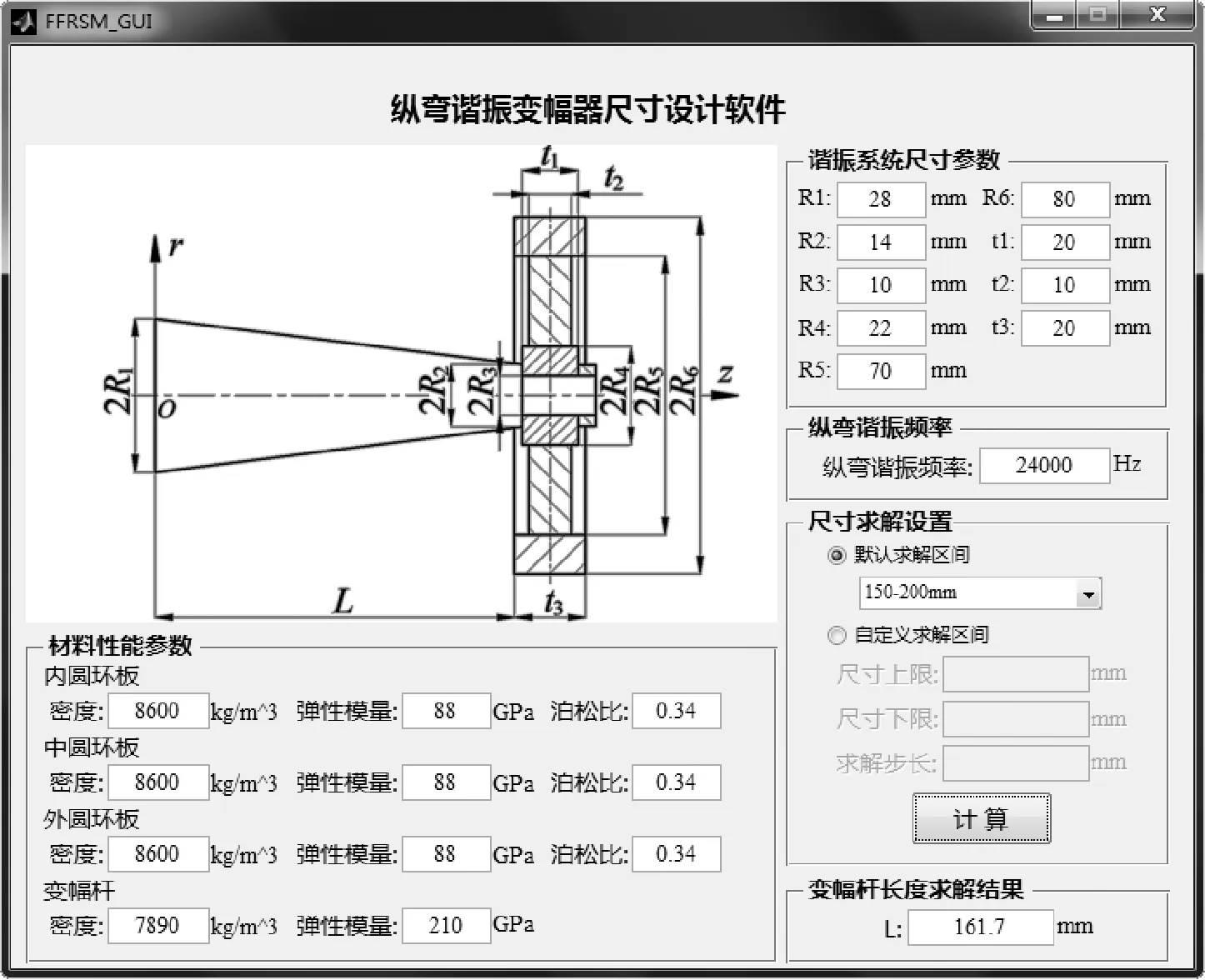
图2 纵弯谐振变幅器设计软件
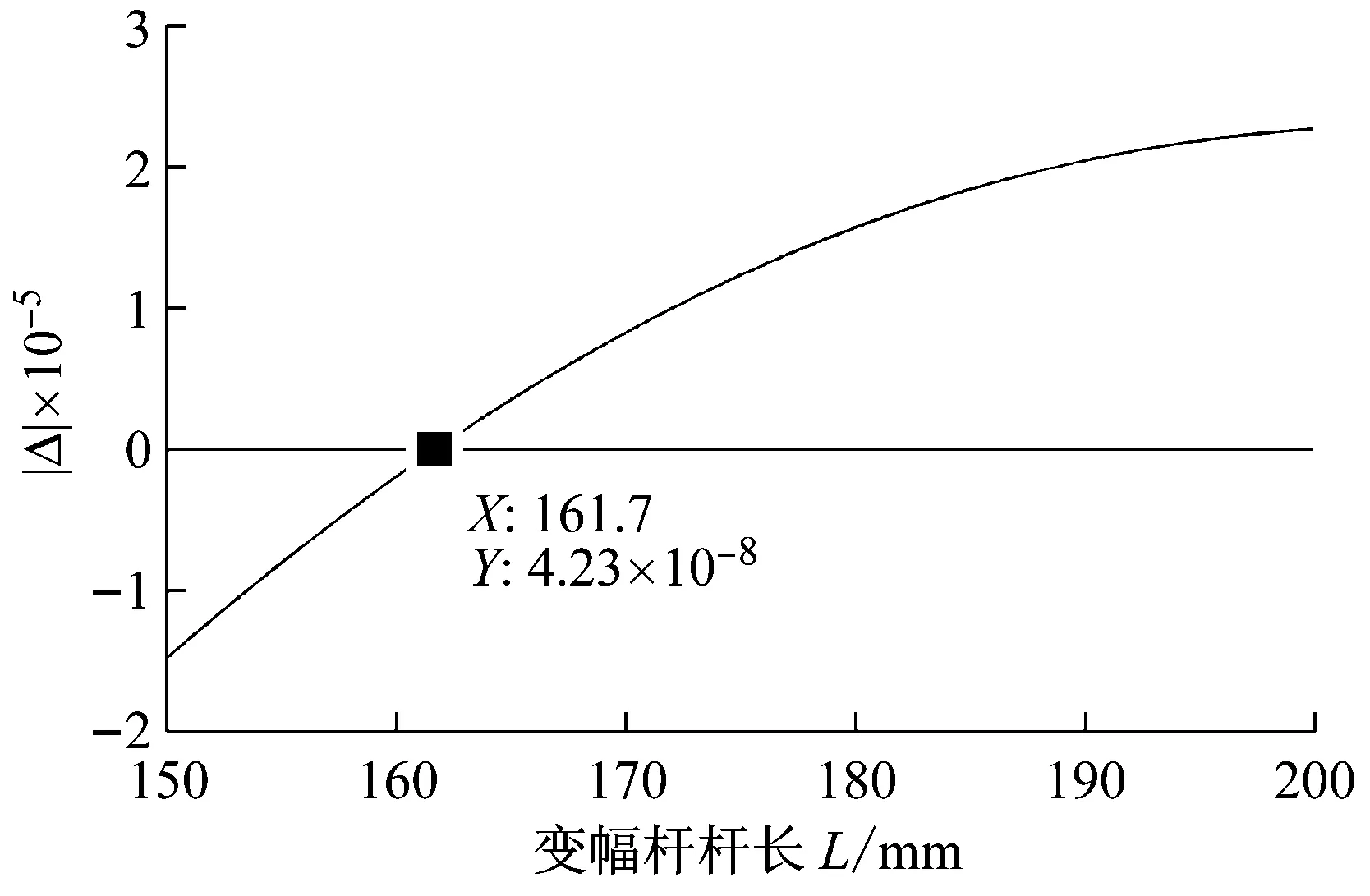
图3 L-Δ求解曲线
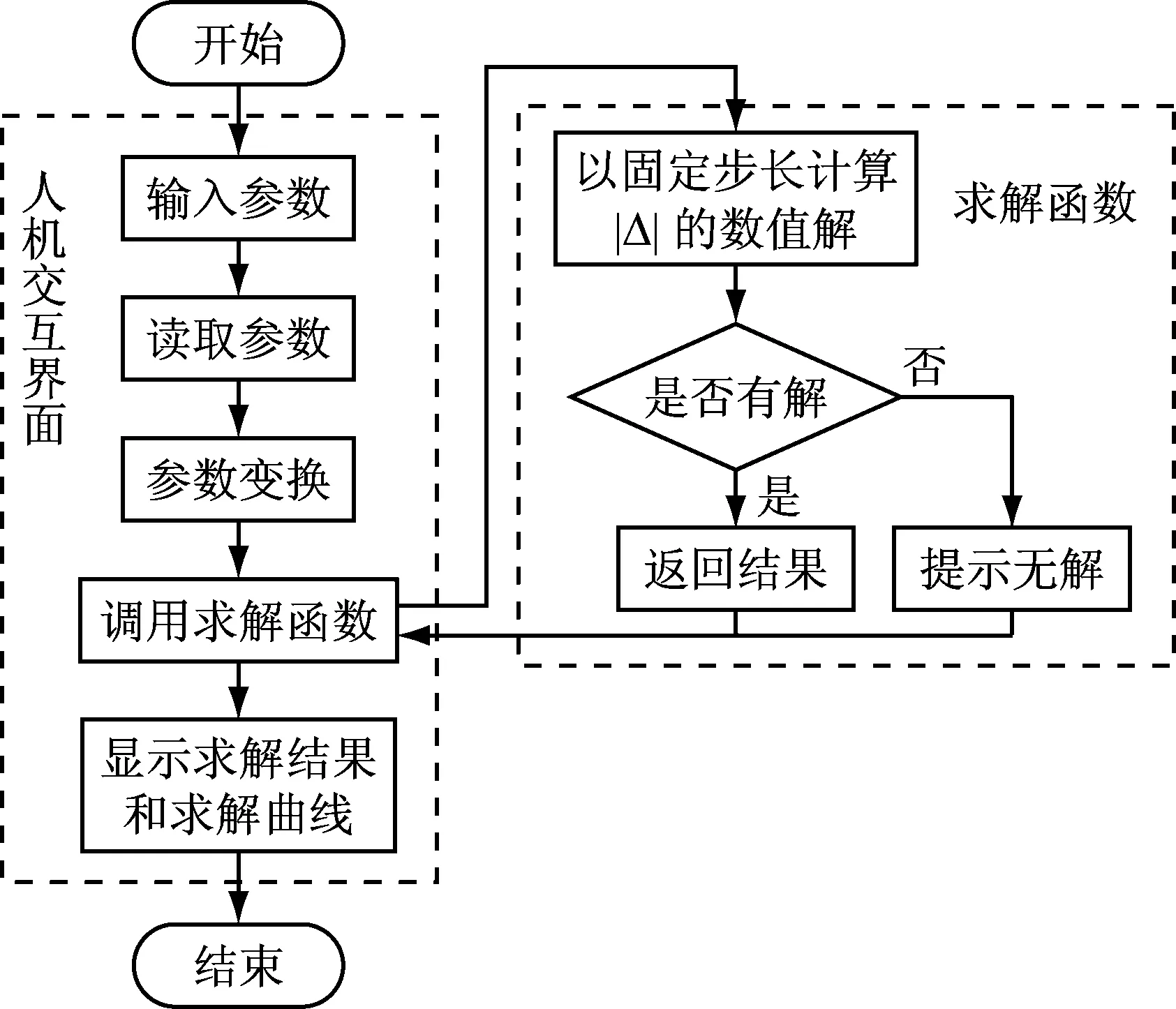
图4 设计软件流程图
由软件流程图可知,该软件主要由人机交互界面和求解函数两部分构成。人机交互界面为设计人员提供一个简洁直观的操作与显示界面,用户只需对按钮、输入框、下拉菜单等对象进行操作即可完成各种程序命令。软件的计算功能由求解函数完成,用户输入的数据由人机交互界面传递给求解函数,求解函数将计算结果返回给人机交互界面,并由人机交互界面显示求解结果与求解曲线。该软件降低了变幅器设计对设计人员的理论水平的要求,可缩短设计时间,提高设计效率。
3 试 验
3.1 有限元模态分析与阻抗分析试验
为验证上述的纵弯谐振变幅器设计理论,利用纵弯谐振变幅器设计软件设计了三个纵弯谐振变幅器。变幅器1由45钢变幅杆与黄铜H62阶梯环盘组成,设计频率为24 kHz;变幅器2由45钢变幅杆和灰铸铁HT200的阶梯环盘组成,设计频率为22 kHz;变幅器3由45钢变幅杆和磨料浓度为100%的铝基酚醛树脂结合剂金刚石砂轮组成,设计频率为21 kHz。各个变幅器的材料结构如表1所示,其中“—”表示不存在该结构。各个材料的性能参数如表2所示。变幅杆长度L为设计尺寸,由设计软件计算求出,其他变幅器尺寸均为已知尺寸。变幅器已知尺寸、设计频率和设计尺寸理论结果如表3所示。
根据上述参数在SolidWorks中建立相应的纵弯谐振变幅器模型,导入至有限元分析软件ANSYS中。粘结实体后,设置材料属性并用Solid 95单元对不同实体进行5级精度的智能网格划分。有限元模态分析采用Block Lanczos法,提取20~25 kHz的变幅器谐振模态。变幅器的纵弯谐振振型如图5所示,纵弯谐振频率如表4中fA行所示。

表1 纵弯谐振变幅器的材料结构
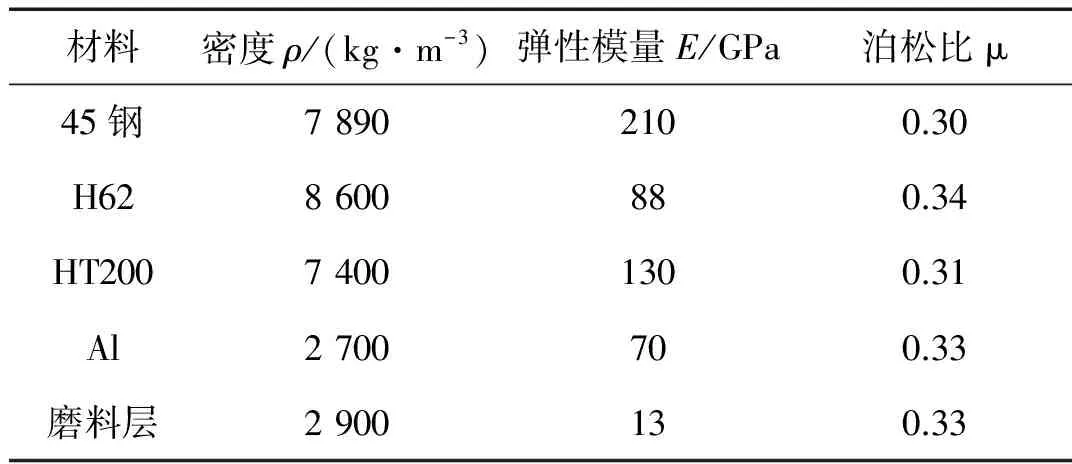
表2 材料性能参数

表3 纵弯谐振变幅器尺寸参数与设计频率

(a)变幅器1在23422Hz的振型(b)变幅器2在21765Hz的振型
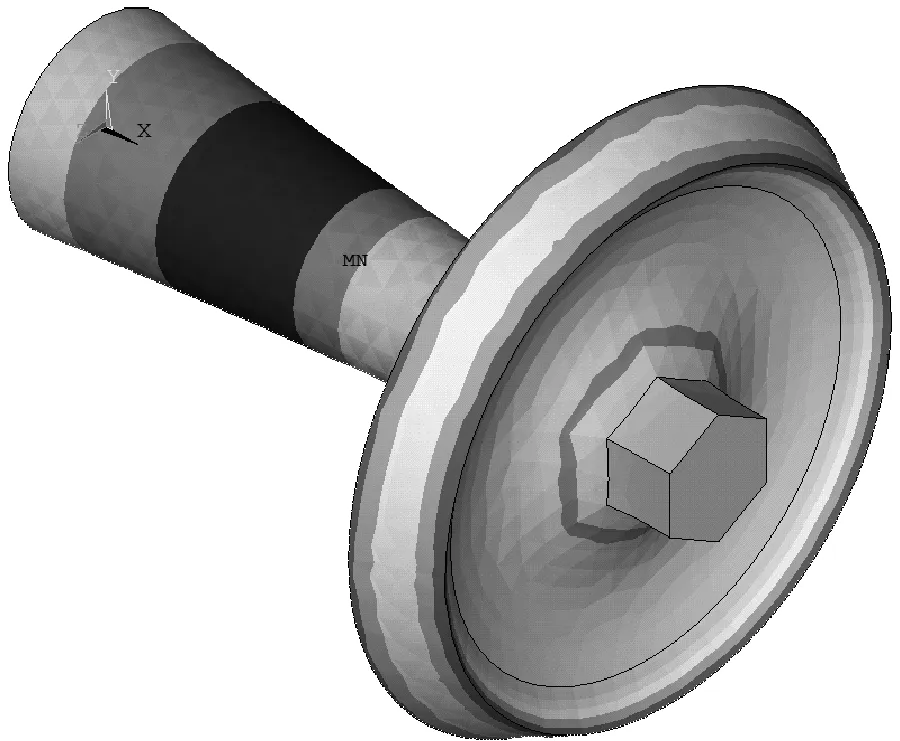
(c) 变幅器3在20 076 Hz的振型
根据表3加工了45钢变幅杆、黄铜H62阶梯环盘和灰铸铁HT200阶梯环盘,购置了酚醛树脂金刚石砂轮。通过紧固螺母分别装配为变幅器1、2、3(如图6)。通过螺纹将变幅器与超声换能器连接在一起,并在连接面上涂抹凡士林填充两者之间的微小间隙,减小超声波在连接面的反射损失。用导线将阻抗分析仪PV70A与超声换能器相连接(如图7),利用相应软件测量变幅器的纵弯谐振频率,测量结果如表4中fE行所示,导纳圆曲线和幅相特性曲线分别如图8、图9所示。
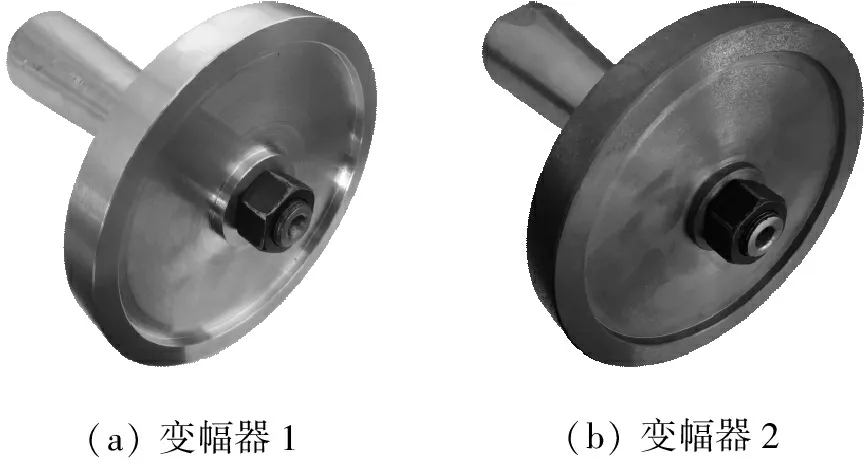
(a)变幅器1(b)变幅器2

(c) 变幅器3

图7 变幅器阻抗分析试验
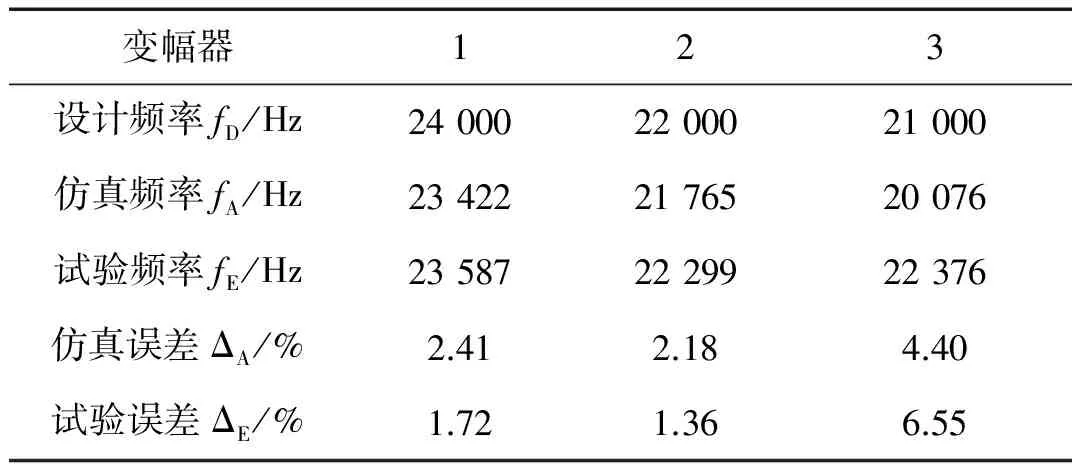
变幅器123设计频率fD/Hz240002200021000仿真频率fA/Hz234222176520076试验频率fE/Hz235872229922376仿真误差ΔA/%2.412.184.40试验误差ΔE/%1.721.366.55
表4中,fD为纵弯谐振变幅器的设计频率;ΔA=fA-fD/fD,为有限元模态分析频率与设计频率的误差;ΔE=fE-fD/fD,为阻抗分析试验测得的频率与设计频率的误差。
由表4可知,仿真频率的最大误差为4.40%,试验频率的最大误差为6.55%。因此有限元仿真和阻抗分析试验得到的纵弯谐振频率结果与设计频率基本一致,证明了上述的纵弯谐振变幅器设计方法对工程设计具有一定的参考意义。
图8中三个变幅器的导纳曲线都呈现较完整的单圆,说明所测谐振频率准确,换能器与变幅器的阻抗匹配较好。但依然有局部的导纳曲线和幅相特性曲线出现畸变,可能是因为变幅器装配质量不佳导致变幅器的机械损耗较大,致使动态电阻较大。这一点从变幅器1和2的导纳圆的半径均较小中也能得到验证。因此,在装配时需要在接触面上涂抹凡士林,并多次调试安装变幅器,减小机械损耗,提高阻抗匹配性能。
造成变幅器的仿真误差和试验误差的因素,可能有以下三点:
(1) 在振动模型中忽略了螺母,而在实际情况中螺母对变幅器的刚度与质量具有影响,从而影响谐振频率。
(2) 螺母的预紧力对谐振频率也有一定影响[17]。振动模型中,变幅杆与环盘负载通过紧固螺母实现近似刚性连接,其前提条件为螺母预紧力足够大。而在试验中,螺母预紧力可能不足,影响变幅器刚度。
(3) 由于超声振动在不同材料的边界上会发生不同程度的反射,从而造成损耗、噪声、阻抗失配等问题,最终影响了变幅器的纵弯谐振频率的设计误差。
因此在变幅器理论设计后,可利用有限元法将上述影响考虑进来,进一步修正纵弯谐振变幅器的设计尺寸。
3.2 超声谐振试验
利用变幅器3和频率为20 kHz的ZJS-2000型超声波发生器进行了超声谐振试验,试验装置如图10所示。变幅器和换能器通过螺纹分别与传振杆的上下端相连。传振杆的法兰位于振动节点处,通过细牙螺栓固定在试验台上。换能器通过电缆与超声发生器相连。
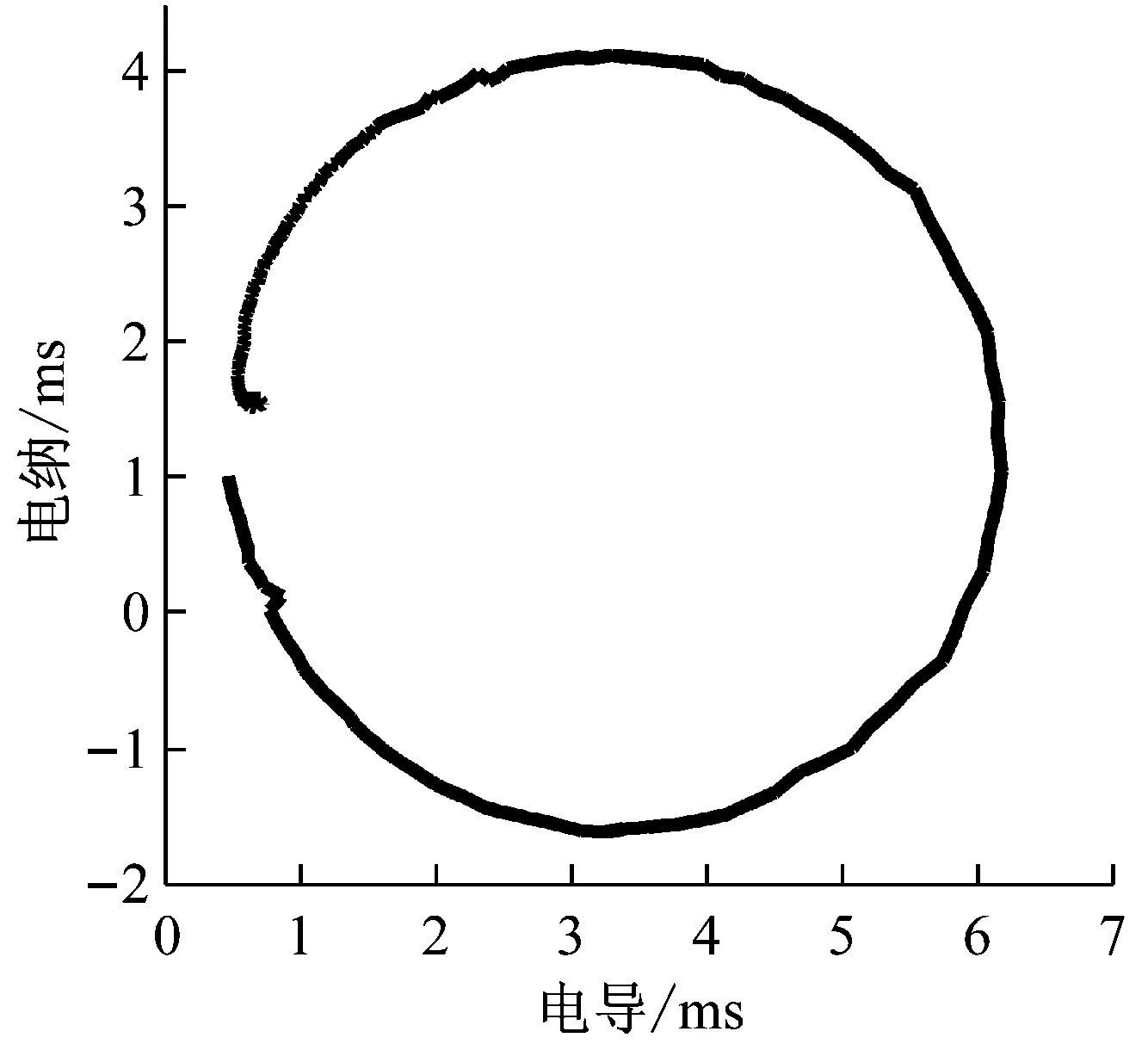
(a) 变幅器1的导纳曲线
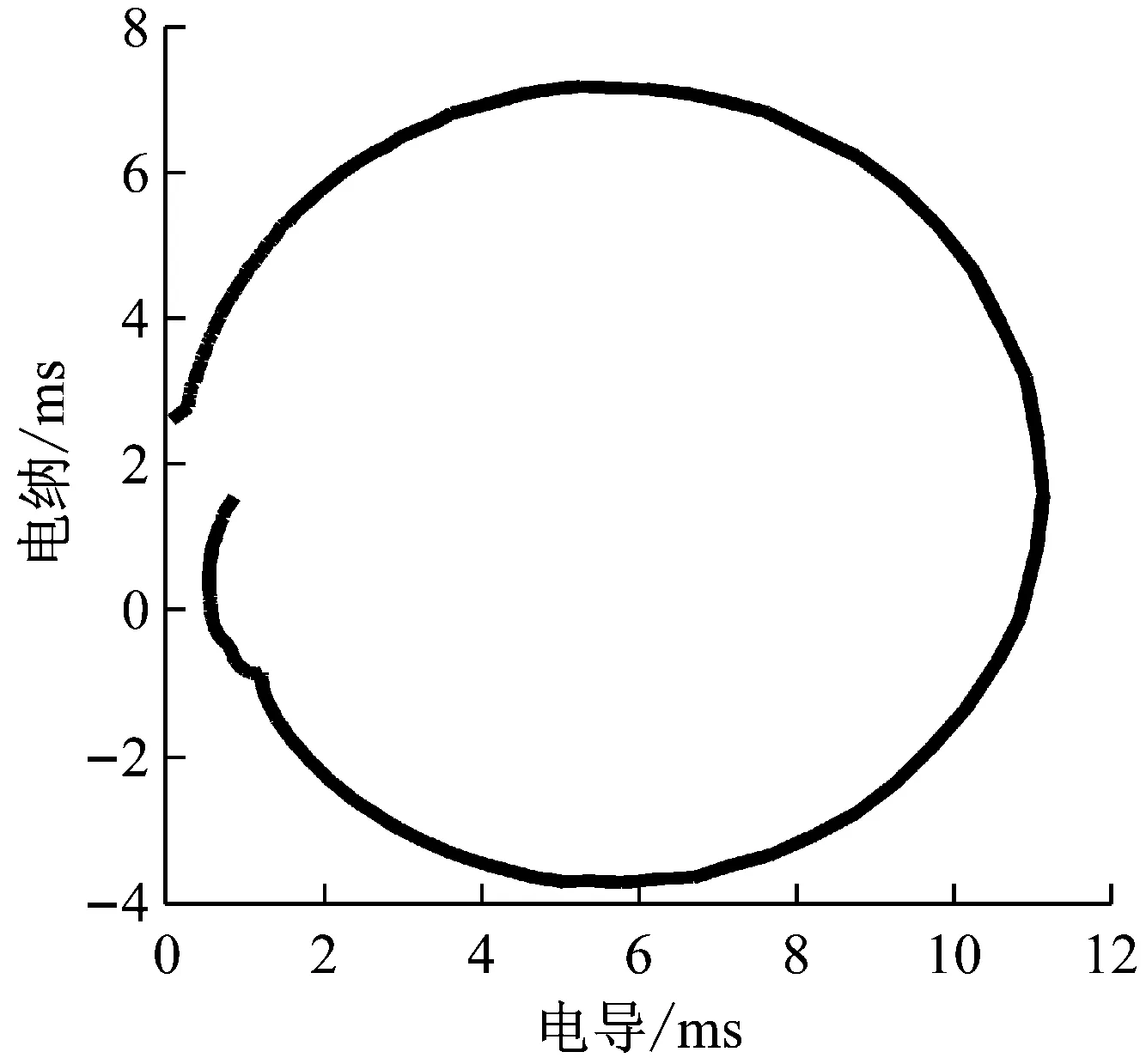
(b) 变幅器2的导纳曲线
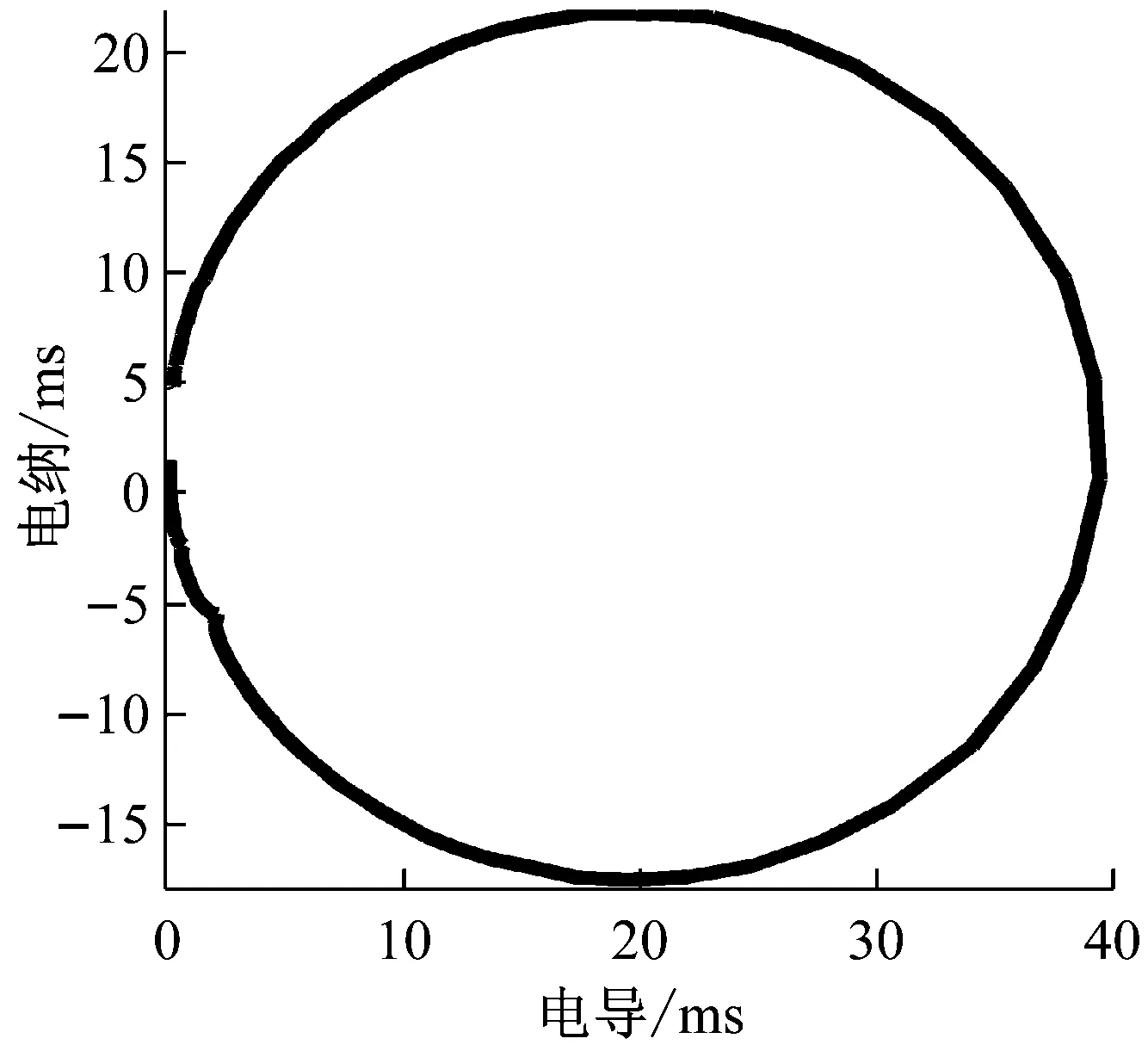
(c) 变幅器3的导纳曲线
在砂轮表面均匀撒上碳化硅颗粒,启动超声发生器,调节调频螺丝。当超声发生器上显示的振动频率为fR=21 212 Hz时,碳化硅颗粒聚集为一个直径为122.3 mm的圆环,如图11所示。该现象证明了砂轮正在作节圆型横向弯曲振动,振动节线为圆形,与图5(c)中环盘负载的振型一致。该谐振频率fR与变幅器3的纵弯谐振设计频率fD=21 000 Hz相差212 Hz,试验误差为ΔD=fR-fD/fD=1.01%。该试验证明了通过纵弯谐振变幅器设计方法设计的变幅器能够达到较为理想的纵弯谐振效果。
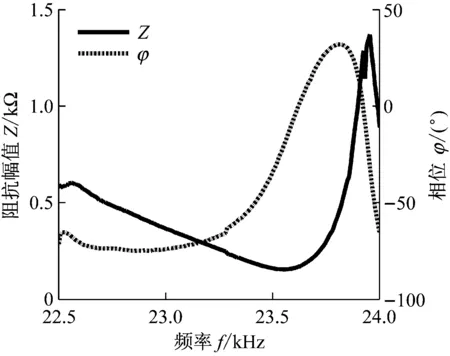
(a) 变幅器1的幅相特性曲线
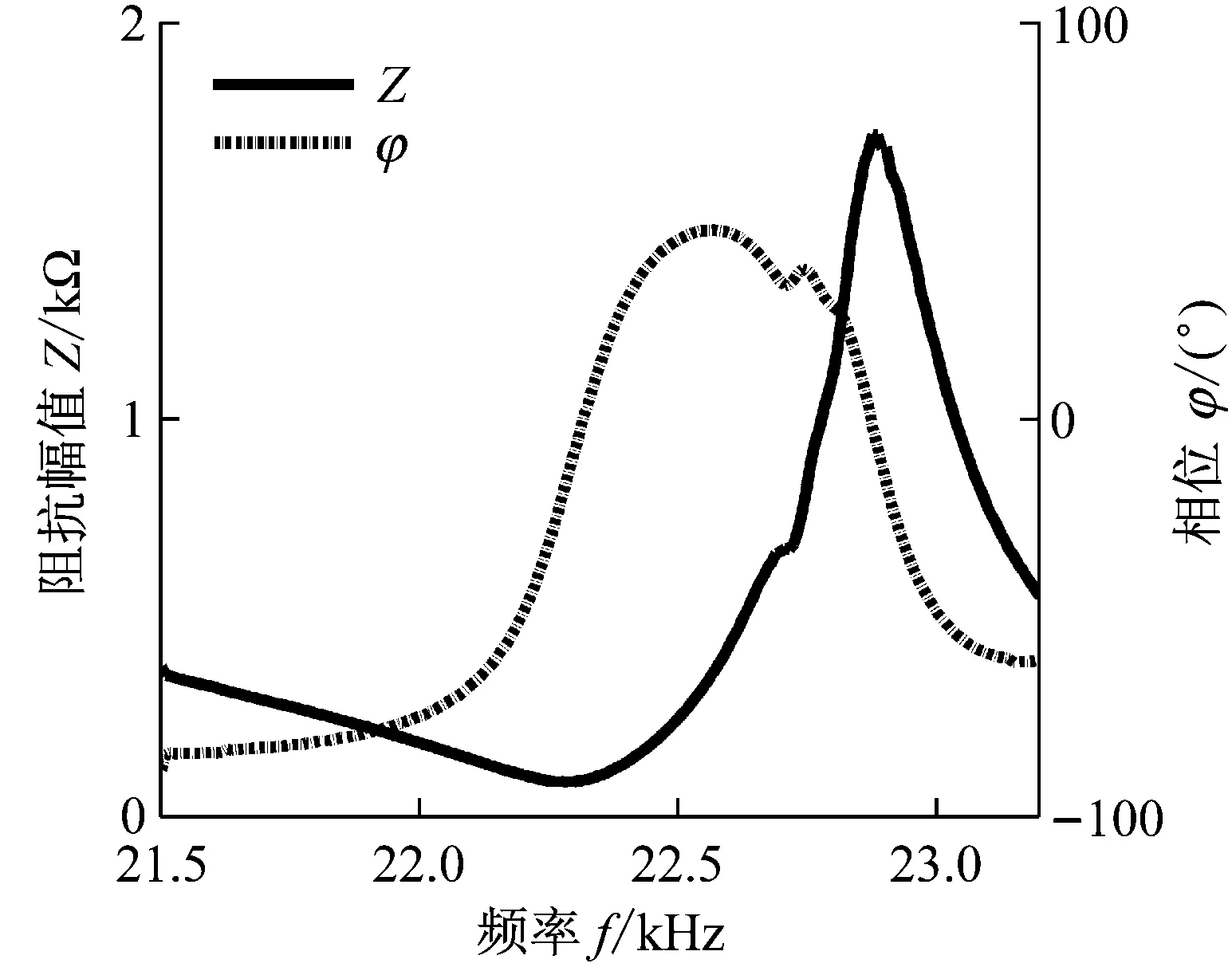
(b) 变幅器2的幅相特性曲线
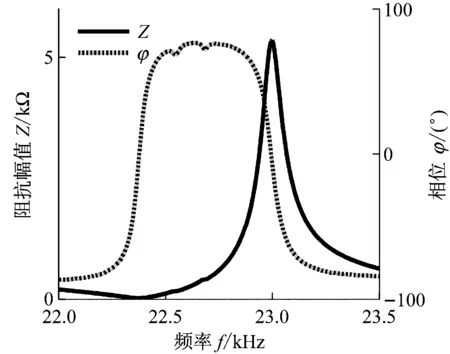
(c) 变幅器3的幅相特性曲线

图10 超声谐振试验装置

图11 谐振频率为21 212 Hz时的圆形振动节线
4 结 论
本文提出了一种多材料的纵弯谐振变幅器的设计方法,基于Mindlin理论分析了环盘单元的横向弯曲振动,通过振动单元之间的连续条件和边界条件建立了纵弯谐振变幅器振动模型并推导了振动方程,利用MATLAB/GUI开发了变幅器设计软件。有限元模态分析、阻抗分析试验和超声谐振试验的结果表明:
(1) 基于Mindlin理论的纵弯谐振变幅器设计方法具有较好的设计精度,能兼容薄环盘和中厚环盘负载,可为多材料的纵弯谐振变幅器的设计提供参考。
(2) 纵弯谐振变幅器设计软件可为设计人员提供一种简洁直观的设计手段,可降低理论设计的门槛,提高设计效率。
(3) 螺母、预紧力和不同材料界面上的超声反射对谐振频率存在影响,可在理论设计的基础上用有限元法进一步修正设计参数。
[1] WANG Y,LIN B,WANG S,et al.Study on the system matching of ultrasonic vibration assisted grinding for hard and brittle materials processing[J].International Journal of Machine Tools and Manufacture,2014,77:66-73.
[3] CAMPOS-POZUELO C,VANHILLE C,GALLEGO-JUREZ J A.Comparative study of the nonlinear behavior of fatigued and intact samples of metallic alloys[J].IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control,2006,53(1): 175-184.
[4] BARONE A,GALLEGO-JUREZ J A.Flexural vibrating free-edge plates with stepped thicknesses for generating high directional ultrasonic radiation[J].The Journal of the Acoustical Society of America,1972,51(3B):953-959.
[7] HE X,YAO J,ZHANG H,et al.Effects of excitation area of longitudinal transducer on the flexural vibration characteristics of a rectangular plate in stripe mode[J].Ultrasonics,2015,58:104-110.
[8] NING J,HE X,ZHAO G.Effects of driving frequency of longitudinal transducer on the vibration characteristics of a stepped plate[J].Applied Acoustics,2014,79:164-168.
[9] YAMAMOTO M,SHIBA H,FUJII T,et al.Tonpilz piezoelectric transducer with a bending piezoelectric disk on the radiation surface[J].Japanese Journal of Applied Physics,2003,42(5S):3221-3224.
[10] KIM H,ROH Y.Design and fabrication of a wideband Tonpilz transducer with a void head mass[J].Sensors and Actuators A: Physical,2016,239:137-143.
[11] YONGRAE R,HYUNKI K.Design and fabrication of a wideband tonpilz transducer with a cavity-type head mass[C]//Processing of Symposium on Ultrasonic Electronics.Tsukuba:Steering Committee of Symposium on Ultrasonic Electronics,2015.
[12] LIN S.Radiation impedance and equivalent circuit for piezoelectric ultrasonic composite transducers of vibrational mode-conversion[J].IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control,2012,59(1):139-149.
[13] 王时英,吕明,轧刚.基于力耦合的非谐振单元组成的超声变幅器设计[J].振动与冲击,2012,31(11):104-107.
WANG Shiying, LÜ Ming, YA Gang. Design of an ultrasonic transducer with non-resonant units based on force coupling [J]. Journal of Vibration and Shock, 2012, 31(11): 104-107.
[14] 吕明,王时英,秦慧斌.非谐振设计理论与齿轮超声加工[M].北京:科学出版社,2014.
[15] HOSSEINI-HASHEMI S,BEDROUD M,NAZEMNEZHAD R.An exact analytical solution for free vibration of functionally graded circular/annular Mindlin nanoplates via nonlocal elasticity[J].Composite Structures,2013,103:108-118.
[16] WANG S,LÜ M,YA G,et al.Theoretical and experimental research on design of non-resonant gear transformer[C]//Proceedings of the ASME 2014 International Mechanical Engineering Congress and Exposition. Montreal:American Society of Mechanical Engineers,2014.
[17] 佘银柱.超声珩齿非谐振单元变幅器的设计理论与实验研究[D].太原:太原理工大学,2012.
