远场长周期地震动频谱特征周期与强度指标研究

王 博， 刘伯权， 吴 涛， 代慧娟

(1. 长安大学 建筑工程学院，西安 710061； 2. 西安科技大学 建筑与土木工程学院，西安 710054)

远场长周期地震动因含有丰富的长周期成分而易使超高层建筑、大跨桥梁、大型储液罐等长周期结构发生震害[1]。现行抗震设计理论由于未充分考虑远场长周期地震动的影响而不能确保长周期结构的抗震安全。长周期地震动对长周期结构的影响研究已成为十分重要和紧迫的课题[2]，其中，进行远场长周期地震动参数研究是长周期地震危险性分析的基础，也是长周期地震动抗震设防的首要工作[3]。我国现行抗震设计规范尚未有针对远场长周期地震动频谱特征周期的相关规定，这不可避免地会给受远场长周期地震动威胁地区的地面运动预测、地震危险性评价以及震害预测等工作带来较大误差。因此，有必要对远场长周期地震动的频谱特征周期进行系统分析。此外，我国现行《建筑抗震设计规范》[4]采用峰值加速度PGA作为抗震分析用强度指标，在进行结构时程反应分析时，将所选地震波按照抗震设防烈度对应的峰值加速度PGA进行调幅。既有研究表明，远场长周期地震动与普通地震动的产生机理及特性明显不同[5-7]，峰值加速度PGA能否作为远场长周期地震动的抗震分析用强度指标有待进一步研究。

鉴于此，本文选择12种代表性地震动频谱特征周期参数与20种代表性地震动强度指标，基于40条远场长周期地震动数据，采用MATLAB编制程序，计算分析其频谱周期特性及强度指标与最大地震响应间的相关性，最终，建议适用于远场长周期地震动的频谱特征周期表征参数与抗震分析用强度指标。

1 远场长周期地震动的选择

由于远场长周期地震动实际记录数据偏少，在确保地震动数据可靠的基础上，本文选择40条远场长周期地震动记录进行计算与分析，如表1所示。这些记录主要来自美国太平洋地震工程研究中心数据库网站(http://peer.berkeley.edu/)。所选地震动记录均来自于1999-09-21台湾7.6级集集地震，PGA范围为11.15～179.81 cm/s2，PGV范围为2.13～58.95 cm/s，涵盖了不同强度的地震动记录。

2 远场长周期地震动频谱特征周期分析

2.1 频谱特征周期参数概述

已有的地震动频谱特征周期参数主要包括局部周期参数与平滑周期参数两类。其中，局部周期参数主要反映地震动的某一个频谱周期成分，主要包括由弹性加速度反应谱与速度反应谱提取出的谱峰值对应的周期参数TPA、TPV以及由地震动Fourier谱、边际谱与Hilbert能量谱提取出的卓越周期参数Tf、Tmar、TE等5种。平滑周期参数可反映地震动在一定频率范围内的平均频谱特性，属于整体量，主要包括以下7种。

表1 分析用远场长周期地震动基本信息

(1)特征周期Tg

ATC[8]定义的特征周期如式(1a)～式(1c)所示。

(1a)

EPA=Sa/2.5

(1b)

EPV=Sv/2.5

(1c)

式中：Sa与Sv分别为阻尼比取5%时拟加速度反应谱与拟速度反应谱在周期0.1～0.5 s间的平均值。

该周期参数由Yang等[9]基于有效峰值加速度IEPA与有效峰值速度IEPV改进而来，如式(2a)～式(2c)所示。

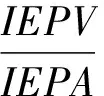
(2a)

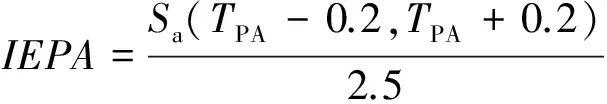
(2b)

(2c)

式中：TPA、TPV分别为加速度反应谱与速度反应谱谱峰值对应的周期。

(3)加速度反应谱特征周期Tc[10]

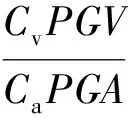
(3)

式中：Ca=2.5，Cv=2.0。

(4)平滑化反应谱卓越周期To[11]

该周期参数相当于将>1.2倍PGA强度下的加速度反应谱值进行平滑，如式(4)所示。

≥1.2，

ΔlgTi≤0.02

(4)

式中：Sa(Ti)为周期为Ti时对应的加速度反应谱值。

(5)平均谱周期Tavg

.05 s≤Ti≤4 s，

ΔTi≤0.05 s

(5)

(6)Fourier幅值谱平均周期Tm[12]

.25 Hz≤fi≤20 Hz，

Δf≤0.05 Hz

(6)

式中：Ci为Fourier幅值谱的纵坐标幅值。

(7)Hibert边际谱平均周期Tmh

.25 Hz≤fi≤20 Hz，

Δf≤0.05 Hz

(7)

式中：Hi为Hibert边际谱的纵坐标幅值。

2.2 远场长周期地震动频谱特征周期计算与分析

通过计算远场长周期地震动代表性频谱特征周期参数的平均值及各周期参数的变异系数进行分析。其中，变异系数计算方法同文献[13]，变异系数越小，说明其稳定性越好。表2为计算得到的各频谱特征周期参数的平均值与变异系数。

计算结果分析表明：

(1)不同周期参数的平均值与变异系数均不同。既有研究表明，特征周期Tg与To可反映地震动的短周期成分，而Tc、Tavg、Tm、Tmh可反映地震动的长周期成分。其中，Tm与Tmh是对地震动主要频段(0.25～20Hz)范围内频谱特性的表征，可有效反映地震动长周期成分的贡献。由表2可知，Tmh大于Tm，分析认为这是由于Tm在计算时采用的是地震动Fourier谱，易在地震动低频处低估低频成分，在高频处高估高频成分，而Tmh在计算时由于采用了比Fourier谱更有效反映地震动频谱特性的边际谱，因此可更为真实地反映远场长周期地震动的频谱周期特性。

表2 地震动频谱特征周期参数平均值与变异系数

(3)对于局部周期参数而言，由于其主要反映的是地震动某一个频谱周期成分，属于局部量，因此，不推荐采用该类参数来表征远场长周期地震动的频谱周期特性。同时可以看出，除TE外，其他局部周期参数的变异系数均较大，稳定性较差。

综上分析认为，对于远场长周期地震动而言，Hilbert边际谱平均周期Tmh属于平滑周期参数，既反映了地震动在主要频率范围内的平均频谱特性，又具有较高的稳定性，因此初步建议选用Hilbert边际谱平均周期Tmh作为远场长周期地震动的频谱特征周期表征参数。

3 远场长周期地震动强度指标分析

3.1 地震动强度指标概述

地震动强度指标主要包括加速度型强度指标、速度型强度指标与位移型强度指标三类。参考文献[14-16]选择20种代表性强度指标进行计算分析，包括9种加速度型强度指标(PGA、Ia、Pa、arms、Ic、Ea、ars、PSA、IA)、6种速度型强度指标(PGV、IV、IF、Ev、vrs、PSV)与5种位移型强度指标(PGD、Id、Ed、drs、PSD)。各强度指标概述如下：

(1)地震动峰值强度

主要包括峰值加速度PGA、峰值速度PGV与峰值位移PGD。

(2)Arias强度指标

该强度指标与结构单位质量总滞回耗能量相关，由Arias[17]提出，其表达式如式(8)所示

(8)

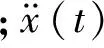
(3)Riddell强度指标

Riddell等[18]在总结既有强度指标的基础上提出如下三个地震动强度指标

(9)

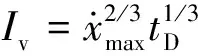
(10)

(11)

式中：tD为地震动强震持时，tD=t95-t5。

(4)Housner强度指标

Housner认为可通过输入结构单位质量的总能量在时间域内的平均值来衡量地震对结构的破坏能力，提出平均加速度平方指标[19]

(12)

文献[20]对式(12)开方得到如下强度指标

(13)

(5)Park-Ang强度指标

该强度指标也称为特征强度指标，由Park和Ang提出，能较好描述地震动强度与结构损伤指标间的关系[21]，其数学表达式为

(14)

(6)Nau和Hall强度指标

Nau等[22]对Arias强度指标进行简化，提出如下三个指标

(15)

(16)

(17)

对上述三个指标进行开方处理，又可以得到如下三个新的强度指标

(18)

(19)

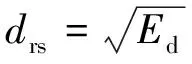
(20)

(7)Fajfar强度指标

Fajfar等[23]在研究了地震动强度与结构损伤程度及地震输入能量的关系后，提出以下强度指标

(21)

(8)谱峰值强度指标

主要包括加速度反应谱峰值PSA、速度反应谱峰值PSV与位移反应谱峰值PSD三种[24-25]。

3.2 强度指标的分析方法

合理的强度指标应与结构地震响应具有较好的相关性。本文通过对比分析远场长周期地震动代表性强度指标与双线性SDOF体系最大地震响应间的相关性，提出适用于远场长周期地震动的抗震分析用强度指标。具体步骤如下：

(1)弹塑性SDOF体系模型参数的确定。阻尼比取5%，采用双线性恢复力模型，屈服后刚度折减系数取0.05，延性系数取1.0(弹性)、2.0、3.0、5.0；自振周期从0.1 s到10 s，间隔0.1 s取值，共100种结构周期，总计400个SDOF体系分析模型。

(2)地震动强度指标及SDOF体系最大地震响应的计算。采用MATLAB编制程序，分别计算每条地震动的20个强度指标及各SDOF体系在每条地震动作用下的最大加速度响应、最大速度响应、最大位移响应、最大输入能及最大滞回耗能。

(3)地震动各强度指标与最大地震响应间的相关系数计算。根据第(2)步计算得到的地震动强度指标及SDOF最大响应，按照式(22)[26]计算得到每种强度指标与不同周期、不同延性系数下SDOF体系最大地震响应间的相关系数

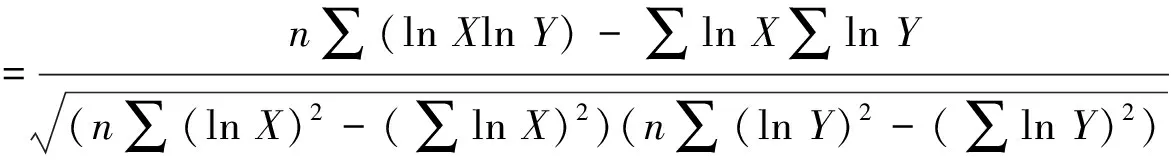
(22)

式中：X，Y分别是指地震动强度指标与最大地震响应。

(4)强度指标与最大地震响应的相关性对比分析

根据第(3)步计算得到的相关系数，对比分析不同强度指标与最大地震响应间的相关性，并分析结构周期与延性系数对相关性的影响规律。在此基础上，综合工程应用的便利性，选择相关性好的强度指标作为远场长周期地震动的抗震分析用强度指标。

3.3 远场长周期地震动强度指标分析

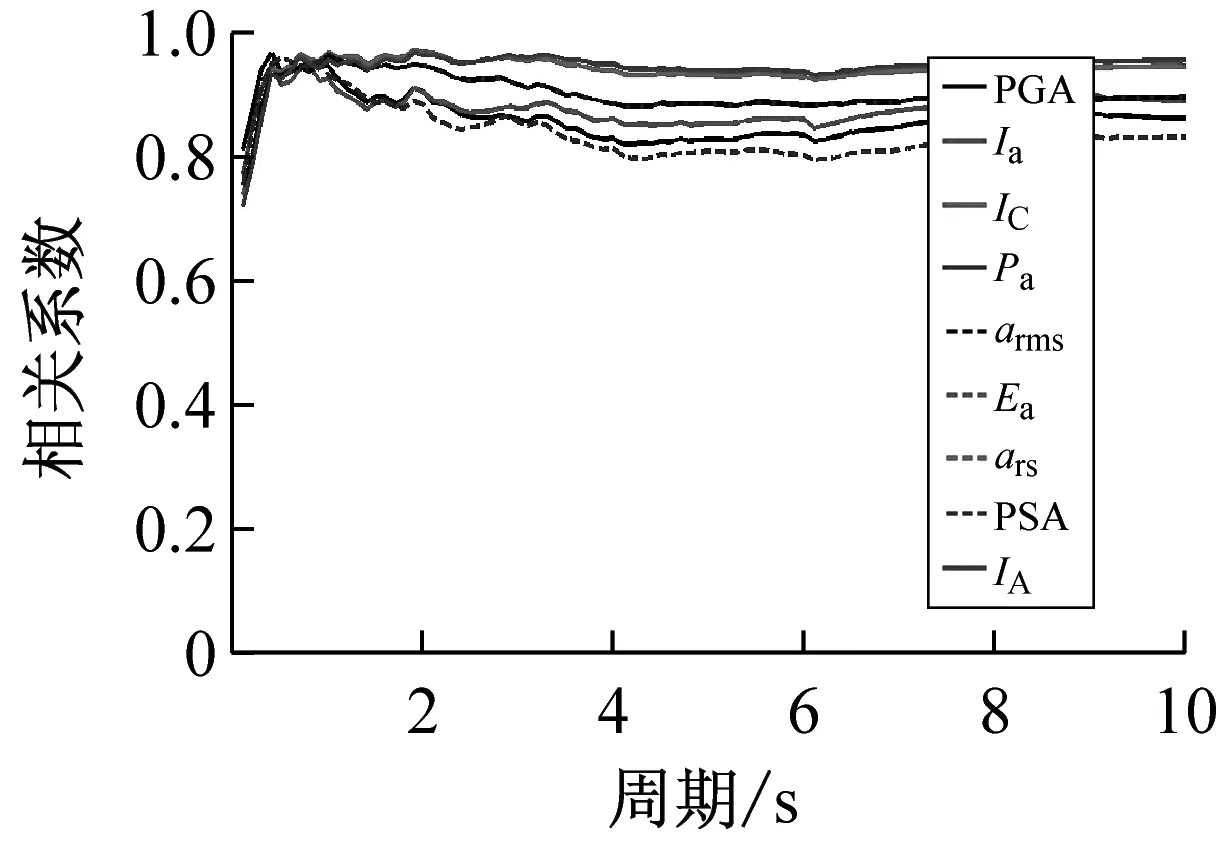
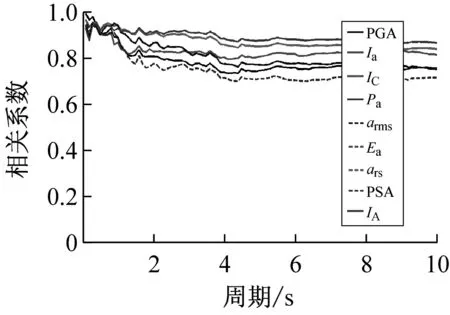
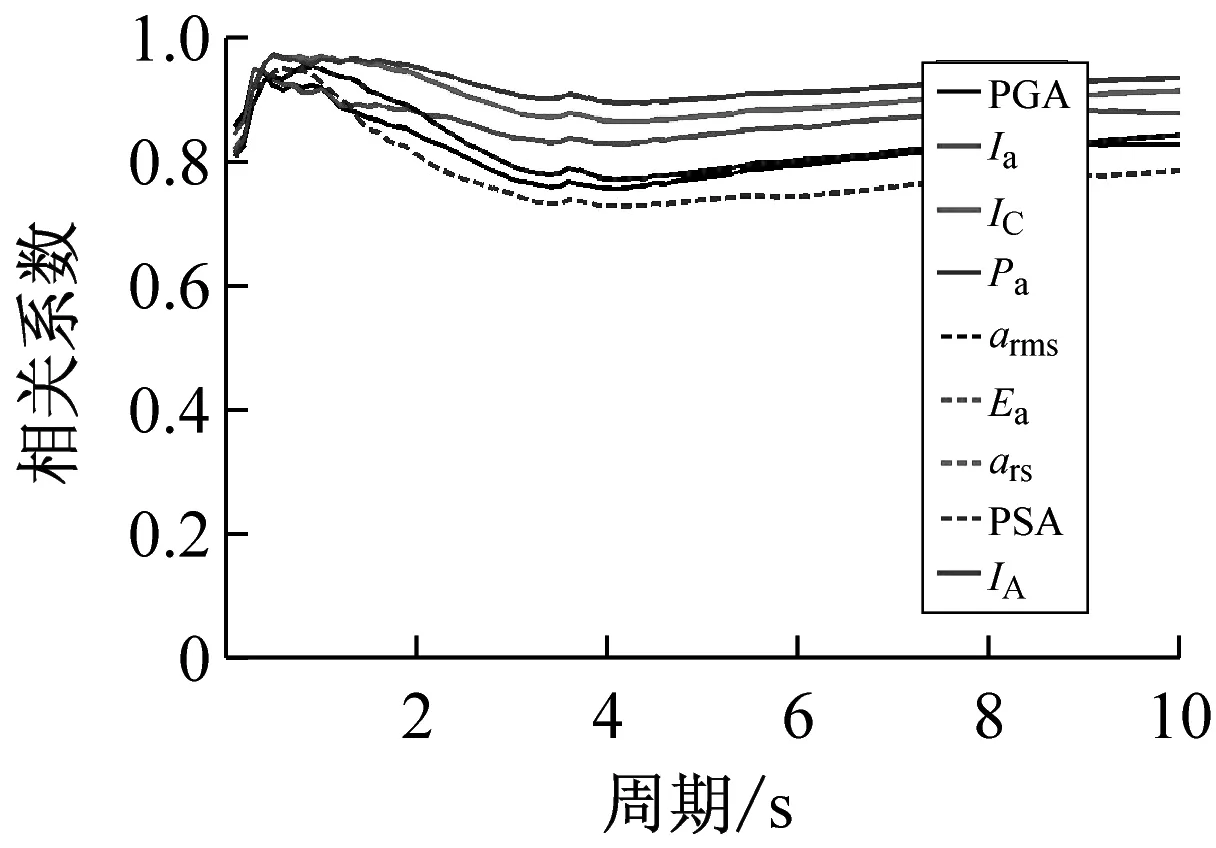
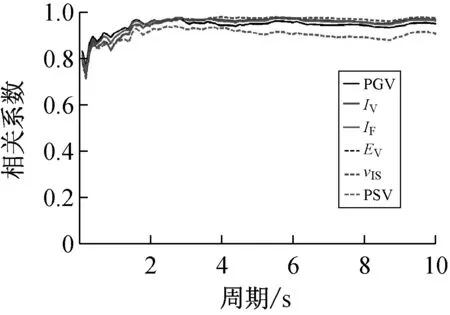
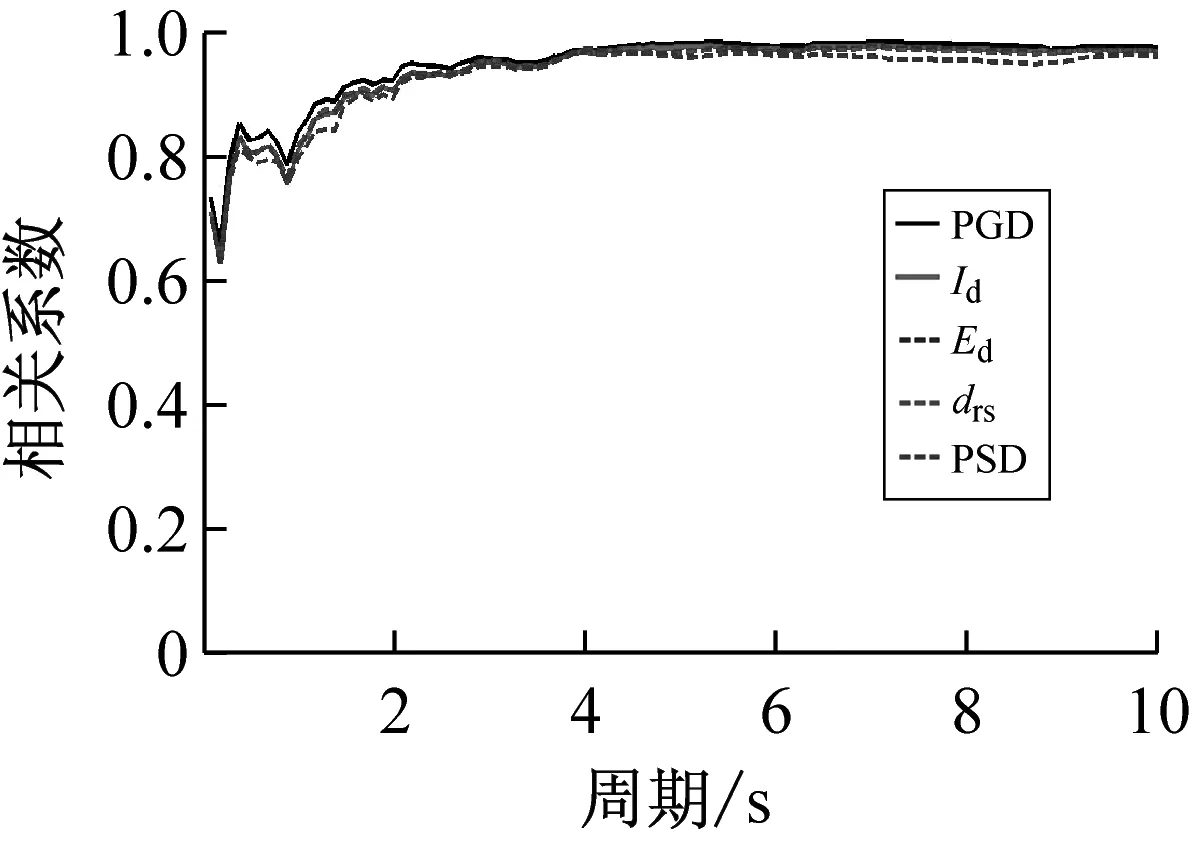
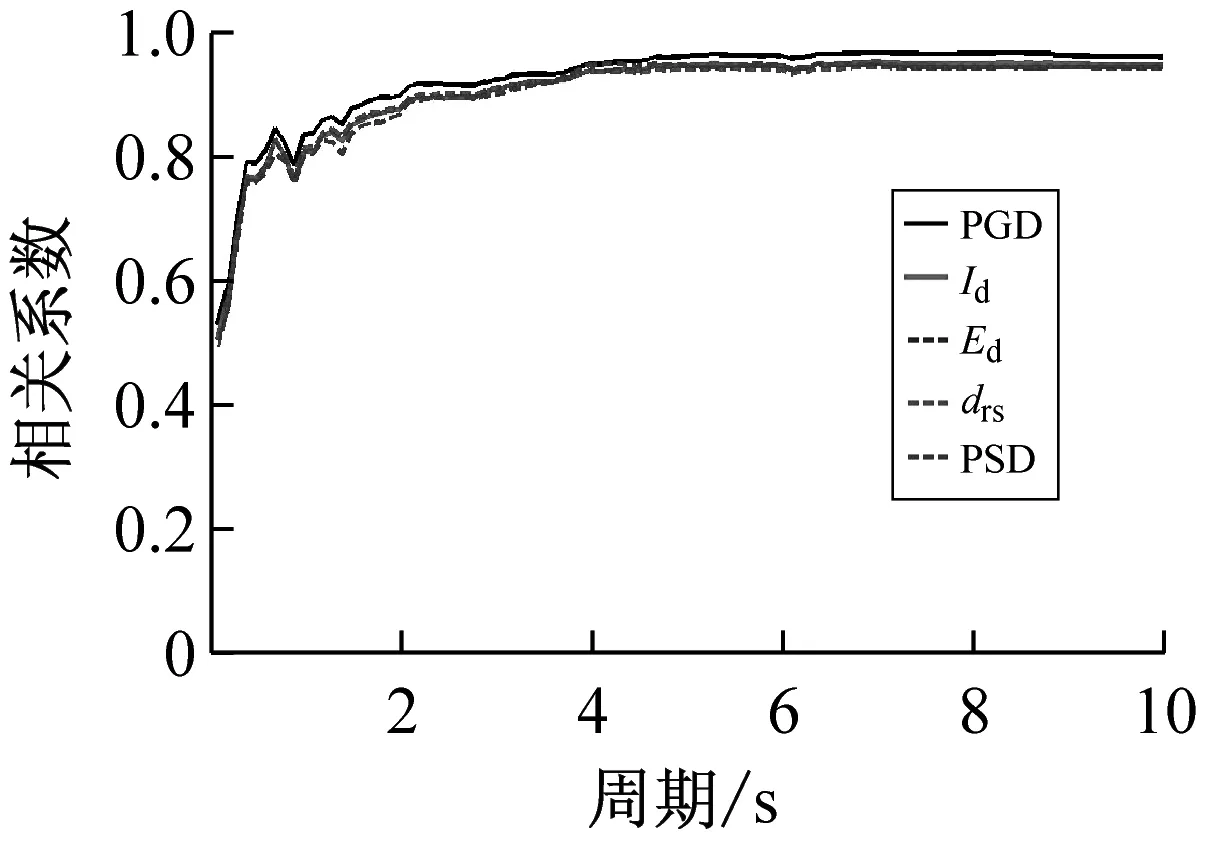
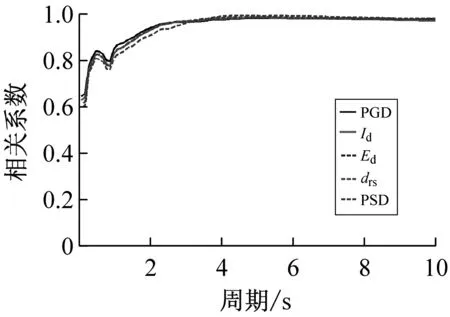
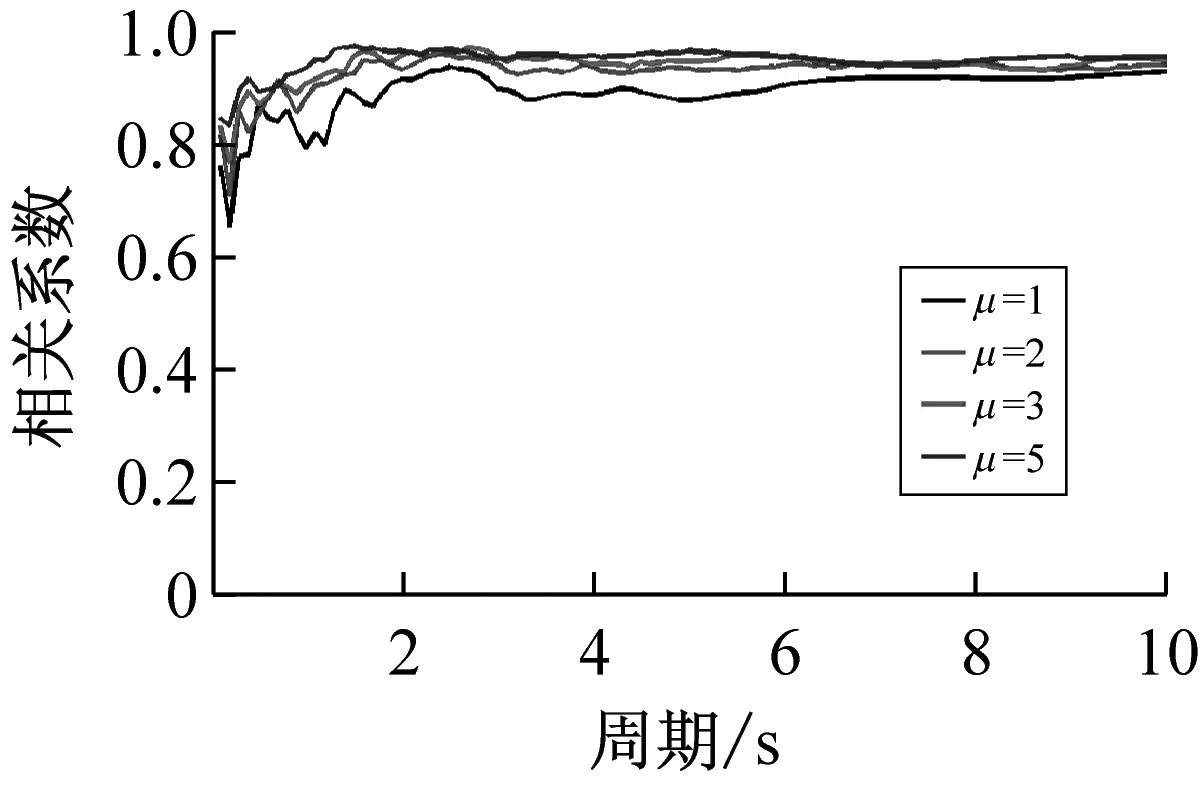
按上述方法计算得到40条远场长周期地震动的各强度指标与最大地震响应间的相关系数，如表1所示。限于篇幅，仅列出代表性周期点0.5 s、1.5 s、3.0 s与6.0 s情况下各强度指标与最大位移响应的相关系数计算结果，如表3所示。图1～图3分别为延性系数为3时加速度型强度指标、速度型强度指标与位移型强度指标和5类结构最大地震响应间的相关性。图4为不同延性系数下三类代表性强度指标PGA、PGV、PGD与最大地震响应间的相关性。

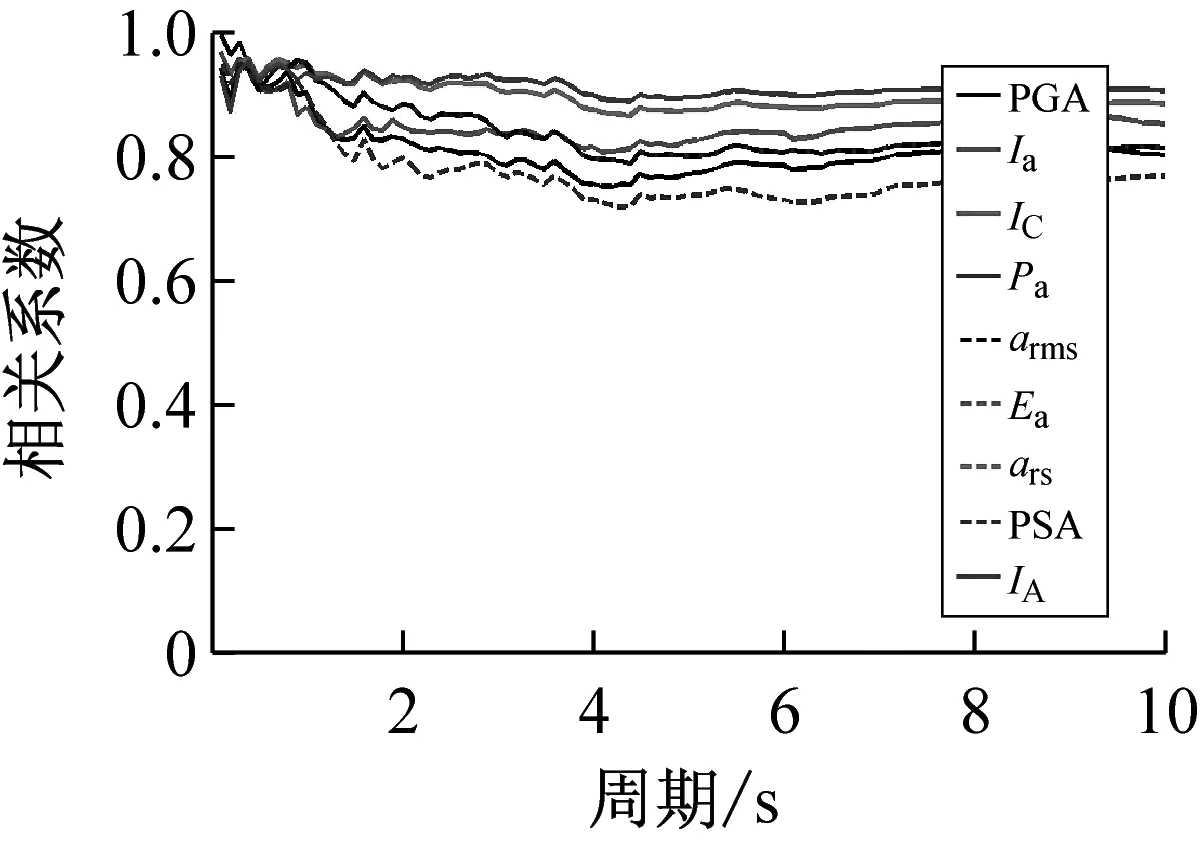
(a) 最大加速度响应

(b)最大速度响应

(c)最大位移响应

(d)最大输入能

(e)最大滞回耗能

(a) 最大加速度响应

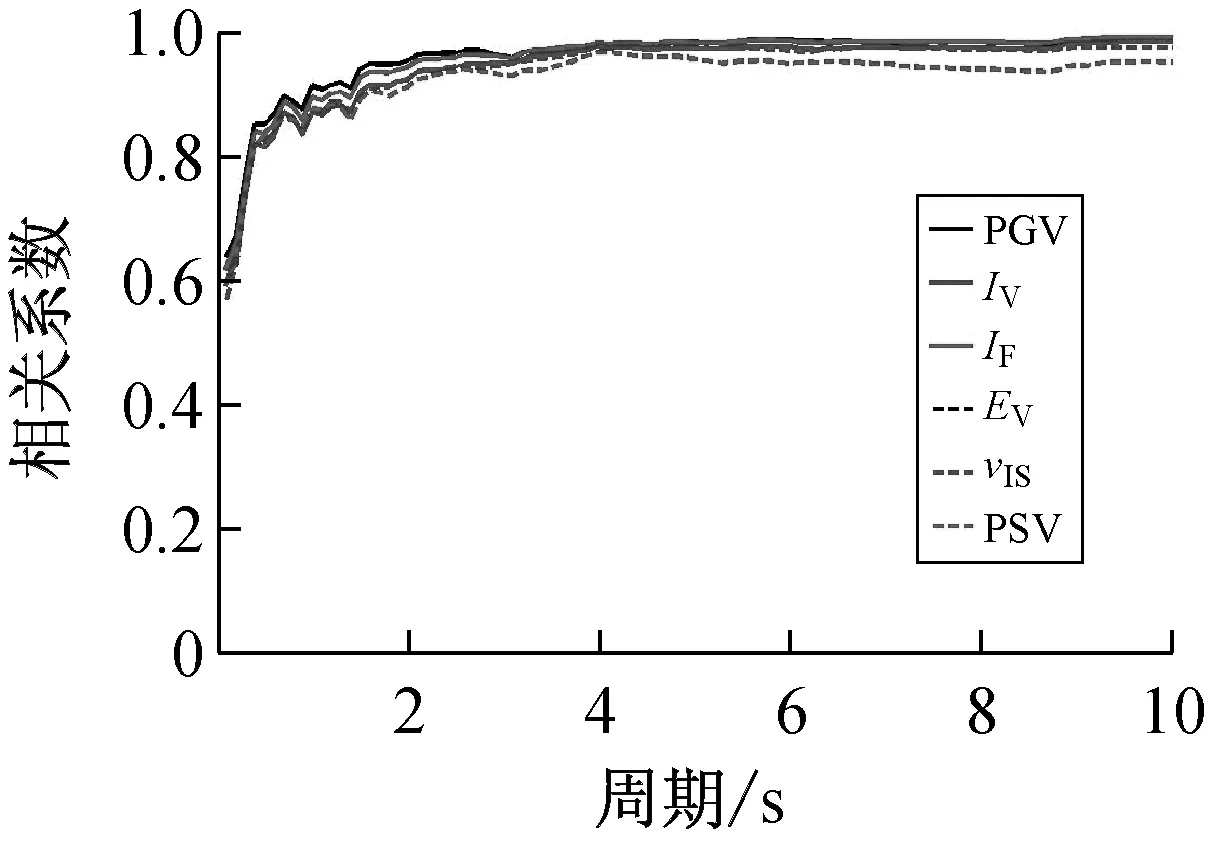
(b)最大速度响应

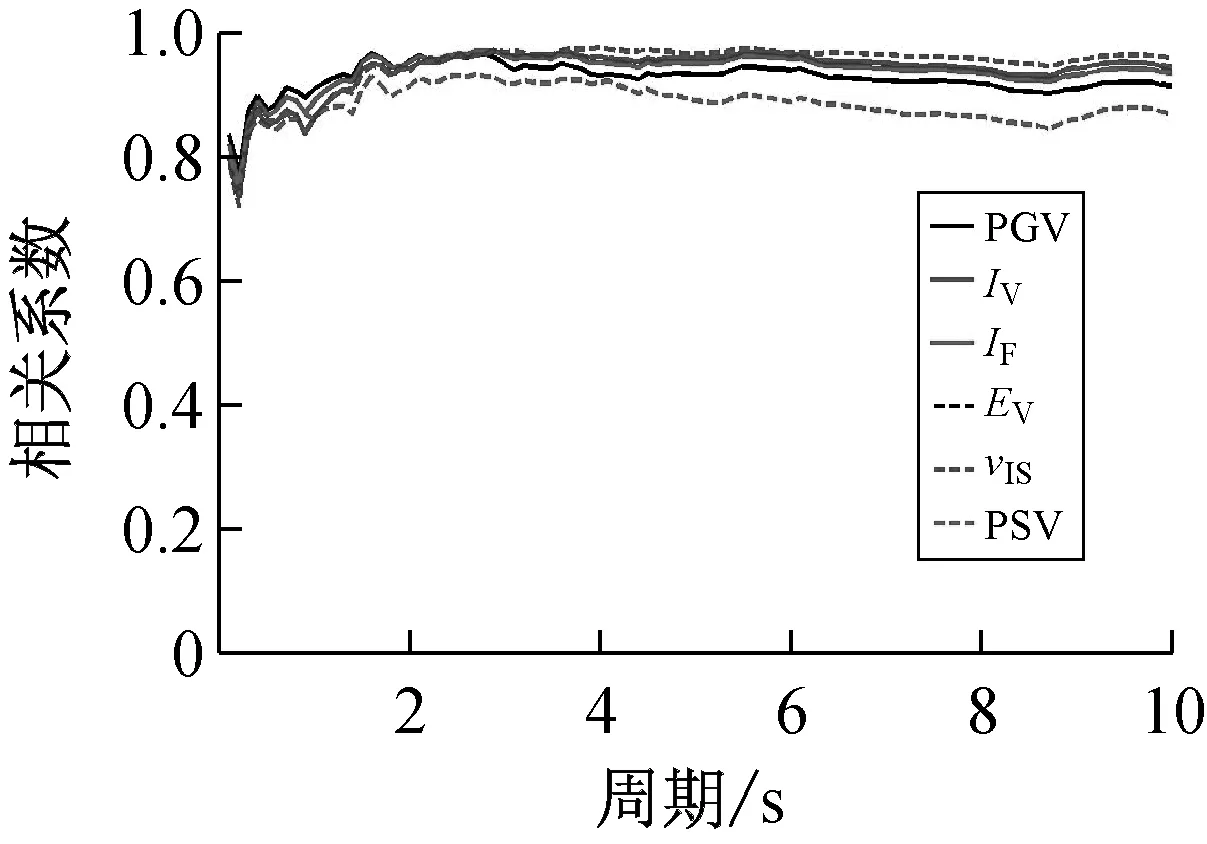
(c)最大位移响应

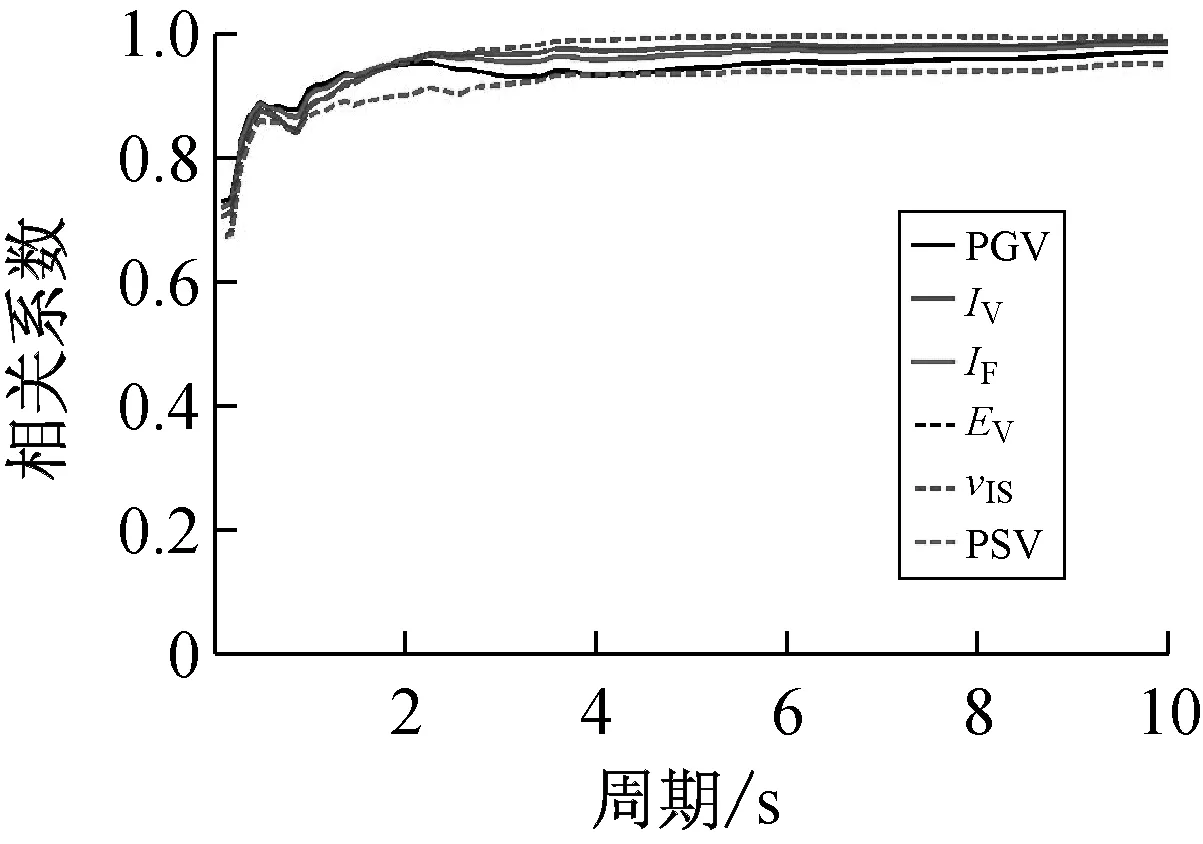
(d)最大输入能

(e)最大滞回耗能

Tab.3Calculationresultsofcorrelationcoefficientofintensityindexandmaximumdisplacementresponseforfar-fieldlong-periodgroundmotion

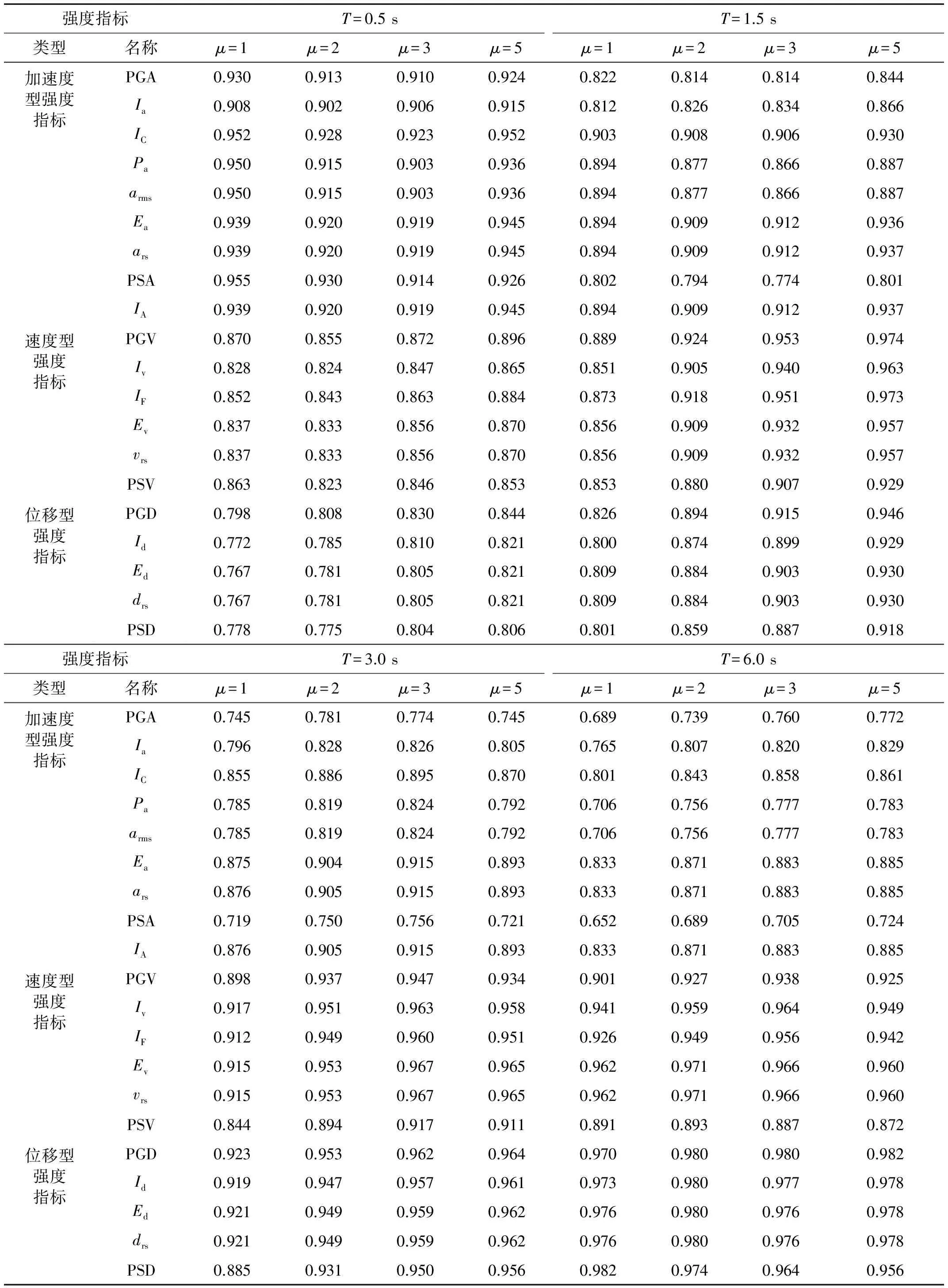
强度指标T=0．5sT=1．5s类型名称μ=1μ=2μ=3μ=5μ=1μ=2μ=3μ=5加速度型强度指标速度型强度指标位移型强度指标PGAIaICPaarmsEaarsPSAIAPGVIvIFEvvrsPSVPGDIdEddrsPSD0．9300．9130．9100．9240．8220．8140．8140．8440．9080．9020．9060．9150．8120．8260．8340．8660．9520．9280．9230．9520．9030．9080．9060．9300．9500．9150．9030．9360．8940．8770．8660．8870．9500．9150．9030．9360．8940．8770．8660．8870．9390．9200．9190．9450．8940．9090．9120．9360．9390．9200．9190．9450．8940．9090．9120．9370．9550．9300．9140．9260．8020．7940．7740．8010．9390．9200．9190．9450．8940．9090．9120．9370．8700．8550．8720．8960．8890．9240．9530．9740．8280．8240．8470．8650．8510．9050．9400．9630．8520．8430．8630．8840．8730．9180．9510．9730．8370．8330．8560．8700．8560．9090．9320．9570．8370．8330．8560．8700．8560．9090．9320．9570．8630．8230．8460．8530．8530．8800．9070．9290．7980．8080．8300．8440．8260．8940．9150．9460．7720．7850．8100．8210．8000．8740．8990．9290．7670．7810．8050．8210．8090．8840．9030．9300．7670．7810．8050．8210．8090．8840．9030．9300．7780．7750．8040．8060．8010．8590．8870．918强度指标T=3．0sT=6．0s类型名称μ=1μ=2μ=3μ=5μ=1μ=2μ=3μ=5加速度型强度指标速度型强度指标位移型强度指标PGAIaICPaarmsEaarsPSAIAPGVIvIFEvvrsPSVPGDIdEddrsPSD0．7450．7810．7740．7450．6890．7390．7600．7720．7960．8280．8260．8050．7650．8070．8200．8290．8550．8860．8950．8700．8010．8430．8580．8610．7850．8190．8240．7920．7060．7560．7770．7830．7850．8190．8240．7920．7060．7560．7770．7830．8750．9040．9150．8930．8330．8710．8830．8850．8760．9050．9150．8930．8330．8710．8830．8850．7190．7500．7560．7210．6520．6890．7050．7240．8760．9050．9150．8930．8330．8710．8830．8850．8980．9370．9470．9340．9010．9270．9380．9250．9170．9510．9630．9580．9410．9590．9640．9490．9120．9490．9600．9510．9260．9490．9560．9420．9150．9530．9670．9650．9620．9710．9660．9600．9150．9530．9670．9650．9620．9710．9660．9600．8440．8940．9170．9110．8910．8930．8870．8720．9230．9530．9620．9640．9700．9800．9800．9820．9190．9470．9570．9610．9730．9800．9770．9780．9210．9490．9590．9620．9760．9800．9760．9780．9210．9490．9590．9620．9760．9800．9760．9780．8850．9310．9500．9560．9820．9740．9640．956

(a) 最大加速度响应

(b)最大速度响应

(c)最大位移响应

(d)最大输入能

(e)最大滞回耗能

(a)PGA与最大加速度响应

(b)PGV与最大加速度响应

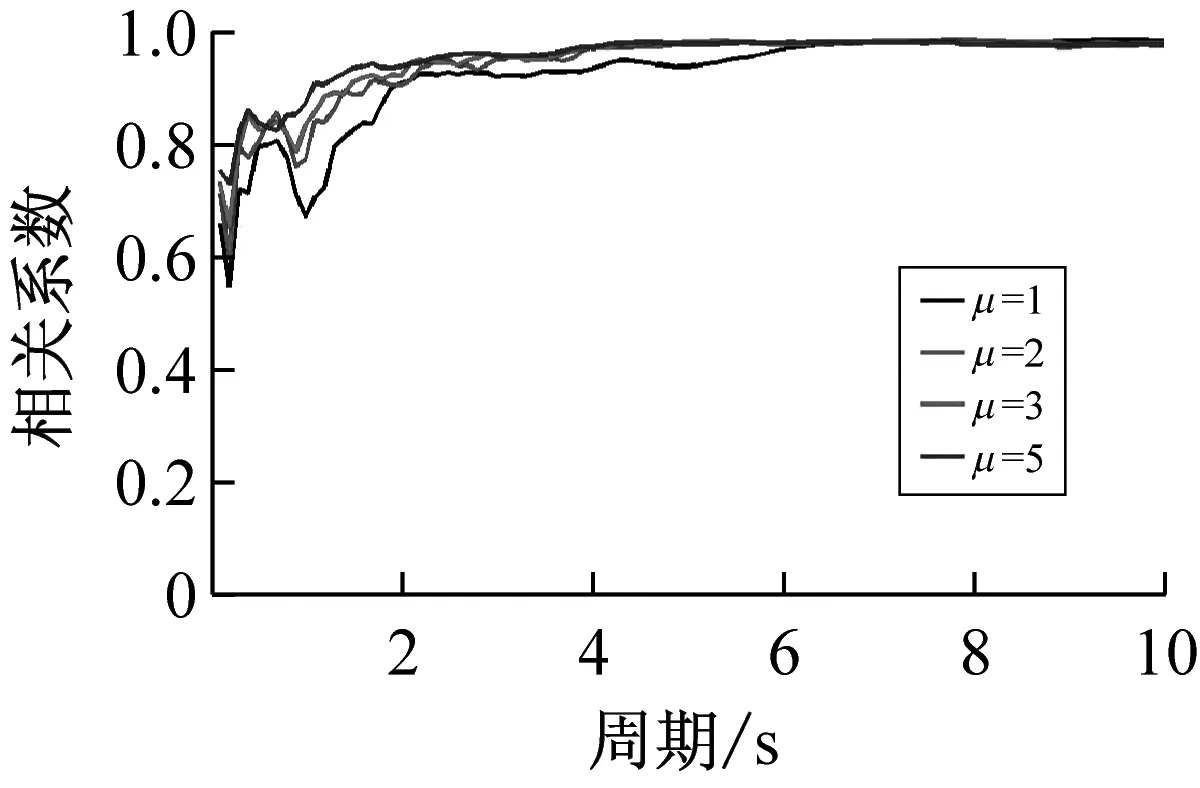
(c)PGD与最大加速度响应

(d)PGA与最大位移响应

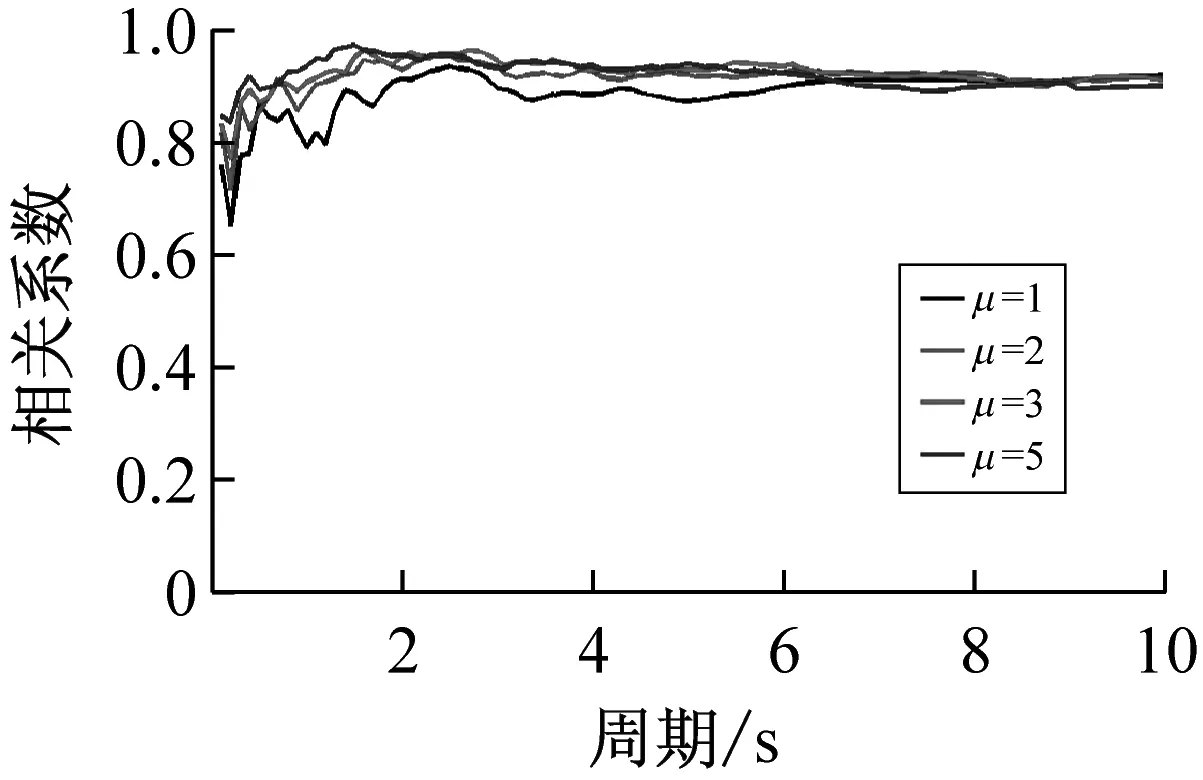
(e)PGV与最大位移响应

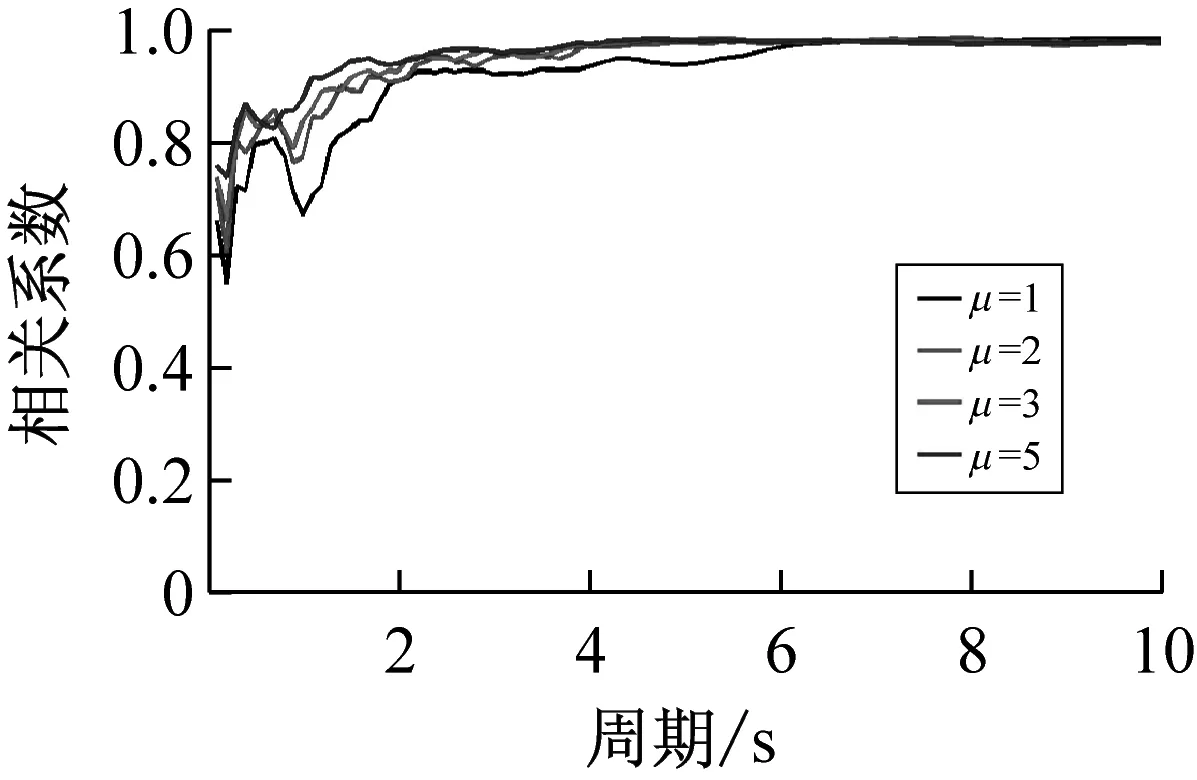
(f)PGD与最大位移响应

(g)PGA与最大输入能

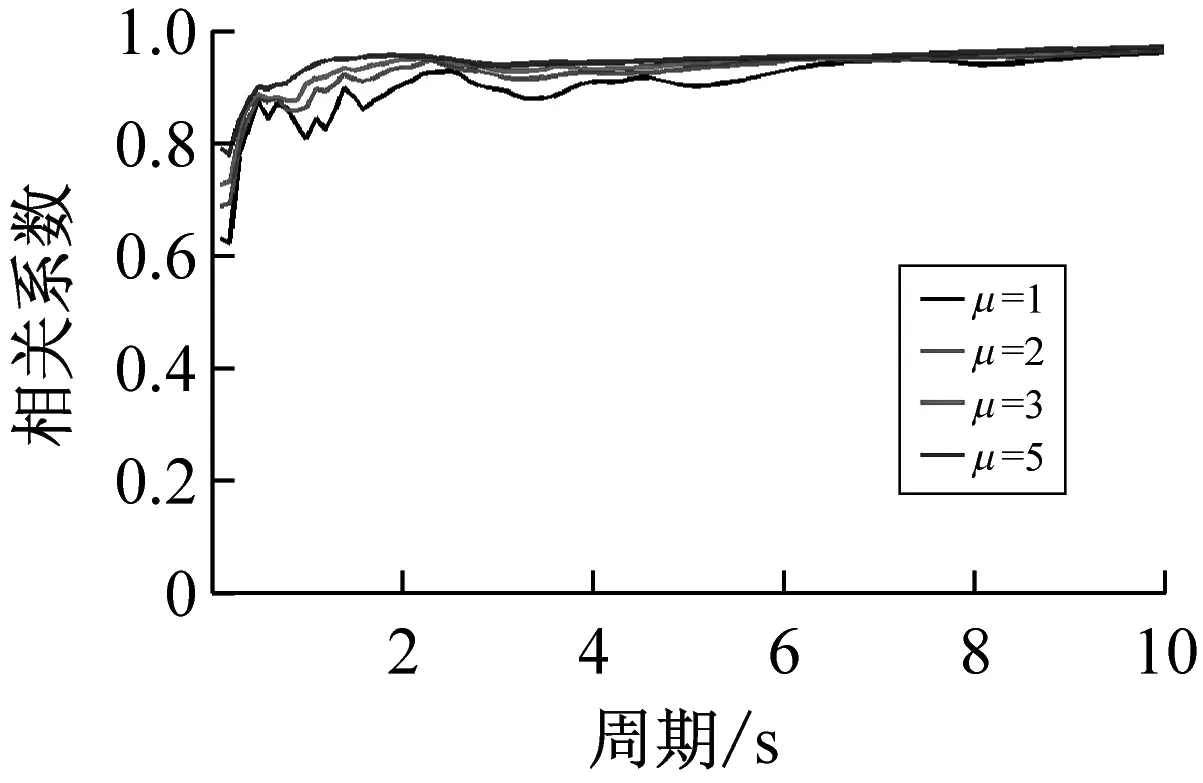
(h)PGV与最大输入能

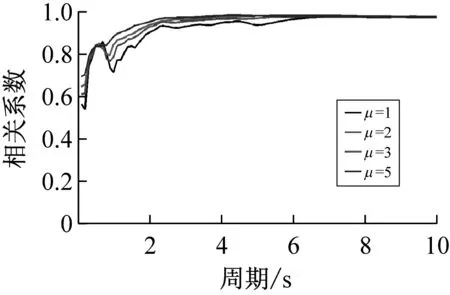
(i)PGD与最大输入能

计算结果分析表明：

(1)对于加速度型强度指标，其与最大地震响应的相关性规律具体体现在：① 延性系数对加速度型强度指标与最大地震响应的相关性受自振周期影响，在短周期范围内，相关系数随延性系数的增大而减小，在长周期范围内，相关系数随延性系数的增大而增大，而在中周期范围内，相关系数随延性系数无明显变化规律；② 加速度型强度指标与最大地震响应的相关性在短周期范围内优于中、长周期范围，且相关系数随自振周期的增大而呈减小趋势；③ 不同种类加速度型强度指标与最大地震响应的相关程度不同，其中，IC、Ea、ars、IA四种强度指标与最大地震响应的相关性一直较为稳定，而工程中常用的PGA强度指标在自振周期为6s时与弹性最大位移响应的相关系数已降至0.689，下降明显。

(2)对于速度型强度指标，其与最大地震响应的相关性规律具体体现在：① 延性系数对速度型强度指标与最大地震响应的相关性受自振周期的影响，在短周期范围内，相关系数随延性系数的增大而先减小后增大，在长周期范围内，相关系数随延性系数的增大而先增大后减小，在中周期范围内，相关系数随延性系数的增大而增大；② 在各周期范围内，速度型强度指标与最大地震响应均表现出较好的相关性，且相关系数随周期增大而增大，在中长周期范围内，相关系数普遍>0.9；③ 不同种类速度型强度指标与最大地震响应的相关程度不同，其中，在短中周期范围内，PGV与最大地震响应的相关性最好，在长周期范围内，Ev、vrs与最大地震响应的相关性最好，但总体而言，PGV与最大地震响应相关性一直较为稳定，在长周期段其相关性虽低于Ev、vrs，但相关系数亦>0.9。

(3)对于位移型强度指标，其与最大地震响应的相关性规律具体体现在：① 位移型强度指标与最大地震响应的相关性总体上随延性系数的增大而增大，规律性较强；② 位移型强度指标与最大地震响应的相关性在中长周期范围内要好于短周期范围的情况，且相关系数随自振周期的增大而增大；③ 不同位移型强度指标与最大地震响应的相关程度不同，其中，PGD与最大地震响应的相关性最稳定，在周期为6 s时，其对应的相关系数已>0.97。

综上分析可知，加速度型强度指标与最大地震响应的相关性随周期的增大而减弱，工程中通常采用的强度指标PGA不宜作为远场长周期地震动的抗震分析用强度指标；速度与位移型强度指标与最大地震响应的相关性随周期的增大而增强，且速度型强度指标PGV和位移型强度指标PGD在各周期范围内均与最大地震响应具有较好的相关性，考虑到长周期结构对远场长周期地震动比较敏感，因此建议选用PGV或PGD作为其抗震分析用强度指标。

4 结 论

针对现阶段尚未有适用于远场长周期地震动的频谱特征周期表征参数与抗震分析用强度指标问题，基于实际远场长周期地震动记录进行了程序编制计算与统计分析工作。所得主要结论如下：

(1)远场长周期地震动不同频谱周期参数的平均值与稳定性不同，其中，Hilbert边际谱平均周期Tmh属于平滑周期参数，既能反映地震动在主要频率范围内(0.25～20 Hz)的平均频谱特性，又具有较高的稳定性，因此初步建议选用Hilbert边际谱平均周期Tmh作为远场长周期地震动的频谱特征周期表征参数。

(2)远场长周期地震动加速度型强度指标与最大地震响应的相关性随周期增大而减弱，工程中通常采用的强度指标PGA不宜作为远场长周期地震动抗震分析用强度指标；速度与位移型强度指标与最大地震响应的相关性随周期增大而增强，且PGV和PGD在各周期范围内均与最大地震响应有较好的相关性，考虑到长周期结构对远场长周期地震动比较敏感，因此建议选用PGV或PGD作为其抗震分析用强度指标。

[1] 周福霖，崔鸿超，安部重孝，等. 东日本大地震灾害考察报告[J]. 建筑结构，2012，42(4)：1-20.

ZHOU Fulin, CUI Hongchao, ABE Shigetaka, et al. Inspection report of the disaster of the Ease Japan earthquake by Sino-Japanese joint mission[J].Buildings, 2012, 42(4):1-20.

[2] 肖从真，徐培福，杜义欣，等. 超高层建筑考虑长周期地震影响的另一种控制方法[J]. 土木工程学报，2014，47(2)：12-22.

XIAO Congzhen, XU Peifu, DU Yixin, et al. Another controlling method on long-period seismic responses for super high-rise buildings[J]. Journal of China Civil Engineering,2014，47(2):12-22.

[3] 徐龙军，谢礼立. 集集地震近断层地震动频谱特性[J]. 地震学报，2005，27(6)：656-665.

XU Longjun, XIE Lili. Characteristics of frequency content of near-fault ground motions during the Chi-Chi earthquake[J]. Acta Seismologica Sinica, 2005, 27(6): 656-665.

[4] 建筑抗震设计规范：GB 50011—2010[S]. 北京：中国建筑工业出版社, 2010.

[5] 陈清军，袁伟泽. 基于长周期地震动记录的 SDOF体系能量谱探讨[J]. 振动与冲击，2013，32(10)：36-42.

CHEN Qingjun, YUAN Weize. Energy spectrum of SDOF system based on long-period ground motion records[J]. Journal of Vibration and Shock,2013,32(10):36-42.

[6] 王博，白国良，代慧娟. 典型地震动作用下长周期单自由度体系地震反应分析[J].振动与冲击，2013，32(15)：190-196.

WANG Bo, BAI Guoliang, DAI Huijuan. Seismic response analysis of long-period SDOF system under typical ground motions[J]. Journal of Vibration and Shock,2013,32(15): 190-196.

[7] 杜东升，王曙光，刘伟庆，等. 长周期地震动影响因素及频谱参数研究[J]. 建筑结构学报，2014，35(增刊1)：1-8.

DU Dongsheng, WANG Shuguang, LIU Weiqing, et al. Study on affecting factors and spectral parameters of long period ground motions[J]. Journal of Building Structures,2014,35(Sup1):1-8.

[8] Applied Technology Council(ATC). Tentative provisions for the development of seismic regulations for buildings[C]. ATC-06.Redwood City，CA，1978:1-52.

[9] YANG D X, WANG W. Nonlocal period parameters of frequency content characterization for near-fault ground motions[J]. Earthquake Engineering and Structural Dynamics, 2012, 41(14): DOI 10.1002/eqe.2157.

[10] NEWMARK N M, HALL W J. Earthquake spectra and design[D]. Berkeley, CA: Earthquake Engineering Research Institute, 1982.

[11] RATHJE E M, FARAJ F, RUSSELL S, et al. Empirical relationship for frequency content parameters of earthquake ground motions[J]. Earthquake Spectra, 2004, 20(1):119-144.

[12] RATHJE E M, ABRAHAMON N A, BRAY J D. Simplified frequency content estimates of earthquake ground motions[J]. Journal of Geotechnical Engineering, 1998, 124(2):150-159.

[13] 王伟. 近断层地震动的频谱特性与能量谱分析[D]. 大连：大连理工大学，2010.

[14] 陆新征，叶列平，缪志伟，等.建筑抗震弹塑性分析—原理、模型与在ABAQUS，MSC.MARC和SAP2000上的实践[M].北京：中国建筑工程出版社，2009.

[15] 陈波. 结构非线性动力分析中地震动记录的选择和调整方法研究[D]. 北京：中国地震局地球物理研究所，2013.

[16] 陈健云，李静，韩进财，等. 地震动强度指标与框架结构响应的相关性研究[J]. 振动与冲击，2017，36(3)：105-112.

CHEN Jianyun, LI Jing, HAN Jincai, et al. Correlation between ground motion intensity indexes and seismic responses of frame structures[J]. Journal of Vibration and Shock, 2017, 36(3): 105-112.

[17] ARIAS A. A measure of earthquake intensity[M]//Seismic Design for Nuclear Power Plants. Cambridge, MA: MIT Press, 1970.

[18] RIDDELL R, GARCIA E J. Hysteretic energy spectrum and damage control[J]. Earthquake Engineering and Structure Dynamics, 2001, 30(12):1791-1816.

[19] HOUSNER G W. Measures of severity of earthquake ground shaking[C]//Proceedings of the U. S. National Conference on Earthquake Engineering. Ann Arbor: EERI, 1975.

[20] HONSNER G W, JENNINGS P C. Generation of artificial earthquakes[J]. Journal of the Engineering Mechanics Divison, 1964, 90(EM1):113-150.

[21] PARK Y J, ANG A H S, WEN Y K. Seismic damage analysis of reinforced concrete buildings[J]. Journal of Structural Engineering, 1985, 111(4):740-757.

[22] NAU J M, HALL W J. An evaluation of scaling methods for earthquake response spectra[D]. Urbana: University of Illinois.

[23] FAJFAR P, VIDIC T, FISCHINGER M. A measure dynamics of earthquake motion capacity to damage medium-period structures[J]. Soil Dynamics and Earthquake Engineering, 9(5):236-242.

[24] 郝敏，谢礼力，徐龙军. 关于地震烈度物理标准研究的若干思考[J]. 地震学报，2005,27(2)：230-234.

HAO Min, XIE Lili, XU Longjun. Some considerations on the physical measure of seismic intensity[J]. Acta Seismologica Sinica, 2005, 27(2): 230-234.

[25] RAFAEL R. On ground motion intensity indices[J]. Earthquake Spectra, 2007, 23(1):147-173.

[26] YANG D X, PAN J W, LI G. Non-structure-specific intensity measure parameters and characteristic period of near-fault ground motions[J]. Earthquake Engineering and Structural Dynamics, 2009, 38:1257-1280.