基于最小二乘支持向量机的压电作动器迟滞非线性建模及参数辨识

钱 承 胡红生

嘉兴学院机电工程学院，嘉兴，314001

0 引言

压电作动器以压电智能材料为主要材料，具有结构紧凑、作动力大、刚性高、位移分辨率高、频率响应快、控制驱动简单等优点，目前压电微位移器件已得到广泛的研究和应用[1-3]。但压电材料同时也存在着固有缺陷，如压电陶瓷材料的迟滞特性、输入输出的非线性特性、蠕变特性等[4-5]。这些固有特性的存在使得压电作动器在实际应用中重复性和控制精度降低，实时瞬态响应也相应变慢，这会使得压电作动器在工业应用中的推广具有一定难度。特别是压电材料的迟滞特性，该特性使得控制变得十分困难。

目前国内外学者已对压电材料的迟滞特性开展了广泛研究，取得了一定的成果并进行了相关的应用，主要涉及压电材料迟滞模型的理论研究或采用智能算法来建立压电非线性仿真模型以指导应用。尤其在迟滞模型方面，截至目前已形成了多种常用模型，分别为Preisach模型[6-7]、Maxwell模型[8]、Dahl模型[9]、Bouc-Wen模型[10-11]等,其中，Preisach模型及其改进形式已被广泛应用。文献[12]基于径向基神经网络法来构建迟滞非线性模型，并进行了补偿控制，得到了很好的跟踪控制性能。文献[13]提出了基于模糊控制系统的建模方法，并通过所建立的逆模型进行前馈迟滞补偿控制，在频率50 Hz和100 Hz下明显减小了迟滞特性，且该建模方法简单,可应用于实时在线建模。文献[14]为取得压电作动器的跟踪精度，在一阶回转曲线的基础上采用了双输入的Preisach迟滞模型来预测耦合迟滞特性，通过实验对比单输入的Preisach迟滞模型的控制情况，结果表明双输入的Preisach迟滞模型具有更好的性能。文献[15]将压电作动器应用于显微操纵器，采用Preisach迟滞理论建立压电作动器的迟滞模型，并提出利用前馈非线性PID控制法结合Preisach迟滞补偿法来控制定位精度，最终通过实验验证了该机构控制性能满足设计要求。

对于Preisach迟滞理论的建模，其计算的难点为求取各个迟滞单元的加权系数。通过一系列的一阶回转曲线来求取迟滞单元加权系数的方法被证实为一种求解精度较高的方法，但该方法的缺点是需要通过实验获取大量的一阶回转曲线，要使所有的实验均达到很高的精度，则具有一定的难度。针对上述问题，研究人员采用人工智能技术来计算迟滞单元加权系数[12,16-18]，通过测试一定量的一阶回转曲线，根据一阶回转曲线建立人工智能模型从而建立更详细的迟滞模型，这将减少大量测试带来的时间及误差，但辨识精度、效率仍依赖于实验样本，且模型参数随外部输入信号变化的自适应性较差，拟合的数学曲线在实际工程应用中无法精确模拟压电迟滞特性，故误差难以控制。

最小二乘支持向量机(least squares support vector machines，LS-SVM)将传统支持向量机(SVM)中的不等式约束改成等式约束，是SVM的一种改进形式。LS-SVM将二次规划问题转化为线性方程组求解问题，提高了求解速度及收敛精度[19-20]。考虑到LS-SVM的诸多优点，本文基于Preisach离散迟滞模型，在实验的基础上得到压电作动器的一阶回转曲线，通过一阶回转曲线求取迟滞单元加权值并应用LS-SVM法建立所需的迟滞模型，引入遗传算法对模型参数进行寻优得到最精确的模型，最后通过仿真对比分析，验证了本文方法的可行性。

1 迟滞模型建立理论

1.1 Preisach迟滞模型理论

典型的Preisach迟滞模型[21-22]通过对迟滞因子的双重积分来计算模型的输出，其计算表达式如下：

f(t)=∬α≤βμ(α,β)γα,β(u(t))dαdβ

(1)

式中，α、β分别为迟滞单元的下阈值和上阈值；μ(α,β)为迟滞单元的加权函数；u(t)为迟滞模型的输入；γα, β(u(t))为迟滞单元的值。

迟滞单元计算原理如图1所示。对于图1所示的迟滞单元模型，也可将其表述在Preisach平面内，该平面由α、β为横纵坐标且β≥α的三角形区域构成，如图2所示。

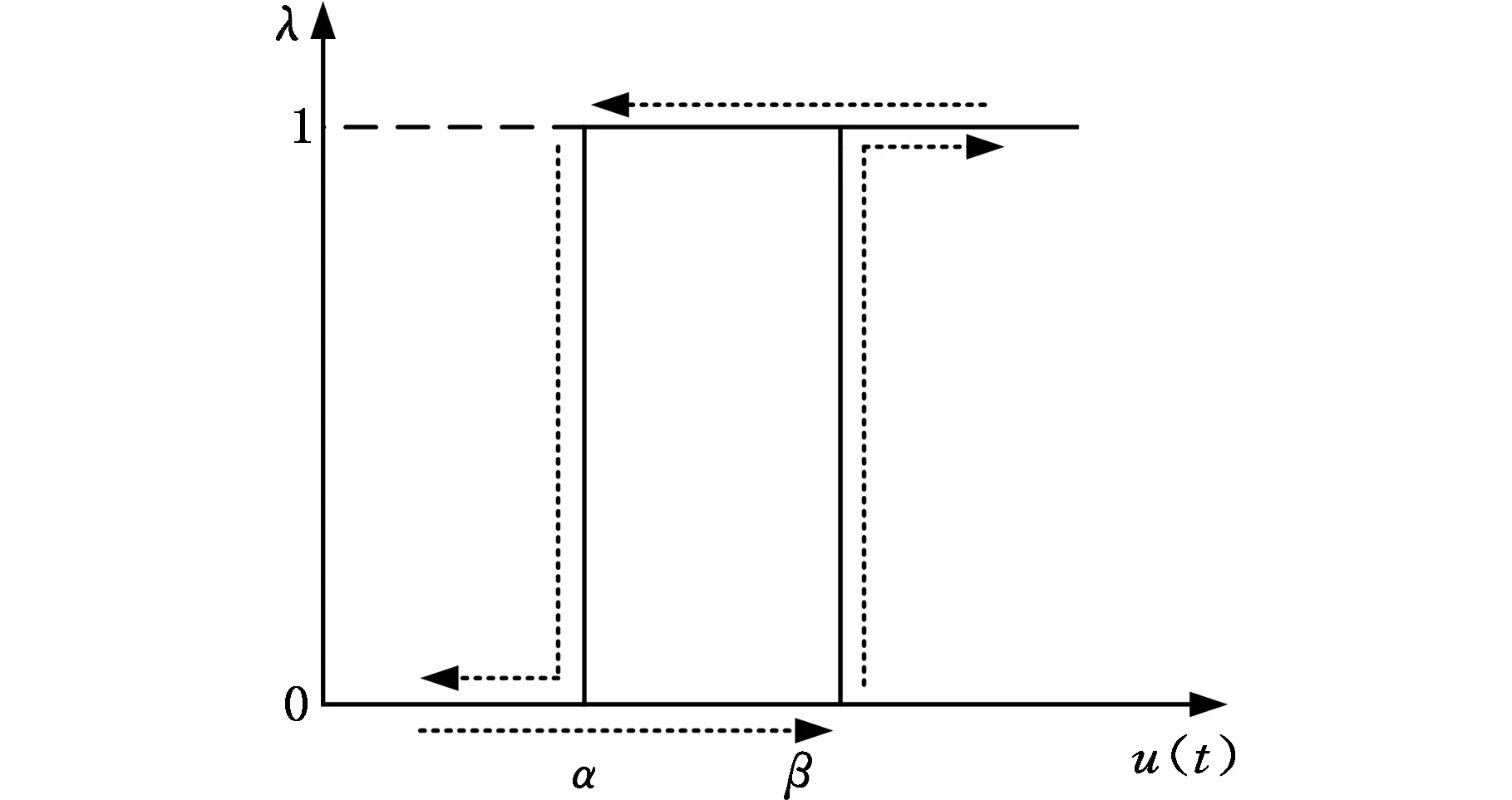
图1 迟滞单元计算原理Fig.1 Calculation principle of hysteresis unit

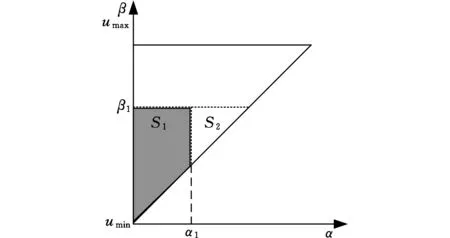
图2 迟滞计算模型的α-β平面Fig.2 α-β plane of hysteresis calculated model

由图2可以看出，在三角形区域内，加权函数μ(α,β)不为零。当输入u(t)增大或减小时会激活不同区域的迟滞单元或使激活的单元变为非激活状态，这就需要计算各个激活单元的加权函数μ(α,β)，然后根据这些加权函数求取最终的输出。常用的方法为基于一阶回转曲线来确定加权函数，且一阶回转曲线越多，模型的准确度就越高。该方法建立的迟滞模型为有限个迟滞单元的并联形式，因此其离散迟滞模型的表达式如下：

(2)

其中，μn为n×n的矩阵，矩阵元素为分割后的压电迟滞单元加权量，可通过一阶回转曲线实验获取的数据得到；γi,j(t)为判断矩阵，可判断分割后的压电迟滞单元是否激活，矩阵中元素是随时间变化的。

相应的离散迟滞模型如图3所示。

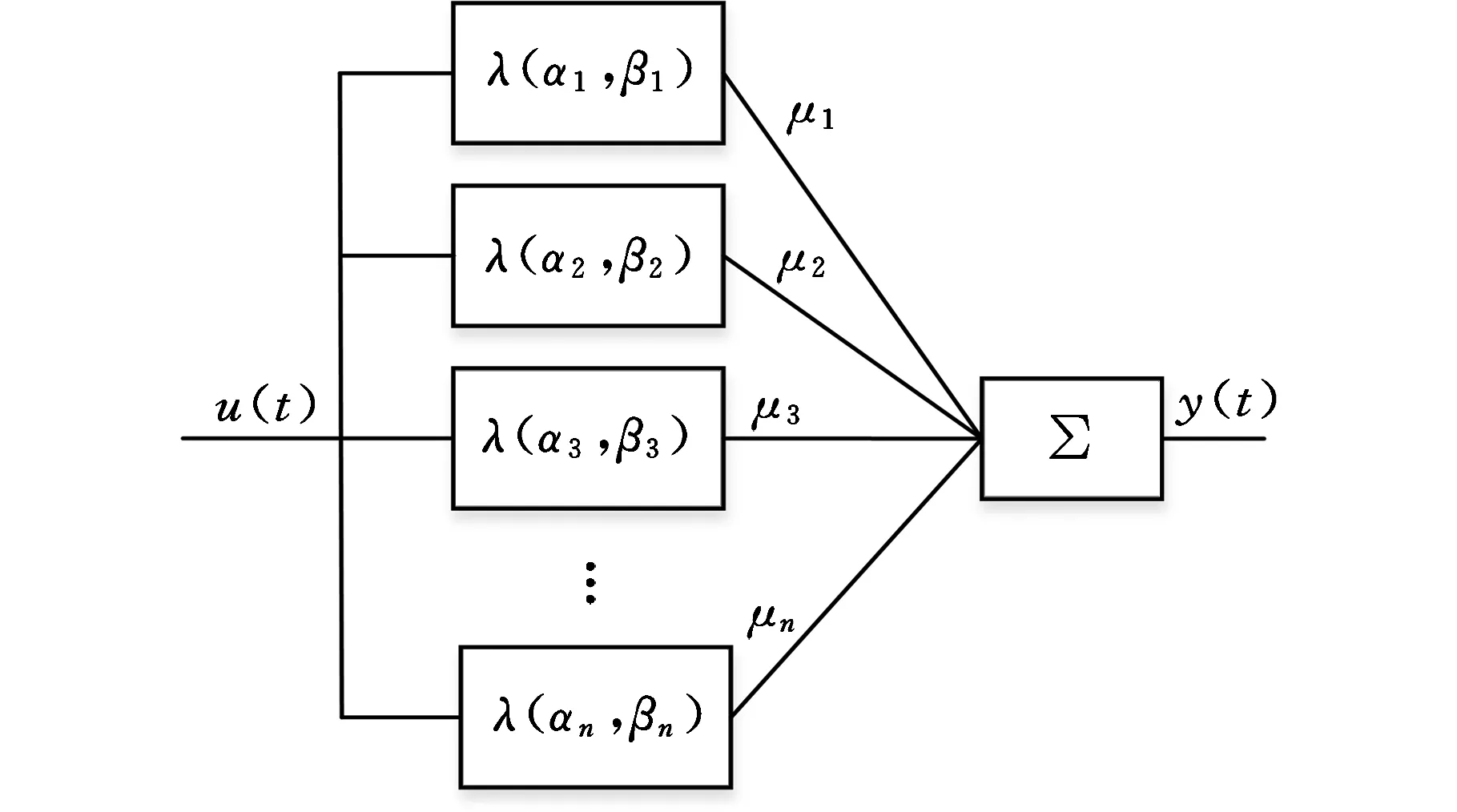
图3 离散迟滞模型并联图Fig.3 Parallel figure of discrete hysteresis model

为此，本文的研究内容主要围绕如何利用有限的一阶回转曲线快速有效地确定离散模型单个迟滞单元的加权量。

1.2 最小二乘支持向量机理论

支持向量机的核心理论是通过核函数定义的非线性变换将n维样本空间(x1,y1),(x2,y2), …(xl,yl)∈Rn,yi∈{+1,-1}(i=1,2,…,n)映射到一个高维特征空间，在此高维空间中寻找输入量与输出量之间的一种非线性关系。假设非线性映射为φ(xi)(i=1,2,…,n)，将n维样本数据(x1,y1),(x2,y2),…，(xl,yl) ∈Rn映射到高维特征空间，根据结构风险最小化原则，求解如下最优化问题：

(3)

式中，Re为经验风险值；c为惩罚因子；εi为样本误差，也称松弛变量；b为阈值；w为超平面的权值向量。

将式(3)的标准支持向量机最优化问题转化成二次规划问题，利用核函数取代高维空间中的点积运算，则可把式(3)转化成LS-SVM最优化问题，优化目标损失函数为误差εi的二次项,其关系表达式如下：

(4)

为了求解该优化问题，将约束条件改为等式约束，引入拉格朗日算子ai(i=1，2,…,n)，构造拉格朗日方程以求解此优化问题，即

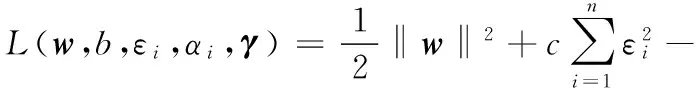
(5)

要使目标函数取得最小值，则要使拉格朗日方程中的变量w、εi、b、ai的偏导数均为0，即

(6)

通过求解该二次规划问题，可构造函数如下：

(7)

(8)

式中，K(x,xi)为核函数;σ为核参数。

基于该理论可以发现，LS-SVM法是处理非线性、小样本的回归预测计算方法。针对压电迟滞模型建立的难点正好符合非线性、小样本的特性，即可通过较少的一阶回转曲线来求解本文所需的迟滞单元加权系数。

2 压电迟滞模型参数辨识

2.1 FORC曲线的获取及初始加权函数的计算

为了将上述理论应用于压电迟滞模型的参数辨识，必须通过实验的方式获取压电作动器一定量的一阶回转曲线。压电作动器选用的型号为P-843.20(PI公司)，其主要参数如下：开环输出位移30 μm；闭环输出位移30 μm；集成反馈传感器为电阻应变片式传感器(strain gauge sensor，SGS)；开环/闭环精度0.6/0.3 μm；静态刚度27 N/μm；推力/抗拉能力800/300 N；电容3.0 μF。本文将压电驱动电压范围平均分成五等分，以20 V为间隔作为一阶回转曲线的各回转电压值(即对20 V、40 V、60 V、80 V、100 V这5个电压值进行回转)，如此便将离散迟滞模型式(2)中的n设为5，则相应的迟滞单元有n(n+1)/2个，通过这些回转曲线便能求出各个迟滞单元的加权量。

为使得到的一阶回转曲线数据准确可靠，实验进行了10个循环测量，电压加载步长为1 V，为使得到的数据是压电作动器运行在稳定状态下摒弃了前3次循环的数据，将后7个循环的数据进行平均计算，得到一阶回转曲线如图4所示。

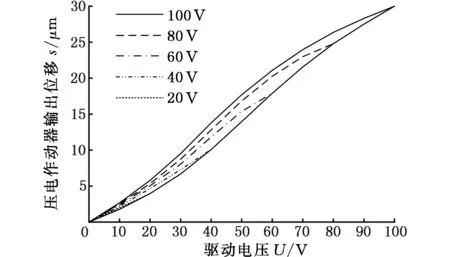
图4 一阶回转曲线Fig.4 First order reversed curves

根据该一阶回转曲线计算本文所需的初始加权值μ6：

(9)

该初始加权值是将迟滞模型在α-β平面内划分为15个迟滞单元计算所得，为了消除Preisach迟滞模型固有的迟滞特性，将该初始加权值分别除以相应迟滞单元的面积，作为该迟滞单元的平均加权值：

(10)

将式(1)转换为平均加权值和迟滞单元面积的乘积形式，即

(11)

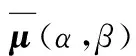
2.2 基于LS-SVM迟滞模型建立

将LS-SVM理论应用于迟滞模型，将上述划分后相应迟滞区域的形心在α-β平面内的坐标作为模型的输入，计算所得的平均加权系数则为模型的输出进行训练。对于训练模型，选择核函数为高斯径向基核函数，而惩罚因子c和核参数σ的选取对训练模型准确率具有较大的影响，因此必须在模型训练的过程中进行寻优。本文采用遗传算法对参数进行优化，其步骤如下：①选定训练样本和校验样本，设定惩罚因子c和核参数σ的区间(0,100)和(0,10)，从而产生LS-SVM参数初始群体；②设定交叉概率为0.6，变异概率为0.2，群体规模为30，进化代数为300；③进行训练得出优化后的惩罚因子c和核参数σ。

选定遗传算法的适应度函数：

(12)

式中，yi为期望输出;f(xi)为实际输出;k为一很小的正数，其作用是防止分母为零的情况出现，此处取值为10-3。

为了最优化模型，选定评价指标，定义误差函数为

(13)

初始交叉概率和初始变异概率分别由下式确定：

(14)

(15)

式中，f′为交叉两个体较大的适应度函数值;f为个体对应的适应度函数大小;favg为样本的平均适应度;fmax为样本个体的最大适应度。

仿真建模和计算均采用MATLAB软件。图5所示为初始参数下模型输出与实验数据的误差，可以看出，评价指标函数的值较大，不能满足模型计算要求。图6所示为引入遗传算法后经过200步迭代后的误差，可以看出，评价指标函数值大幅度减小。图7为在模型迭代稳定后评价指标函数图，可以看出，优化前后评价指标函数的值大幅度减小。

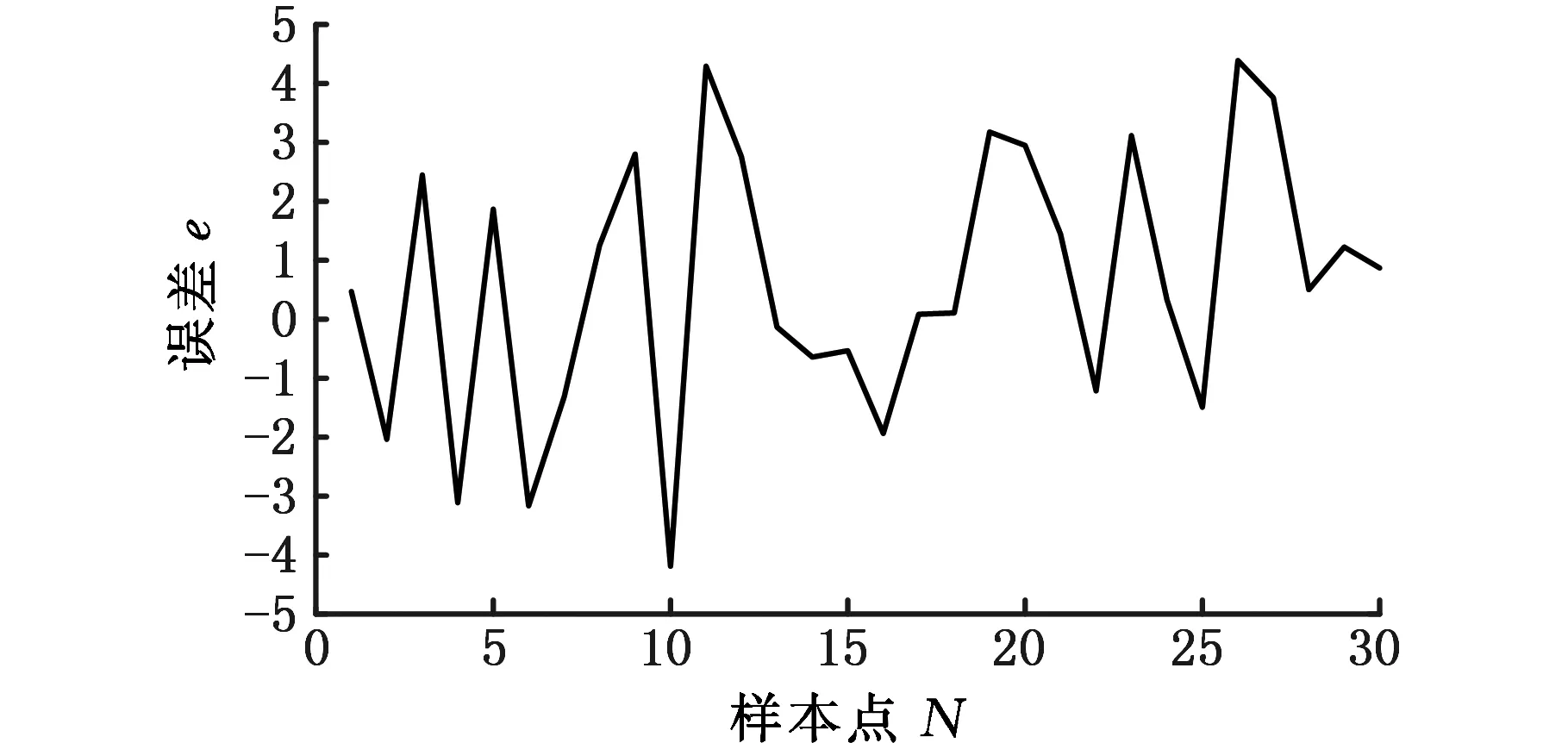
图5 初始参数样本误差Fig.5 Error under initial parameters

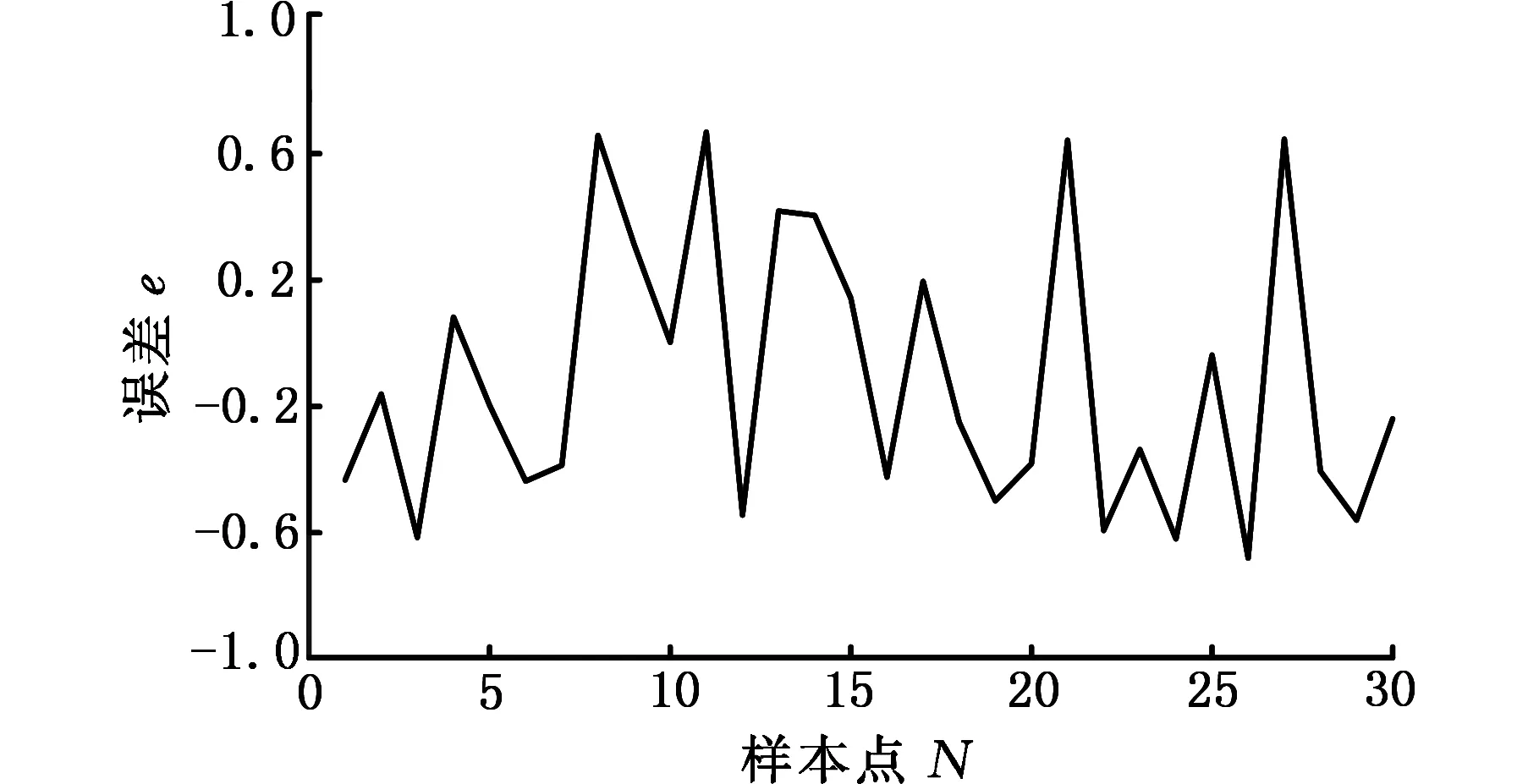
图6 迭代200步后样本误差Fig.6 Error after 200 iterations

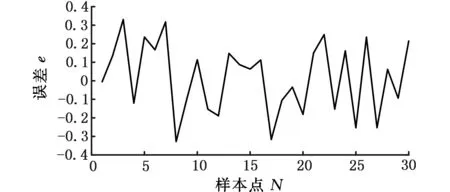
图7 迭代稳定后样本误差Fig.7 Error after stable iterations

经过计算，最终确定了惩罚因子c=13.6和核参数σ=1.4。确定了迟滞训练模型的参数，并建立了最终的计算预测模型。

将α-β平面划分为更多迟滞单元的组成形式，并将式(2)中的n设为20，即根据第一步建立的模型求取210个平均加权系数，即可通过较少的一阶回转曲线求取α-β平面内较多的平均加权系数，并根据这些平均加权系数求取更精确的压电作动器的输出。

通过上述两个步骤的计算，可得到平均加权系数的三维系数图，见图8。

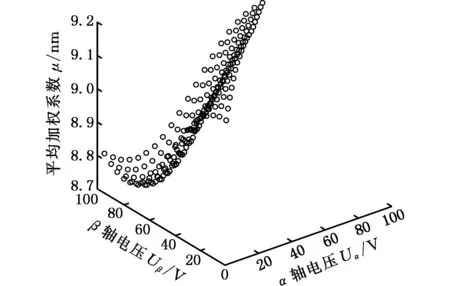
图8 平均加权系数计算值Fig.8 Calculated value of average weighted coefficients

通过平均加权系数矩阵和被激活的迟滞单元的激活面积，并利用式(11)即可求得当前压电作动器的输出值。

3 迟滞模型的验证

为验证迟滞模型的准确性，本文搭建了压电作动器迟滞实验平台，其主要组成部分包括压电作动器、压电驱动模块、传感检测模块及计算机监测软件，如图9所示。其工作原理为：控制器通过驱动模块输出电压驱动压电作动器，再由传感模块对传感器采集信号并进行检测处理，处理结果通过控制总线提供给主控模块进行计算、分析并将结果显示于电脑显示屏上，如图10所示。

1.压电驱动模块 2.微动测量台架 3.离线传感模块4.参数调整及显示模块 5.计算机 6.光学隔振平台 7.压电作动器图9 压电迟滞实验平台Fig.9 Experimental platform of piezoelectric hysteresis

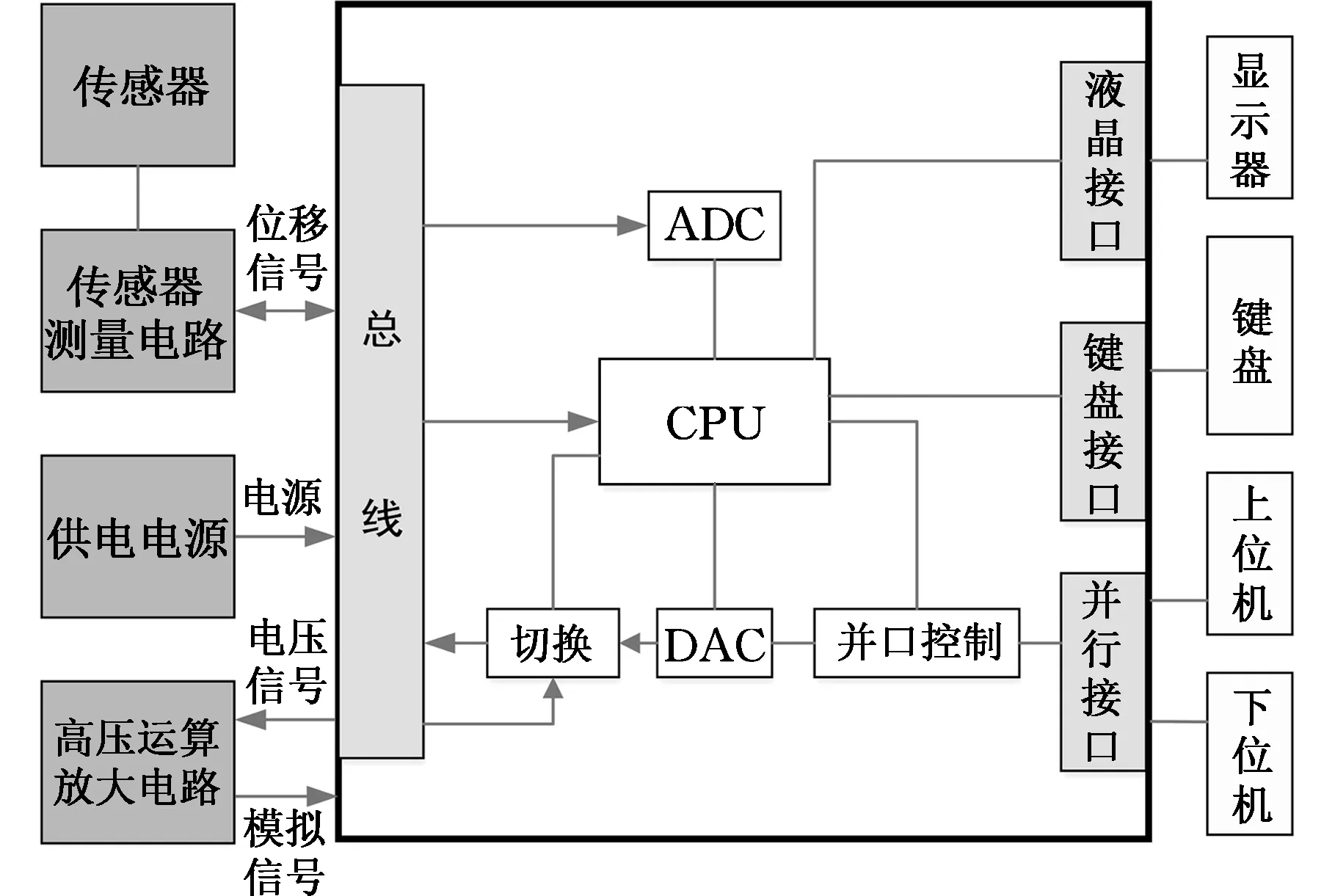
图10 实验平台工作原理Fig.10 Principle of the experimental platform

为了获得压电作动器的迟滞特性，控制器的控制模式采用开环控制。根据图10的实验平台测试原理，系统利用采集的位移信号作为输入，利用建立的迟滞模型进行计算以获取输出电压，从而完成自动加载实验。

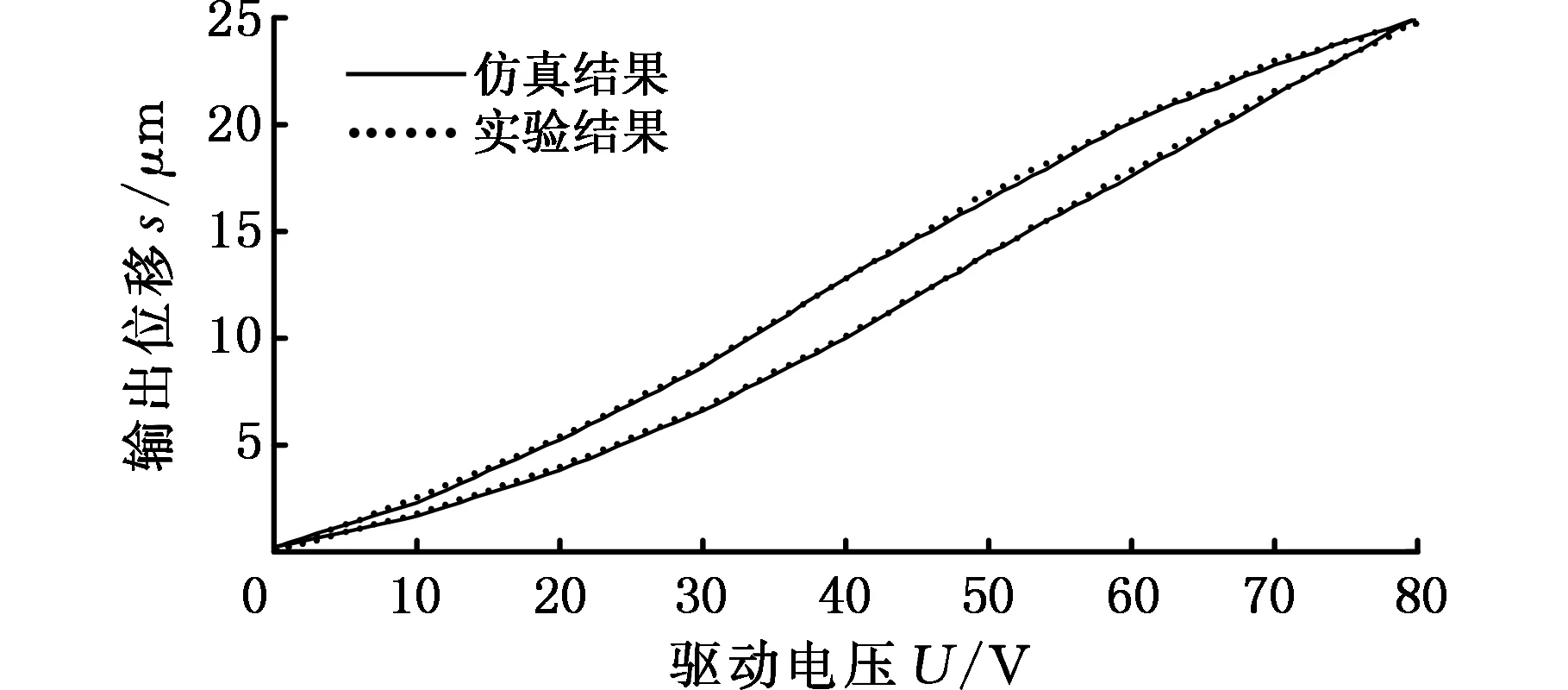
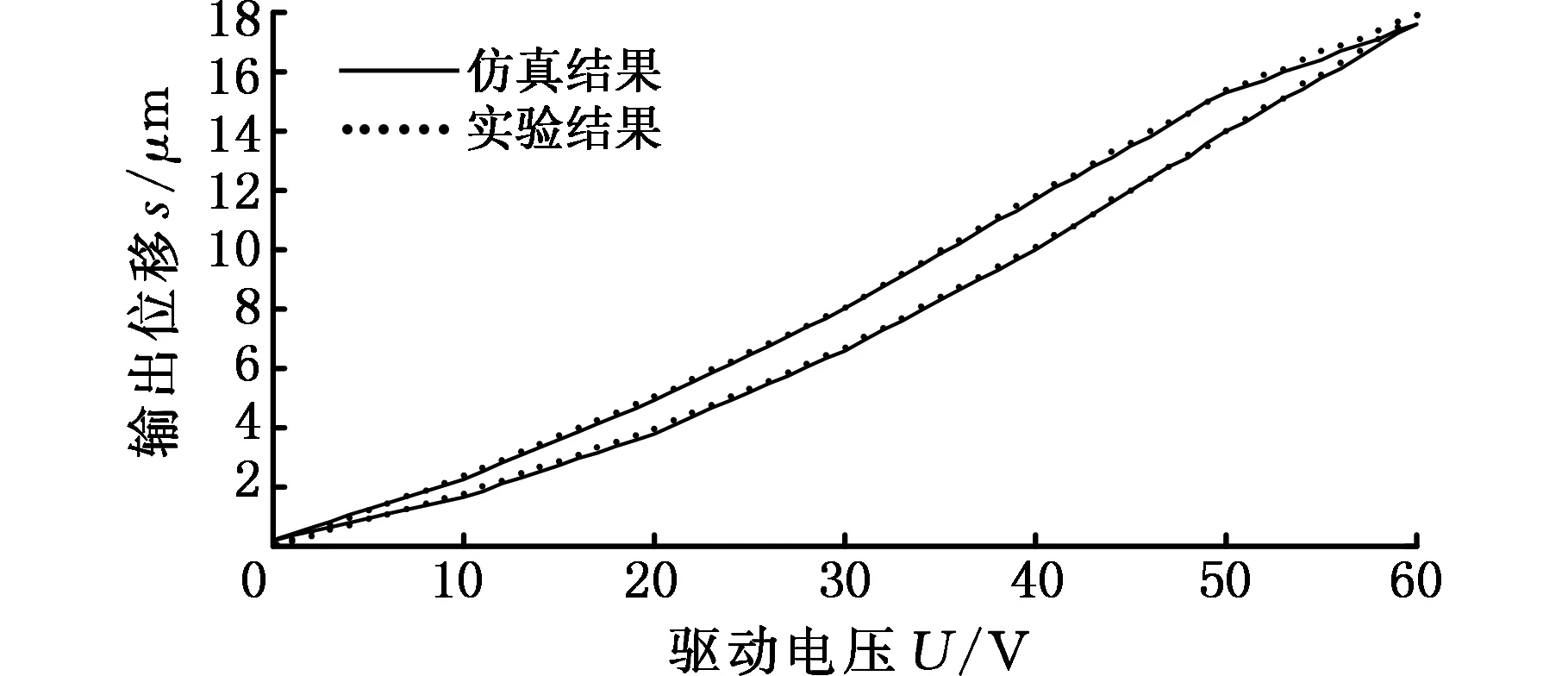
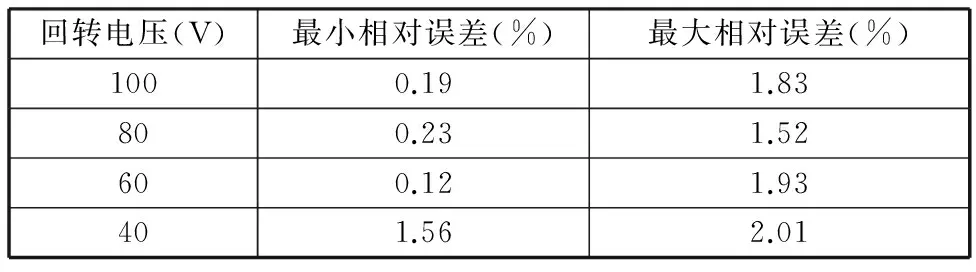
仿真和实验验证分别以40 V、60 V、80 V、100 V为回转电压点获取一阶回转曲线，测试电压加载步长1 V，一阶回转曲线对比结果如图11所示。并以每个回转曲线的仿真结果输出值与实验结果输出值的平均相对误差作为评判的参考，结果见表1。

由图11和表1可以看出，由本文建立的迟滞模型的仿真结果和实验所得的一阶回转曲线吻合度较高、误差较小，因此可得出本文所用的迟滞模型的建立方法为一种切实可行的方法。

4 结论

(1)详细阐述了压电作动器迟滞模型的建立理论，以实验的方式获得最小二乘支持向量机模型所需的一阶回转曲线。

(2)根据一阶回转曲线计算迟滞模型初始平均加权系数，并确定训练模型的输入输出，导入最小二乘支持向量机模型进行训练。将α-β平面划分为更多迟滞单元的组成形式，确定预测计算的输入值并将其导入训练后的模型得到最终的迟滞单元的平均加权系数，从而得到压电作动器的迟滞模型。

(3)通过仿真结果和实验结果的对比，得出本文基于最小二乘支持向量机所建立的模型能精确描述压电作动器的迟滞非线性特性，为一种有效的方法。本文方法加快了建模的速度，免去了需大量实验来获得一阶回转曲线从而计算加权系数的麻烦。

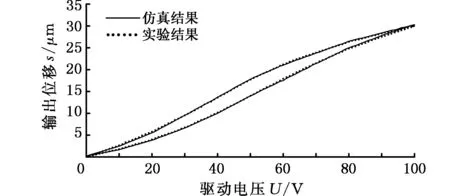
(a)电压U=100 V

(b)电压U=80 V

(c)电压U=60 V

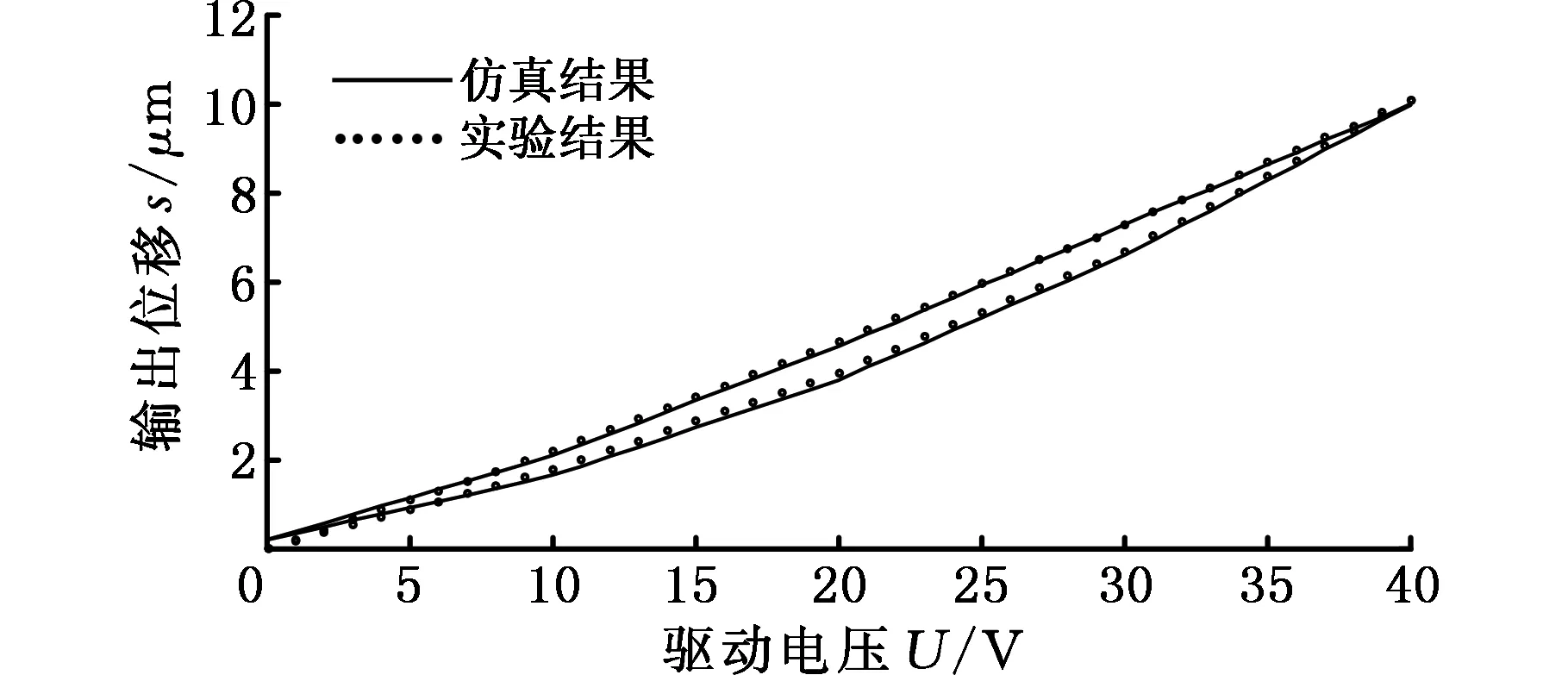
(d)电压U=40 V图11 仿真和实验结果对比图Fig.11 Contrast figure of simulation and experiment results

回转电压(V)最小相对误差(%)最大相对误差(%)1000.191.83800.231.52600.121.93401.562.01

参考文献：

[1] GUO Jiang, CHEE S K, YANO T, et al. Micro-vibration Stage Using Piezo Actuators [J]. Sensors and Actuators A: Physical,2013,194:119-127.

[2] CAI Kunhai, TIAN Yanling, WANG Fujun, et al. Development of a Piezo-driven 3-DOF Stage with T-shape Flexible Hinge Mechanism [J]. Robotics and Computer-integrated Manufacturing,2016,37:125-138.

[3] 王常松, 梁森, 韦利明. 智能微位移主动隔振控制系统的研究[J]. 振动与冲击,2015,34(13):211-216.

WANG Changsong, LIANG Sen, WEI Liming. A Smart Micro-displacementactive Vibration Isolation System [J]. Journal of Vibration and Shock,2015,34(13):211-216.

[4] BIGGIO M, BUTCHER M, GIUSTINIANI A, et al. Memory Characteristics of Hysteresis and Creep in Multi-layer Piezoelectric Actuators: an Experimental Analysis [J]. Physica B: Condensed Matter.,2014,435:40-43.

[5] 秦海辰, 尹周平. 压电陶瓷晶体迟滞特性的本构关系研究 [J]. 中国机械工程,2014,25(15):2059-2064.

QIN Haichen, YIN Zhouping. Research on Hysteresis Constitutive Relation in Piezoceramic Crystals [J]. China Mechanical Engineering,2014,25(15):2059-2064.

[6] FELIX W, SUTOR A, RUPITSCH S J, et al. A Generalized Preisach Approach for Piezoceramic Materials Incorporating Uniaxial Compressive stress[J]. Sensors and Actuators A: Physical,2012,186(10):223-229.

[7] LIU L, TAN K K, CHEN S, et al. SVD-based Preisach Hysteresis Identification and Composite Control of Piezo Actuators [J]. ISA Transactions,2015,51(3):430-438.

[8] CHOI G H, OH H J, CHIO S G. Repetitive Tracking Control of a Coarse-fine Actuator[C]// Proceedings of the 1999 IEEE/ASME International Conference on Advanced Intelligent Mechatronics. Atlanta,1999:335-340.

[9] XU Q S, LI Y M. Dahl Model-based Hysteresis Compensation and Precise Positioning Control of an XY Parallel Micromanipulator with Piezoelectric Actuation[J]. Journal of Dynamic Systems, Measurement, and Control,2010,132(4):1-12.

[10] WEI Z, WANG Daihua. Non-symmetrical Bouc-Wen Model for Piezoelectric Ceramic Actuators[J]. Sensors and Actuators A: Physical,2012,181(7):51-60.

[11] ZAMAN M A, SIKDER U. Bouc-Wen Hysteresis Model Identification Using Modified Firefly Algorithm [J]. Journal of Magnetism and Magnetic Materials,2015,395:229-233.

[12] 范家华, 马磊, 周攀, 等. 基于径向基神经网络的压电作动器建模与控制[J]. 控制理论与应用,2016,33(7):856-862.

FAN Jiahua, MA Lei, ZHOU Pan, et al. Modeling and Control of Piezoelectric Actuator Based on Radial Basis Function Neural Network[J]. Control Theory & Applications,2016,33(7):856-862.

[13] LI Pengzhi, YAN Feng, GE Chuan, et al. A Simple Fuzzy System for Modelling of Both Rate-independent and Rate-dependent Hysteresis in Piezoelectric Actuators [J]. Mechanical Systems and Signal Processing,2013,36(1):182-192.

[14] DONG Yangyang, HU Hong, WANG Hongjun. Identification and Experimental Assessment of Two-input Preisach Model for Coupling Hysteresis in Piezoelectric Stack Actuators [J]. Sensors and Actuators A: Physical,2014,220:92-100.

[15] TANG Hui, LI Yangmin. Feedforward Nonlinear PID Control of a Novel Micromanipulator Using Preisach Hysteresis Compensator [J]. Robotics and Computer-integrated Manufacturing,2015,34:124-132.

[16] DLALA E. Efficient Algorithms for the Inclusion of the Preisach Hysteresis Model in Nonlinear Finite-element Methods [J]. IEEE Transactions on Magnetics,2011,47(2):395-408.

[17] 赵新龙, 谭永红, 董建萍. 基于扩展输入空间法的压电执行器迟滞特性动态建模[J]. 机械工程学报,2010,46(20):169-174.

ZHAO Xinlong, TAN Yonghong, DONG Jianping. Dynamic Modeling of Rate-dependent Hysteresis in Piezoelectric Actuators Based on Expanded Input Space Method [J]. Journal of Mechanical Engineering,2010,46(20):169-174.

[18] MA Yingkun, ZHANG Xinong, XU Minglong, et al. Hybrid Model Based on Preisach and Support Vector Machine for Novel Dual-stack Piezoelectric Actuator [J]. Mechanical Systems and Signal Processing,2013,34(1/2):156-172.

[19] 张新锋, 赵彦. 基于最小二乘支持向量机的小样本威布尔可靠性分析[J]. 中国机械工程,2012,23(16):1967-1971.

ZHANG Xinfeng, ZHAO Yan. Weibull Reliability Analysis in Small Samples Based on LS-SVM[J]. China Mechanical Engineering,2012,23(16):1967-1971.

[20] CHEN T T, LEE S J. A Weighted LS-SVM Based Learning System for Time Series Forecasting [J]. Information Sciences,2015,299:99-116.

[21] KRASNOSEL’SKII M, POKROVSKII A. Systems with Hysteresis [M]. New York: Springer,1989.

[22] SMITH R. Smart Material Systems: Model Development [M]. Philadelphia: Society for Industrial and Applied Mathematics,2005.