车载设备对地铁车厢地板振动影响及评估方法
2018-04-24王永胜臧晓斌刘海涛赵清良曾亚平
王永胜 丁 杰,2 臧晓斌 刘海涛 赵清良 曾亚平
1.株洲中车时代电气股份有限公司技术中心,株洲,4120012.湘潭大学土木工程与力学学院,湘潭,411105
0 引言
现代动车、地铁大部分采用动力分散型车组,而为车辆运行提供动力、电力及通风等功能的主要设备一般都悬挂于车体底部(也有部分放置在车顶上),这些设备(如牵引变压器、换气装置及部分变流器等)内部存在明显的振源(如变压器、风机等有源设备[1]),产生的振动会通过车体传递到车厢内部引起地板等结构发生振动,当振动过大时会严重影响乘车舒适性。随着车体轻量化设计技术的应用,车身特别是地板的刚度降低,而变流器的功率在不断提升,车厢地板振动受变流器内部振源的影响越来越显著,与此同时,人们对乘车舒适性的要求越来越高,因此,主机厂及客户对动车、地铁车厢结构的振动情况也越来越关注[2-5]。目前,国内外已有学者针对有源设备与动车、地铁车体振动的关系开展了仿真和试验工作[6-9],但关于牵引变流器、辅助变流器等车载设备对车体特别是地板振动影响的研究还较少。
当前主机厂对车载设备振动的评估没有统一的标准或规范,一般是在设备装车后测试车厢内的振动水平是否满足GB/T 13441等标准的要求来进行评估,或以设备装车前在吊耳等关键测点处某一频率段(0~3 200 Hz)内的有效值作为评估指标。这些评估方法存在明显的不足之处:设备装车后评估若存在振动超标,则更换、改进的时间和经济成本较高;设备装车前的评估没有针对其振动特点和与车体的耦合作用开展,易造成评估结果不准确,即评估通过的设备装车后有时仍会出现振动过大的现象。由此,在供应商车间实现车载设备振动评估的研究显得尤为迫切。
本文以内部带变压器等振源的地铁车辆辅助变流器为研究对象,分析其对地铁车厢地板振动的影响,并针对现有车间振动评估方法不足的情况提出了一种通过车间台架测试进行评估的方法。
1 振动测试及分析
某地铁车辆辅助变流器出厂之前,在车间进行了振动评估,0~3 200 Hz频率段内的加速度有效值为0.25 m/s2,表明振动满足主机厂要求(评价指标为该值不大于0.3 m/s2)。然而,在该辅助变流器装车通电测试中发现车厢地板振感明显,严重影响乘车舒适性,因此,需开展一系列的排查与分析工作。
1.1 振动测试
通过现场初步排查,基本确定振动是由辅助变流器引起的。为进一步了解地铁车厢地板振动的特性及分析相关原因,分别进行了辅助变流器装车通电测试及车间台架通电测试。装车通电测试时(图1),在辅助变流器吊耳及车厢地板同时布置15个三向振动传感器;车间台架测试时(图2),为模拟装车实际情况,将变流器安装在测试台架上,在变流器与台架连接固定的吊耳处布置传感器,与装车测试保持一致,且测试工况均保持一致。

图1 装车测试Fig.1 Loading test

图2 车间台架测试Fig.2 Workshop bench test
1.2 结果分析
经验表明,辅助变流器内部振源为变压器和冷却风机,其中变压器是主要的振动来源。本节分别对辅助变流器装车通电测试及车间台架通电测试数据进行分析。
1.2.1装车测试分析
辅助变流器装车通电运行时,车厢地板振感明显,测量得到加速度有效值为0.587 m/s2。选择一节没有安装辅助变流器的车厢进行测试,地板振动加速度有效值仅为0.05 m/s2。由此说明,辅助变流器的运行会对车厢地板振动产生影响。图3所示为有/无辅助变流器的车厢地板振动频谱对比,可以看出,安装辅助变流器车厢地板的振动主要集中在100 Hz,另外在24 Hz、150 Hz、200 Hz、300 Hz等处也有体现,其中100 Hz、150 Hz、200 Hz、300 Hz振动是由变压器磁致伸缩效应[10]引起的电磁振动,24 Hz振动由转速为1440 r/min的冷却风机引起。未安装辅助变流器的车厢地板振动频谱较为平缓。安装辅助变流器的车厢地板100 Hz振动值远大于其他频率(高出25 dB以上),且处于人体振动敏感区间,可以初步确定来自变压器100 Hz的电磁振动是引起车厢地板振动过大的主要原因。
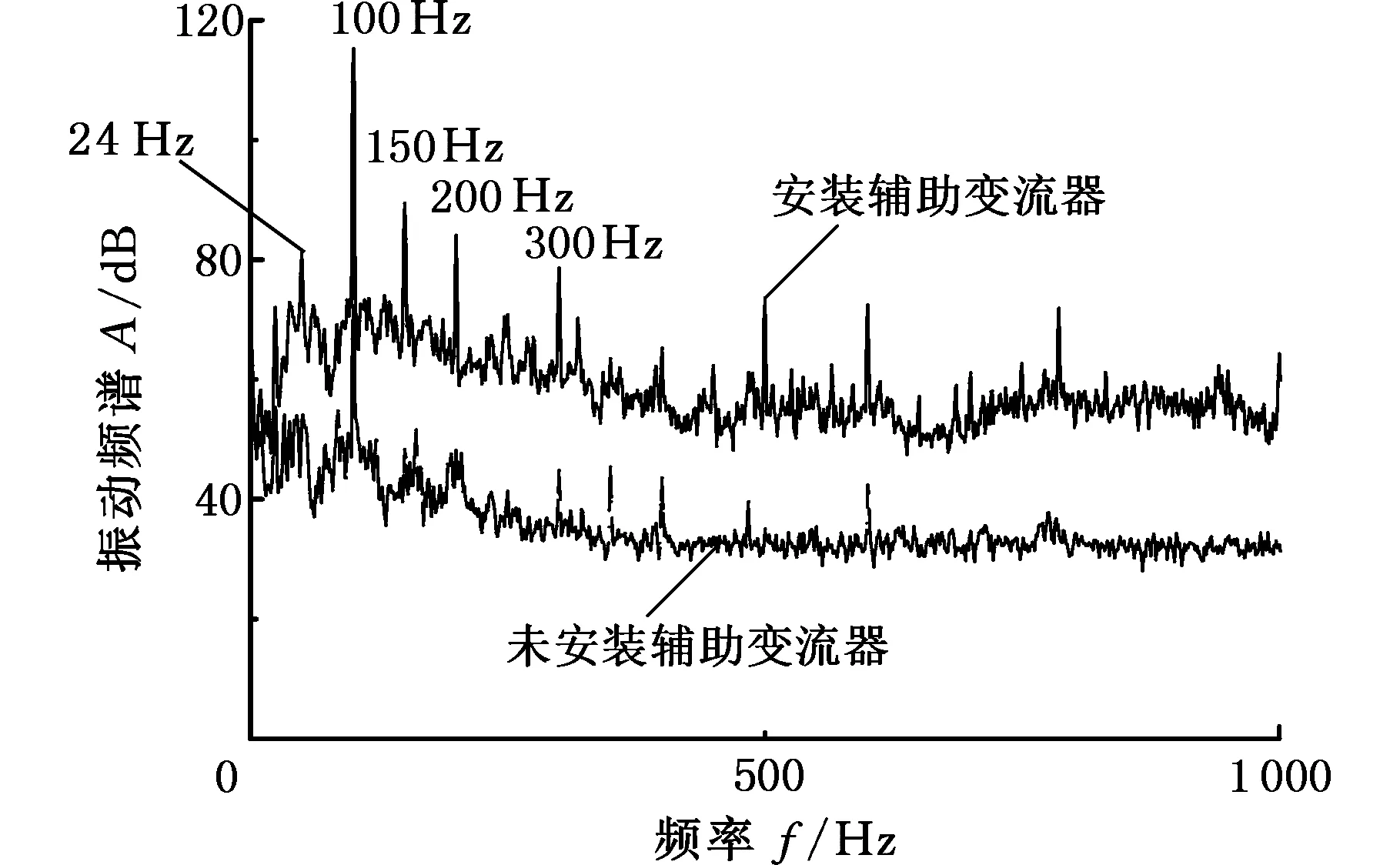
图3 车厢地板振动频谱对比Fig.3 Comparison of vibration spectrum of car floor
1.2.2车间台架测试分析
对变流器等车载设备振动的现有评估方法是,测试接口位置的振动数据,对某一频率段(如0~3 200 Hz)的加速度有效值进行平均处理,得到振动评估值。通过该方法测试获得该型辅助变流器吊耳处的加速度有效值平均水平为0.252 m/s2,是满足现有装车要求的。同时选择第二款变压器(为便于区别,原装车的变压器记为变压器A,第二款变压器记为变压器B)安装在该辅助变流器柜中,进行同样的测试与评价,可知辅助变流器吊耳处的加速度有效值平均水平为0.27 m/s2,亦满足现有装车要求,且变压器A的加速度有效值小于变压器B的加速度有效值。
前面已经确定变压器100 Hz电磁振动是引起车厢地板振动过大的主要原因,故将分别装有变压器A、B的辅助变流器12个吊耳处垂向100 Hz的振动加速度有效值进行比较,如图4所示。由图4可看出,安装变压器A时12个吊耳垂向100 Hz振动加速度有效值均明显大于变压器B的加速度有效值。由此,可以推测安装变压器B后车厢地板的振动将降低,而现有的对变流器等车载设备振动评估方法和指标并不能有效预测其对地板振动的影响。
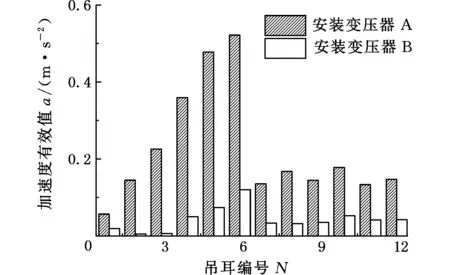
图4 车间台架测试12个吊耳处垂向100Hz振动对比Fig.4 Comparison of vertical 100Hz vibration between 12 lifting lugs in workshop bench test
1.3 共振分析
前面分析已经基本确定变压器的100Hz电磁振动是引起车厢地板振动过大的主要原因,但为了慎重起见,需进一步排除电磁振动从辅助变流器传递到车厢地板中发生共振的风险。本文利用锤击法测试分析辅助变流器及车辆其他设备不通电时,静态工况下从变流器安装吊耳到车厢地板的传递函数,将其中一个通道的力-加速度传递函数列出,如图5所示。由图5可知,辅助变流器静态工况下,振动从车体安装吊耳传递到车厢地板过程中,在100 Hz处不存在明显的放大现象,其他通道结论类似,因此基本可排除辅助变流器与车体耦合发生共振而放大100 Hz振动的风险,可以确定车厢地板振动过大是由于辅助变流器内部变压器振源振动能量过大引起的。同时本文还利用激振器对车厢地板进行了扫频试验,试验结果也显示,在100 Hz等主要振动频率附近车厢地板没有明显的共振现象。针对此类问题的解决,
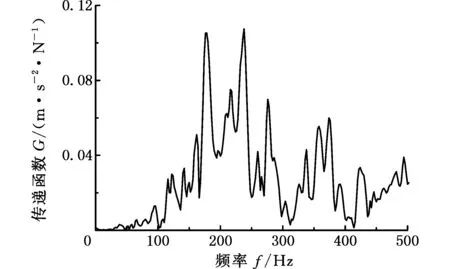
图5 车体安装吊耳到地板间的力-加速度传递函数关系Fig.5 The force -acceleration transfer function between the car body and the lifting lugs
一般是从振源、传递路径和受体三个方面考虑。由于现场更改车体、辅助变流器结构等难度较大,因此本文主要从振源——辅助变流器内部变压器着手。
2 辅助变流器振动评估方法的理论基础
目前,无论是主机厂还是设备供应商,变流器等有源设备振动对动车、地铁车体内部地板等结构的影响主要是通过装车测试来评估的,这种评估方法虽然直观有效,但存在以下缺点:①以某一频率段振动有效值进行评估,忽略了关键频率点,易造成误判;②无法提前预估,使得对变压器一类的振源设备选型比较盲目、被动,一旦装车后车体振动过大,则改进难度大且所需成本较高,易导致批量产品出现振动问题。由此,现急需一种能在制造商车间或实验室对车载有源设备振动进行有效评估的方法。
2.1 理论模型
本文提出的评估方法涉及变流器在车间或实验室台架振动测试和装车振动测试两个时间和空间上都不连续的系统,具体如图6所示。图6中,X1(t)为振源(如变压器、风机、电机等)输出的振动信号,Y1(t)n是振动传感器在变流器与测试台架安装接口位置处测得的振动信号,其中,n为测试信号通道数(n=1,2,…,m;m为通道总数);Y2(t)n是振动传感器在变流器与车体安装接口位置处测得的振动信号;Y3(t)为车内地板评价点的振动信号(一般选择体感振动最强烈的位置)。为便于对比,两个系统安装接口状态、测点的位置和方向以及运行工况等均保持一致。
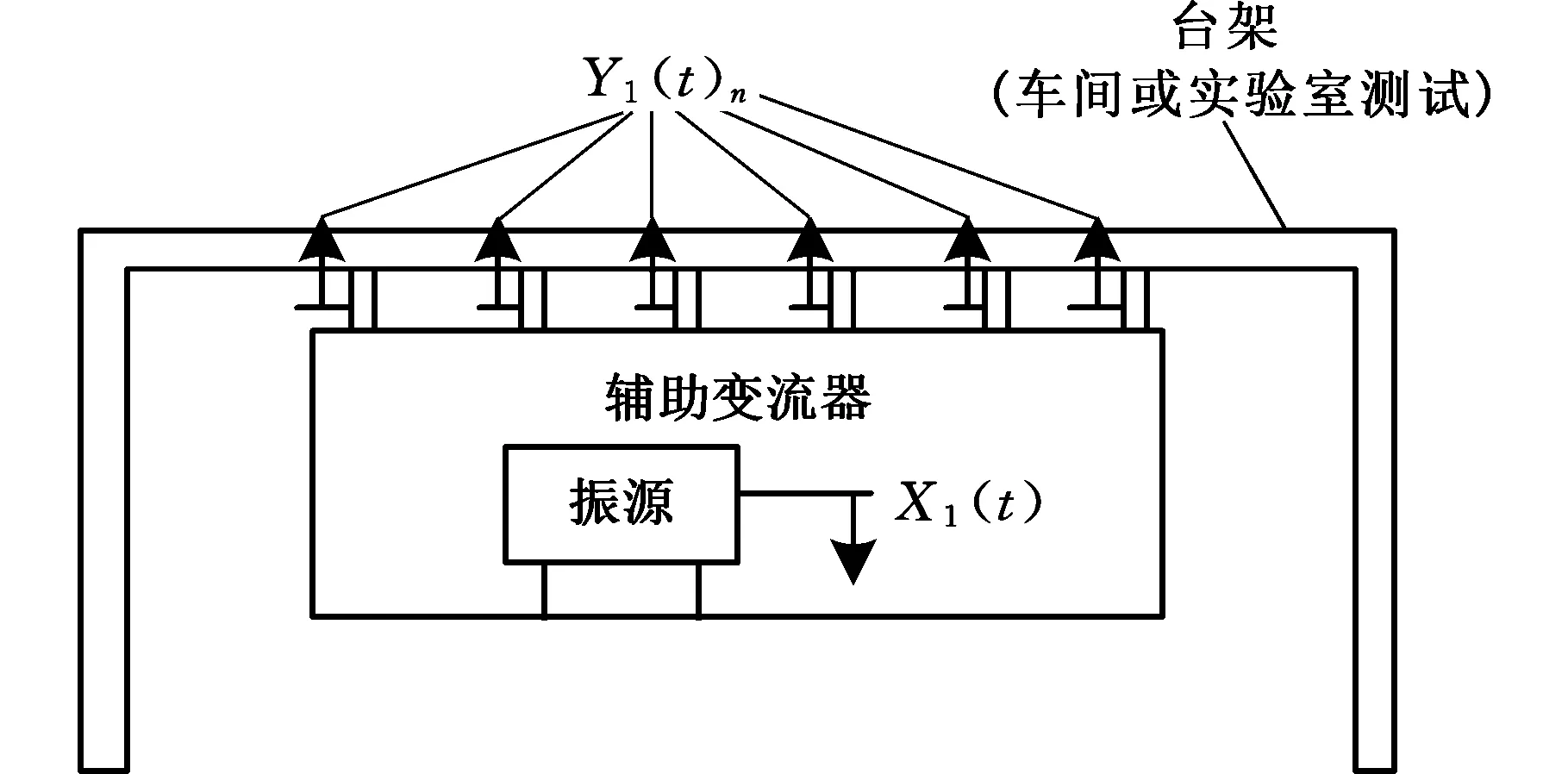
(a)车间或实验室台架振动测试系统
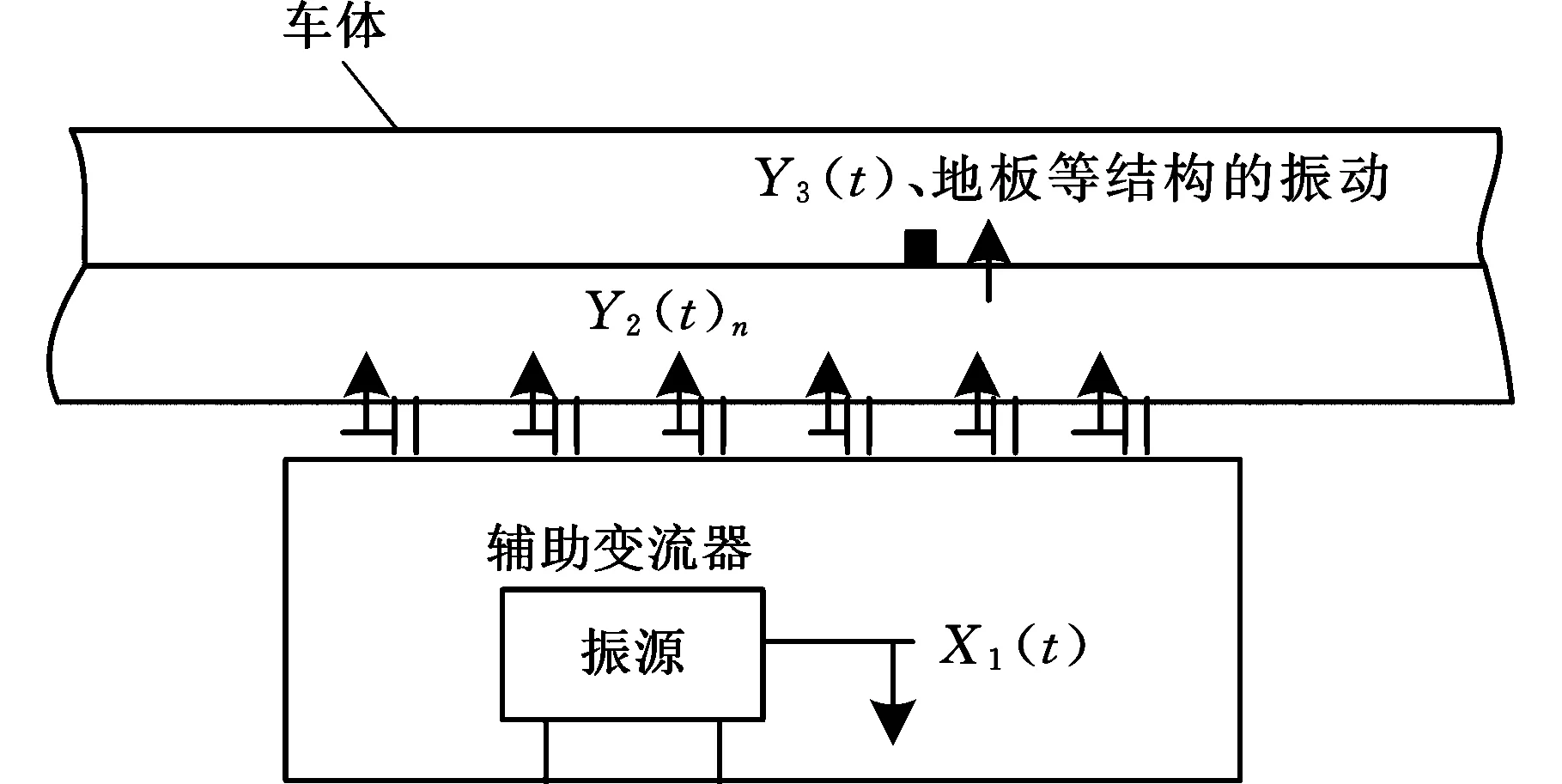
(b)装车振动测试系统图6 振动测试系统模型Fig.6 The model of vibration testing system
假设图6中两个测试系统为线性定常系统,忽视非线性和时变等因素影响,则两个测试系统振动传递过程可用图7表示。其中,G1(s)n、G2(s)n、G3(s)n分别为3个子系统的振动传递函数。

(a)台架振动测试系统振动传递
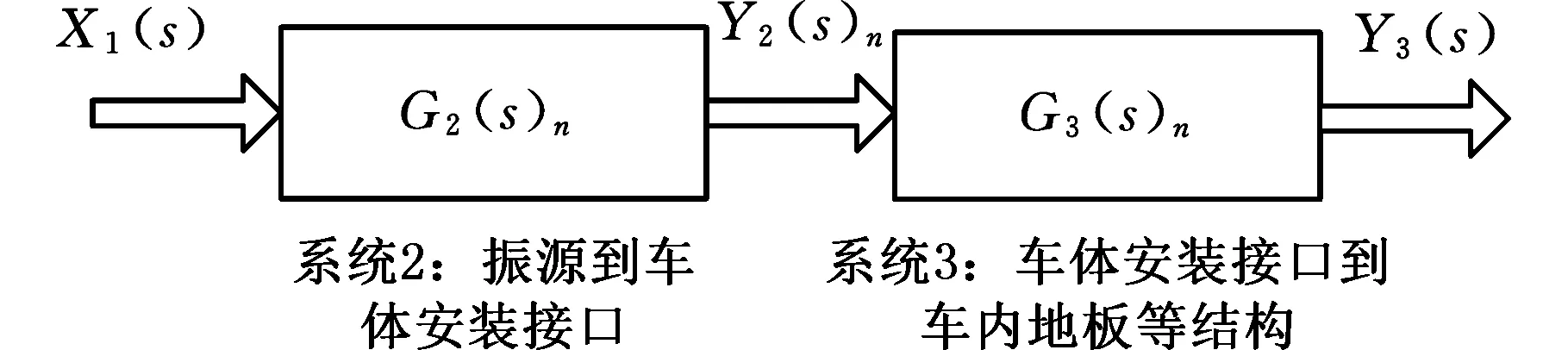
(b)装车振动测试系统振动传递图7 振动传递系统模型Fig.7 The model of vibration transfer system
图7中两个测试系统可分为3个子系统,其中X1(s)、Y1(s)n、Y2(s)n和Y3(s)分别由信号X1(t)、Y1(t)n、Y2(t)n和Y3(t)经拉普拉斯变换后得到:
(1)
式中,L为拉普拉斯变换符号;s为复变量,s=ε+jω。
对于3个线性定常子系统,可以得到[11]:
(2)
2.2 不连续系统的近似连续化
由于车间台架振动测试系统及装车振动测试系统在时间和空间上都不连续,因此,参考文献[12]的思想:引入一个虚拟系统来将两个系统近似连续化,得到图8所示的从车间台架测试到装车测试的连续系统。
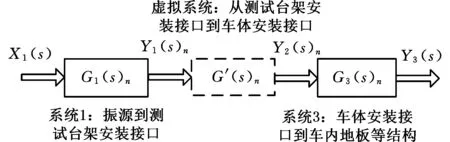
图8 近似连续系统的振动传递模型Fig.8 Vibration transfer model of approximate continuous system
对于图8中近似连续系统振动传递模型,根据式(2)可作以下推导:
(3)
令
(4)
即G′(s)n为车间台架安装接口信号到车体安装接口信号这个虚拟系统的传递函数。这样从变流器车间或实验室台架测试到装车测试就构成了一套连续系统(图8)。通过测试或仿真得到近似连续系统的传递函数,就可以利用车间或试验室测试数据完成变流器振动对动车、地铁车体内部地板等结构影响的近似评估。
2.3 车厢地板振动计算
通过车间测试的数据以及近似连续系统的传递函数即可得到各通道传递到车厢地板评价点的振动输出信号:
(5)
通过拉普拉斯逆变换,即可求得Y3(s)n的时域信号:
(6)
式中,Y3(t)n为计算得到的变流器振动通过通道n传递到车厢地板的振动信号。
3 辅助变流器振动评估过程及试验验证
3.1 辅助变流器振动评估过程
根据前面的理论,利用车间振动测试数据及测试或仿真得到的系统传递函数,即可完成辅助变流器振动的评估。首先,利用车间台架试验获得变流器台架安装接口处的振动信号Y1(t)n,并通过拉普拉斯变换得到Y1(s)n;其次,通过引入虚拟系统将图7中测试系统1、3串起来,利用样品测试数据或以往类似安装形式产品测试数据等获得虚拟系统的传递函数G′(s)n;然后,通过车体实测数据或类似车型测试数据等获得系统3的传递函数G3(s)n;最后,利用式(5)和式(6)得到各通道传递到车厢地板评价点的振动信号Y3(t)n。具体过程如图9所示。
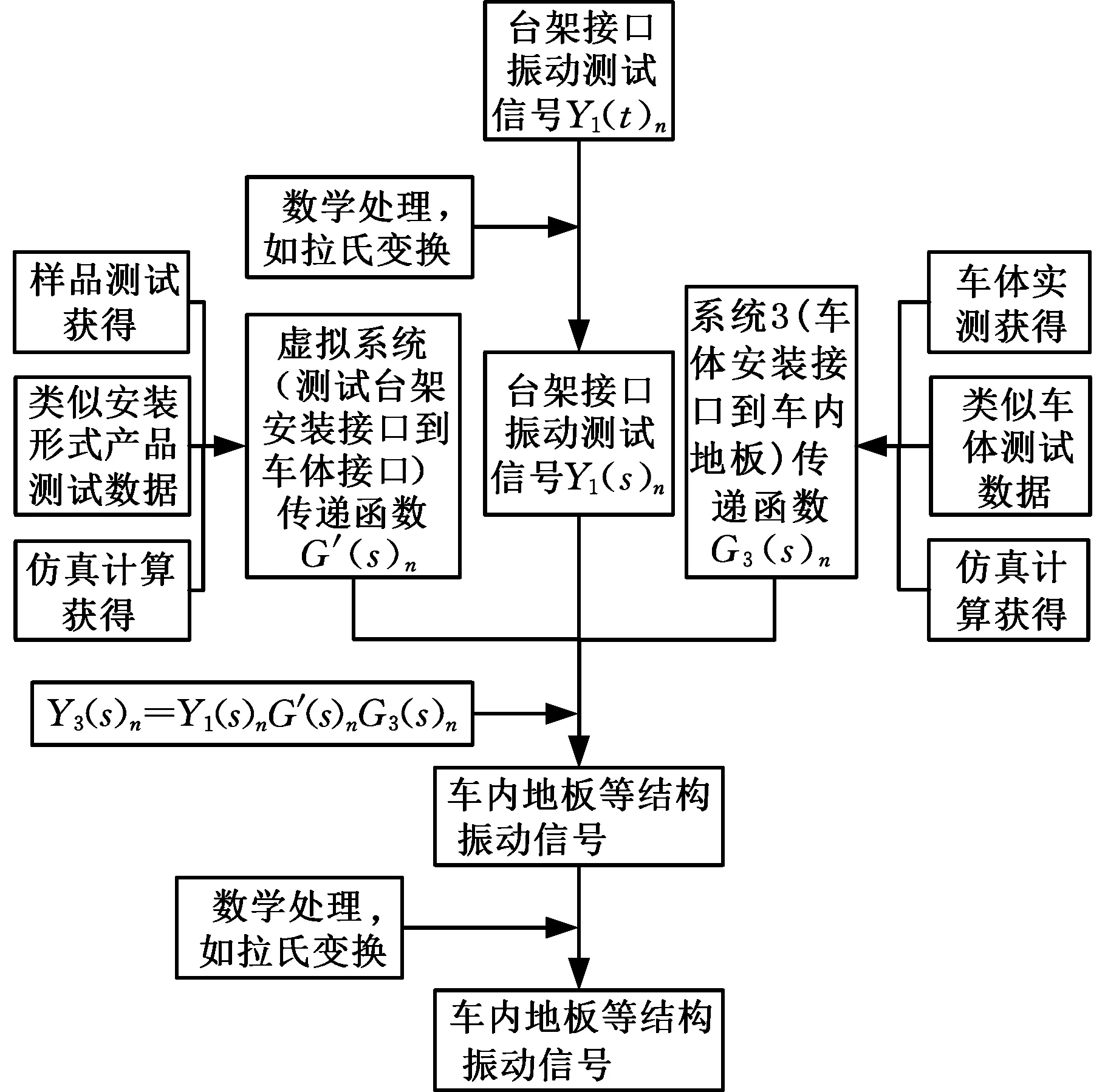
图9 辅助变流器振动评估过程Fig.9 Vibration evaluation process of auxiliary converter
3.2 评估结果统计分析
传递函数反映系统本身的动态特性,只与系统动态参数有关,与外界输入无关,因此,根据前面评估方法计算得到的各通道传递到车厢地板评价点的振动信号Y3(t)n理论上是相同的,即
Y3(t)=Y3(t)1=Y3(t)2=…=Y3(t)n
(7)
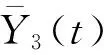
3.3 试验验证
为验证本文提出的辅助变流器振动评估方法,利用安装变压器A实测的传递函数数据对安装不同型号变压器(B、C、D)时车厢地板的振动有效值进行评估计算。考虑到车载设备振动对车体的影响往往体现在一些关键频率点(如变压器振动频率为电源频率的2倍),而影响较小的频率振动传递过程中易受到非线性等因素的影响,信噪比较差,因此,本文利用不同型号变压器验证所述评估方法时主要考虑电源的2倍频(即100 Hz振动)。按所述方法计算得到更换变压器B、C、D后车厢地板100 Hz振动加速度有效值,并与实际装车的数据对比,如表1所示。由表1可知,更换变压器B、C、D后,车厢地板100 Hz振动加速度有效值的计算值与实测值误差在10%左右,说明该方法准确性较高。
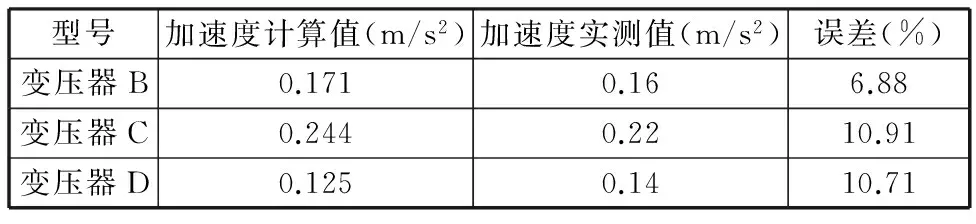
表1 更换变压器后的地板100 Hz振动有效值对比Tab.1 Comparison of the effective values of 100 Hzfloor vibration after changing transformer
综合其他因素考虑,最后选择将该条线路地铁辅助变流器内的变压器A全部更换为变压器B,从而很好地解决了该地铁车辆地板批量振动过大问题。图10为安装变压器B与原变压器A的地板实测振动加速度频谱对比。由图10可知,通过本文方法评估变压器振动并进行更换后,车厢地板的振动有效值明显减小,地板上的振动加速度值已满足人体振感要求,说明该方法对于评估辅助变流器等车载设备的振动具有工程应用价值,能够减少设备厂商和主机厂由于设备更换带来的损失,改善用户体验。
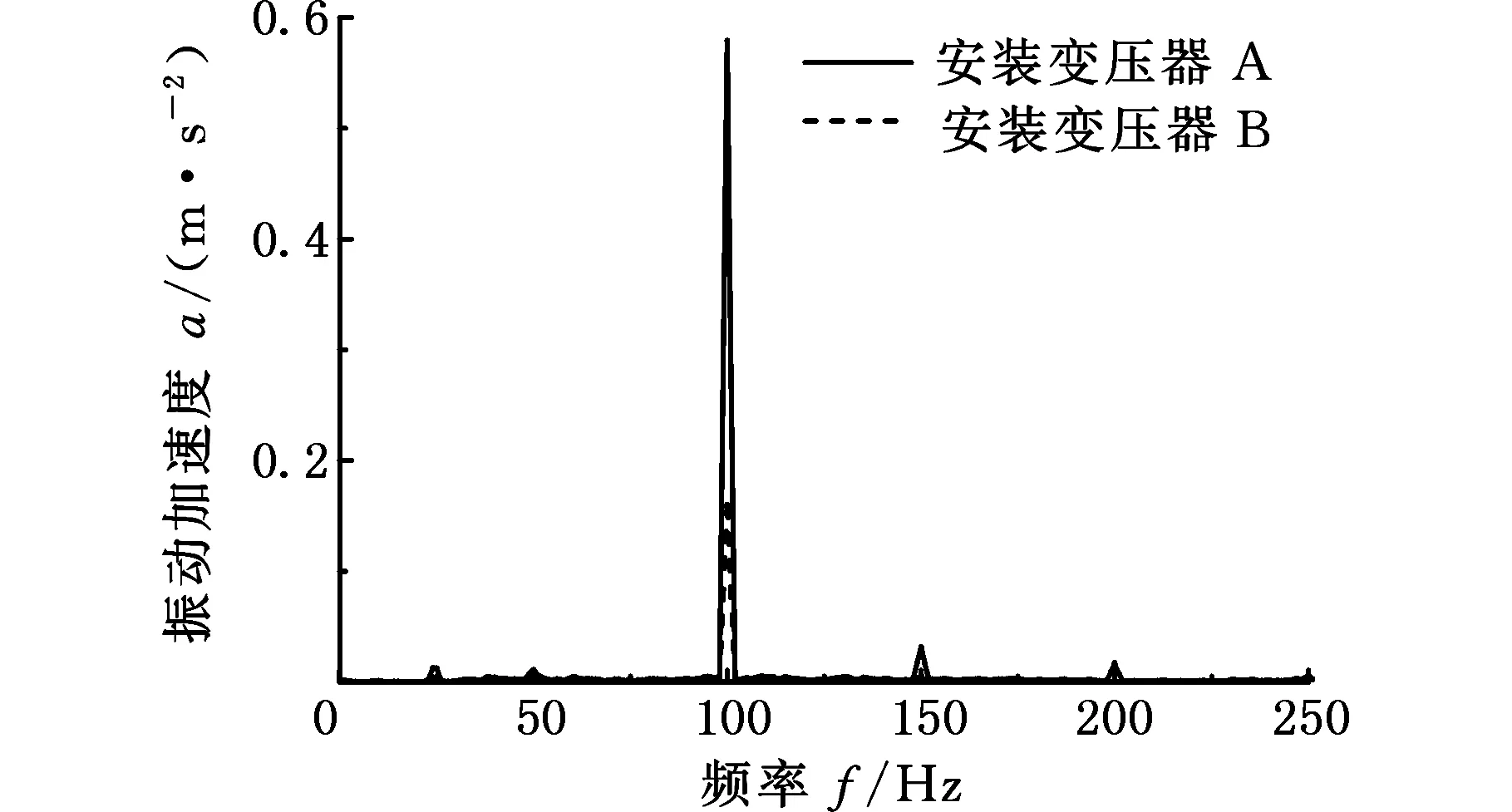
图10 安装变压器A与B时车厢地板振动频谱对比Fig.10 Comparison of vibration spectrum of car floor when installing the transformer A and B
4 结论
(1)本文提出的评估方法通过引入虚拟系统概念将两个时间、空间不连续的系统近似连续化,能够在车间或实验室提前对变流器等车载设备进行振动评估。
(2)通过试验验证,本文提出的评估方法计算值与试验值误差在10%左右,其准确性满足工程应用要求,且该方法还可应用于风机、电机、牵引变压器等有源车载设备的振动评估。
(3)车载设备振动评估除考虑设备本身的振动特性外,还应考虑设备与车体的耦合作用,因此后续将联合设备生产商和主机厂商开展进一步研究。
参考文献:
[1] 余建勇.有源设备与车体耦合参数优化研究[D].成都:西南交通大学, 2013.
YU Jianyong. Coupling Parmeters Optimization Research of Excitation Source Device and Carbody[D].Chengdu: Southwest Jiaotong University,2013.
[2] WENNBERG D. Light-weighting Methodology in Rail Vehicle Design through Introduction of Load Carrying Sandwich Panels [D]. Stockholm:KTH Royal Institute of Technology,2011.
[3] SHI Huailong, LUO Ren, WU Pingbo, et al. Influence of Equipment Excitation on Flexible Carbody Vibration of EMU[J]. Journal of Modern Transportation,2014,22(4):195-205.
[4] 张济民,胡用生,陆正刚.轨道车辆运行过程中人体振动仿真研究[J].振动与冲击,2007,26(10):76-80.
ZHANG Jimin, HU Yongsheng, LU Zhenggang. Vibration Simulation of Human Body on Running Railaway Vehicle[J]. Journal of Vibration and Shock,2007,26(10):76-80.
[5] 国云鹏,宋桂秋.基于高速铁路随机振动环境对人体腰椎影响的人机工程座椅设计[J].中国机械工程,2015,26(3):389-393.
GUO Yunpeng, SONG Guiqiu. Ergonomic Seat Design Based on High-speed Rail Random Vibration Environment Effects on Human Lumbar[J]. China Mechanical Engineering,2015,26(3):389-393.
[6] 邱飞力,张立民,张卫华. 悬挂参数对出口车辆动力学性能的影响[J]. 噪声与振动控制,2014,34(2):98-102.
QIU Feili, ZHANG Limin, ZHANG Weihua. Analysis of the Effect of Suspension Parameters on the Dynamic Performance of an Export Train[J]. Noise and Vibration Control,2014,34(2):98-102.
[7] 吴会超,邬平波,吴娜,等. 车下设备悬挂参数与车体结构之间匹配关系研究[J]. 振动与冲击,2013,32(3):124-128.
WU Huichao, WU Pingbo, WU Na, et al. Matching Relations between Equipment Suspension Parameters and a Carbody Structure[J]. Journal of vibration and shock,2013,32(3):124-128.
[8] 张远亮,张立民. 某动车牵引变压器振动及传递分析[J]. 铁道机车车辆,2015,35(1):32-35.
ZHANG Yuanliang, ZHANG Limin. Analysis of Vibration and Vibration Transmission for EMU Traction Transformer[J]. Railway Locomotive & Car,2015,35(1):32-35.
[9] 罗光兵,曾京,罗仁. 车下设备悬吊方式对车体振动的影响[J].铁道学报,2015,37(5):9-14.
LUO Guangbing, ZENG Jing, LUO Ren. The Influence of Underframe Equipment Suspended Types on Carbody Vibrations[J]. Journal of the China Railway Society,2015,37(5):9-14.
[10] 付强.电力机车主变压器故障诊断技术研究[D]. 长沙:中南大学,2013.
FU Qiang. The Research on Fault Diagnosis Technology of Electric Locomotive Main Transformer[D]. Changsha:Central South University,2013.
[11] 金海薇,郑海起,高永生,等. 复杂机械系统的传递函数表示方法[J]. 科学技术与工程,2015,7(13):3219-3221.
JIN Haiwei, ZHENG Haiqi, GAO Yongsheng,et al. Transfer Function Express Method of Complex Mechanical System[J]. Science Technology and Engineering,2015,7(13):3219-3221.
[12] 李香军. 几类不连续动态系统理论及应用[D]. 哈尔滨:哈尔滨工业大学,2009.
LI Xiangjun. Theory and Applications of Several Discontinuous Dynamical Systems[D]. Harbin: Harbin Institute of Technology,2009.
