基于支持向量机的电火花加工8418钢表面粗糙度预测模型
2018-04-24余剑武胡其丰
余剑武 胡其丰 文 丞 柳 波 沈 湘
湖南大学机械与运载工程学院,长沙,410082
0 引言
8418钢作为AISI H13钢的改进型,具有优良的抗热疲劳龟裂、热冲击开裂、热磨损、塑性变形的性能,这些独特的性能使其成为压铸、热锻、热挤模具钢的最佳选择[1]。电火花加工(EDM)技术由于其在加工复杂形状工件上的优势,已成为制造复杂形状挤压模具的关键工艺,其加工后的工件表面质量对挤压模具性能及使用寿命有重要影响[2]。工件表面粗糙度Ra是影响电火花加工表面质量的关键因素之一,它主要受放电参数、工作介质、电极材料的影响[3-5]。
近年来,许多学者对电火花加工后的表面粗糙度进行了研究。何淑菊等[6]针对电火花加工表面粗糙度的正态分布特性及测量误差进行了分析。但是因电火花加工工艺过程非常复杂,涉及许多电参数和非电参数,而这些参数与加工后的表面粗糙度之间关系又具有不确定性,故直接采用精确的数学模型来表达是很难的。在实际工程中,一般都依靠加工经验来设置加工参数。
人们对放电参数进行了大量的研究。杨晓冬等[7]采用神经网络的方法,针对电火花加工工艺的特点及复杂性,提出了一个型腔电火花加工工艺效果的预测模型,可映射出电参数和加工结果之间的关系,并分析了引起预测误差的原因。GAO等[8]将人工神经网络和遗传算法相结合,建立了电火花加工参数优化模型,采用遗传算法进行参数优化。JIANG[9]采用最小二乘支持向量机(LS-SVM)方法来估计车铣磨的表面粗糙度。
上述研究都忽略了加工过程的非电因素,同时还有一些研究者是以大量实验数据作为参考基础来建立模型的。
通过大量文献的比较,支持向量机的方法已被广泛应用于车铣磨的表面粗糙度[10]估计。于明鑫等[11]提出了一种基于灰度信息和支持向量机的人眼检测方法,使用训练的支持向量机分类器精确检测人眼区域位置,且获得较好的检测效果。在前期研究阶段,余剑武等[12]提出了一种基于支持向量回归理论的数学方法,建立了适用于电火花加工工艺指标结果预测的模型,同时,利用遗传算法对该方法中的各参数进行优化,预测不同电火花加工参数组合下的工艺指标,模型预测结果与实验结果两者相关系数能达到90%以上,说明模型可以用于描述加工工艺指标的结果预测。
为了进一步研究电火花加工后的表面质量,本文基于支持向量机的方法建立一个适用于电火花加工表面粗糙度预测的模型(简称“电加工表面粗糙度模型”),同时应用遗传算法对该模型中的参数进行优化。
1 电加工表面粗糙度模型
电火花加工的物理原理比较复杂,加工后表面质量的影响因素较多,包括电参数和非电参数,这些加工参数之间存在着非线性关系,直接用较为精确的数学模型很难表达。针对电火花加工的这种非线性特性,建立电加工表面粗糙度预测模型。
1.1 表面粗糙度
表面粗糙度是指加工表面具有的较小间距和微小峰谷的不平度,其外形轮廓示意图见图1。表面粗糙度
(1)
其中,l为采样长度;f(x)为X线上部和下部的面积,在X线上的面积为正,线下为负,并且X线上部分面积和下部分面积相等。
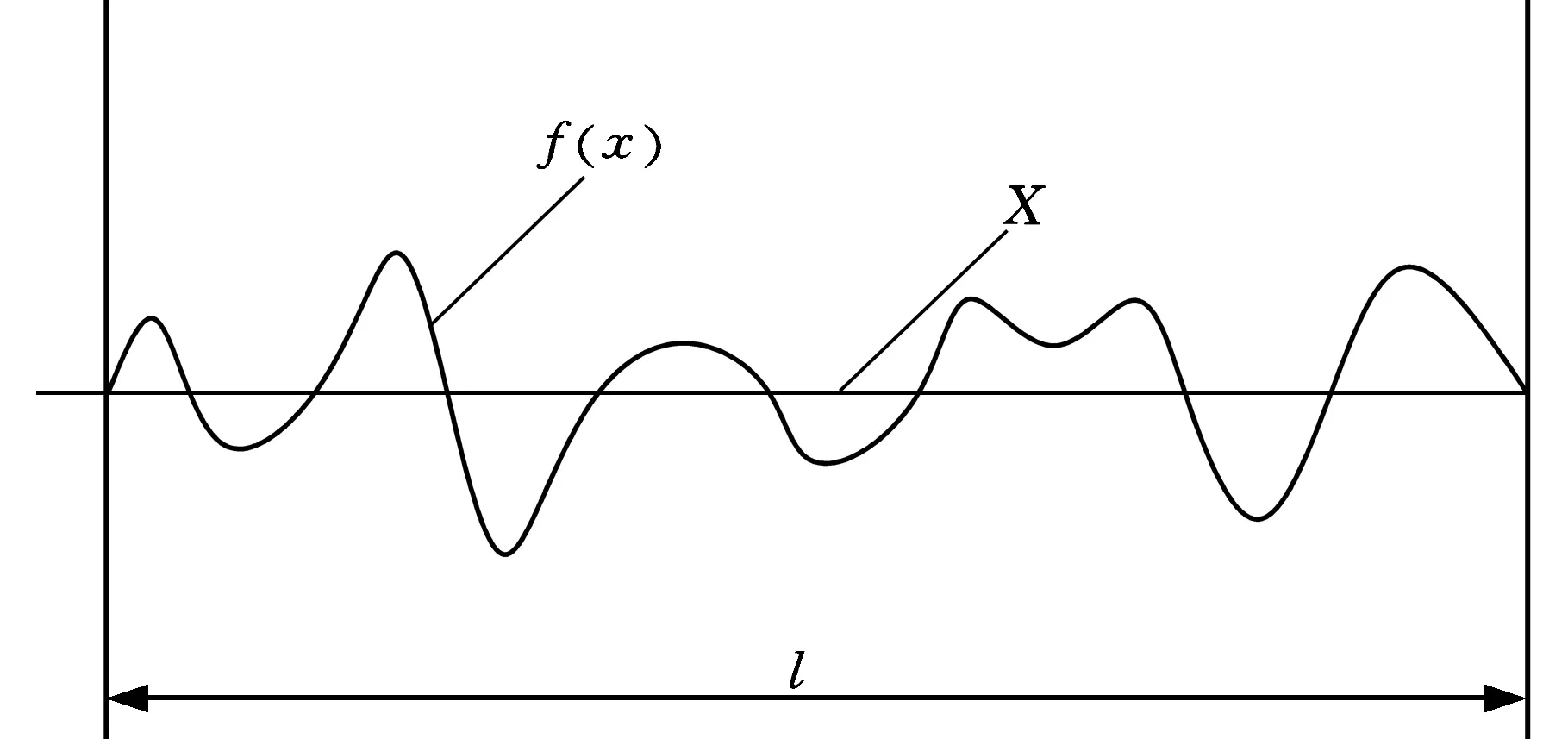
图1 电加工后工件表面轮廓示意图Fig.1 Schematic diagram of workpiece surface after EDM
1.2 表面粗糙度Ra数学模型
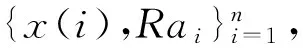
y(x)=yRa(x)=wTφ(x)+b
(2)
其中,wT是向量,φ(x)是向量x经过非线性映射得到的高维特征空间向量,y(x)表示一超平面;偏差b可以通过下式求得:
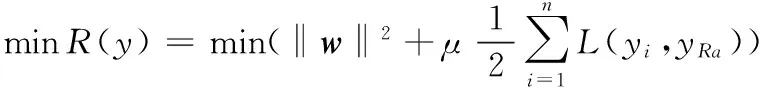
其中,L(yi,yRa)是损失函数;μ是惩罚系数,用来控制训练误差和模型复杂性之间的平衡,其值越大,模型误差越小。
为了保证支持向量机的粗糙度预测模型精度,引入一个小正数ε,即管径,使得
|yi-y(x)|=|Rai-yRa(x)|≤ε
(4)
对于一超平面,其最优就是需要分割间隙最大,同时为保证最优化问题有解,引入松弛变量ξ、ξ*,因而最优化问题可以用下面的数学模型来描述:
(5)
s.t.wTφ(x)+b-yi≤ε+ξi
(6)
(7)
(8)
i=1,2,...,n
式(5)~式(7)构成二次规划问题,通常解法是引入拉格朗日算子,故相应的拉格朗日函数为
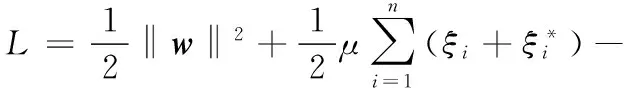
(9)
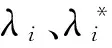
(10)
(11)
(12)
根据Mercer条件有
k(xi,xj)=φT(xi)·φ(xj)
(13)
其中,k(xi,xj)为核函数,因电火花加工中具有明显的非线性,所以需要选一个非线性的核函数,本文表面粗糙度预测模型中,选择高斯核函数,即径向基函数。高斯核函数相比其他核函数预测精度更高,结果更稳定,其表达式如下:
(14)
式中,σ为核函数宽度。
综上,可得电火花加工表面粗糙度预测模型:
(15)
2 实验
本实验中电火花成形机床的装备结构如图2所示。实验采用CuW70电极(45 mm×φ8 mm) 通过电火花成形机床加工8418钢(20 mm×20 mm×10 mm),以美孚特效火花机油为工作液,加工方式为负极性加工,孔深为2 mm。影响加工后表面粗糙度值的放电因素主要有:峰值电流、间隙电压、开路电压、脉宽、占空比等参数,非电参数因素有跳升(电极抬起的高度)、冲液方式、放电时间等。针对峰值电流、间隙电压、开路电压、脉宽、占空比、跳升这6项参数,以8418钢加工后的表面粗糙度为目标,设计了六因素五水平正交试验,实验条件及实验结果如表1所示。在正交试验25组数据中,随机先后选出5组数据作为模型的测试数据,其余20组作为模型的训练样本数据。本实验采用JB-4C表面粗糙度仪检测表面粗糙度。
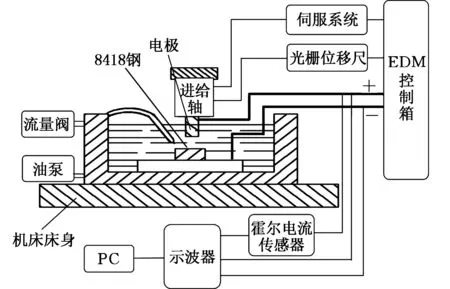
图2 电火花成形机床的装备结构图Fig.2 Equipment structure drawing of EDM
3 遗传算法优化模型参数
3.1 适应度函数的设计
采用遗传算法对电加工表面粗糙度预测模型中参数进行优化时,适应度函数的选择是非常重要的。在回归问题中,一般采用平均平方误差和平方相关系数这两个参数指标。本研究中采取平均平方误差作为模型的适应度函数,其表达式如下:
(16)

表1 电火花加工8418钢实验条件与结果Tab.1 Experimental conditions and results of 8418 steel by EDM
3.2 电加工表面粗糙度预测模型算法流程
为了提高模型的泛化能力,还需要选择惩罚系数μ、损失系数ε和核函数参数σ并优化这些参数。采用遗传算法优化这些参数,其初始值随机选择,最大代数设为200,采用预测值与实验值之间的平均平方误差作为适应度值,从而选取最优的模型参数。最终选取表面粗糙度预测模型中的μ、ε、σ值分别为498、0.02、57.8。
电加工表面粗糙度预测模型算法流程如图3所示。在遗传算法进化过程中,对开路电压、间隙电压、峰值电流、脉宽、占空比、跳升6个参数进行编码,将每个个体分成6个子串,前5个子串由十位二进制组成,分别表示开路电压、间隙电压、峰值电流、脉宽、占空比,最后1个子串由五位二进制组成,表示跳升。染色体选择操作采用轮盘赌法,交叉操作采用两个个体之间的算术交叉,变异操作采用边界变异的方法。
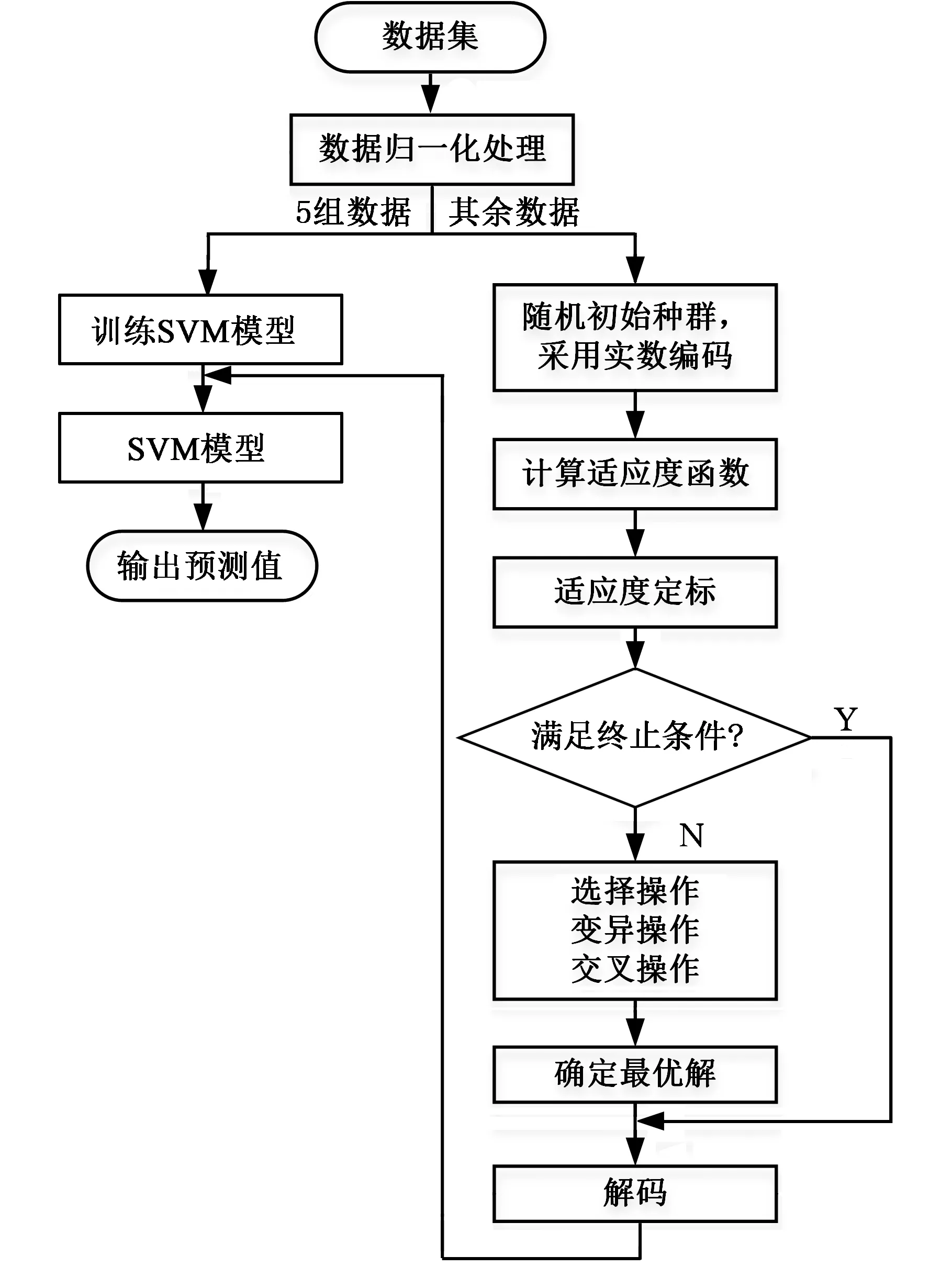
图3 表面粗糙度预测模型算法流程图Fig.3 Flow chart of surface roughness prediction model
4 实验结果与模型参数优化分析
从实验中先后选出5组数据作为模型的测试数据,对所建立的电加工表面粗糙度预测模型进行测试,测试结果如表2所示。粗糙度预测值和实验值的误差分析如图4所示。
本文的研究对象是有多种配方,生产炼钢用铁水、铸铁用铁水等多种铁水产品的炼铁厂,本文对所研究的问题作出以下假设:
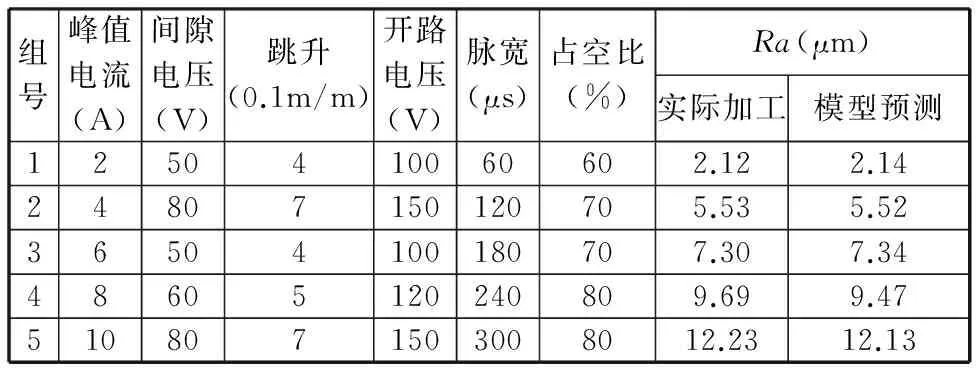
表2 剩余5组参数对模型的测试结果Tab.2 The remaining 5 sets of parameters of the model group test results
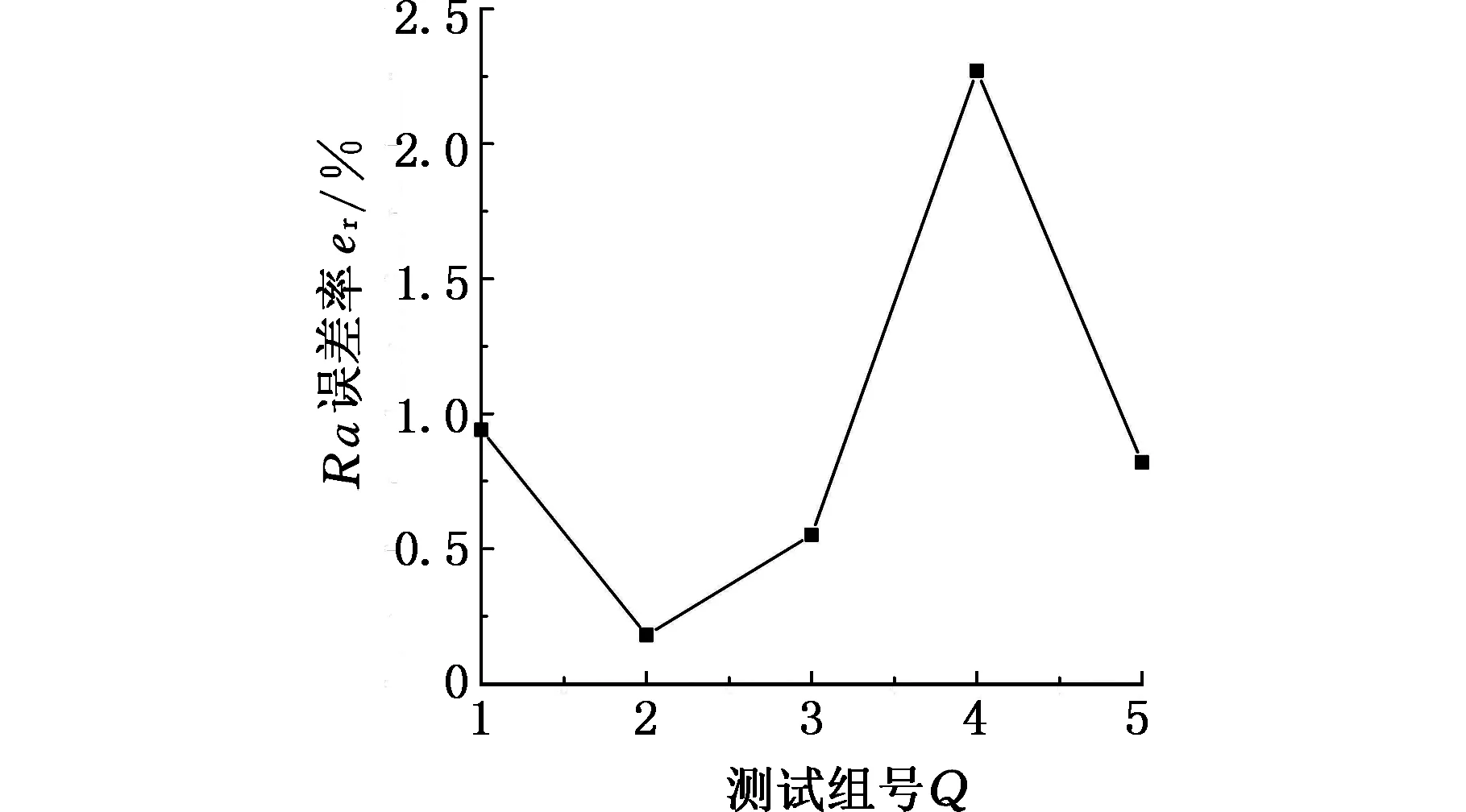
图4 模型预测结果与实际加工的误差分析Fig.4 Error analysis of model prediction and experiment
由表2可知,电加工表面粗糙度预测模型的测试误差较小,该模型基本可以描述不同参数组合下电加工表面粗糙度值;图4中,第4组参数的预测值和实验值误差最大,为2.27%。影响电火花加工表面质量的因素较多,不同的粗糙度下,预测值的精确度也有所波动,但是误差率都在5%内,说明电加工表面粗糙度预测模型精度较高。
5 结论
(1)针对电火花加工的非线性特性,采用了支持向量机的方法建立了电加工表面粗糙度预测模型,对电火花加工后工件质量的研究具有一定的参考价值。
(2)采用预测值与实验值之间的平均平方误差作为其适应度值,利用遗传算法优化所建立模型中的参数,提高了电加工表面粗糙度预测模型预测数据的精确度。
(3)利用MATLAB结合加载的LIBSVM工具箱,对电火花加工表面粗糙度进行预测,然后用预测值与实验值进行对比分析,每组的误差都在5%以内,说明所建立的电加工表面粗糙度预测模型精度较高,可以用于预测加工后工件表面粗糙度。
参考文献:
[1] 张忠侃. H13钢碳化物球化过程及组织力学性能的研究[D]. 昆明:昆明理工大学,2010.
ZHANG Zhongkan. Study on Spheroidizing Process and Mechanical Properties of Carbides in H13 Steel [D]. Kunming: Kunming University of Science and Technology,2010.
[2] ALTANA T, LILLYB B, YEN Y C, et al. Manufacturing of Dies and Molds[J]. CIRP Annals—Manufacturing Technology,2001,50(2):404-422.
JIANG Dongmei. Experimental Study on the Influence of Machining Parameters on Surface Roughness in EDM [J]. Manufacturing Machinery,2010,48(12):79-81.
[4] 文武,王西彬,龙震海,等. 多曲率油槽电火花成形加工及精密组合电极的设计[J]. 中国机械工程,2009,20(8):946-949.
WEN Wu, WANG Xibin, LONG Zhenhai, et al. EDM of Oil Supply Tank with Multi-curvature and Design of Accurate Assembly Electrode [J]. China Mechanical Engineering,2009,20(8):946-949.
[5] 王化团, 任小中. 35P型电火花机床电参数对工件表面粗糙度的影响分析[J]. 安阳工学院学报,2013,12(2):7-9.
WANG Huatuan, REN Xiaozhong. Analysis of Influence of Electrical Parameters on Based on 35P EDM Machine [J]. Journal of Anyang Institute of Technology,2013,12(2):7-9.
[6] 何淑菊, 邱英. 电火花加工表面粗糙度的正态分布特性及测量误差分析[J]. 实验技术与管理,2005,22(11):32-35.
HE Shuju, QIU Ying. Normal Distribution Characteristics and Measurement Error Analysis of EDM Surface Roughness [J]. Experimental Technology and Management,2005,22(11):32-35.
[7] 杨晓冬, 赵万生, 刘光壮,等. 基于神经网络的型腔电火花加工工艺效果预测模型[J]. 航空制造技术,2001(3):41-43.
YANG Xiaodong, ZHAO Wansheng, LIU Guangzhuang, et al. Forecasting Model of Technological Effect for Die Sinking EDM Based on ANN [J]. Aeronautical Manufacturing Technology,2001(3):41-43.
[8] GAO Qing, ZHANG Qinhe, SU Shupeng, et al. Parameter Optimization Model in Electrical Discharge Machining Process [J]. Journal of Zhejiang University Science A,2008,9(1):104-108.
[9] JIANG Zhuoda. Intelligent Prediction of Surface Roughness of Milling Aluminium Alloy Based on Least Square Support Vector Machine [C]// Control and Decision Conference (CCDC). Xuzhou: IEEE,2010:2872-2876.
[10] WANG Peigong, MENG Qingfeng, ZHAO Jian,et al. Prediction of Machine Tool Condition Using Support Vector Machine [J]. Journal of Physics: Conference Series,2011,305(1):12113-12121.
[11] 于明鑫, 周远松, 王向周,等. 基于灰度信息和支持向量机的人眼检测方法[J]. 工程科学学报,2015(6):804-811.
YU Mingxin, ZHOU Yuansong, WANG Xiangzhou, et al. Eye Detection Method Using Gray Intensity Information and Support Vector Machines [J]. Chinese Journal of Engineering,2015(6):804-811.
[12] 余剑武, 何利华, 段文,等. 电火花加工8418钢的工艺预测模型[J]. 机械工程学报, 2016, 52(11):207-212.
YU Jianwu, HE Lihua, DUAN Wen, et al. Study on Technology Forecasting Model of 8418 Steel in EDM [J]. Journal of Mechanical Engineering, 2016, 52(11):207-212.
