汽车侧风稳定性动态耦合方法研究

罗泽轩 谷正气,2 黄泰明 丰成杰 李舒雅

1.湖南大学汽车车身先进设计制造国家重点实验室，长沙，4100822.湖南文理学院，常德，415000

0 引言

行驶中的汽车受到周围环境风的影响,其运动状态会发生改变，产生侧滑或横摆运动，影响汽车行驶稳定性，造成行车安全问题。随着汽车车速的不断提高，关系到行车安全的汽车侧风稳定性问题日益引起人们的重视。

目前针对汽车侧风稳定性的研究主要通过数值仿真计算与风洞实验等方法来实现。其中风洞实验主要是进行稳态侧风下的汽车稳定性研究[1]，如人们提出的横摆模型[2]、牵引模型[3]等方法，但以上方法只能研究汽车模型在某一固定状态下受到的稳态气动力，无法考虑汽车在侧风作用下其运动状态的改变，即无法研究汽车在侧风作用下的侧滑或横摆运动，更不能研究该运动给汽车周围流场带来的反馈作用。因此,对于汽车侧风稳定性问题的研究,风洞实验有较大的局限性。数值仿真计算方法较风洞实验更为灵活，对于该问题的研究，既能考虑汽车在侧风作用下产生的侧滑或横摆等运动状态，更能分析该运动状态给汽车周围流场带来的反馈影响，实现空气动力学与系统动力学之间的双向耦合[4]。然而，受流体仿真软件中动网格技术及计算资源的限制，对汽车侧风稳定性的耦合研究多为静态的，即静态耦合模拟。静态耦合与实际中汽车以某一车速直线行驶时受到来自于车身侧向的环境风干扰这一情况主要有两点区别:一是两者流场性质不同[5]；二是静态耦合无法真实地模拟出车速及侧风风速，实际中汽车的运动状态与流场是一个动态耦合的过程。通过静态耦合模拟出的结果势必影响汽车侧风稳定性的分析。为了更准确地分析出汽车的侧风稳定性，在耦合方法的基础上，实现高速汽车侧风下的动态耦合模拟分析，真实地模拟汽车受侧风环境的干扰是十分必要的。

针对上述问题，基于已有的研究，本文提出了一种动态耦合方法，该方法将车速与侧风进行解耦处理，实现了侧风条件下汽车的动态模拟分析以及汽车空气动力学与系统动力学的动态耦合。

1 动力学模型

1.1 空气动力学模型

建立某实车空气动力学模型,如图1所示，由于本文流体仿真部分涉及车身表面网格的运动，为了防止出现网格畸变从而导致仿真计算失败，在不影响计算精度以及原车型整体气动特性的前提下，对原始模型进行了适当的简化处理[6]，忽略车门把手、雨刮器及后视镜支架等细小部件，并对车底盘做平整化处理。

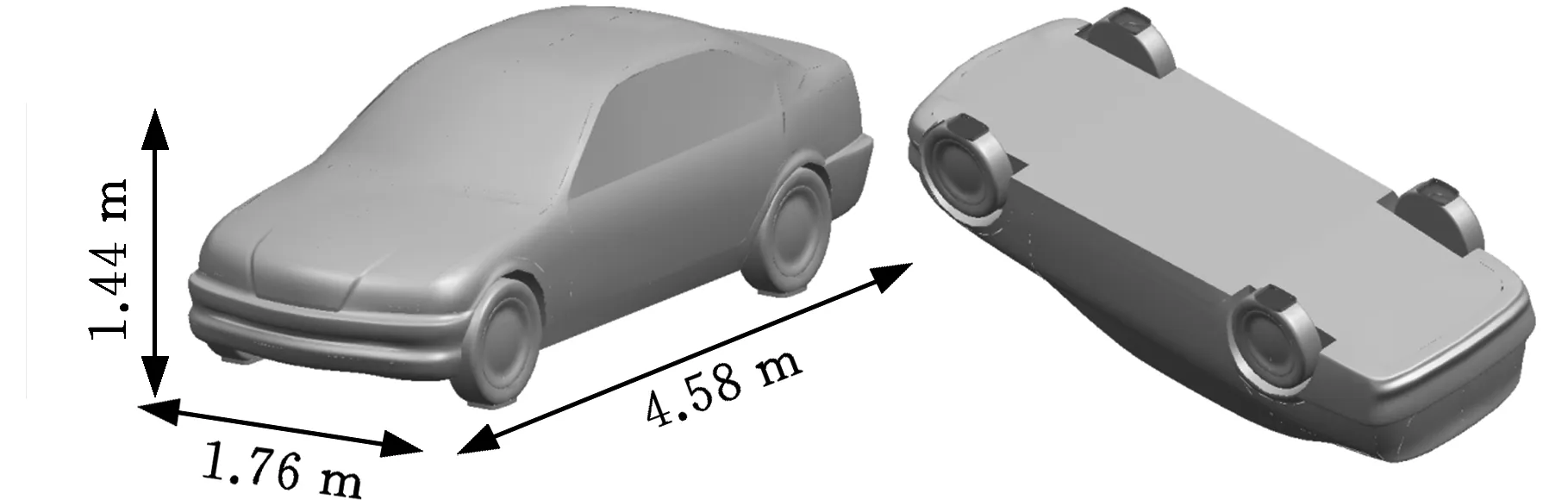
图1 简化汽车模型Fig.1 Simplified vehicle model

根据汽车的外形及侧风环境的特点，将流体计算域设置为长方体形状，计算域相关边界条件如表1所示。

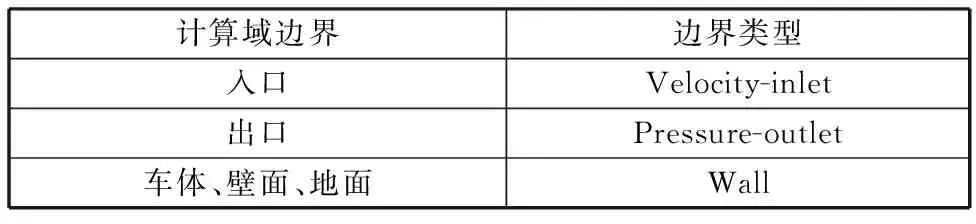
表1 边界条件设置Tab.1 The settings of boundary condition

同时选取Realizablek-ε湍流模型进行流场稳态计算，待流场稳定后改用函数LES进行流场瞬态求解。该湍流模型能够有效地应用于包括剪切流、边界层流动等不同类型的流动模拟[7]，其控制方程如下:

(1)

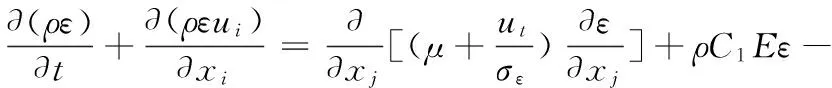
(2)

式中,ρ为流体密度；xi、xj为坐标轴分量；μ为流体的黏性系数；t为时间；ut为t时刻的速度；ui为速度分量；k为湍动能系数；ε为涡黏性系数；σk、σε分别为关于k与ε的湍流普朗特施密特数；Gk为关于k的经验公式；E、C1、C2、η均为常数，由实验确定。

1.2 系统动力学模型

为了便于分析汽车侧风稳定性的基本特征，对一简化为线性二自由度的汽车模型进行研究，不考虑转向系统及悬架的作用，车厢只作平行于地面的平面运动，且汽车车速u视为不变，即认为汽车只有横摆和侧向运动这两个自由度[8]，轮胎采用魔术轮胎模型[9]。其中，二自由度动力学模型主要参数如表2所示，车辆坐标系的原点与汽车质心Cm重合，整车动力学模型受力分析[8]如图2所示，FYi为轮胎所受侧偏力，u1、u2与α1、α2分别为前后轴中点的速度及前后轮侧偏角。

表2 动力学模型相关参数

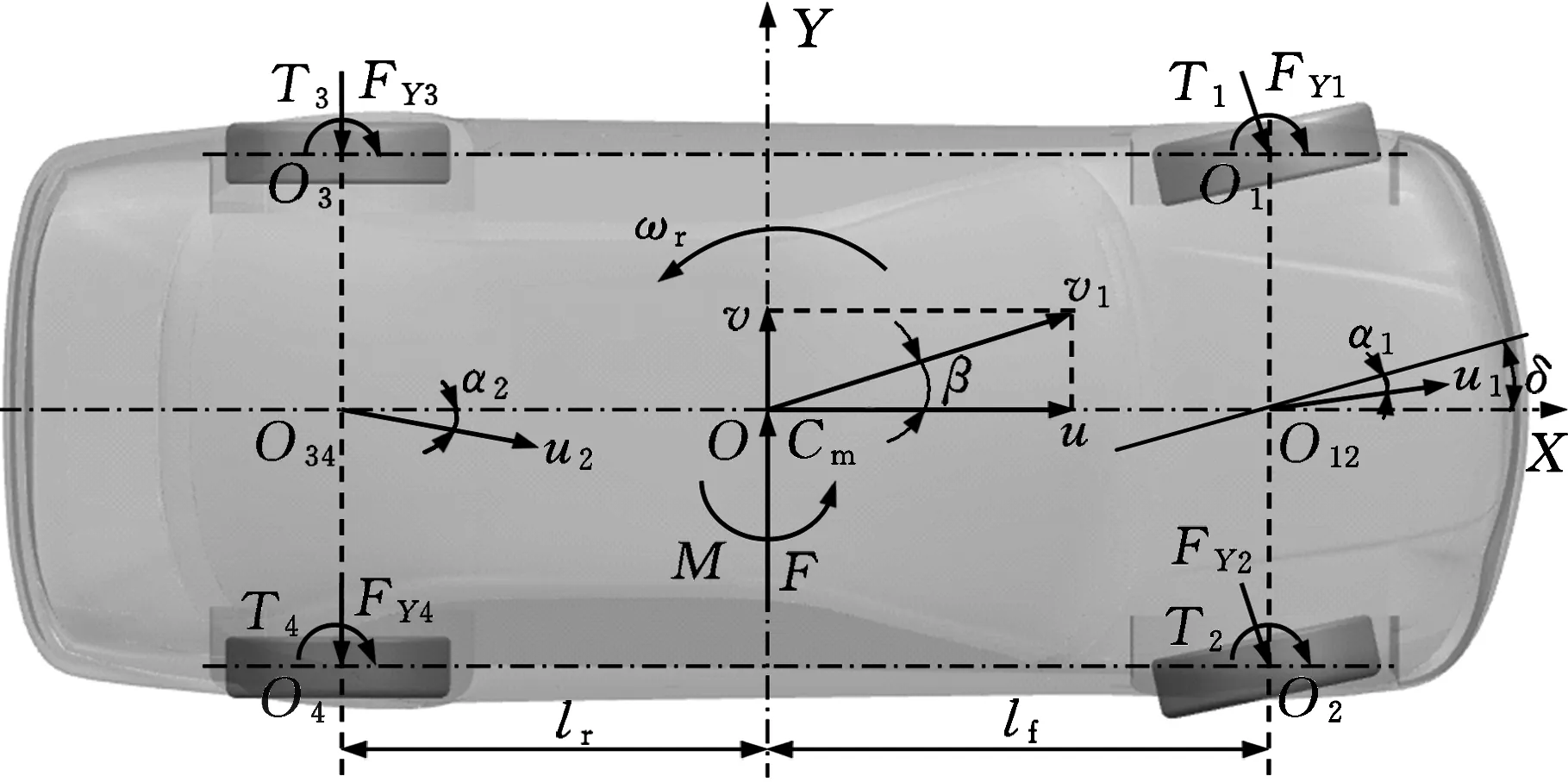
图2 整车动力学分析Fig.2 Vehicle dynamics analysis

考虑侧风条件下的汽车二自由度整车模型的微分方程如下：

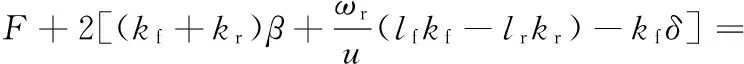
(3)

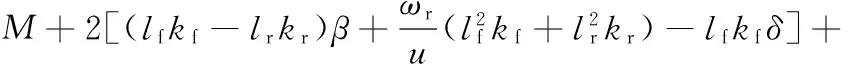
(4)

式中,F、M分别为汽车所受气动侧向力和横摆力矩；β为质心偏角；ωr为汽车横摆角速度；δ为前轮转角，由于不考虑转向，其值为零；v为汽车侧向速度；Ti为回转力矩,由魔术公式[9]求得。

2 动态耦合方法

2.1 耦合方法

耦合仿真方法分为流体计算与系统动力学计算两部分，分别通过FLUENT与MATLAB实现。仿真过程中FLUENT与MATLAB均存在两个状态，即计算状态与扫描状态，计算状态进行正常的仿真计算，而扫描状态则是通过监控程序对共享文件夹进行循环扫描，监控等待另一软件上一步仿真的结果。FLUENT通过函数UDF来读取共享文件夹中的侧向速度v和横摆角速度ωr，并将该步仿真得到的侧向力F和横摆力矩M写入共享文件夹[10]，而MATLAB则通过m文件从共享文件夹读取侧向力F和横摆力矩M，并且将计算得到的v和ωr写入共享文件夹从而实现两者的数据交换[11]，仿真流程如图3所示。

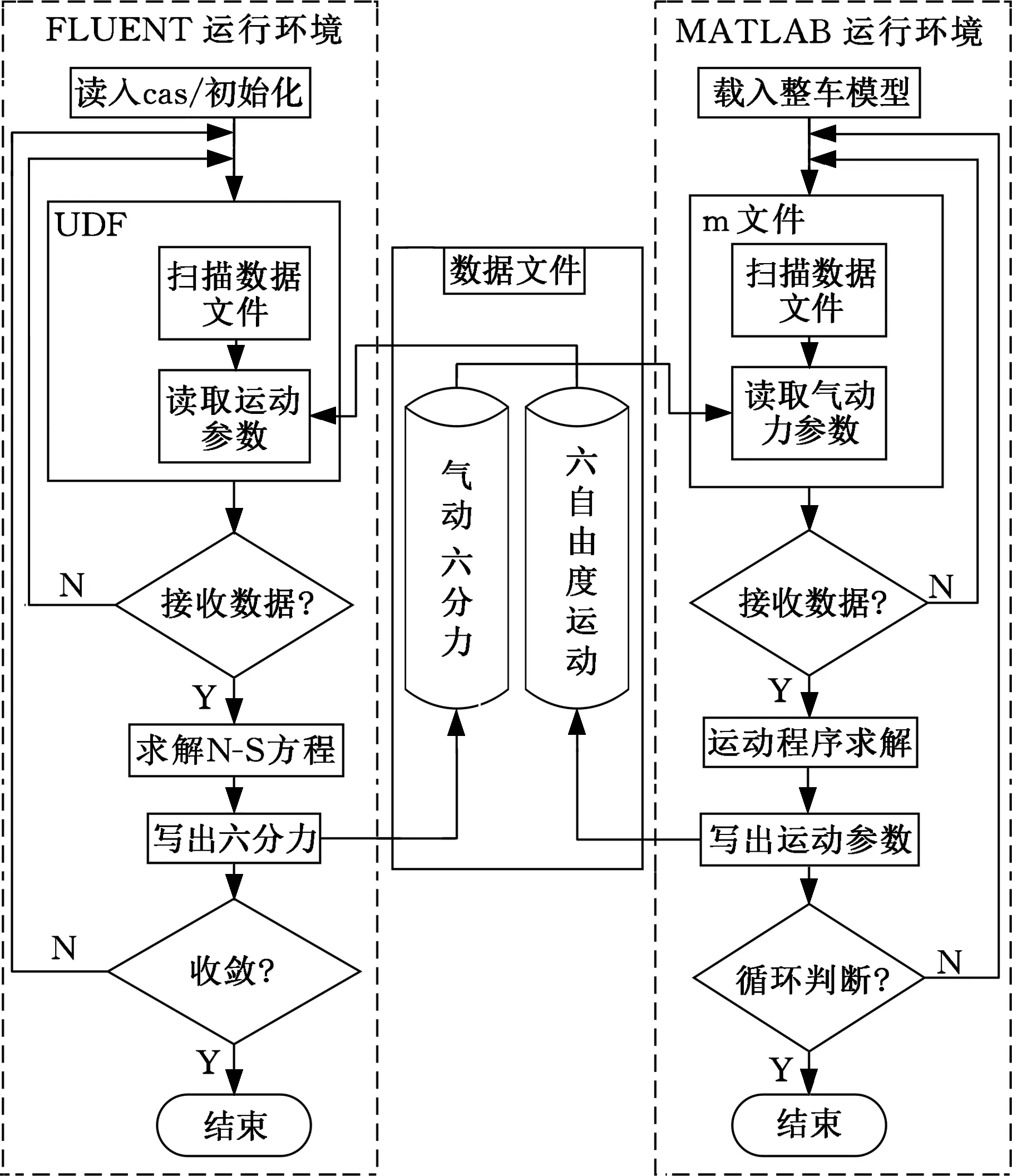
图3 双向耦合仿真流程Fig.3 Two-way coupling realization process

两者在循环仿真的过程中分别读取对方上一步计算所得的结果作为该时间步仿真的激励，以此来实现车身运动状态与流场的耦合作用，即空气动力学与系统动力学的耦合，其迭代仿真步骤如图4所示。

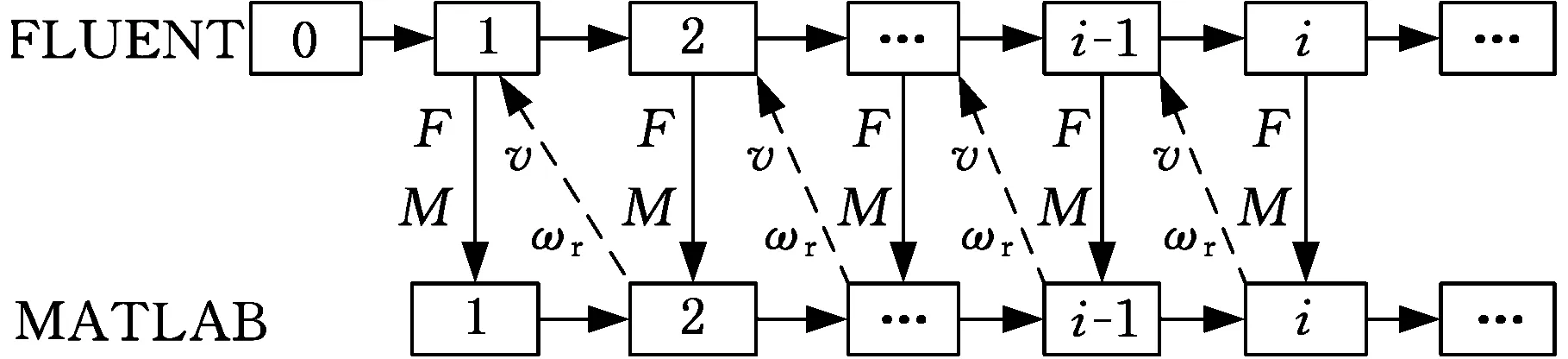
图4 双向耦合迭代步骤Fig.4 Iterate method of two-way coupling

2.2 静态耦合方法

静态耦合方法中的静态指的是仿真分析中对车速的模拟方式为静态，而非指模型在流场中处于静止状态,即惯性系下利用相对速度原理模拟车速，以图5入口1中-X方向的静态风速u模拟汽车的车速，仿真过程中汽车在X方向无速度，而Y方向在侧风作用下是有侧向速度的。侧风则以入口2中-Y方向的风速vy模拟，而计算时实际加载的风速为模拟车速u与侧风速度vy的合速度v1，θ为该加载风速方向与u的夹角。静态模拟中流体计算域设置为入口1距车头4倍车长(4L)，出口1距车尾20倍车长(20L)，左侧入口距车左侧3倍车宽(3W)，右侧出口距车右侧12倍车宽(12W)，总高度5倍车高(5H)，阻塞比1.43%，满足要求。该计算域与侧风模拟方式如图5所示。

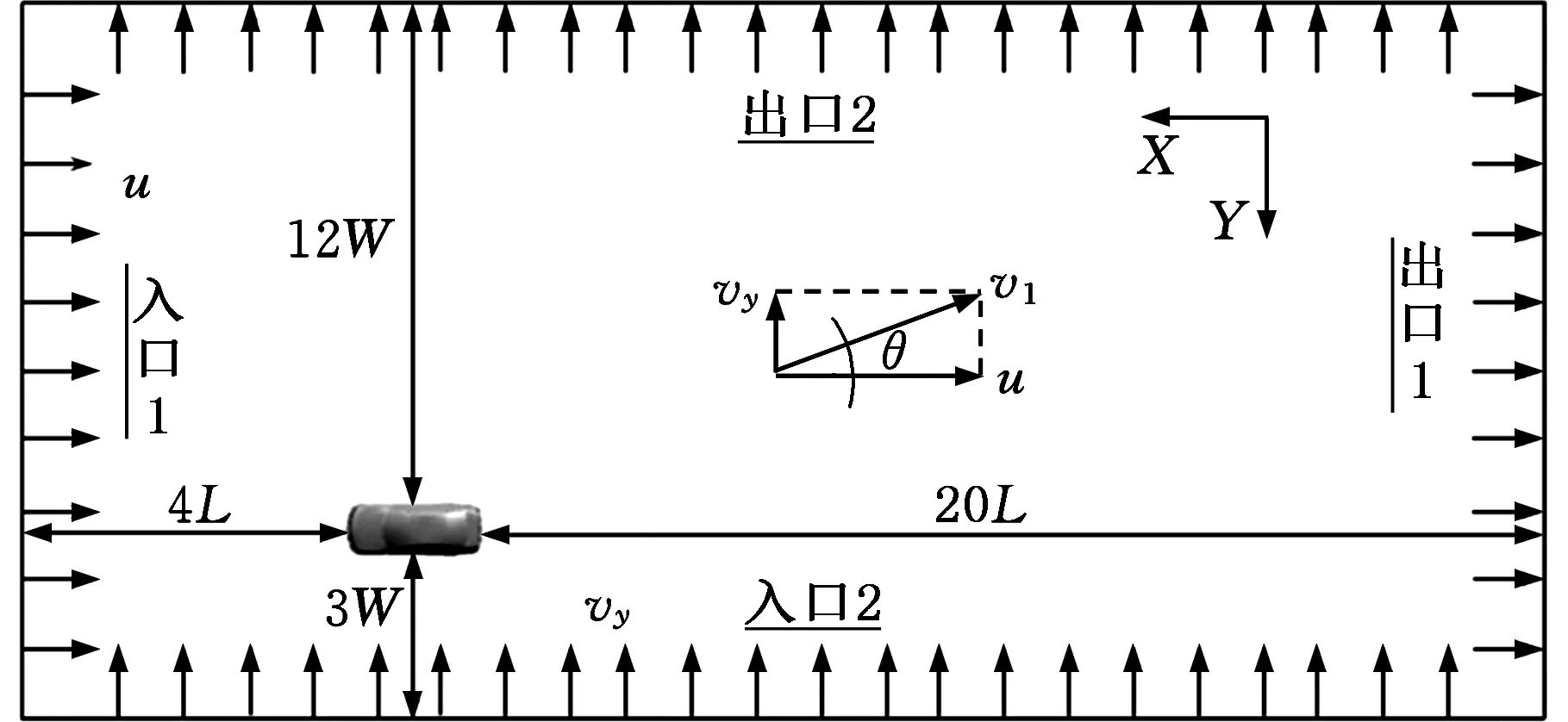
图5 静态耦合模拟方案Fig.5 Static coupling method simulation scheme

采用专业有限元软件将整个计算域生成四面体非结构化网格，在车身表面拉伸出3层棱柱网格模拟汽车表面的附面层，并且在计算敏感区域使用密度盒加密，以达到局部网格细化的目的[12]，纵对称面网格结构如图6所示。

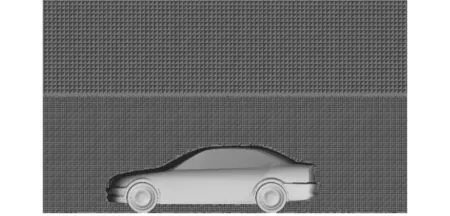
图6 纵对称面网格结构Fig.6 The mesh of longitudinal symmetry plane

结合本文所述的静态耦合方法,利用该静态侧风模拟方案进行汽车侧风稳定性问题的流体部分空气动力学仿真。

2.3 动态耦合方法

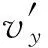
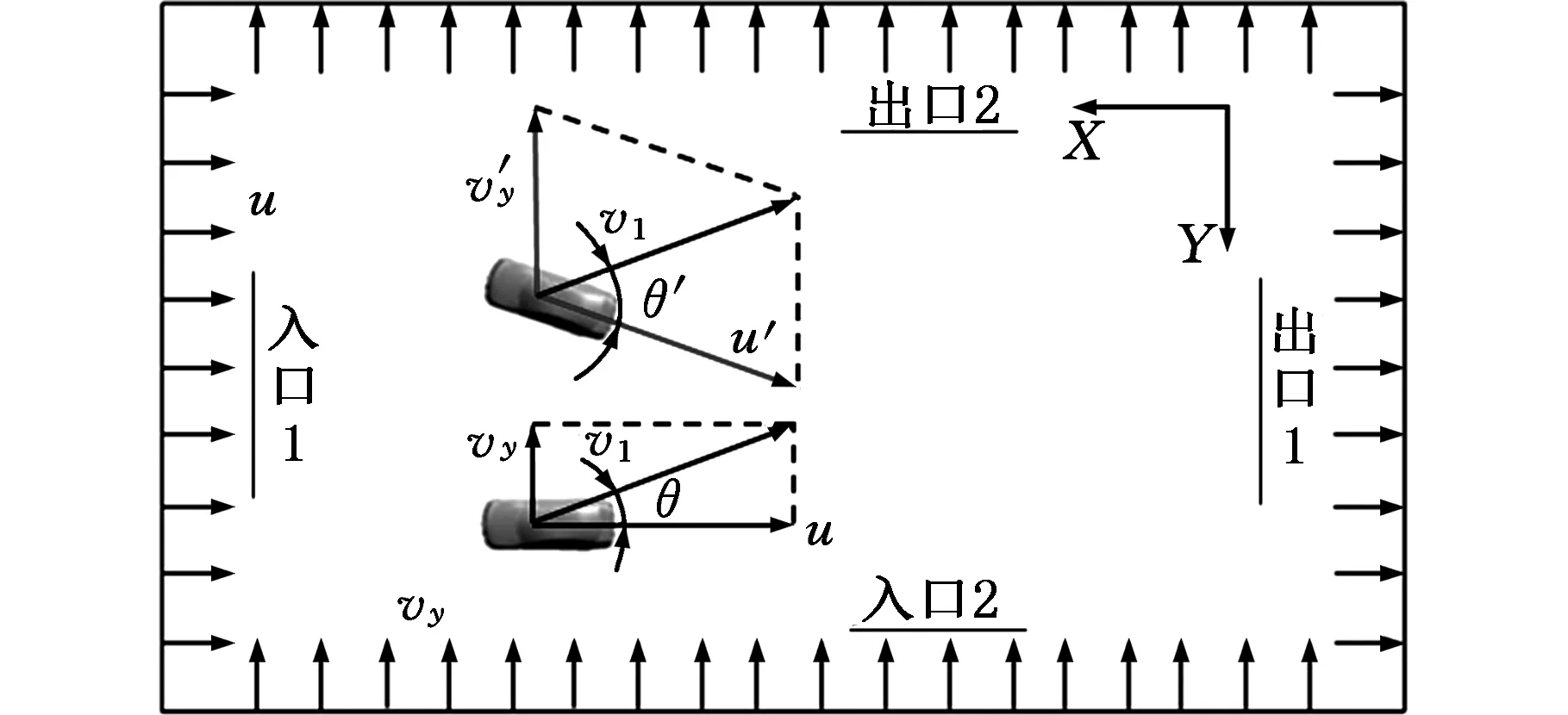
图7 静态模拟速度分析Fig.7 Velocity analysis of static simulation

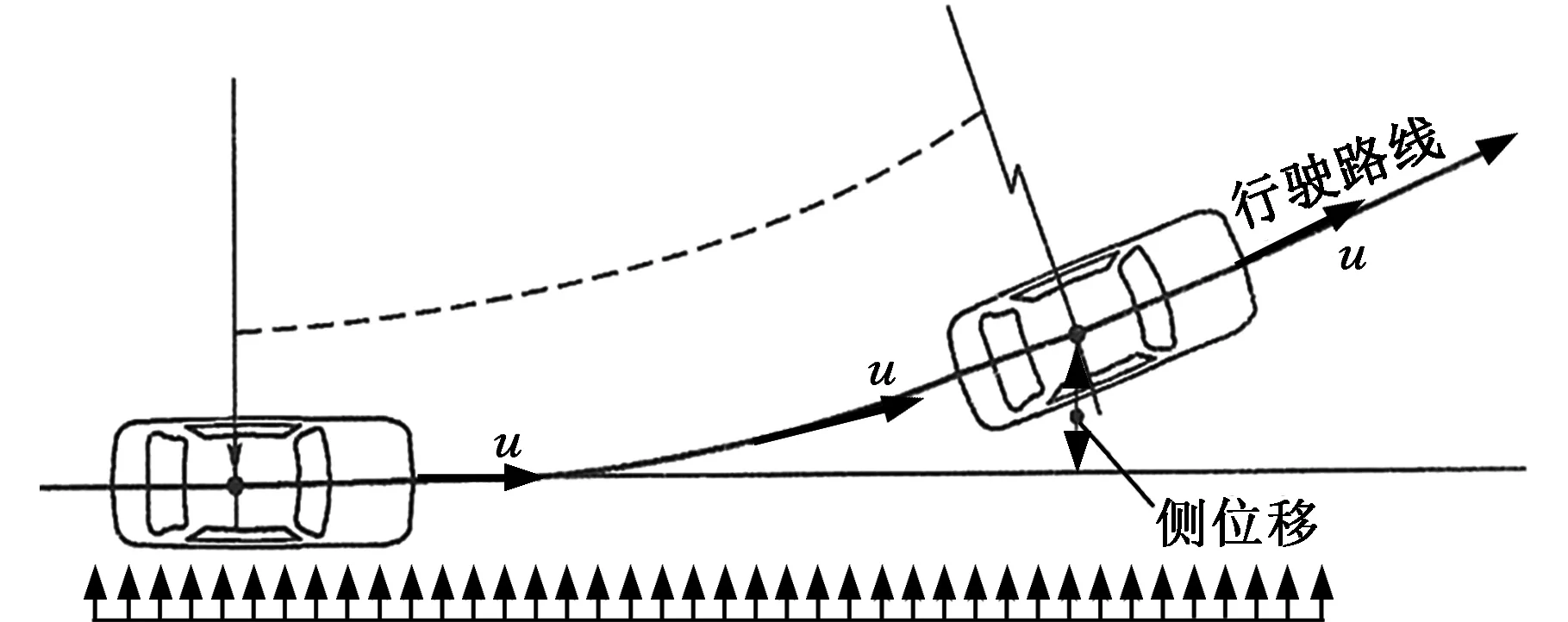
图8 侧风下汽车行驶路线示意图Fig.8 Vehicle route map by crosswind

基于此，本文提出了一种动态耦合方法，使汽车在计算域内以实际车速行驶，将车速与侧风独立开来，实现汽车侧风下的动态分析。模拟方案如图9所示。

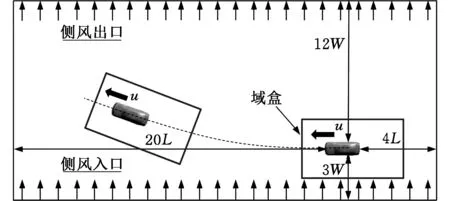
图9 动态耦合模拟方案Fig.9 Dynamic coupling method simulation scheme

该方案中车身壁面的运动由FLUENT动网格技术实现，但是由于车身表面较为复杂，附近网格尺寸较小，故壁面边界的运动势必会导致网格数量迅速增加，同时网格畸变率过大，甚至出现负体积，无法进行计算[13]。对于该情况，通常是将时间步长缩小，而这又将耗费大量的计算资源与时间，显然也不可取。

针对这一问题，本文采用了一种适合于模拟复杂运动边界大尺度运动的域盒动网格策略，即将汽车模型通过一长方体包裹，其内外两侧各建立网格区域，该长方体即为域盒[14]，如图10所示。边界条件设为Interior，在计算过程中，域盒内部的网格随汽车模型一起运动。该方法的最大优点是将网格更新的位置转移至域盒外面的大尺寸网格，而其内部小尺寸网格不再更新，其网格如图11所示。

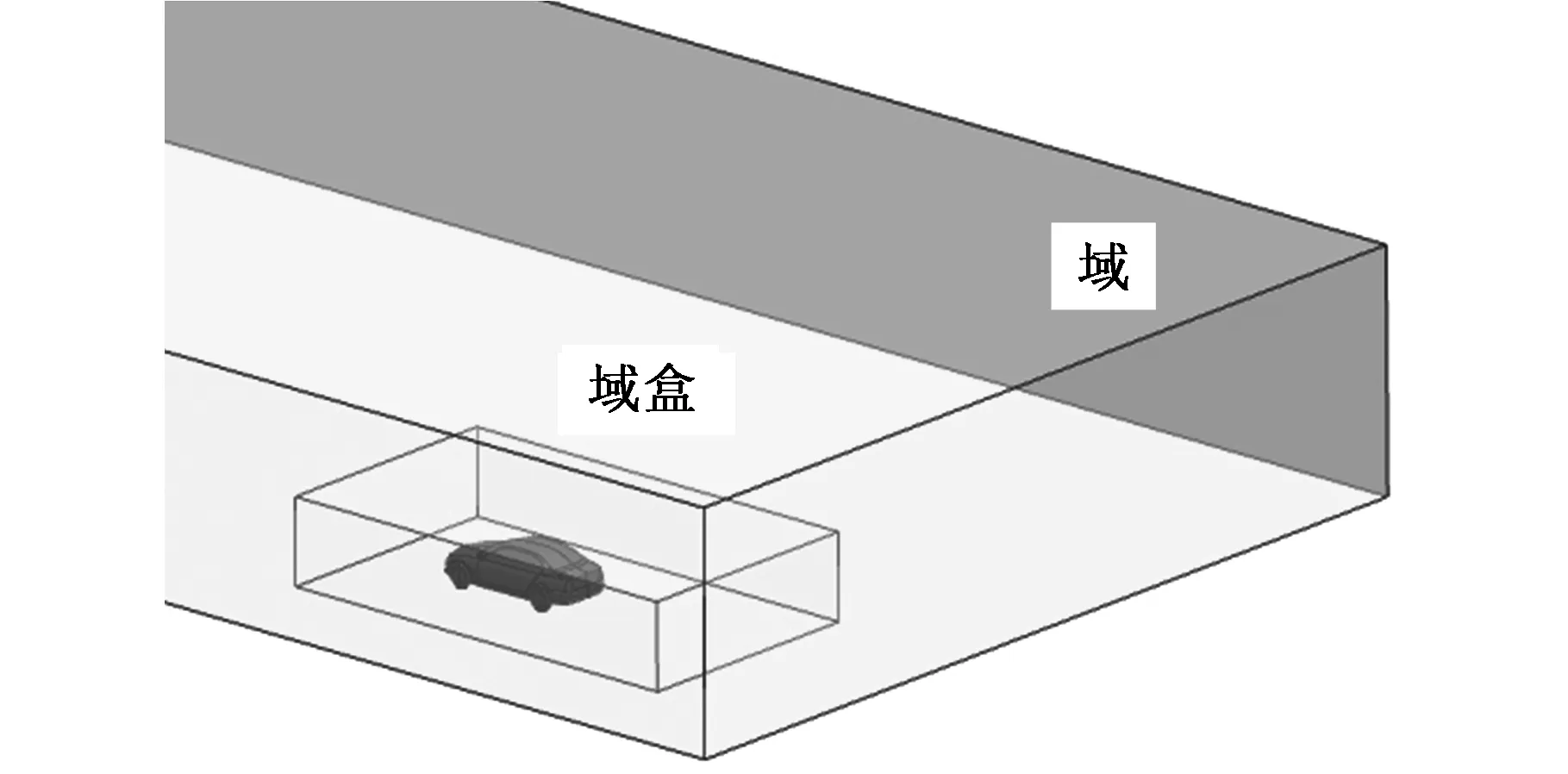
图10 域盒示意图Fig.10 Domain box diagram

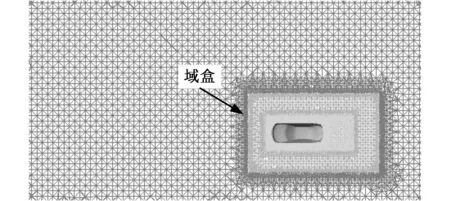
图11 动态模拟网格Fig.11 The mesh of dynamic coupling method

结合FLUENT中自定义函数(UDF)扩展功能，利用DEFINE_CG_MOTION函数及其变量实现对汽车整车运动的控制。静态耦合中主要定义了侧风速度vy与横摆角度速度ωr等变量；而动态耦合中主要定义了侧风速度vy与横摆角度速度ωr以及汽车行驶速度u等变量，从而实现对汽车侧风稳定性问题的动态耦合模拟。

3 动态、静态耦合对比研究

为了说明动静态耦合模拟对汽车侧风稳定性分析的区别，本节针对15 m/s侧风及30 m/s车速这一工况分别进行了两种仿真方法的对比研究，同时分别就其动力学响应中的侧向力、侧向速度与侧向位移等参数以及流场进行相关分析。

3.1 动力学响应对比

针对上述工况进行的动静态耦合仿真动力学响应如图12所示，由图12a可知，动态耦合中的汽车受侧风作用的侧向力较静态耦合的侧向力小(本文侧向力、侧向速度、侧向位移、横摆角的大小均指其绝对值)，且其减小速度较静态耦合快。侧向力的大小与相对速度(汽车相对于流场)的平方成正比，因此动静态耦合中相对速度均在减小，且动态耦合中相对速度减小较快。原因在于静态耦合中车速与侧风合速度v1不变，而侧风作用下汽车车身-Y方向的侧向速度逐渐增大，如图12b所示，所以其相对速度逐渐减小，侧向力逐渐减小；而动态耦合中车速与侧风合速度随汽车横摆而逐渐减小，且车身侧向速度较静态耦合大，因此其相对速度较静态耦合减小得快，侧向力变化趋势与之一致。

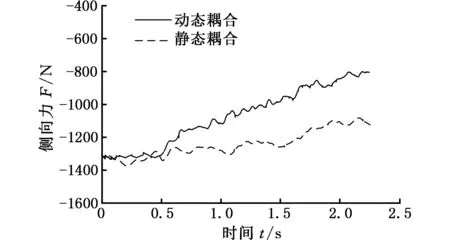
(a)侧向力

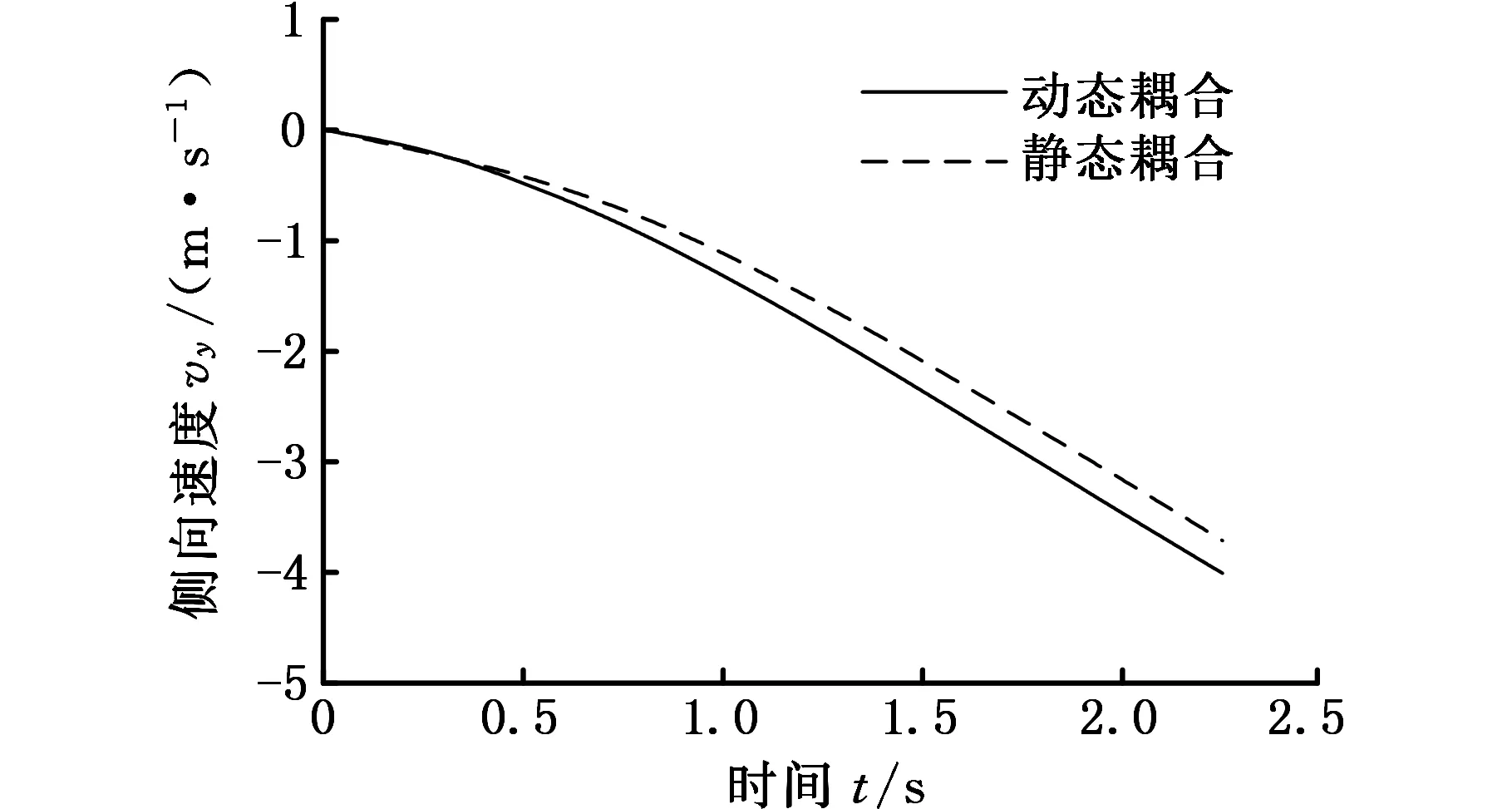
(b)侧向速度

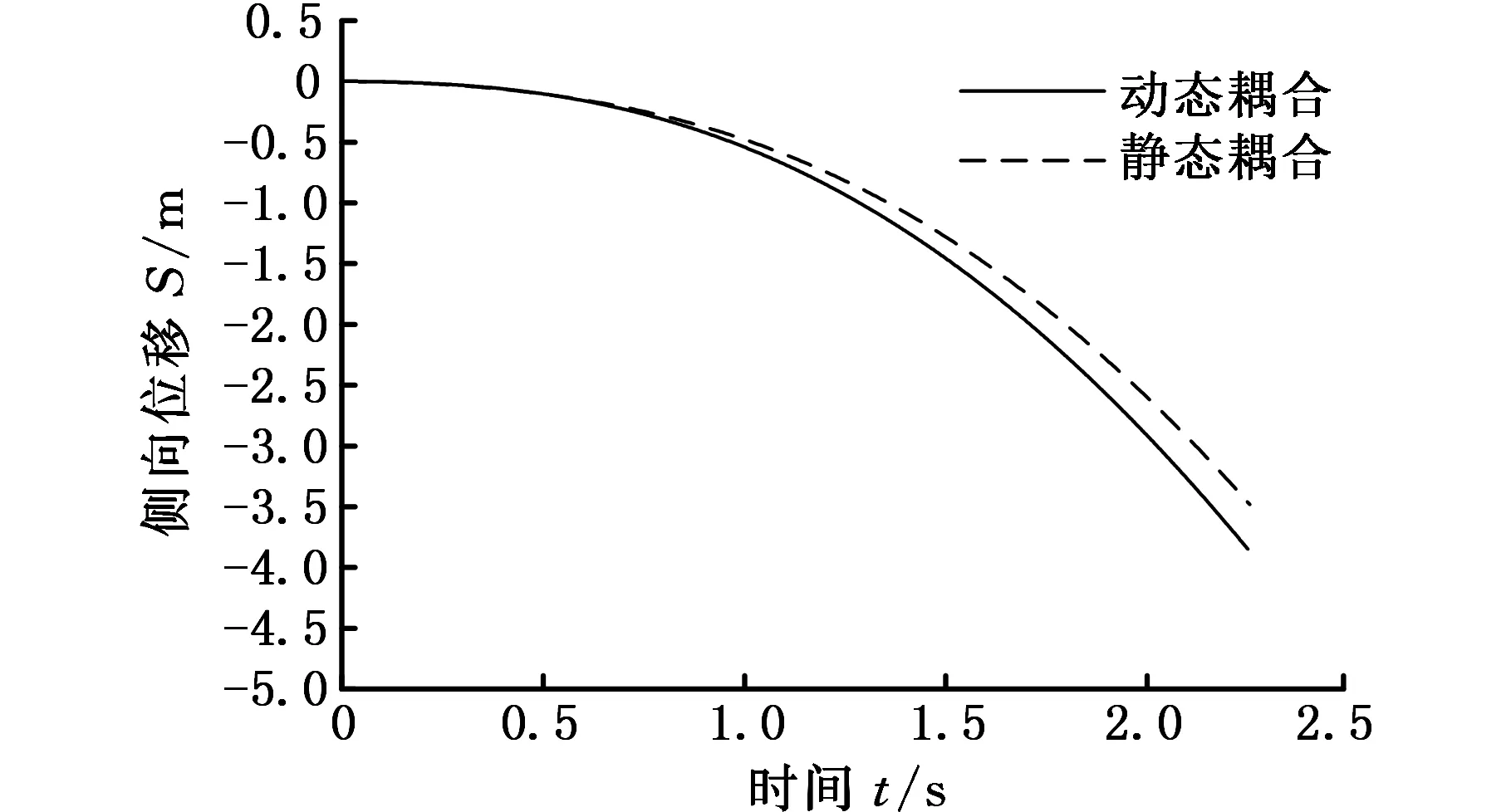
(c)侧向位移图12 动静态耦合对比Fig.12 The comparison of dynamic and static coupling

图12b为侧风作用下汽车的侧向速度与时间变化关系。动态耦合中汽车侧向速度较静态耦合大，其原因是动态耦合中汽车的侧向速度主要是由两部分组成，一部分是由侧向力所产生,另一部分是因为汽车横摆导致其车速在-Y方向上产生了一个速度分量。由于动态耦合侧向力较静态耦合小，导致由侧向力所产生的那一部分侧向速度减小，但车速在-Y方向的分量对于侧向速度的影响更为明显，从而导致动态耦合中汽车侧向速度较静态耦合大。

图12c为汽车受侧风作用下侧向位移随时间变化的关系。结合图12b速度曲线不难得出侧向位移与时间变化关系，由图12c可知动态耦合所得侧向位移明显较静态耦合大，15 m/s的侧风作用2.25 s的时间，其侧向位移相差了0.385 m，相比于静态耦合增大了11.12%。汽车侧风稳定性问题多以侧向位移作为评价指标[16]，因此动态耦合下的汽车侧风稳定性偏低。

3.2 流场对比

由图13流场速度云图可知，两者由于对车速模拟方法的不同导致流场速度存在明显区别：动态耦合中流场流速在15 m/s左右，而静态耦合流速在33 m/s左右；动态耦合中车身周围气体流速较快，而静态耦合恰好相反；动态耦合随着汽车在流场中行驶X方向位移发生变化,而静态耦合中X方向并未产生位移；动态耦合对应时刻的侧向位移较静态耦合大，这也从流场的角度验证了图12c中的结果。另外，动态耦合中汽车侧尾部的涡流区较静态耦合小，这主要是因为动态耦合中汽车以车速行驶导致侧尾部涡流区气体更新速度及涡的耗散加快的原因。

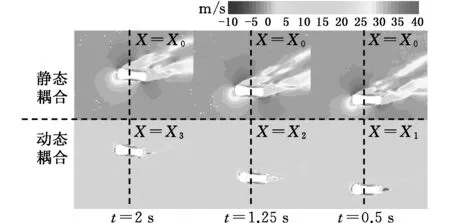
图13 各时刻速度云图Fig.13 Contour of velocity at different times

图14为t=2 s时刻车身表面压力云图，由图可知，此时静态耦合中车身迎风侧表面压力明显大于动态耦合迎风侧表面压力，且其背风侧表面压力较动态耦合小，由此可判断出t=2 s时刻，静态耦合中的气动力较动态耦合大，因此从车身表面压力的角度也定性地验证了图12中的气动力关系。

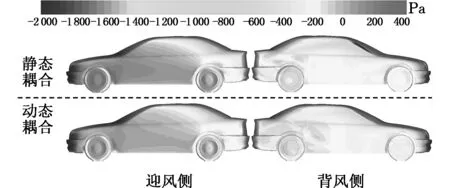
图14 车身表面压力云图(t=2 s)Fig.14 Contour of pressure on surface of vehicle(t=2 s)

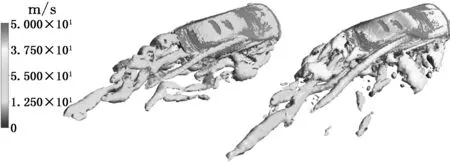
(a)动态耦合 (b)静态耦合图15 车身表面涡量图Fig.15 Contour of vorticity of vehicle

为了进一步说明两者在流场方面的区别，选取t=2 s时刻车身周围涡量云图，见图15。由涡量图可以看出漩涡产生的区域、大小以及漩涡表面气体的流速等信息。从图15中可知动态耦合中漩涡区小而短，而静态耦合中漩涡区大而长，并且由其表面气体流速可以看出静态耦合最外层气体流速较快，越接近车身表面气体流速越慢，动态耦合正好相反，越靠近车身表面气体流速越快，而最外层气体流速较慢，这进一步验证了图13速度场的分析。

通过以上动静态耦合中动力学和流场相关物理量及评价指标的对比分析可知，动态耦合中侧向位移相比于静态耦合增大了11.12%，其速度场、压力场以及涡量场等流场特性也有较大差异。因此，利用动态耦合仿真方法，真实地再现路面汽车与侧风的相互作用，提高模拟的准确性是十分必要的。

4 风速对稳定性的影响

本节主要利用动态耦合方法分析12 m/s、15 m/s及18 m/s三种不同侧风风速对汽车侧风稳定性的影响，其动力学响应如图16所示。

由图16a、图16b可知，在仿真初始阶段，侧风作用下汽车所受侧向力逐渐增大，至0.5 s左右达到最大，此后由于横摆角及侧向速度的增加，侧向力逐渐减小；而横摆力矩在0.5 s左右基本达到稳定。另一方面，随着侧风风速的增大，侧向力明显增大，而横摆力矩受侧风影响较小。

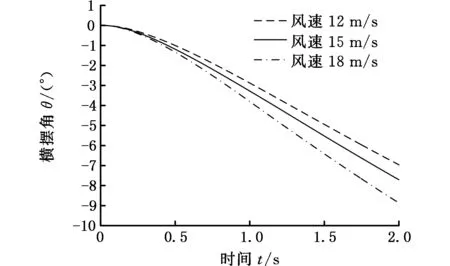
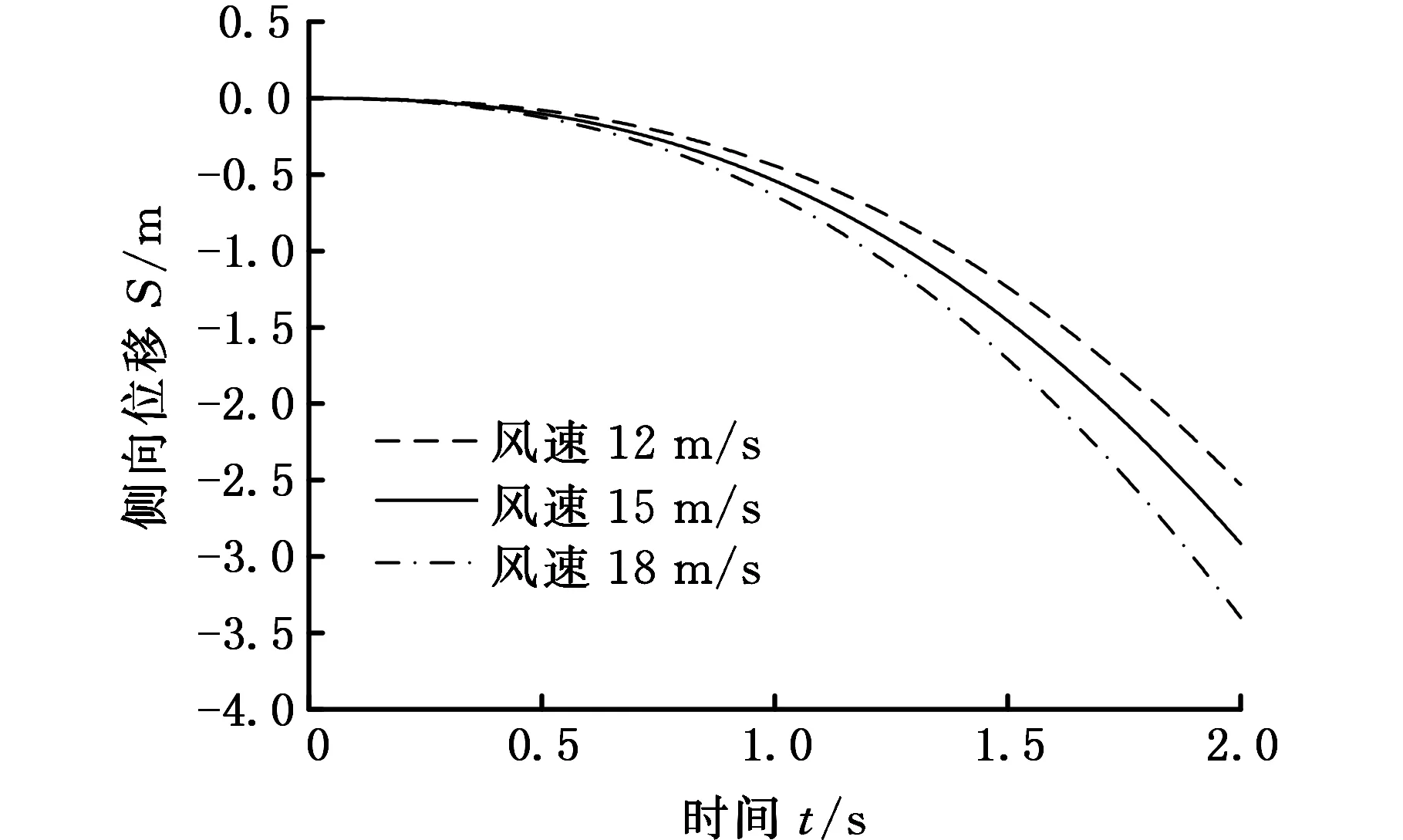
从运动学角度来看(图16c、图16d)，随着侧风风速的增加，横摆角及侧向位移均增大，其原因主要是气动力及力矩的增大，导致其对应方向上的速度增加，从而使得侧向位移和横摆角均增大。同样t=2 s时刻对比三种不同风速工况下横摆角及侧向位移，如表3所示，横摆角变化幅度分别为11.1%、14.6%，而侧向位移变化幅度分别为15.9%、16.2%，因此风速越高，对横摆角及侧向位移影响越大，且风速的变化同样对侧向位移的影响较横摆角明显。

从以上分析可知，不同侧风条件下，气动侧向力及横摆力矩、侧向位移及横摆角等均随侧风风速的增大而增大，且对侧向力和侧向位移影响较为明显。因此，随着侧风风速的增加，汽车侧风行驶气动稳定性降低。

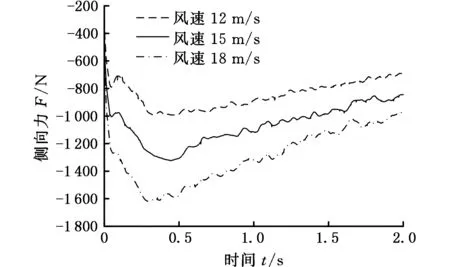
(a)侧向力

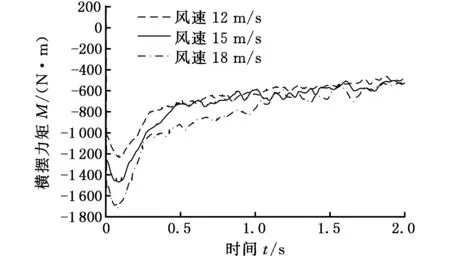
(b)横摆力矩

(c)横摆角

(d)侧向位移图16 风速对稳定性的影响Fig.16 The influence of wind velocity to vehicle

评价指标12m/s15m/s18m/s横摆角θ(°)-6.94-7.71-8.84侧向位移S(m)-2.51-2.91-3.38

5 结论

(1)对静态耦合方法进行了分析研究，就其对汽车侧风稳定性问题研究中的不足进行了说明，同时结合域盒动网格策略，提出了动态耦合仿真方法，并分析了其优势。

(2)通过动静态耦合对比研究发现，动态耦合下汽车侧风稳定性较静态耦合差，其侧向位移在文中工况下相比于静态耦合增大了11.12%。

(3)利用动态耦合对不同侧风风速进行了仿真分析，对于文中工况，随侧风风速增大横摆角变化幅度分别为11.1%、14.6%，侧向位移变化幅度分别为15.9%、16.2%，因此风速越高，汽车侧风稳定性越差。

参考文献：

[1] 谷正气. 汽车空气动力学[M]. 北京: 人民交通出版社,2005:90-101.

GU Zhengqi. Automobile Aerodynamic[M]. Beijing: China Communications Press,2005:90-101.

[2] 王夫亮. 侧风作用下汽车气动特性研究[D]. 长春: 吉林大学,2009.

WANG Fuliang. Research on Automobile Aerodynamic Characteristics in Crosswind[D]. Changchun: Jilin University,2009.

[3] KOBAYASHI N, YAMADA M.Stability of a One Box Type Vehicle in a Cross-wind—an Analysis of Transient Aerodynamic Forces and Moments[J]. SAE Technical Paper,1988，881878.

[4] 谷正气, 丰成杰, 陈阵, 等. 汽车侧风稳定性的双向耦合方法研究[J]. 北京理工大学学报, 2016,36(9):923-928.

GU Zhengqi, FENG Chengjie, CHEN Zhen, et al. Research on the Two-way Coupling Method for Vehicle in Crosswind Condition[J]. Journal of Beijing Institute of Technology,2016,36(9):923-928.

[5] 杨滨徽. 隧道内复杂工况下汽车高速气动特性研究[D]. 长沙: 湖南大学,2010.

YANG Binhui. Research on Aerodynamic Characteristic of High Speed Vehicles in Complicated Traffic in Tunnel[D]. Changsha: Hunan University,2010.

[6] 黄泰明, 谷正气, 丰成杰, 等. 不同波长瞬态侧风对汽车气动性能影响分析[J]. 中国机械工程,2016,27(22):3111-3117.

HUANG Taiming, GU Zhengqi, FENG Chengjie, et al.Analysis for Effects of Transient Crosswinds with Different Wave-lengths on Vehicle's Aerodynamics Performance [J]. China Mechanical Engineering,2016,27(22):3111-3117.

[7] 孙露. 计及侧风的某跑车高速气动稳定性研究[D]. 长沙: 湖南大学,2011.

SUN Lu. Research on Automotive Aerodynamic Characteristics and Stability in Crosswinds[D]. Changsha: Hunan University,2011.

[8] 余志生. 汽车理论[M]. 5版. 北京: 机械工业出版社,2010:144-146.

YU Zhisheng. Automobile Theory[M]. 5th ed. Beijing: China Machine Press,2010:144-146.

[9] 贺桂敏. 某集装箱货车高速侧风气动特性优化研究[D]. 长沙: 湖南大学,2013.

HE Guimin. Analysis and Optimization of High Speed Aerodynamic Characteristics of a Container Truck in Crosswinds [D]. Changsha: Hunan University,2013.

[10] 于勇. FLUENT入门与进阶教程[M]. 北京: 北京理工大学出版社,2008.

YU Yong. Tutorial of FLUENT Introduction and Advanced[M]. Beijing: Beijing Institute of Technology Press,2008.

[11] 张德丰. MATLAB与外部程序接口编程[M]. 北京: 机械工业出版社,2009:95-103.

ZHANG Defeng. MATLAB with External Interface Programming[M]. Beijing: Mechanical Industry Press,2009:95-103.

[12] 海贵春, 谷正气, 王和毅, 等. 侧风对汽车高速行驶性能影响的仿真研究[J]. 湖南大学学报,2006,33(2):40-43.

HAI Guichun, GU Zhengqi, WANG Heyi, et al. Research on the Effect of Crosswinds on the Stability of High Speed Vehicles[J]. Journal of Hunan University,2006,33(2):40-43.

[13] 陈阵, 谷正气, 张勇, 等. 汽车雨刮器的瞬态气动特性[J]. 中南大学学报,2016,47(10):3597-3604.

CHEN Zhen, GU Zhengqi, ZHANG Yong, et al. Transient Aerodynamic Characteristics of Windscreen Wipers of Vehicles [J]. Journal of Central South University,2016,47(10):3597-3604.

[14] 谭鹏, 谷正气, 陈阵, 等. 汽车刮水器气动升力的风洞试验及数值研究[J]. 空气动力学学报,2016(3):345-352.

TAN Peng, GU Zhengqi, CHEN Zhen, et al. The Experimental and Numerical Research on Aerodynamic Lift of Automobile Wind Shield Wiper[J]. Journal of Aerodynamics,2016(3):345-352.