动车组受电弓系统失效风险分析

齐金平 李兴运

1.兰州交通大学机电技术研究所， 兰州，7300702.甘肃省物流及运输装备信息化工程技术研究中心，兰州，730070

0 引言

受电弓系统作为动车组的重要系统，连接着动车组车体和接触网，从接触网上获取电能为动车组提供动力。目前所有动车组受电弓均开放式地安装在动车组顶部且使用频繁，容易发生故障,所以对受电弓系统进行失效风险分析，找到影响系统失效的主要因素，对保证动车组安全运营具有重要意义。

目前对动车组受电弓系统进行失效风险分析的研究较少，但在隧道地铁施工、海底管道和航空等方面的风险分析已经有了较为成熟的研究。EINSTEIN[1]首次提出对隧道以及地下施工进行风险分析，并对其应用前景进行了阐述。随后失效风险分析很快在其他工程方面得到了应用。李新宏等[2]利用贝叶斯网络对海底石油管道泄漏事件进行了风险分析，并对其故障概率进行预测，找出了容易导致石油管道泄漏的薄弱环节。周健等[3]针对地铁盾构法施工展开研究分析，根据专家调查和事故的先验概率建立了多态贝叶斯网络风险分析评估模型，得到了施工风险概率等级，但贝叶斯网络建模和计算困难。郭媛媛等[4]结合故障模式、故障后果分析和故障树分析对飞机进行风险分析，得到了飞机风险变化趋势，并提出了合理化的建议，从而降低了飞机的运行风险。在动车组风险分析方面，贾潞[5]利用历史数据对受电弓故障进行了分类，并建立故障树对受电弓进行了定量和定性分析；刘敬辉[6]结合FMECA和故障树分析方法对动车组空气弹簧悬挂系统进行了安全风险分析，并根据分析结果提出了风险控制措施。故障树分析法过分依赖大量的历史数据，且故障机理清晰，而在实际应用中，很多系统存在历史数据缺乏、多源异构和故障机理不清晰的问题，从而限制了故障树的推广使用。

本文利用故障树构建模糊贝叶斯网络对受电弓失效风险进行分析，计算影响受电弓系统失效的各事件敏感度，找出对系统失效影响较大的节点，并根据分析结果提出合理化的建议来降低受电弓的失效风险。该方法融合了故障树和贝叶斯网络在风险分析方面各自的优点，综合考虑了受电弓系统故障数据的缺失和多源异构情况，简化了计算过程。对受电弓系统进行实例分析，找出了导致受电弓运营过程中失效的薄弱环节，再结合实际情况提出了合理化的建议来提高系统的可靠性。

1 贝叶斯网络及其建模过程

1.1 贝叶斯网络

贝叶斯网络[7-8](Bayesian network,BN)是一个有向无环图(directed acyclic graph, DAG),它由代表变量的节点和有向边构成。每个节点代表一个变量，有向边用于连接节点，定性地表示变量间的关联关系。条件概率表由不同情况下的条件概率组合而成，定量地描述变量间的关联关系。在风险分析过程中，贝叶斯网络能够很好地处理故障机理不清晰问题，其计算方便，从而能够对多态系统进行表达，但建模困难。

1.2 T-S模糊故障树

T-S模糊故障树[9]为T-S模糊理论和故障树相结合的一种方法。在风险分析过程中，使用模糊可能性对系统各事件故障概率进行描述，解决了由于历史数据缺失和多源异构情况造成的故障概率不精确的问题；使用模糊数对故障程度进行描述，克服了一般分析过程中故障程度难以定量分析的困难；构建T-S模糊门规则，能够对各事件之间的逻辑关系进行表达，解决了故障机理不清晰的问题。所以T-S模糊故障树能够在数据缺失和多源异构的情况下对多态系统进行分析，但是存在计算复杂，不能逆向推理的缺点。

1.3 T-S模糊故障树构建贝叶斯网络模型

本文综合T-S模糊故障树和贝叶斯网络在风险分析方面的优缺点，利用T-S模糊故障树构建模糊贝叶斯网络风险分析模型。在故障数据缺失和多源异构的情况下，对多态受电弓系统进行失效风险分析， 具体构建过程如下：①将T-S模糊故障树转化为贝叶斯网络的有向无环图，其中T-S模糊故障树中各事件分别与贝叶斯网络中各节点相对应，如基本事件对应根节点、中间事件对应中间节点、顶事件对应叶节点，且分别用有向边按照对应关系相连接；②将T-S模糊故障树中模糊门规则转化为贝叶斯网络中的条件概率表，由于模糊门规则符合条件概率和独立性要求，所以可直接转换，当面对复杂多态系统时可以根据情况对模糊贝叶斯网络进行节点状态的扩充。

表1 T-S模糊门规则Tab.1 T-S fuzzy gate rule

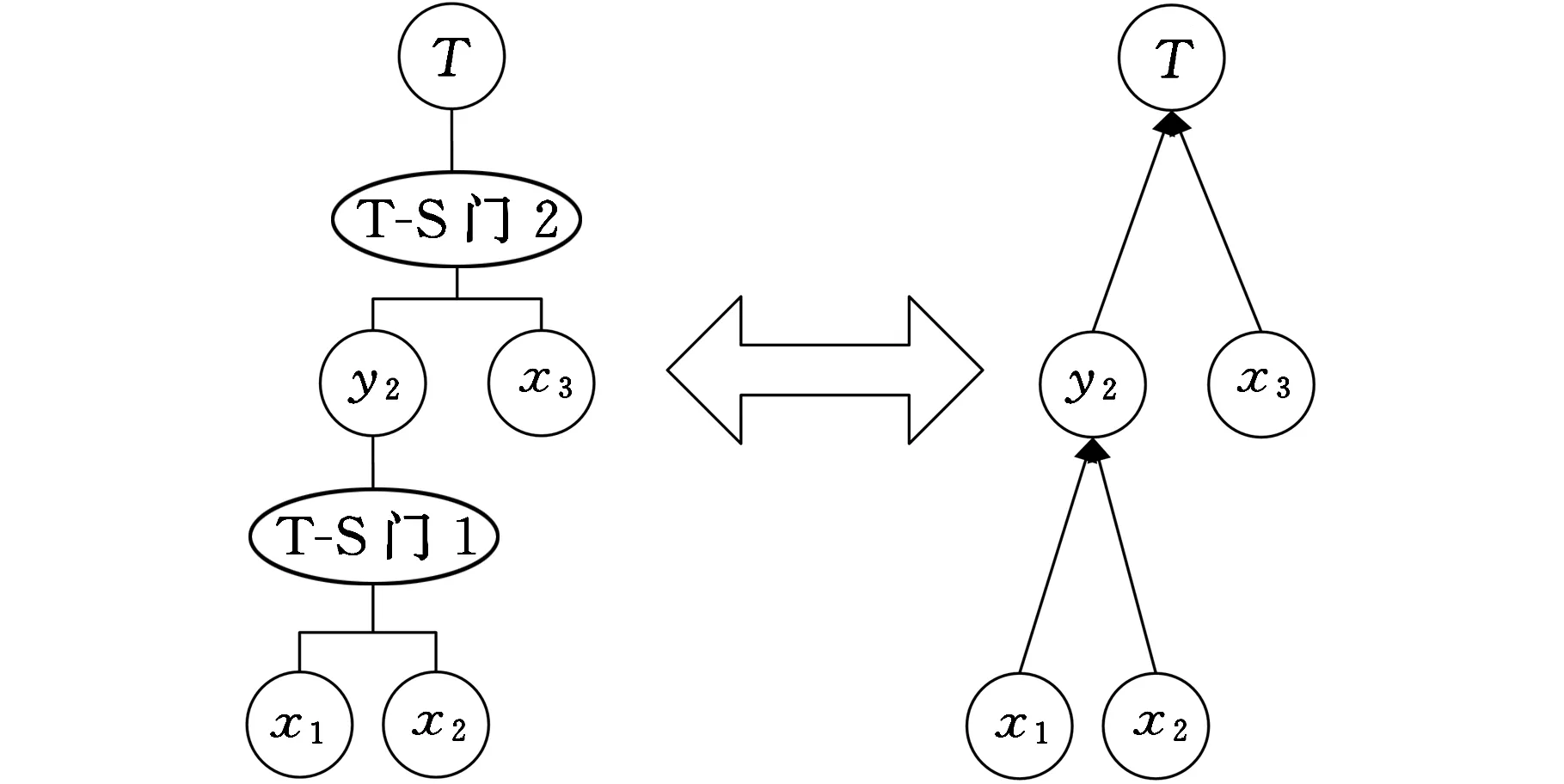
图1 T-S模糊故障树映射为BN有向无环图的过程Fig.1 T-S fuzzy fault tree is mapped to the BN process of acyclic graph

根据表1可以得出BN中对应节点y的条件概率为

(1)

(2)

同理可得叶节点T的条件概率。传统的二态系统常把系统和基本部件的故障状态描述为正常和故障两种状态，而在实际应用中，系统和部件往往呈现出多种故障状态，比如一些基本事件的发生并不能导致顶事件故障的直接发生，可能导致系统处于轻微故障阶段。因此，本文用模糊数(0,0.5,1)分别来描述系统三种故障状态(无故障、轻微故障、故障)，由上述T-S模糊故障树映射为BN的过程可以看出，在对受电弓的失效风险分析过程中可使用贝叶斯网络对受电弓的多态性进行描述。

2 叶节点的故障概率和根节点的灵敏度

2.1 叶节点的故障概率

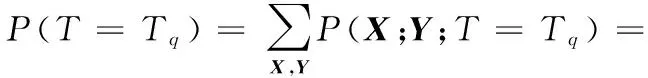
(3)

其中，λ(T)为叶节点T的父节点集合;λ(yj)为中间节点yj的父节点集合。

2.2 根节点的灵敏度

灵敏度反映的是根节点对叶节点故障状态的敏感性，对其进行分析可得根节点变量的分布参数对叶节点可靠性的影响关系，可以在根节点的故障状态变化较小的情况下使得叶节点可靠性差值较大，从而能够找出影响系统失效的高风险事件，为建立风险控制提供理论依据。

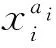
(4)

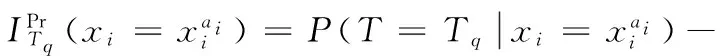
(5)

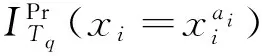
由式(4)和式(5)可得根节点xi对叶节点T故障状态为Tq的灵敏度为

(6)

3 结合受电弓实例分析

以文献[10]中多态受电弓系统为例进行分析，BN中各节点分别与受电弓T-S模糊故障树中各事件相对应，BN分析数据均来源于文献中，根据兰新动车组上线运营以来故障数据整理得出各基本部件的故障率来进行分析。将受电弓T-S模糊故障树映射为模糊BN模型(具体映射过程见文献[11])，如图2所示。

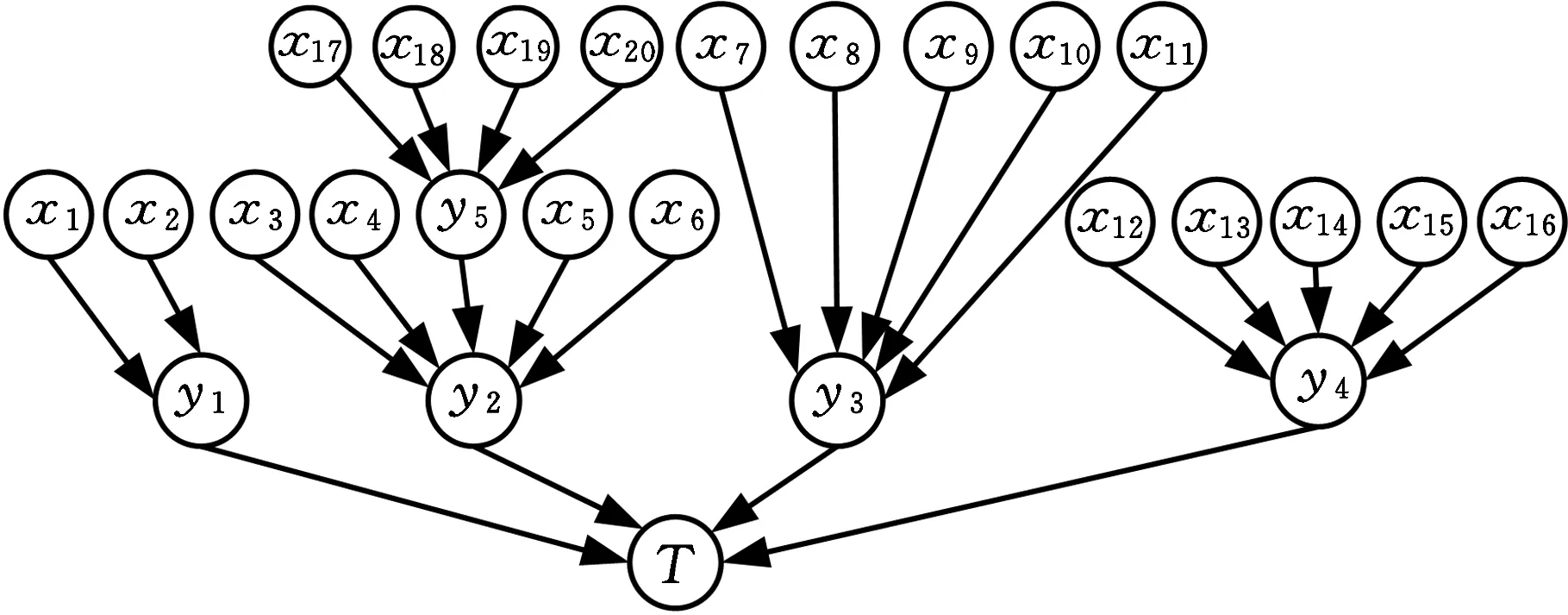
图2 多态受电弓系统模糊贝叶斯网络Fig.2 Fuzzy BN model for multi pantograph system

图2中，x1，x2，…，x20为根节点(基本事件)，T为叶节点(顶事件)，y1、y2、y3、y4和y5为中间节点(中间事件)。表2所示为各个节点代表的具体含义。

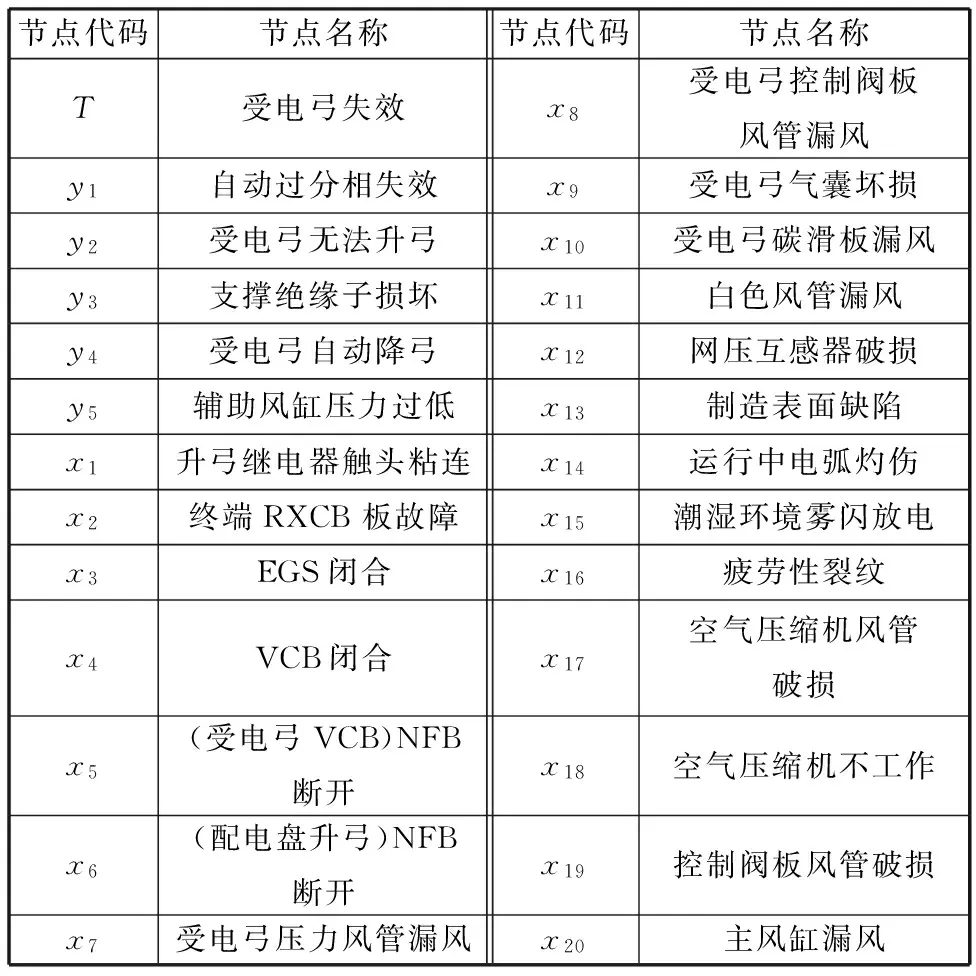
表2 受电弓模糊BN模型中各节点含义Tab.2 The meaning of each node in the fuzzyBN of pantograph

各根节点的故障数据来源于兰新客运专线故障数据统计以及基于信心指数修正的专家调查法得出，为三角形模糊数,其模糊故障率见表3。

根据T-S模糊故障树构建模糊贝叶斯网络过程的数据来源于兰新客运专线故障数据统计以及基于信心指数修正的专家调查法得出。中间节点y1的条件概率表见表4。

表3 受电弓各基本事件的模糊故障率Tab.3 Fuzzy failure rate of each basic event ofpantograph 10-7

表4 中间节点y1的条件概率Tab.4 Conditional probability of intermediate node y1

表4中，规则4表示在x1、x2同时发生故障的情况下，中间事件y1发生不确定故障的概率为0，发生故障的概率为1，即当升弓继电器触头粘连和终端RXCB 板故障同时发生时，自动过分相失效一定发生。其他节点的条件概率表参考文献[10]。

利用式(1)和式(2)，并结合贝叶斯网络可以求得各中间节点的模糊可能性，如表5所示。

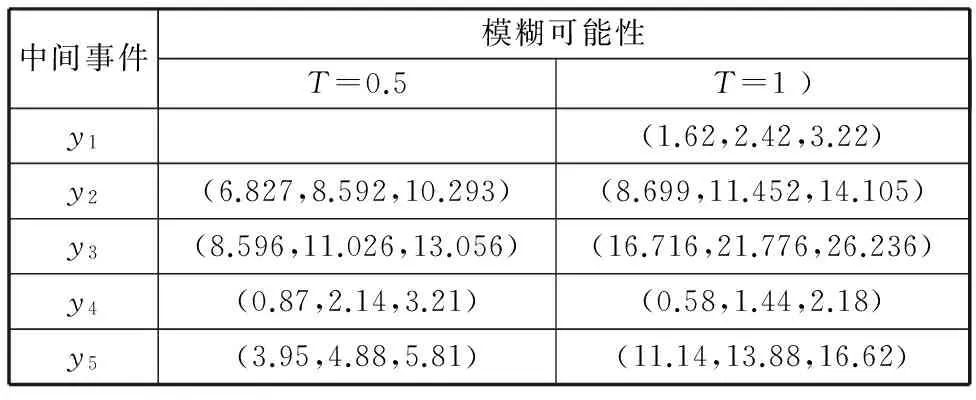
表5 中间节点模糊可能性Tab.5 Fuzzy possibility of intermediate event 10-7

同理经过计算可得叶节点T的模糊可能性：

P(T=0.5)=(11.01，14.881，18.266)×10-7

P(T=1)=(30.354，40.358，49.488)×10-7

由叶节点的模糊可能性计算公式可知，叶节点的模糊可能性和各根节点的模糊故障率为一个数量级，与现场实际情况相符合。

利用式(4)可以求出各根节点在故障状态为0.5和故障状态为1时的灵敏度，如表6所示。

利用式(6)可以求出各根节点的灵敏度如表7所示。

根节点的灵敏度描述了系统基本事件发生故障状态变化时对系统故障的发生造成的影响。对系统进行灵敏度分析，可以在根节点变化很小的情况下使系统可靠性差值很大，从而能够找出影响系统可靠性的高风险事件。由表7可知，x12、x16、x19等为影响系统可靠性的高风险事件，在检修和管理过程中应该重点关注这些事件，虽然x13(制造表面缺陷)的灵敏度很大，但不属于高风险事件，因其制造表面缺陷的模糊故障率为0，即小概率事件。部件从制造到使用都经过多层筛选，又因为是小概率事件所以认为是低风险事件,符合实际情况。x12(网压互感器破损)、x16(疲劳性裂纹)、x19(控制阀板风管破损)为高风险事件，由于受电弓为开放式地安装在动车组顶部，容易受到异物击打而造成损坏，且由我国动车组运营单线运营里程长、上线率高的实际情况可知，部件易产生疲劳性裂纹，所以当上述部件发生故障状态的变化时，受电弓系统故障造成的影响较大，认为是高风险事件,与实际情况一致，从而验证了分析结果的正确性。

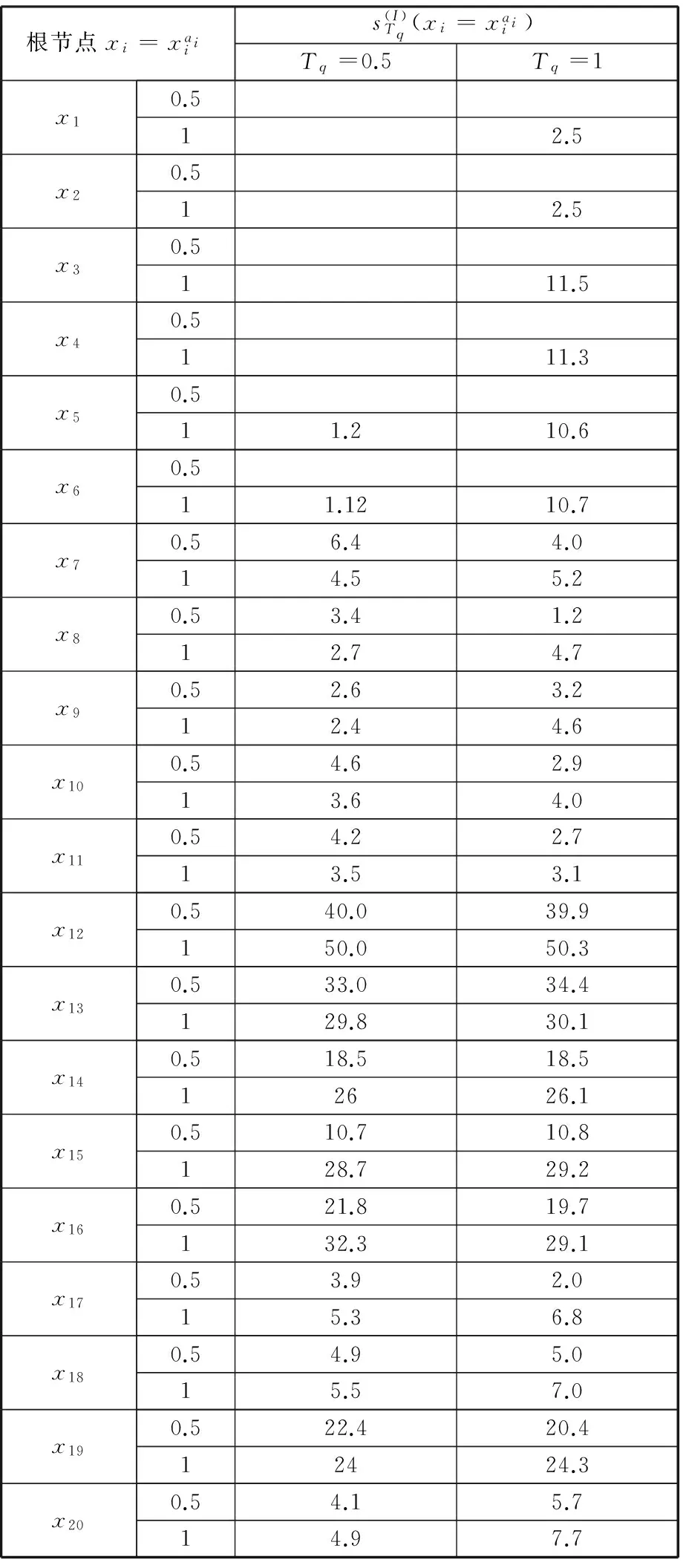
表6 各根节点不同故障状态的灵敏度Tab.6 Sensitivity of each root node with differentfault states 105

表7 各根节点的灵敏度Tab.7 Sensitivity of each root node 105

4 结论

(1)在对受电弓系统失效风险分析中，存在历史故障数据多源异构、数据缺失和认知不确定的实际情况，利用模糊故障树构建多态模糊贝叶斯网络对其进行分析，可解决系统失效分析过程中因为数据的不完整而难以进行建模分析的困难;计算出了各中间节点和叶节点的模糊可能性，并利用各根节点的灵敏度来反映影响系统可靠性的高风险事件，分析结果与实际情况相一致。

(2)利用故障树构建贝叶斯网络对系统的失效风险分析，简化了贝叶斯网络的构建过程，同时降低了其计算的复杂程度，扩展了其在实际工程中的分析应用。

参考文献：

[1] EINSTEIN H H, VICK S G. Geological Model for Tunnel Cost Model [J]. Proc. Rapid Excavation and Tunneling Conf.,1974(2):1701-1720.

[2] 李新宏,朱红卫,陈国明,等. 海底油气管道泄漏事故风险分析的贝叶斯动态模型[J]. 中国安全科学学报,2015,25(4):75-80.

LI Xinhong, ZHU Hongwei, CHEN Guoming, et al. Bayesian Dynamic Model for Analyzing Risk of Meeting Submarine Oil & Gas Pipeline Leakage Accident[J]. China Safety Science Journal,2015,25(4):75-80.

[3] 周健,王红卫,吴邵海. 盾构法施工风险的多态贝叶斯网络模型分析[J]. 同济大学学报(自然科学版),2013,41(2):186-190.

ZHOU Jian,WANG Hongwei,WU Shaohai. Risk Analysis of Shield Construction by Polymorphic Bayesian Networks Model[J].Journal of Tongji University(Natural Science Edition),2013,41(2):186-190.

[4] 郭媛媛,李龙彪,胡宇群,等. 民用飞机运行风险评估方法[J]. 航空工程进展,2016,7(2):253-258.

GU Yuanyuan, LI Longbiao, HU Yuqun, et al. Operation Risk Assessment Method of Civil Aircraft[J]. Advances in Aeronautical Science and Engineering,2016,7(2):253-258.

[5] 贾潞. 基于风险管理的动车组受电弓故障树分析[D].西南交通大学,2015.

JIA Lu. Fault Tree Analysis of EMU Pantograph Based on Risk Management[D].Chengdu: Southwest Jiaotong University,2015.

[6] 刘敬辉. 高速动车组空气弹簧悬挂系统安全风险分析及控制研究[J]. 铁道运输与经济,2017,39(1):66-70.

LIU Jinghui. Safety Risk Analysis and Risk Control Research on Air Spring Suspension System of High-speed EMU[J]. Railway Transport and Economy,2017,39(1):66-70.

[7] PEARL J F. Propagation and Structuring in Belief Networks [J]. Artificial Intelligence,1986,29(3):241-248.

[8] JENSEN F V. An Introduction to Bayesian Networks [M].New York: Springer,1996.

[9] 宋华,张洪钺,王行仁. T-S模糊故障树分析方法[J]. 控制与决策,2005,20(8):854-859.

SONG Hua, ZHANG Hongyue, WANG Xingren. Fuzzy Fault Tree Analysis Based on T-S Model[J]. Control and Decision,2005,20(8):854-859.

[10] 李兴运,齐金平. 基于T-S模糊故障树的受电弓系统可靠性分析[J].安全与环境学报,2018,18(1):33-38.

LI Xingyun, QI Jinping. Reliability Analysis of Pantograph System Based on T-S Fuzzy FTA[J]. Journal of Safety and Environment,2018,18(1):33-38.

[11] 李盼,樊建春,刘书杰. 基于故障树与贝叶斯网络的钻井井塌事故的定量分析[J]. 中国安全生产科学技术,2014,10(1):143-149.

LI Pan, FAN Jianchun, LIU Shujie. Quantitative Analysis of Borehole Collapse in Drilling Base on Fault Tree Analysis and Bayesian Networks[J]. Journal of Safety Science and Technology,2014,10(1):143-149.