PDC钻头切削断面对破岩效率的影响
2018-04-24祝效华易勤健
祝效华 易勤健
西南石油大学机电工程学院,成都,610500
0 引言
在油气勘探开发过程中,PDC(polycrystalline diamond compact)钻头凭借其钻速高、寿命长和成本低等特点得到了广泛应用。相对于牙轮钻头的冲击、压碎破碎岩石,PDC钻头通过固定PDC齿剪切破碎岩石显然更加有效。然而,随着钻探活动向深部硬地层钻进,PDC钻头并不能发挥其最大性能。以往的研究认为,影响PDC钻头破岩效率的因素除了钻井参数和地层岩性外,PDC齿的空间布置参数也是一个重要因素[1]。
当前,国内外学者对PDC钻头布齿进行了相关研究。HIBBS等[2]通过试验得到了8.13 mm切削齿切削砂岩的最优后倾角在10°~20°范围内。梁尔国等[3]利用改装后的车床模拟了切削齿的不同切削断面形状、重复切削状态及磨损状态,并对多种岩样进行了切削齿的试验研究,研究认为切削面积相同的情况下,切削齿受力随接触弧长呈线性变化趋势,其切削齿受力最小的后倾角在5°~10°范围内。RAJABOV等[4]对PDC齿在大气压及围压下切削大理岩、页岩和砂岩的研究中得到,切削相同体积的岩石,小后倾角所需要的水平切削力较小,表明PDC钻头在较小后倾角下可以有更高的钻速,同时在相同转速下也有更小的扭矩。HARELAND等[5]定义了PDC单齿切削效率为单位力切削的体积,并推导出切削效率为后倾角、切削深度和岩石属性的函数,其切削齿的最优后倾角在0°~25°范围内,建议切削深度为1~1.5 mm。MARTINEZ等[6]通过有限单元法建立了单齿切削蒸发岩的仿真模型,并用机械比能评价了齿的切削深度、齿的几何结构以及围压对破岩效率的影响。CARRAPATOSO等[7-8]通过离散单元法对PDC齿的后倾角和切削深度进行了分析,研究认为较小的后倾角有利于提升切削效率,其中齿的最优切削深度在0.8~1.6 mm范围内,而增大齿与岩石表面的粗糙度将降低切削效率。祝效华等[9]利用有限元建立了PDC切削齿动态破岩的三维仿真模型,分析了后倾角、侧倾角、切削深度和围压等因素对破岩能效的影响。
综上所述,虽然针对PDC齿切削岩石的研究很多,也有很多关于切削齿在PDC钻头上布置方式的建议,但是,上述研究大都未考虑切削断面对PDC齿破岩效率的影响。在实际切削过程中,PDC钻头受布齿密度的影响,切削齿的切削断面会发生较大变化,因此分析PDC齿的典型切削断面十分重要,针对不同切削断面进行切削齿空间布置也具实际意义。本文基于弹塑性力学和岩石力学,以Drucker- Prager准则作为岩石的本构关系,建立了PDC齿动态破岩的非线性动力学三维有限元模型,主要针对3种典型切削断面,研究了不同围压下,切削断面的面积、切削齿的后倾角及侧转角对切削齿破岩效率的影响。
1 数值模型的建立
为方便说明切削断面的影响,将3种典型切削断面用图1表示[10]。切削断面A(单一重复切削断面)通常出现在钻头的中心处或者边缘处;切削断面B(宽切削断面)在钻头布齿密度较低的内锥上能观察到;而切削断面C在钻头布齿密度较高的外锥上(鼻部、肩部和外径弧面)能观察到。

图1 PDC齿在井底的典型切削断面Fig.1 Typical downhole rock cutting shapes
1.1 岩石的强度准则及失效分析
岩石材料的真实应力-应变特性十分复杂,包含非线性、弹塑性、黏弹性、剪胀性以及各向异性等特性。为此,选用能较好模拟岩石材料的线性Drucker-Prager塑性模型来进行模拟计算,该模型能模拟压缩屈服强度远大于拉伸屈服强度的材料,并假设偏应力和平均应力为线性关系,其屈服准则的表达式为
σq-σptanφ-f=0
(1)
σq=σ0-σ3
(2)
(3)
式中,σp为材料平均应力;σq为von Mises等效应力;φ为材料的内摩擦角;f为材料的黏聚力;σ0为材料的屈服应力;σ3为材料所受到的围压。

(4)
式中,ks为与材料性能有关的参数;τmax为最大剪应力。
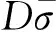

图2 渐进损伤过程的应力-应变曲线Fig.2 Stress-strain curve during failure process
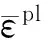
根据上述岩石模型,采用有限元软件ABAQUS进行三轴压缩模拟,选用的南充砂岩物理参数如表1所示[11-12]。图3所示为岩石的三轴压缩有限元模型,其中岩石高为101 mm,直径为49.6 mm,采用六面体8节点减缩积分单元(C3D8R)对岩石材料进行离散,划分网格为9 792个单元。对岩石上下端进行轴向位移约束,在岩石上端施加轴向压缩位移2.5 mm,在岩石的侧面施加的围压p分别为0、10 MPa、30 MPa及60 MPa,图4所示为岩石的应力-应变曲线。由图4可知,在实验条件下,随着轴向应变的增大,其岩石经过弹性变形、塑性变形及应变软化三个阶段,应力随着应变的增大而逐渐增大,当应力达到岩石的抗压强度时,岩石发生破坏,随后应力突然下降。而随着围压的增大,岩石的抗压强度逐渐增大,表明岩石的破碎难度增大。数值模拟结果与实验结果基本吻合,说明采用该模型能够较好地模拟岩石的破坏,这也证明了岩石模型的可靠性。
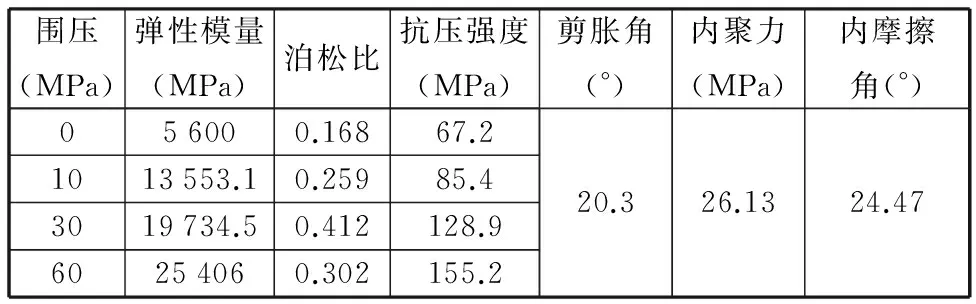
表1 岩石的物理参数Tab.1 The physical parameters of rock
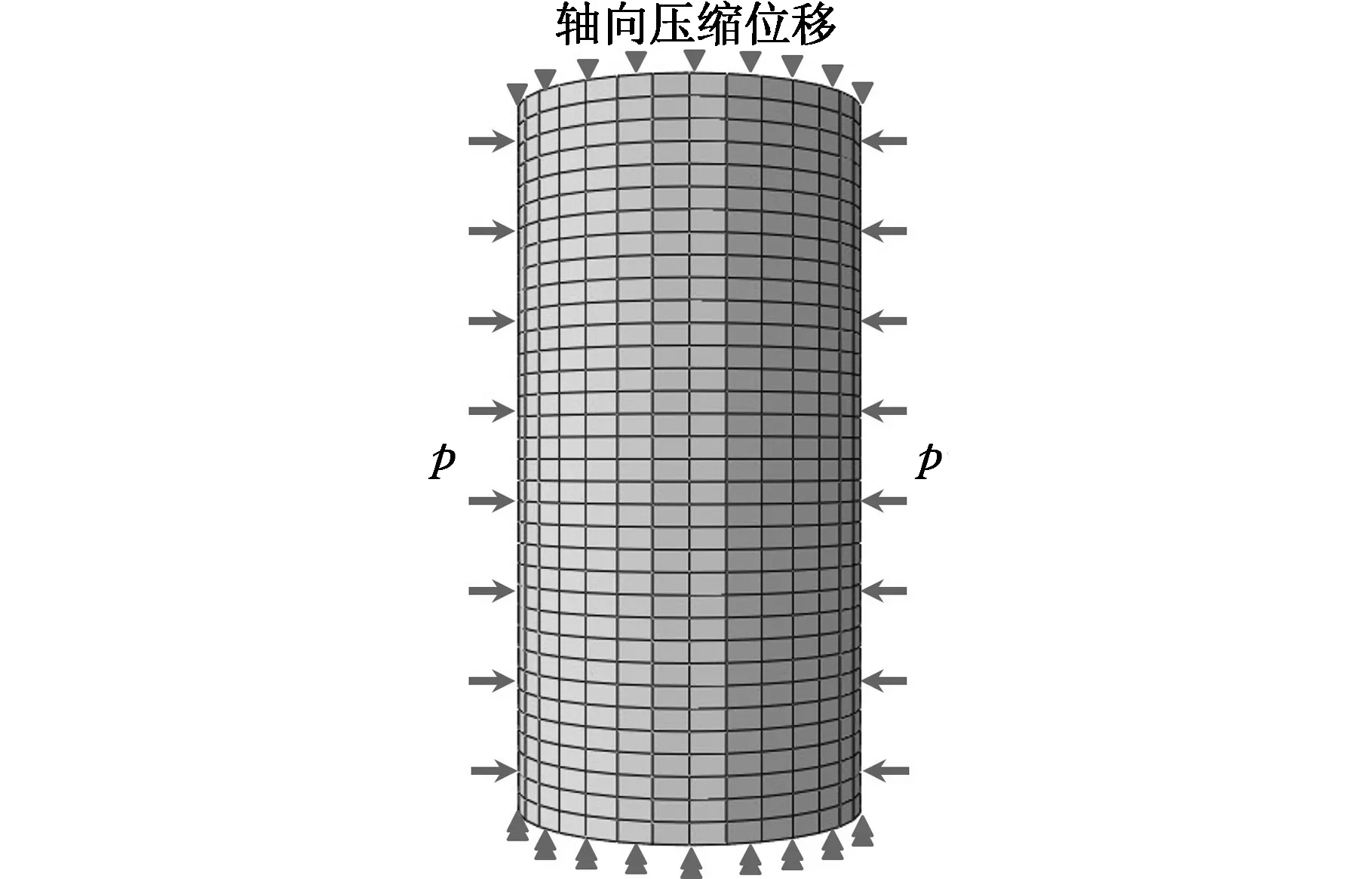
图3 岩石的三轴压缩有限元模型Fig.3 Triaxial test finite element model (FEM)
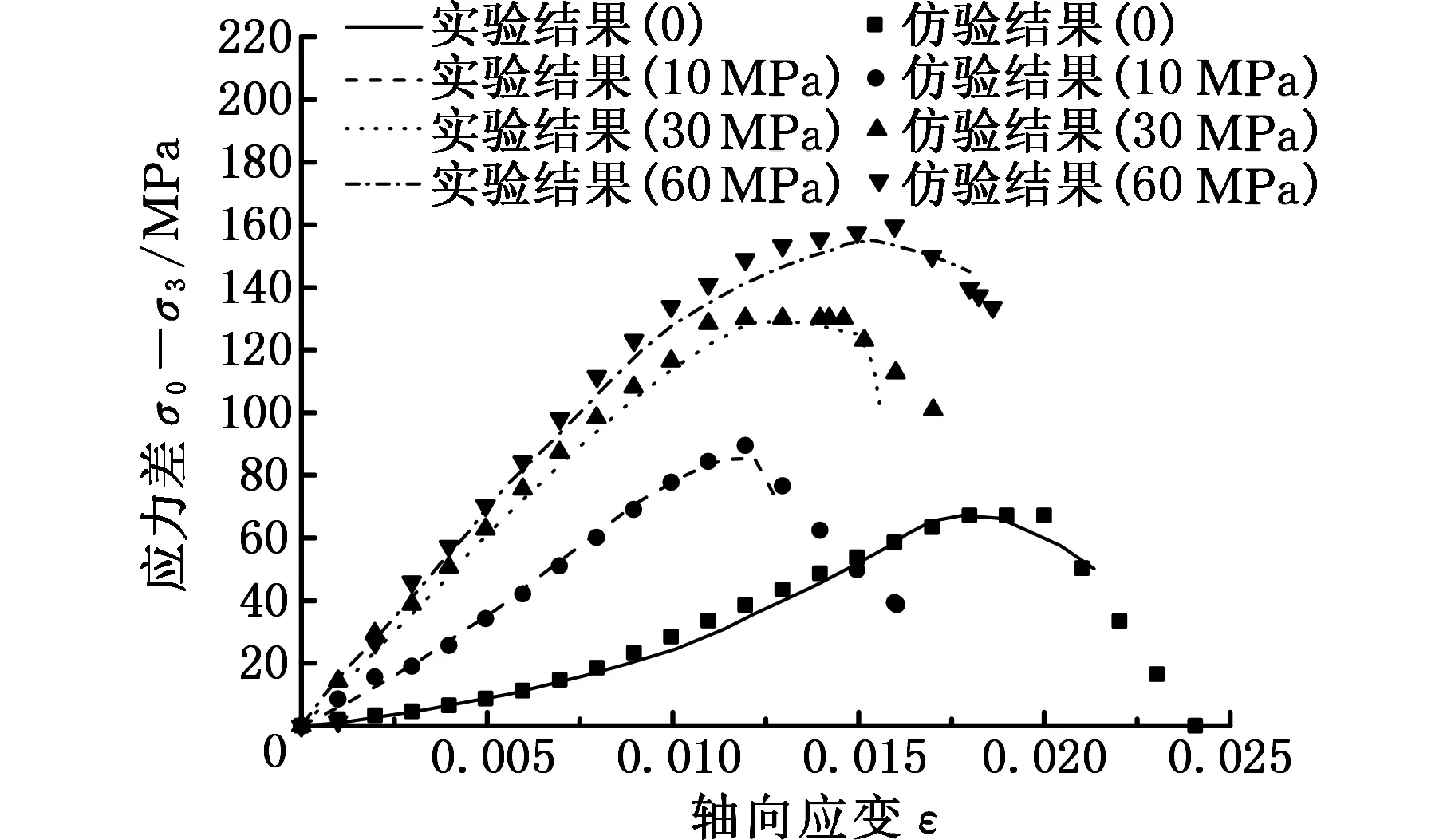
图4 岩石的应力-应变曲线Fig.4 Stress-strain curve of rock
1.2 PDC切削齿与岩石相互作用模型
为便于计算与分析,对切削齿与岩石相互作用进行基本假设:切削齿的强度和硬度远高于岩石的强度和硬度,因此将切削齿假设为刚体,忽略钻进过程中的切削齿磨损,当岩石单元失效后即从岩石中删除,忽略其失效后对后续切削的影响。
在切削齿破岩过程中,PDC齿的切向力为Fc,切削投影面积为A,α为切削齿的后倾角,β为切削齿的侧转角,其中O点为切削齿面中心,如图5所示。
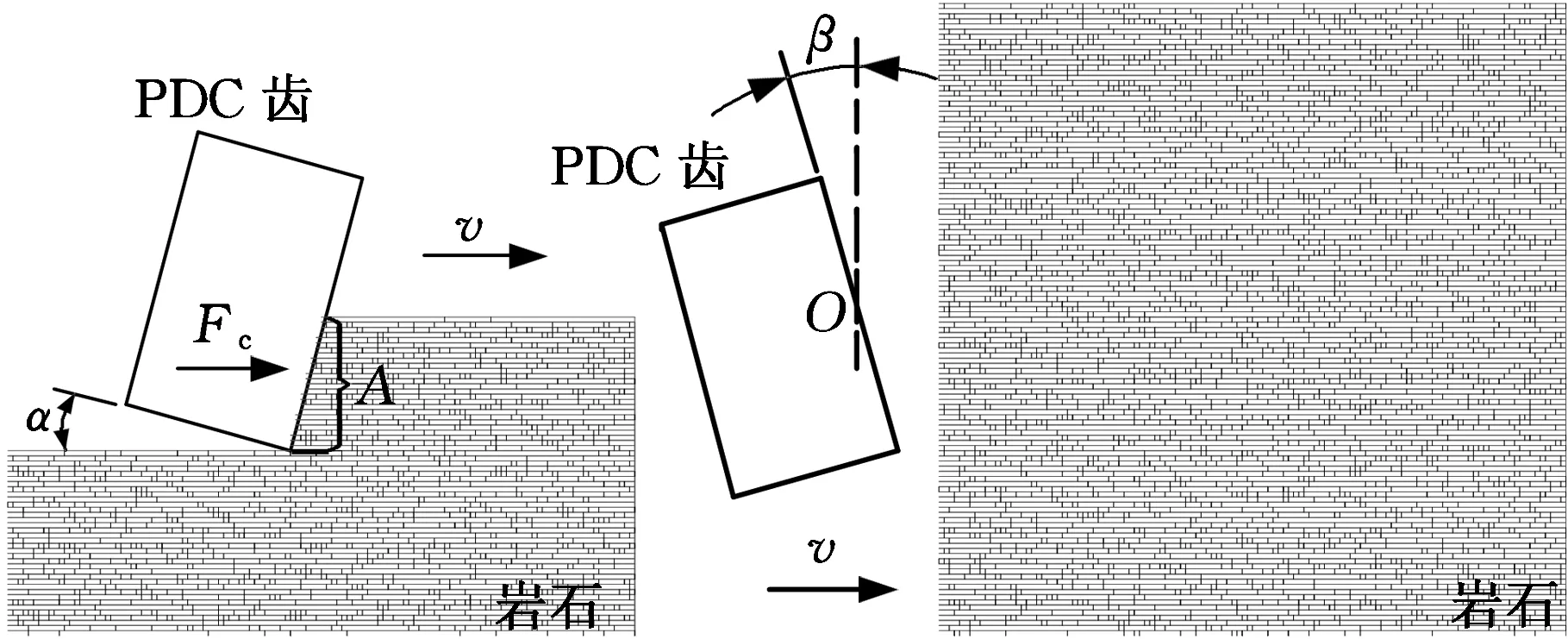
图5 PDC切削齿与岩石相互作用模型Fig.5 PDC cutter-rock interaction model
切削齿破碎岩石过程的非线性主要表现为:①短时间内结构的大位移与大转动所引起的几何非线性;②岩石单元因发生大应变直至破坏失效表现的材料非线性;③切削齿与岩石单元变形、失效和移除时产生接触动态变化所引起的接触非线性。采用有限元法设接触系统在时刻t占据空间域为Ω,作用在接触系统内的体积力、边界(虚位移及虚应变)及柯西内应力分别为Fv、qu、qε和σ,则接触问题归结为[13]
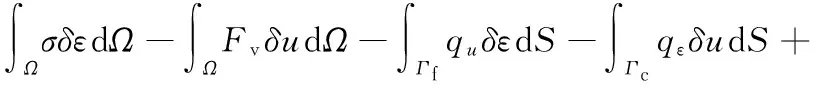
(5)
式中,Γf为给定边界力的边界;Γc为接触边界;S为接触区域;δu为虚位移;δε为虚应变;ρ为密度;a为加速度。
将空间域Ω用有限单元离散化并引入虚位移场,得到
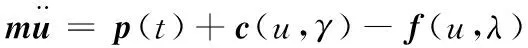
(6)

1.3 有限元模型的建立与验证
通过有限元软件ABAQUS建立三维实体仿真模型,其中PDC齿直径为13.44 mm,齿厚为8 mm,岩石在X、Y、Z方向的尺寸分别为50 mm、60 mm和20 mm,定义齿的切削深度为2 mm,后倾角为15°,侧倾角为0°。在有限元模型中,岩石体和切削齿均采用六面体8节点减缩单元(C3D8R),且将被切削部分岩石体进行网格细化,无断面岩石的网格数为479 700,PDC齿的网格数为11 072,岩石与PDC齿之间采用节点与面的接触属性,并设定接触面的摩擦因数为0.25。约束岩石底面的所有自由度,其余面不施加约束,给定PDC齿X方向的切削速度为1.2 m/s,仿真时长为0.03 s,PDC齿切削无断面南充砂岩的有限元模型如图6所示。数值分析得到的切削力随时间变化的曲线如图7所示,切削力平均值为299.39 N,最大值为703.28 N,而文献[12]实验中切削齿切削无断面南充砂岩的平均切削力为279.59 N,最大值为677.38 N。虽然数值结果与实验结果有一定的误差,但误差在合理的范围内,表明了切削齿切削岩石建模方法的可行性。
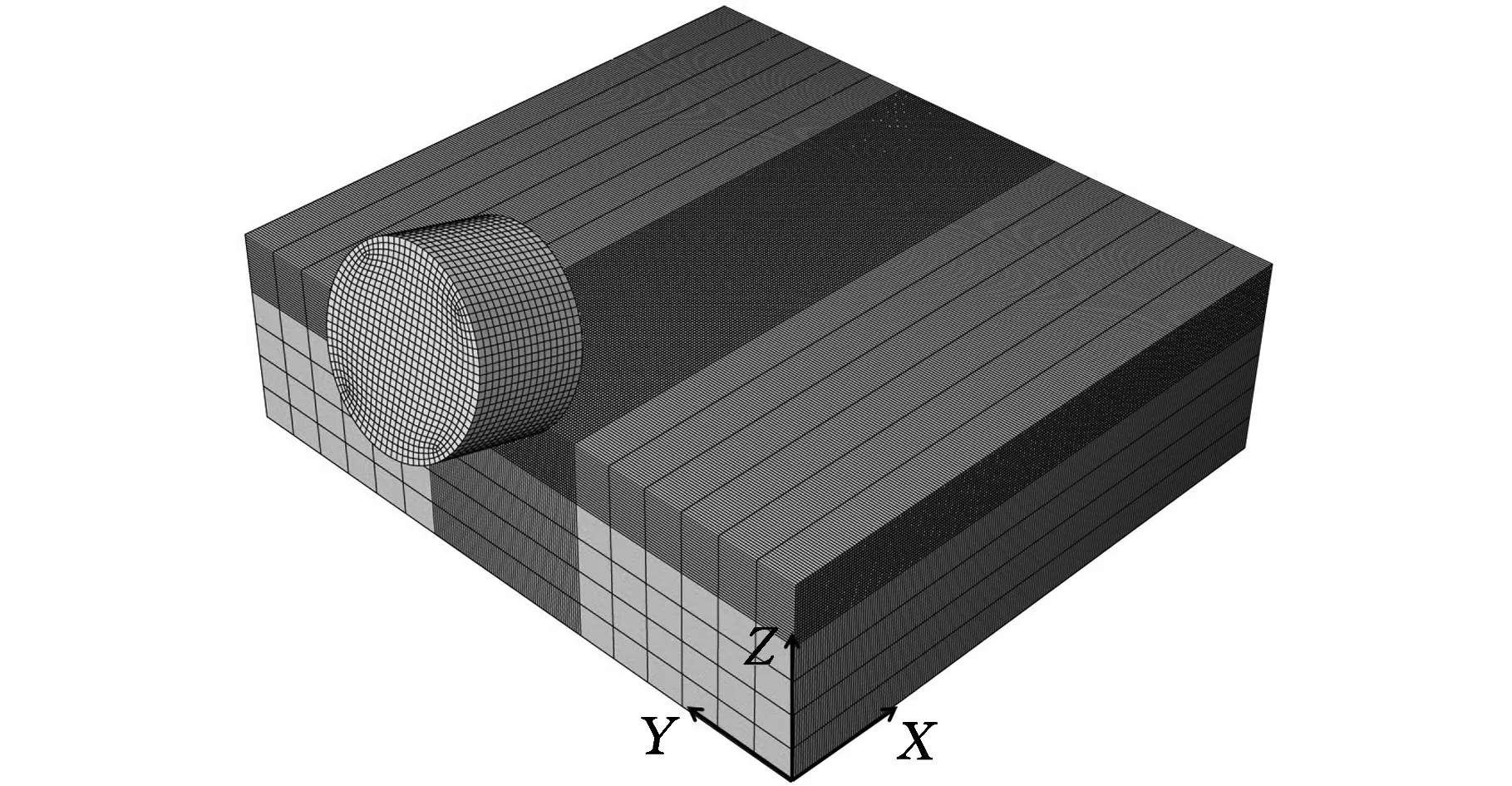
图6 PDC齿切削无断面岩石的有限元模型Fig.6 PDC cutter-rock FEM without cutting shapes
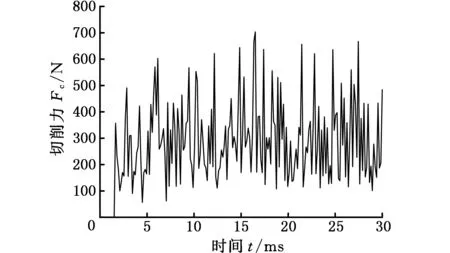
图7 切削力随时间变化的曲线Fig.7 Variations of tangential forces with time
基于上述PDC齿破岩的建模方法及岩石的本构模型,对切削齿切削断面岩石进行有限元建模,其中岩石切削断面A、B、C的网格数分别为475 200,630 000和667 800。约束岩石底面的所有自由度,对岩石的侧面施加围压,切削齿与岩石的相互作用区域施加静水压力,未作用区域的岩石上端面施加上覆岩层压力,其余参数保持不变,PDC齿切削断面岩石的有限元模型如图8所示。

图8 PDC齿切削断面岩石的有限元模型Fig.8 PDC cutter-rock FEM with cutting shapes
2 结果分析与讨论
2.1 破岩效率的评价方法
基于钻井参数、钻头类型和岩石参数来预测钻井效率的模型有很多,但使用最多的是机械比能,其定义为刀具切削单位体积所消耗的能量[14],即
(7)
式中,EMS为机械比能;W为破碎岩石消耗的功;V为破碎岩石的体积。
对于单个PDC齿切削岩石而言,式(7)中的功W等于平均切削力Fc乘以切削距离d,同时破碎体积V等于投影面积A乘以切削距离d,见图5。因此,式(7)可以改写为[15]
(8)
2.2 切削断面的面积对岩石机械比能的影响
图9所示为不同围压下,切削齿(后倾角为20°,侧转角为0°)切削3种切削断面的机械比能与切削面积的关系曲线。从图9a和图9b中可以看出,随着切削面积的增大,切削断面A和B的机械比能逐渐增大,而切削断面C的机械比能先增大后减小,对比3种切削断面和机械比能可以发现,切削断面C的机械比能最大,不利于岩石的破碎。从图9c和图9d中可以看出,随着切削面积的增大,切削断面A和B的机械比能都逐渐增大,而切削断面C的机械比能先增大后减小;在图9c中,当切削面积小于22 mm2时,切削断面C的机械比能最大,当切削面积大于22 mm2后,切削断面B的机械比能最大;而在图9d中,当切削面积小于15 mm2时,切削断面C的机械比能最大,当切削面积大于15 mm2时,切削断面A的机械比能最大。
由图9分析结果可知,在同一围压下,受切削面积的影响,不同切削断面的PDC齿破岩效率相差较大,使得PDC钻头存在切削齿破岩效率不匹配的问题。在低围压下(围压为0和10 MPa),由于切削断面B的破岩效率优于切削断面C的破岩效率,且减小切削面积有利于岩石的破碎,此时应增大PDC钻头内锥的井底覆盖面积以增加切削断面B的布齿,并降低切削齿的切削面积;随着围压的增大,在低切削面积下切削断面对岩石破碎效率的影响降低,且破岩效率最高,此时建议钻头上的切削齿都应采用小的切削面积。
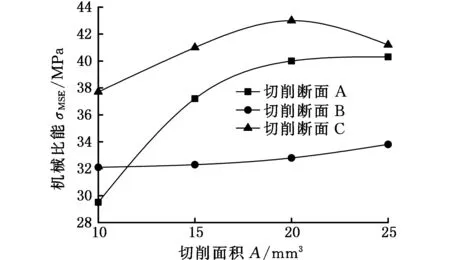
(a) 围压为0
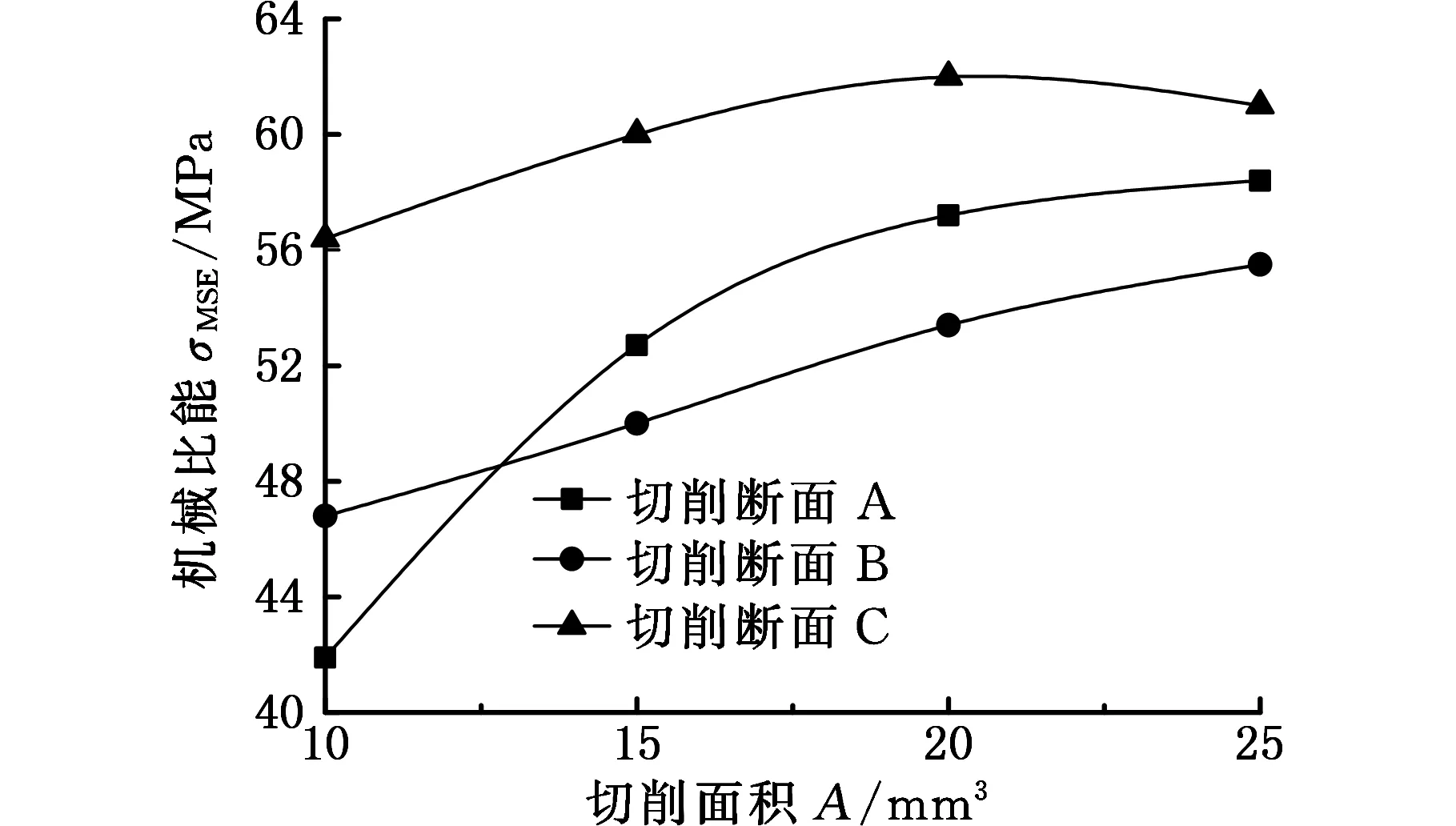
(b) 围压为10 MPa
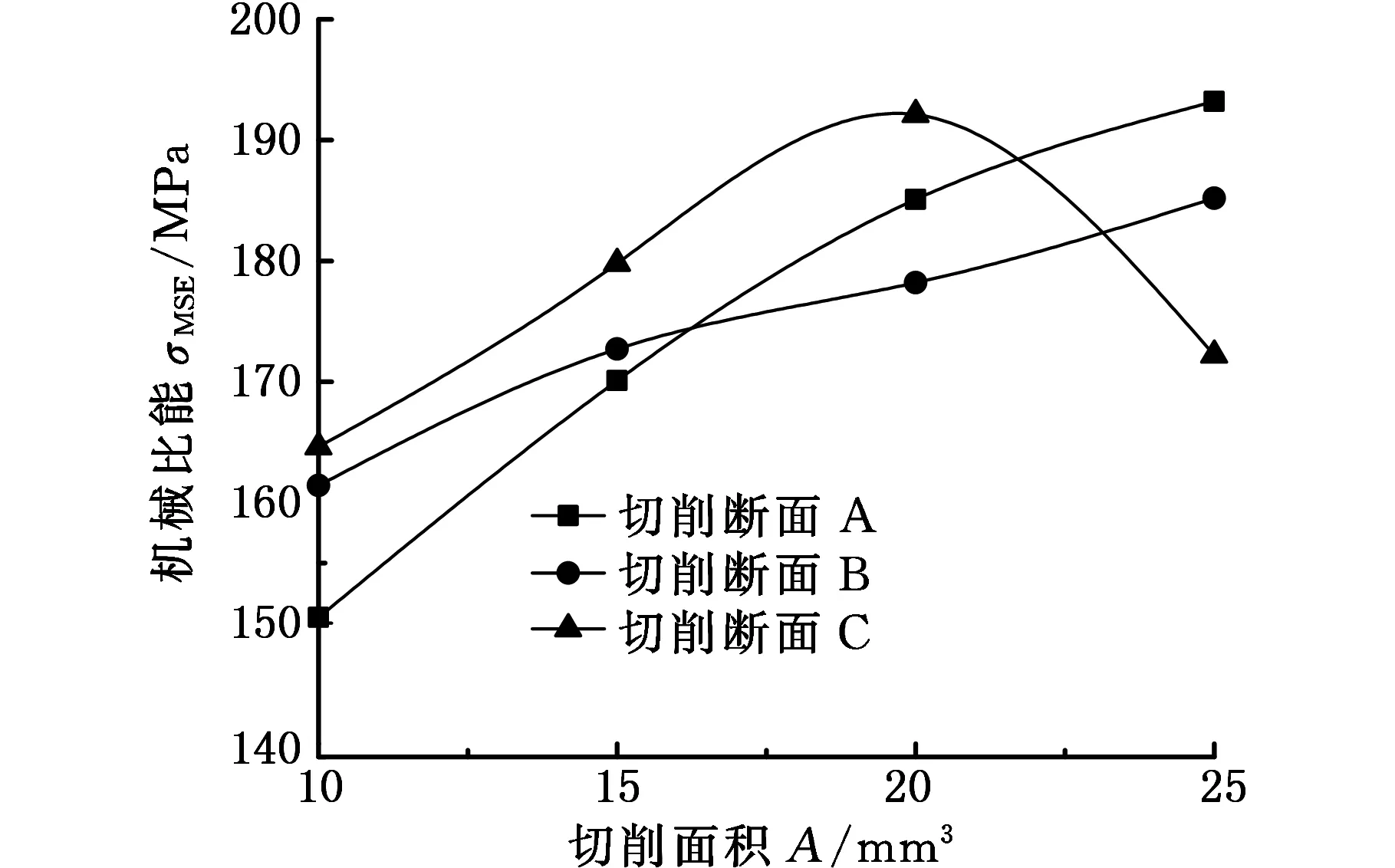
(c) 围压为30 MPa
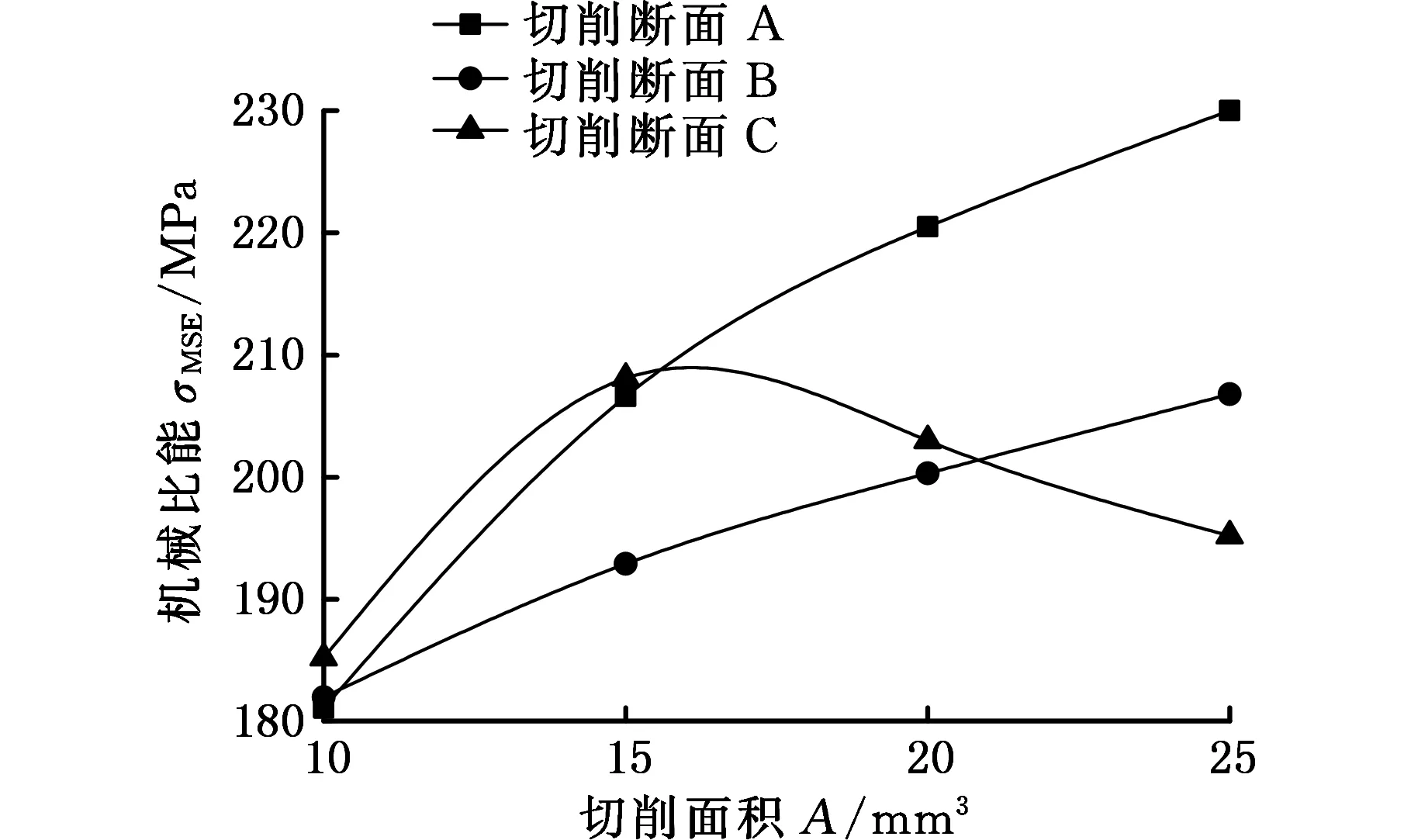
(d) 围压为60 MPa图9 切削面积对机械比能的影响Fig.9 Effect of cutting area on MSE
2.3 切削齿后倾角对岩石机械比能的影响
图10所示为不同围压下,切削齿(侧转角为0°,切削面积为20 mm2)切削3种切削断面的机械比能与后倾角的关系曲线。从图10a和图10b
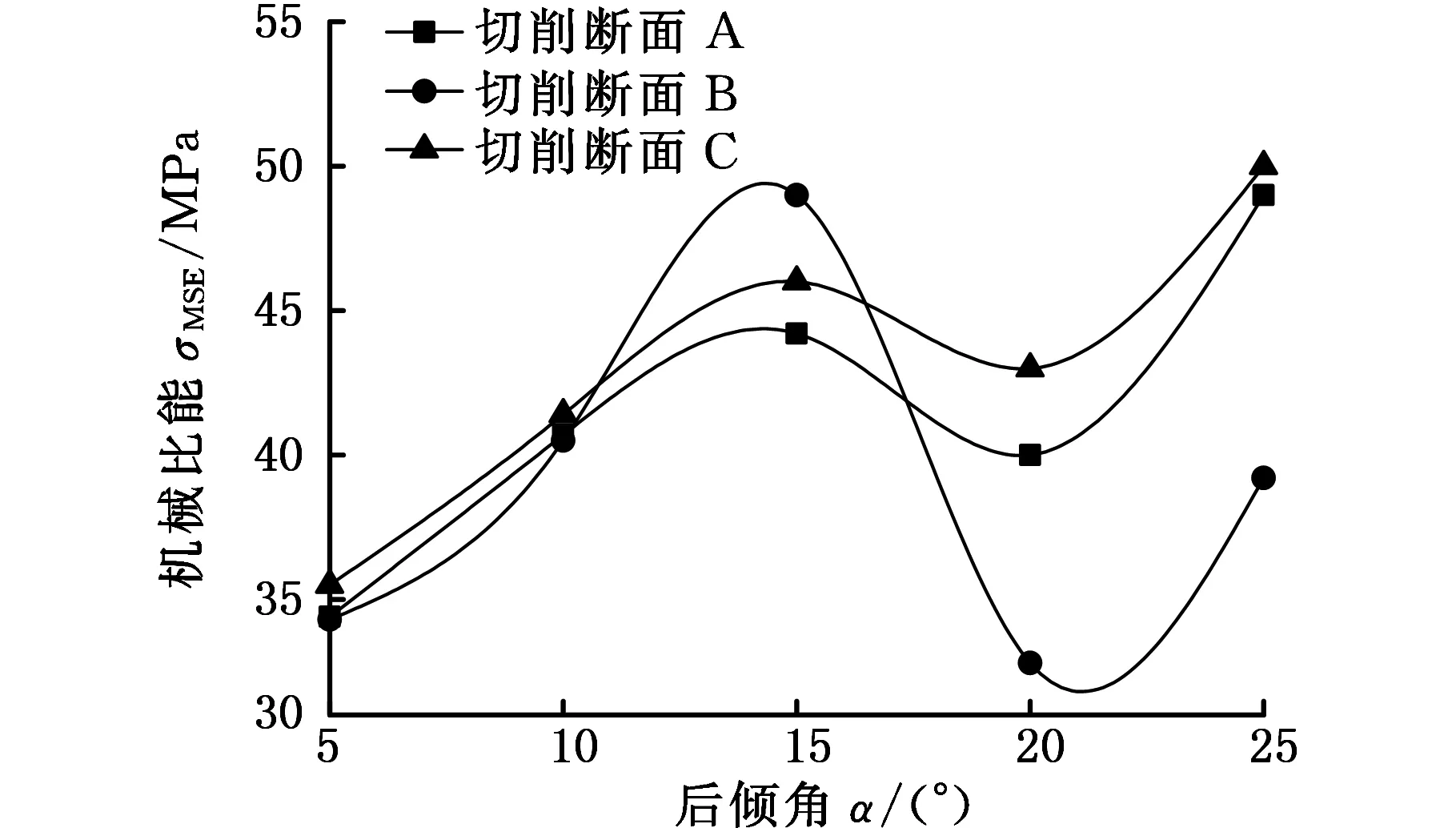
(a) 围压为0

(b) 围压为10 MPa

(c) 围压为30 MPa
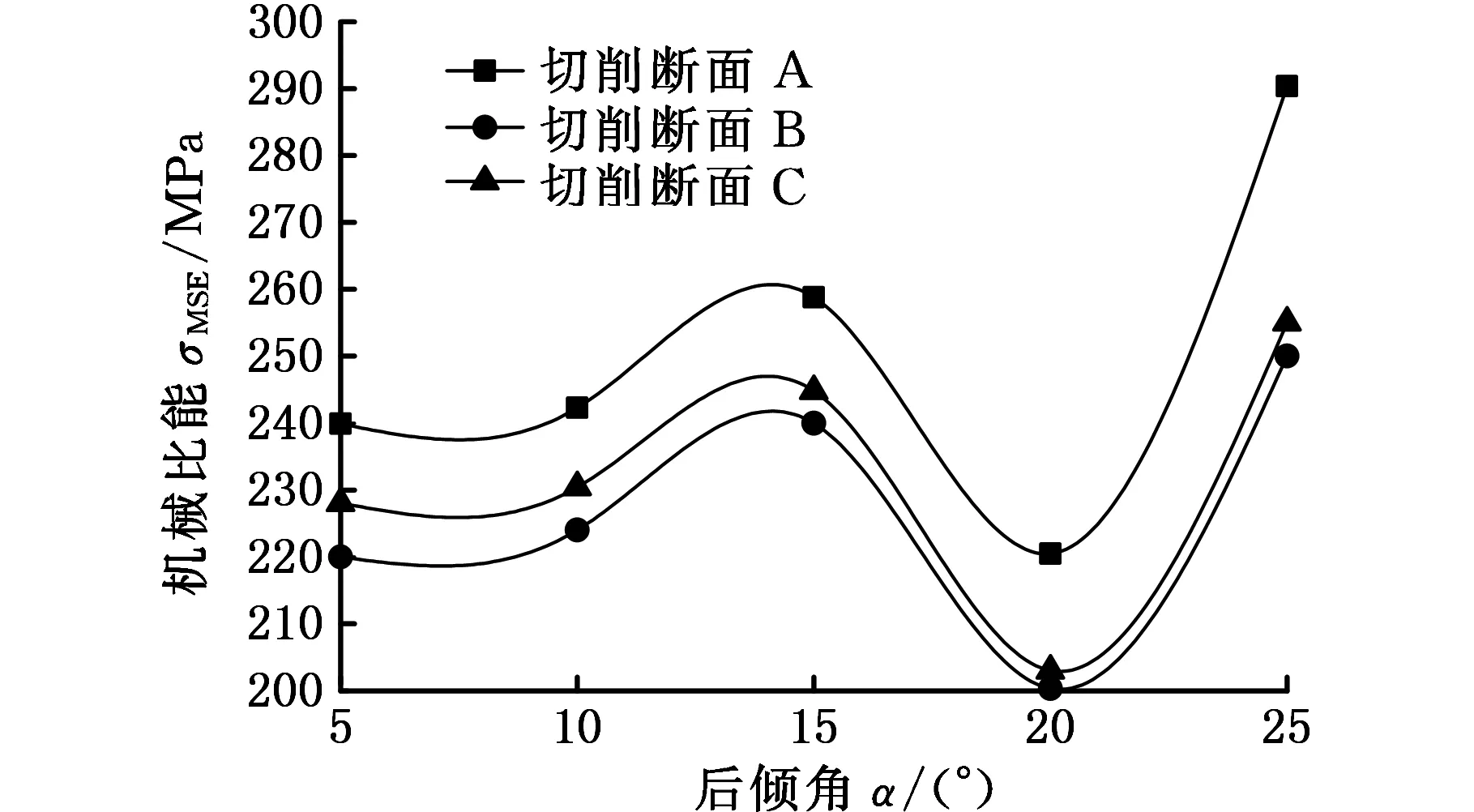
(d) 围压为60 MPa图10 后倾角对机械比能的影响Fig.10 Effect of back rake angle on MSE
中可以看出,随着后倾角的增大,切削断面A和C的机械比能整体呈现增大的趋势,其中后倾角为5°时的机械比能最小,而切削断面B的机械比能先增大后减小再增大,其最优破岩后倾角为5°或20°。从图10c和图10d中可以看出,随着后倾角的增大,切削断面A、B、C的机械比能都表现为先增大后减小再增大,其中图10c的最优破岩后倾角都为5°或20°;而图10d的最优破岩后倾角都为20°。
由图10分析结果可知,低围压钻进所用PDC钻头,切削断面A和B的最优破岩后倾角为5°,而切削断面C受后倾角的影响较大,建议采用5°或20°的后倾角;随着围压的增大,3种切削断面受后倾角的影响相同,此时,建议采用的后倾角都为20°。
2.4 切削齿侧转角对岩石机械比能的影响
图11所示为不同围压下,切削齿(后倾角为5°,切削面积为20 mm2)切削3种切削断面的机械比能与侧转角的关系曲线。从图11a中可以看出,随着侧转角的增大,切削断面A、B、C的机械比能都表现为先增大后减小,其中在侧转角为15°时的机械比能最大,不利于岩石的破碎;由图11b~图11d可知,随着侧转角的增大,切削断面A、B、C的机械比能都逐渐增大,其中破岩效率的最优侧转角为0°。由图11还可以知道,无论是低围压还是高围压,小角度侧转角是有利于岩石的破碎的,而且对比图10可知,在相同围压下,切削齿的机械比能受侧转角变化的影响小于后倾角对机械比能的影响,这是因为侧转角主要作用是对已破碎岩石产生推力,从而实现钻头排屑,而后倾角是影响破岩效率的主要因素。因此,对于切削齿在PDC钻头上布齿角度的选取,主要考虑切削齿的后倾角,且建议在满足钻头排屑的基础上选用小角度侧转角。
3 结论
(1)基于弹塑性力学和岩石力学,以 Drucker-Prager 准则作为岩石的屈服准则,剪切准则作为岩石的失效准则,将岩石三轴压缩数值模拟的应力-应变曲线与实验结果进行对比,验证了所用岩石模型的正确性,并对比分析了单齿切削无断面岩石数值结果与实验结果,验证了齿破岩建模方法的可行性。
(2)受切削面积的影响,在低围压下,切削断面对切削齿破岩效率的影响较大,其中切削断面C的破岩效率最低,此时应减少该布齿方式;随着围压的增大,低切削面积下切削断面对岩石破碎效率的影响降低,且破岩效率最高。

(a) 围压为0

(b) 围压为10 MPa

(c) 围压为30 MPa
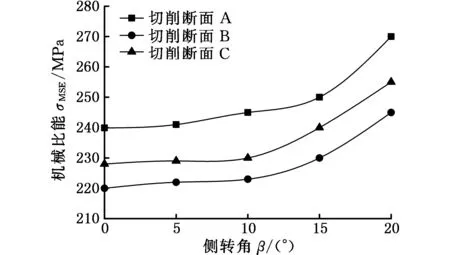
(d) 围压为60 MPa图11 侧转角对机械比能的影响Fig.11 Effect of side rake angle on MSE
(3)在低围压下,切削断面A和B在PDC齿后倾角为5°时的破岩效率最高,而切削断面C的最优破岩后倾角为5°或20°;随着围压的增大,3种切削断面的机械比能都随着后倾角的增大表现为先增大后减小再增大,其中最优破岩后倾角都为20°。
(4)在相同围压下,随着侧转角的增大,切削断面A、B、C的机械比能都呈现增大的趋势,但整体影响不如后倾角,在进行PDC钻头上布齿角度的选取时,主要考虑切削齿后倾角的影响,且建议在满足钻头排屑的基础上采用小角度侧转角。
参考文献:
[1] ATICI U, ERSOY A. Correlation of Specific Energy of Cutting Saws and Drilling Bits with Rock Brittleness and Destruction Energy[J]. Journal of Materials Processing Technology,2009,209(5):2602-2612.
[2] HIBBS L E, FLOM D G. Diamond Compact Cutter Studies for Geothermal Bit Design[J]. Journal of Pressure Vessel Technology,1978,100(4):406-416.
[3] 梁尔国, 李子丰, 邹德永. PDC钻头综合受力模型的试验研究[J]. 岩土力学,2009,30(4):938-942.
LIANG Erguo, LI Zifeng, ZOU Deyong. Experimental Research on Integrated Mechanical Model of PDC Bit[J]. Rock and Soil Mechanics,2009,30(4):938-942.
[4] RAJABOV V, MISKA S Z, MORTIMER L, et al. The Effects of Back Rake and Side Rake Angles on Mechanical Specific Energy of Single PDC Cutters with Selected Rocks at Varying Depth of Cuts and Confining Pressures[C]//IADC/SPE Drilling Conference and Exhibition. San Diego: Society of Petroleum Engineers, SPE-151406-MS, 2012:1-17.
[5] HARELAND G, NYGAARD R, YAN W, et al. Cutting Efficiency of a Single PDC Cutter on Hard Rock[J]. Journal of Canadian Petroleum Technology,2009,48(6):60-65.
[6] MARTINEZ I R, FONTOURA S, INOUE N, et al. Simulation of Single Cutter Experiments in Evaporites through Finite Element Method[C]//SPE/IADC Drilling Conference. Amsterdam:Society of Petroleum Engineers,SPE-163504-MS,2013:1-14.
[7] CARRAPATOSO C, DA FONTOURA S A B, Martinez I M R, et al. Simulation of Single Cutter Experiments in Evaporite Using the Discrete Element Method[C]//ISRM International Symposium-EUROCK. Wroclaw:International Society for Rock Mechanics,2013:223-232.
[8] CARRAPATOSO C, DA FONTOURA S A B, INOUE N, et al. New Developments for Single-cutter Modeling of Evaporites Using Discrete Element Method[C]//ISRM Conference on Rock Mechanics for Natural Resources and Infrastructure-SBMR. Goiania:International Society for Rock Mechanics,2014:1-8.
[9] 祝效华,李海. PDC切削齿破岩效率数值模拟研究[J]. 应用基础与工程科学学报,2015,23(1):182-191.
ZHU Xiaohua, LI Hai. Numerical Simulation on Mechanical Special Energy of PDC Cutter Rock-cutting[J]. Journal of Basic Science and Engineering,2015,23(1):182-191.
[10] CHEN S, GROSZ G, ANDERLE S, et al. The Role of Rock-chip Removals and Cutting-area Shapes in Polycrystalline-diamond-compact-bit Design Optimization[J]. SPE Drilling & Completion,2016,30(4):334-347.
[11] 余长柏. PDC钻头切削齿破岩有限元仿真研究[D]. 成都: 西南石油大学,2009.
YU Changbai. The Simulation Analysis of Rock-breaking Process with the Cutters of PDC Bit[D]. Chengdu: Southwest Petroleum University,2009.
[12] 邓敏凯. PDC钻头切削齿破岩效果优选研究[D]. 成都: 西南石油大学,2011.
DENG Minkai. Optimization Research on the Effect of PDC Cutters Fracturing Rock[D], Chengdu: Southwest Petroleum University,2011.
[13] 王清峰, 朱才朝, 宋朝省, 等. 牙轮钻头单牙轮的破岩仿真研究[J]. 振动与冲击,2010,29(10):108-112.
WANG Qingfeng, ZHU Caichao, SONG Chaosheng, et al. Non-limear Dynamic Analysis of a Roller Cone Bit-well Rock System with Rock-cone Bit Interaction[J]. Journal of Vibration and Shock,2010,29(10):108-112.
[14] TEALE R. The Concept of Specific Energy in Rock Drilling[J]. International Journal of Rock Mechanics and Mining Science,1965,2(1):57-73.
[15] ZHOU Y, ZHANG W, GAMWO I K, et al. Mechanical Specific Energy Versus Depth of Cut[C]//46th US Rock Mechanics/Geomechanics Symposium. Chicago:American Rock Mechanics Association, ARMA-2012-622,2012:1-6.
