一道2016年北京大学生命科学冬令营数学试题的研究

广东省佛山市乐从中学(528315) 林国红

本文分析了2016年北京大学生命科学冬令营数学试题的第13题,给出几种解法,同时进一步探究了此问题.特意成文,与读者分享.

一、试题

设直角梯形的高为2,其两条对角线交点为P,以它的两底中点的连线为直径的圆与此梯形的直腰相交于点E和F,则P到E和F这两点的距离之和为( )

二、解法呈现

解法一如图1,在直角梯形ABCD中,设边AD,BC的中点为M,N,易得AC,BD,MN交于点P.J,H分别为LN,LM 的中点,由,得PO=KO,即∠OEP=∠ONK,延长EP,EO分别交圆于G,Q,有 EG=LN=AB,且 ∠POG= ∠EOL= ∠FOP,故 △FOP = △GOP,所以EP+PF=EG=AB=2.故选B.

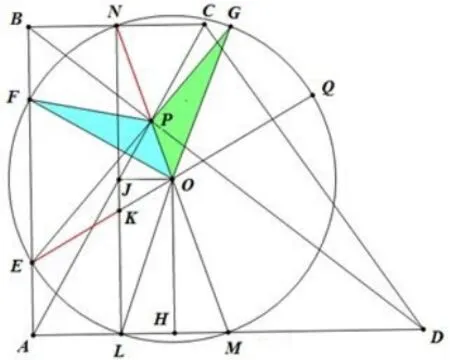
图1

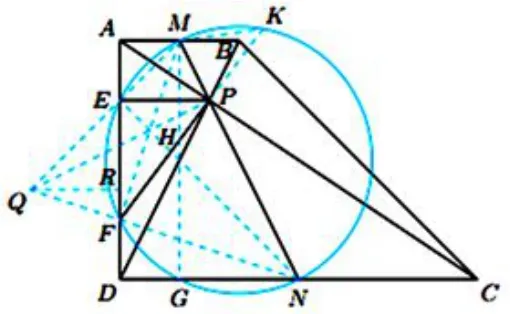
图2

解法二如图2,在直角梯形ABCD中,AB//CD,∠BAD= ∠ADC=90°.AD=2,AB=2a,CD=2b.M,N分别为线段AB,CD的中点,对角线AC与BD交于点P.以MN为直径的圆与线段AD交于E,F两点,与线段CD交于N,G两点,连接MG.延长FP,交圆于点K,连接MK.设直线ME与NF交于点Q,直线MF与NE交于点H,作QR⊥AD于R.易知,M,P,N三点共线.由,所以直线MF,NE,QP交于一点H,而H是△QMN的垂心,故 ∠EFM= ∠ENM= ∠PFH,因而弧 ME=弧MK,从而有PE=PK.因为弧FK=弧ME+弧MK+弧EF=弧ME+弧EF+弧FG=弧MG,所以PE+PF=PK+PF=FK=MG=AD=2,故选B.

图3

解法三如图3,AB//CD,∠BAD= ∠ADC=90°,AD=2.M,N 分别为线段AB,CD的中点,对角线AC与BD交于点P.以MN为直径的圆与线段AD交于E,F两点,与线段CD交于N,G两点,连接MG.延长FP,交圆于点K,连接MK.连接ME与NF.因为又因为 ∠MEP+ ∠NEP=90°,∠MEA+ ∠NED=90°,所以 ∠MEP= ∠MEA,∠NEP= ∠NED.同理,得∠NFP= ∠NFD,∠MFP= ∠MFA,故弧 ME= 弧MK,从而有ME=MK,PE=PK.又因为弧KF=弧MG,所以PE+PF=PK+PF=FK=MG=AD=2,故选B.

三、探究引伸

通过进一步的探究,发现此题与椭圆的性质有关.

引理1如图4(1),椭圆两顶点为A,B,椭圆上任一点P(A,B除外)的切线与过A,B且垂直于AB的两直线交于D,C,则

图4(1)

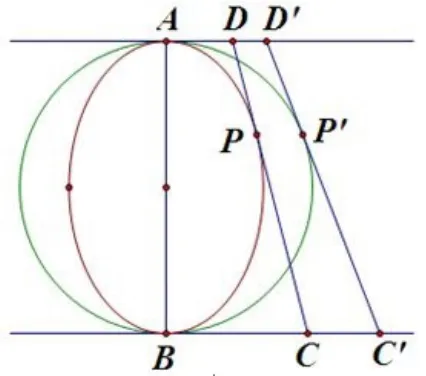
图4(2)

引理1简证作伸缩变换将椭圆还原为圆,如图4(2),还原后由于切线长相等,显然有,而变换前后两边的比值不变,故还原前等式也成立.

利用同一法可证“引理1”的逆命题,即如下命题成立.

命题1直角梯形ABCD,AB为直腰,P为CD上一点,且满足,则以A,B为顶点且过P的椭圆与CD切于P.

引理2如图4(3),P为椭圆上不是长轴顶点上任一点,过点P的切线与过长轴顶点与长轴垂直的直线相交于S,T,则以线段ST为直径的圆过这个椭圆的两个焦点.

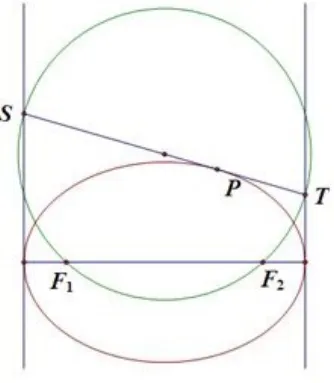
图4(3)

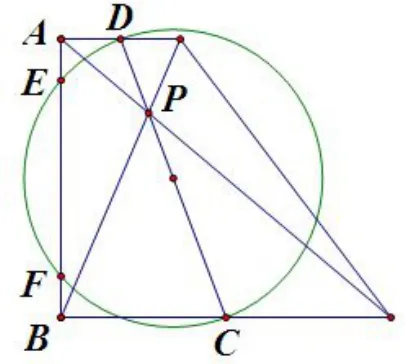
图4(4)

引理2证明如图4(3),设椭圆方程为,椭圆上除长轴外一点P(x,y),则有00即.因为切线ST的方程为所以由,可得由,可得.故,所以有

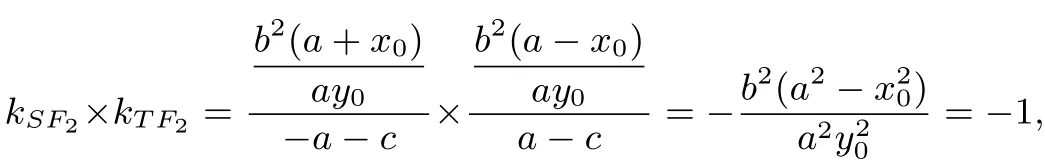
即∠SF2T=90°.同理可得∠SF1T=90°,所以命题得证.

回到原题,如图4(4).设以A,B为顶点且过P的椭圆为Γ,由C,D是中点,易知,故由命题1知Γ与CD切于P,再由引理2可知E,F是Γ的两个焦点,从而有PE+PF=AB=2,故选B.