探究一道竞赛题 破解一类函数题

浙江省宁波市第四中学(315016) 蒋亚军 魏定波

1 试题呈现

若关于x的方程x2+ax+b−3=0(a,b∈R)在[1,2]上有实根,则a2+(b−4)2的最小值为___.

本题为2017年福建省高中数学竞赛试卷第8题,从题面上看,考查的是以“函数和方程”为载体,不等式为主线的典型问题,着重考查学生分析问题、解决问题的能力,能够检验学生对二次方程与二次函数之间关系的认知程度,对转化思想、分类讨论思想、数形结合思想的掌握情况.

2 解法探究

解法1依题意可得

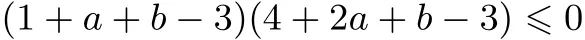
或

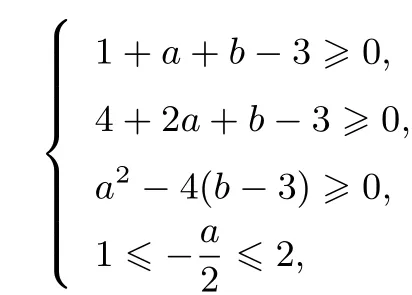
作出满足条件的点(a,b)区域(如图1所示),于是,得a2+(b−4)2的最小值等于点(0,4)到直线a+b−2=0的距离平方,即为2.

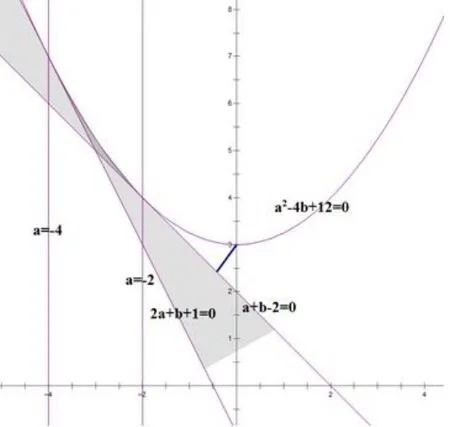
图1

解法2设f(x)=(x−α)(x−β)且α∈[1,2],于是有a= −(α+β),b−3= αβ.所以

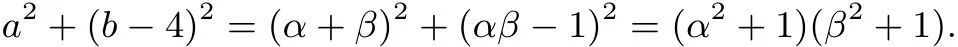
因为α∈[1,2],β2≥0,所以a2+(b−4)2≥α2+1≥2,当且仅当α=1,β=0,即a=−1,b=0时,a2+(b−4)2取得最小值2.

解法3 由x2+ax+b−3=0,得b=−x2−ax+3,所以

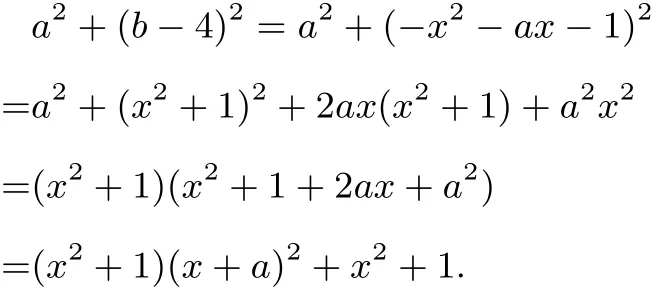
因为x∈[1,2],(x+a)2≥0,所以a2+(b−4)2≥x2+1≥2,当且仅当x=1,a=−1,b=0时,a2+(b−4)2取得最小值2.

解法4若以a,b为主元,“若关于x的方程x2+ax+b−3=0(a,b∈R)在[1,2]上有实根,求a2+(b−4)2的最小值.”转化为:求点(0,4)到直线l:xa+b−3+x2=0上的点(a,b)的最小值问题,显然,点到直线的距离最小.

当x∈[1,2],

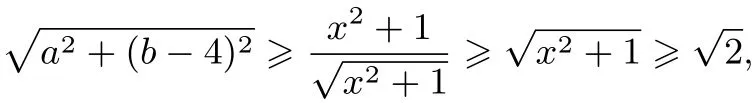
所以a2+(b−4)2取得最小值2.

评注由于学生在处理二次函数零点问题时普遍有思维定势,能得到相应的不等式组,据此借助线性规划的原理,运用数形结合的思想方法是不错的选择,它能避免一些复杂的不等式转换,需要将不等式(组)等价转化为相对准确的图形.解法3虽然过程简捷,但变换技巧较强.解法4需要转换一下思路,以待定的x为参数,以a,b为主变量,构造出新的函数(或方程),用“零点式”求解,它不仅可以回避一些复杂的图形,而且能避免多变量不等式组的繁琐讨论,从提升学生的思维品质出发,相比之下有必要对解法2的方法进行挖掘与普及.

3 方法运用

例1(2017年浙江省高考数学模拟试卷第17题)已知函数f(x)=x2+ax+b(a,b∈R).在区间(0,1)内有两个零点,则3a+b的取值范围是____.

解析设f(x)=(x−α)(x−β)且α,β∈(0,1),于是有a= −(α+β),b= αβ.所以3a+b= −3(α+β)+αβ =(3−α)(3−β)−9,由于 α,β ∈(0,1),则2＜ 3−α ＜ 3,2＜3−β＜3,所以3a+b∈(−5,0).

例2(2015年浙江省高考数学(文)科第20题)已知函数f(x)=x2+ax+b(a,b∈R)在[−1,1]上存在零点,0≤b−2a≤1,求b的取值范围.

解析设s,t为方程f(x)=0的解,且−1≤t≤1,则s+t=−a,st=b.由于0≤b−2a≤1,因此

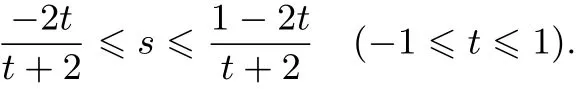
当0≤t≤1时,

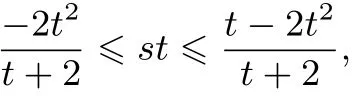
由于

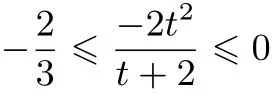
和

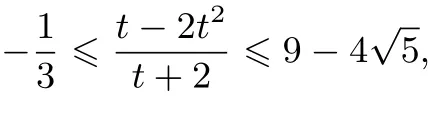
当−1≤t＜0时,

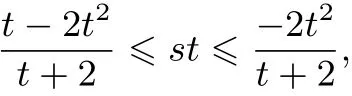
例3(2007年全国高中数学联赛辽宁赛区初赛试题)若关于x的方程有实根,则a2+b2的最小值为___.

解析方法(1)设,由于,将问题转化为:若a,b是可使方程f(u)=0在(−∞,−2]∪[2,+∞)上至少有一个实根,求a2+b2的最小值.

设 f(u)=(u−α)(u−β)且|α|≥ 2,所以 a2+b2=(α+β)2+(αβ)2=(β2+1)α2+2αβ+β2,当β＞0时,由于,所以

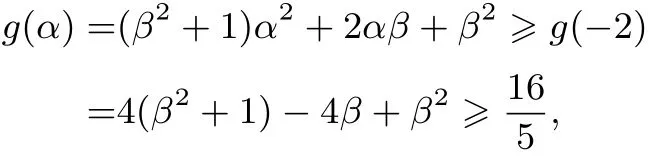
方法(2)因为u2≥4,所以

故a2+b2的最小值为

例4(2014年杭州市第一次统测数学试题(理科))设

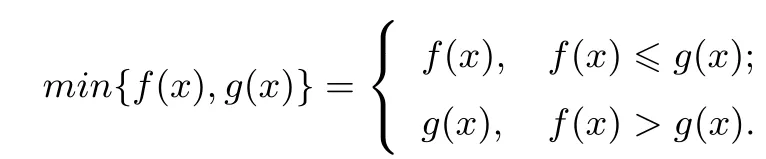
若函数f(x)=x2+px+q的图象经过两点(α,0),(β,0),且存在整数n,使得n＜α＜β＜n+1成立,则是( )

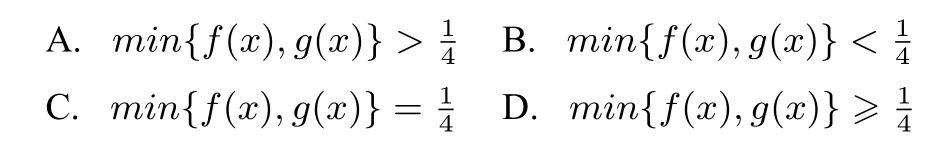
解析设

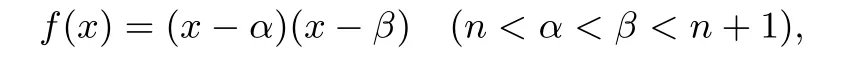
依题意,得f(n)＞0,f(n+1)＞0,所以

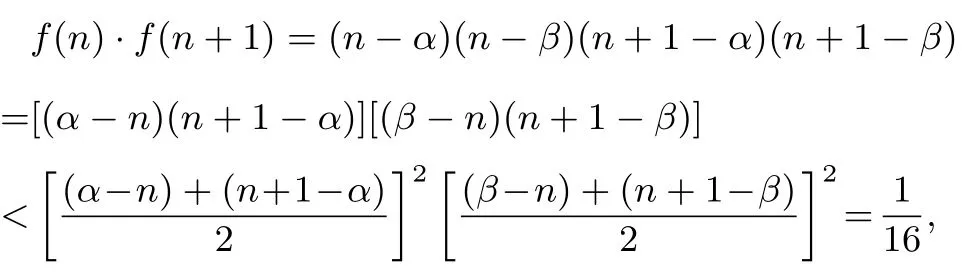
4 几点感悟

4.1 总结常考题型,提升数学思想方法

综观高考与模考函数零点的试题,题型新颖别致、自然流畅,内容综合,解法灵活.函数零点问题将函数、方程、不等式很好地“揉”在一起,具有一定的综合性和灵活性,计算或画图也比较复杂,需要有较强的综合能力,并蕴含着函数与方程思想、分类讨论思想、数形结合、转化与化归等数学思想,在复习中教师可以以专题的形式给学生在这些数学思想方法上进行渗透.

4.2 重视一题多解,提升学生思维品质

对于一些典型问题,通过一题多解,帮助学生从多个切入口,较广泛地联系不同的数学知识和思想方法,同时培养学生解题后反思的习惯.让学生学会一题多解,有利于培养学生的发散思维能力和解题技巧;有利于学生提高解决综合问题的能力;有利于创新意识的形成和发展,是提高学生数学核心素养的一个有效途径.

4.3 立足通性通法,着眼学生思维发展

在我们平时的教学实践中,已经看到通性通法在数学解题中的重要作用.这种具有普遍意义的解题方法,在解决问题中是最适用的,是数学方法的主流,也是高考中的重要考查点.由于教学的核心是以学生发展为主旨,我们重新挖掘了这道竞赛题的教学价值,同样是解题通法,选择哪种方法好,要看问题的结构和学生的认知水平,也要避免太过于执着通法通解,而引起的思维僵化.