运用平面向量构造解题的“二化”思想

广东省广州大学附属中学(510050) 韩智明

平面向量作为代数和几何的纽带,素有“与几何联姻,与代数牵手,与解析几何交汇”之美称,正是由于其兼具“数”“形”的双重身份,加之解法灵活多样,变化多端,备受高考命题者的青睐.近年来,以平面向量作为载体出现的试题形式新颖,内涵丰富,突显数学能力,确实让很多考生头痛不已.在充分考查学生学科核心素养的今天,运用平面向量知识构造解题恰好具备了数学抽象、逻辑推理、数学建模、直观想象等特点,从历年高考真题和各地市模拟题中,我们也不难看到这方面知识频频考查的踪影.笔者在整理近几年高考真题和模拟题时发现,考生要熟练掌握运用平面向量知识构造解题,必须理解学会以下两种解题思想,即“二化”思想.坐标化思想:是指解决向量求值、最值或范围问题时,把有关已知条件和所求结论,在直角坐标系中恰当地表示出来,这样就将向量运算完全代数化,可使很多几何问题转化为学生熟悉的有关有明确关系的数量运算,从而降低问题的难度,是处理向量求值、最值或范围问题常用的方法,坐标化思想体现了化归与转化的思想,函数与方程的数学思想.图形化思想:是指解决向量求值、最值或范围问题时,把已知条件和所求结论在图形中表示出来(往往结合其几何意义),借助图形思考、解决问题,图形化思想体现了化归和转化、数形结合的数学思想.

下面就几个例题与大家一同探讨:

例1已知实数x,y满足x2+(y−2)2=1,则的取值范围是( )

分析本题初看很难入手,所求如果通过代入坐标几乎不可能,用其它方法处理显得计算量很大,只能通过转化将其化为所学熟知的数学知识处理,不难想到平面向量相关知识来通过构造数学模型处理.

图1

解析设,则

评注此题运用平面向量的坐标化思想把转化为两个向量的夹角的余弦问题,再利用图形化思想来处理,显得简洁直观.

例2(2011年高考全国卷理科第12题)设向量a,b,c满足,则 |c|的最大值等于( )

分析本题题干简洁,朴实无华,但真正做起来似乎又让人无从下手,仔细品味条件a·b=−1,说明a,b的夹角为120°,而 〈a − c,b − c〉=60°,让我们想到四点共圆,从而打开了解题思路,使问题解决,快速地得到解答.

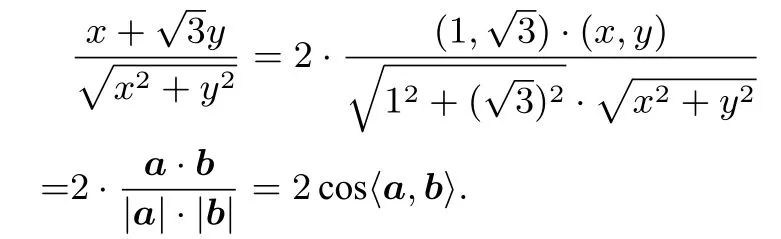
解析如图2,设,,则,,由,得,即 ∠AOB=120°.又因为,即∠ACB=60°,所以O,A,C,B 四点共圆.

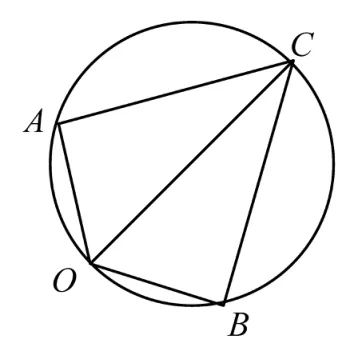
图2

当OC为圆的直径且O、C在AB的异侧时,|c|取得最大值,此时 ∠OAC= ∠OBC=90°,∠ACO= ∠BCO=30°,则,即|OC|=2|OA|=2,故选A.

评注本解法利用图形化的思想方法,各种数量关系在图形中非常明了,本题是数形结合思想在平面向量中的典型应用,从解题过程中我们领略了图形化策略思想解决数学问题的独特魅力.

例3已知平面向量a,b满足|a|=|b|=2,存在单位向量e,使得(a−e)·(b−e)=0,则|a−b|的取值范围是____.

分析1 利用已知条件求出向量a·b+1=(a+b)·e,两边取模,再由|(a+b)·e|≤|a+b|,再两边平方,求得a·b的范围,再求|a−b|的平方范围,即可得到所求范围.

解析1因为(a−e)·(b−e)=0,所以a·b+1=(a+b)·e,两边取模可得 |a·b+1|=|(a+b)·e|,而 |(a+b)·e|≤ |a+b|,即有|a·b+1|≤|a+b|,两边平方得:(a·b+1)2≤(a+b)2即为(a·b)2≤ a2+b2−1=4+4−1=7,即则|a−b|2=a2+b2−2a·b,即.故答案为:

分析2 通过平面向量的几何意义,如图在平面直角坐标系中分别设出a,b,a−e,b−e对应的向量,然后运用平面向量的图形化思想转化(a−e)·(b−e)=0的几何意义即为要,即∠AMB=90°,即为以AB的直径的圆和单位圆有交点即可.

图3

解析2如图3,设点A和点B是圆x2+y2=4上任意两点,且向量a,b对应的向量分别是,则.点M 是单位圆上任意一点,则向量对应的向量为单位向量e,则向量a−e或b−e对应的向量是或,要使得 (a − e)·(b − e)=0,只要,即∠AMB=90°,即为以AB的直径的圆和单位圆有交点即可.设|AB|=2R,则在△OAN中,由勾股定理可得:|OA|2=|ON|2+|AN|2,即 22=R2+(R+1)2,即2R2+2R−3=0解得,当∠AOB 增大时,|AB|的长度也变大,直到在另一面与单位圆相切,此时

评注解析1注重代数运算,但|(a+b)·e|≤|a+b|的思路建立要求较高;解析2对学生理解平面向量的几何意义要求很高,此解法能力立意高,对学生运用平面向量的图形化思想处理数学问题得到很好的训练,突显思路清晰直观.

例4已知向量α,β,γ且满足|α|=1,|α−β|=|β|,(α− γ)·(β−γ)=0,若对每一确定的β,|γ|的最大值和最小值分别是m,n,则对任意β,m−n的最小值为___.

分析此题变量较多,学生对主、次变量的选择有困难,在理解题意方面要求较高,更多地想到运用坐标化思想处理问题;然而通过对|α|=1,|α−β|=|β|,(α−γ)·(β−γ)=0几何意义的理解,运用图形化思想转化处理会使题意更加体现数学魅力.

解析1把α放入平面直角坐标系,使α起点与坐标原点重合,方向与x轴正方向一致,则α=(1,0),设β=(x1,y1),因为 |α − β|=|β|,所以,所以.设γ=(x,y),则α−γ=(1−x,−y),.因为 (α−γ)·(β −γ)=0,所以,化简得,,即

最小值

解析2因为|α|=1,所以令,则A必在单位圆上,又因为向量 β 满足 |α − β|=|β|,令,则点B必在线段OA的中垂线上,.又 因 为(α−γ)·(β−γ)=0,故 C点在以线段 AB为直径的圆M 上,任取一点C,记.故m−n就是圆M的直径|AB|,显然,当点B在线段OA的中点时,(m−n)取最小值.即,故答案为

评注解析1注重坐标化思想,解法具有一般的通性,但是过程显得繁冗,计算量较大,注重“数”的运算;解析2运用图形化思想将题意进行化归,解法新颖别致,深刻展示平面向量的几何意义,解法技巧灵活,要求较高,注重“形”的转化.

例5(2015年高考浙江卷理科第15题)已知向量e1,e2是空间单位向量,,若空间向量b满足,且对于任意x,y∈R,|b−(xe1+ye2)|≥|b−(x0e1+y0e2)|=1(x0,y0∈R),则x0=____,y0=____,|b|=____.

分析本题对向量的考查要求较高,是一道体现向量知识的综合好题,可以利用两边平方,求出|b−(xe1+ye2)|取到最小值时x0、y0的值及|b|;可以运用坐标化思想来处理,但是和例3相似要求考生对题中主、次元进行选择然后配方;也可以运用图形化思想结合向量的几何意义进行转化.

解析1对于任意x,y∈R,|b−(xe1+ye2)|≥|b−(x0e1+y0e2)|=1(x0,y0∈R)说明当x=x0,y=y0时,|b−(xe1+ye2)|取得最小值1.

（四）母猪产前保健 在母猪妊娠85 d至分娩前5～7 d，用中药饲喂母猪，预防母猪产前疾病带入产仔过程中。主要针对蓝耳病、圆环病毒、伪狂犬、霉形体感染等经母仔传播或并发的病原提前预防，降低发病率，并且在妊娠后期做好抗应激工作，以防流产。在分娩前40 d做好有关疫苗的免疫工作。在母猪产前2周注射大肠杆菌疫苗，产前1周再注射一次，以起到减少初生仔猪黄白痢发生的作用。

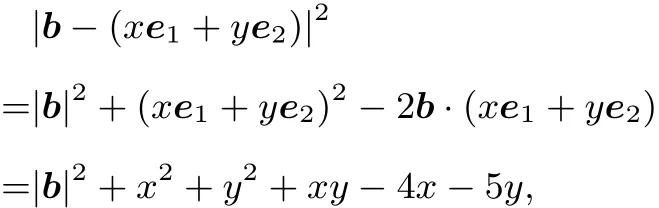
要使|b|2+x2+y2+xy−4x−5y取得最小值,需要把x2+y2+xy−4x−5y看成关于x的二次函数,即f(x)=x2+(y−4)x+y2−5y,其图象是开口向上的抛物线,对称轴方程为,所以当时,f(x)取得最小值,代入化简得,显然当y=2时,f(x)min=−7,此时.此时

解析2因为,所以.不妨设,b=(m,n,t).由题意知

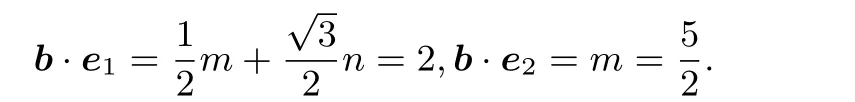
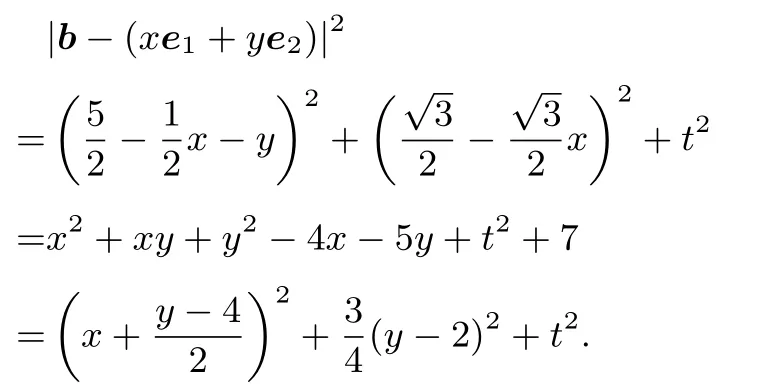
由题意知,当x=x0=1,y=y0=2时,取到最小值.此时t2=1,故|b|=

解析3假设b,e1,e2共起点O,则b−(xe1+ye2)的终点一定与b的终点相同(不妨设为B),而它起点则为向量xe1+ye2的终点(不妨设为O),由平面向量定理可知xe1+ye2的终点为e1,e2所确定的平面(不妨设为α)内的任意一点.又因为|b−(xe1+ye2)|≥|b−(x0e1+y0e2)|=1,显然当 BO⊥α 时满足条件.因为 b·e1=2,,结合三垂线定理(线面垂直)可知xe+ye在e,121e2上的投影同为2和.因为,所以,,即有x0=1,y0=2,此时由勾股定理得

评注解析1是纯代数法,解析2运用坐标法思想处理,两种解法开始过程不同,但后面的步骤和思路一样,都要分主、次元看作某一变量的二次函数进行配方求出最值,但这样的处理要求考生有一定的技巧且有较大的计算能力;解析3是运用图形化思想处理,结合向量的几何意义分别把和|b−(xe1+ye2)|≥|b−(x0e1+y0e2)|=1用图形的形式进行建模转化,解法充分展示向量的图形化特征,技巧性强,精彩灵活.

例6(2013年高考数学浙江卷理科第15题)设e1,e2为单位向量,非零向量b=xe1+ye2,x,y∈R,若e1,e2的夹角为的最大值等于____.

解析1因为e1,e2为单位向量,非零向量,因为e1,e2,b=xe1+ye2,x,y∈R,e1,e2的夹角为,得

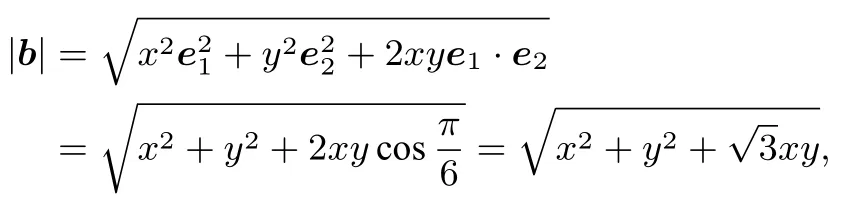
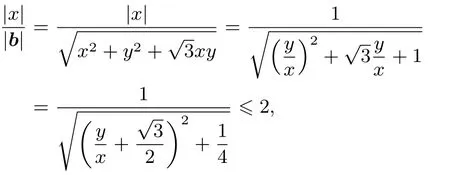
解析2把xe1看成一个固定向量,由一维定理或平行四边形法则可知b=xe1+λe2(λ=y)(在共起点O之后b的终点一定在过xe1终点A且平行于ye2的直线AB上),那么比值显然在b与直线AB垂直时达到最大,即

解析3因为x,y∈R,且y与解题无关,所以b=xe1+ye2可以改写成b=xe1−λe2.那么由三角形法则可知b的终点在A点处,则其起点就一定在直线OC上,那么显然当CA⊥OC时的比值达到最大,.

评注解析1通过代数法将所求二元问题转化为一元问题的二次函数求其最值,计算要求较高.解析2和解析3都是先通过技巧处理然后从不同角度通过图形化思想进行转化,由平面向量的几何意义得出转化后的结果,转化巧妙,构思新颖别致,活用了平面向量的“形”的特征.

例7(2016年高考四川卷理科数学第10题)在平面内,定点A,B,C,D 满足|,,动点P,M 满足,则的最大值是( )

分析根据,可知点A,B,C在以D 为圆心,为半径的圆上.由,易得 ∠ADC= ∠ADB= ∠BDC=120°,.因为动点P,M 满足,所以点P在以点A为圆心,1为半径的圆上,M是PC的中点,综合题干信息然后根据题意进行合理转化.距离的平方的,所以

图4

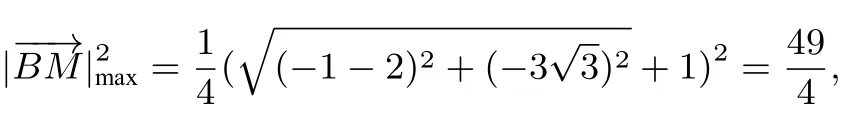
故选B.

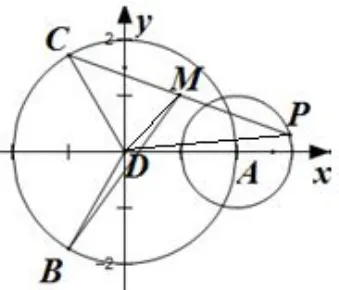
图5

解析2如图5,连接DM,DP, 则 有,

解析3如图6,顺次连接A,B,C三点,构成△ABC.根据可知,△ABC为等边三角形,点D为等边△ABC的中心且BD=2.设AC中点为N,连接AP,则NM为 △APC的中位线,即 NM=.因此PC的中点M在以点N为圆心,(为半径的圆上运动.显然取得最大值.故选B.

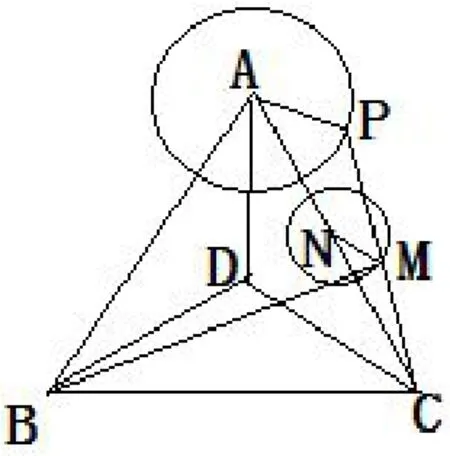
图6

解析1如图4,以D为原点,直线DA为x轴建立直角坐标系,则设P(x,y),由已知,得(x−2)2+y2=1.又,所 以,即.因此

它表示圆(x−2)2+y2=1上的点(x,y)与点

评注解法1利用坐标化思想,转化为两点距离求得最值;解法2利用向量的线性合成,转化为数量积求得最值;解法3利用图形化思想,求得点M轨迹,再通过挖掘问题的几何特征,求得最值,解答步骤更简捷.

向量是沟通代数、三角、几何等内容的桥梁之一,运用坐标化和图形化的“二化”思想处理和构造解决平面向量问题是体现数学学科核心素养的典型案例.而平面向量作为一种工具,它的特点在数学的许多方面都有体现,利用平面向量解决一些数学问题,将大大简化解题的步骤,使学生多掌握一种行之有效的数学工具.平面向量联系代数与几何,它可以使图形量化,使图形间关系代数化,使我们从复杂的图形分析中解脱出来,只需要研究这些图形间存在的向量关系,就可以得出精确的最终结论.平面向量知识很容易被处于高中文化水平之上的学生理解和接受,而且其所具有的良好的“数形结合”特点使它与中学数学知识能够融汇贯通,相辅相承.一旦学生掌握了平面向量相关知识,其学科核心素养也会得到良好的培养.很多数学问题在平面向量这一工具的参与下摆脱了纯几何推理,转换成简单的向量代数推理.