巧用“切线法”求解函数不等式

广东省佛山市罗定邦中学(528300) 龙宇

在不等式的相关问题中,“切线法”是一个基本方法.其思想本质是利用直线(即切线)将原来的复杂变量变为一次的式子.

一、“切线法”的基本运用

使用“切线法”的基本原则:对于涉及到的函数的图像要具有“凹凸性”.在函数的定义域内,函数的“凹凸性”要保持一致.

例1证明对数平均数与算术平均数间的关系:

分析该不等式的证明方法很多,这里应用“切线法”来证明:

证明如图1,构造函数,在区间[b,a]上积分等于曲边梯形BbaA的面积S,过A,B的中点点C处做的切线分别交Bb,Aa于点B1,A1.梯形B1baA1的面积根据中位线的性质,所以.由于“向下凸”,所以该切线完全在曲线的下方,所以S1＜S该不等式成立.

图1

例2(2012年全国新课标卷21题)已知函数f(x)满足.若求(a+1)b的最大值.

分析利用函数表达式的结构易得关于该问题的资料均利用分类讨论的方法求解,本文尝试一下 “切线法”:将不等式的两边视为两个独立的函数,令g(x)=ex,h(x)=(a+1)x+b.其中g(x)单调递增且“向下凸”,若要满足g(x)≥h(x).则有h(x)为g(x)的切线.

解设g(x)上的任意一点M(x0,ex0),过点M做g(x)的切线为:y=ex0x+(1−x0)ex0.对比函数h(x)可得:a +1=ex0,b=(1−x0)ex0.(a+1)b=e2x0(1−x0),令F((x)=e2x)(1−x),F′(x)=e[2x(1−)2x).显然可知F(x)在上单调递增,在上单调递减.所以F(x)在处取到最大值.所以(a+1)b的最大值为,对应的

二、创造“切线”

某些函数并不存在一次式,我们可以通过等价变形获得“切线”.

例3设函数f(x)=ex−1−x−ax2,若当x≥0时,f(x)≥0,求实数a的取值范围.

分析f(x)≥0⇔ex−1=ax2+x.显然当x=0时,该式恒成立.当x＞0时,原式.设新函数.构造原理:设函数h(x)=ax+1.易知函数h(x)恒过定点(0,1).通过一阶导可知F(x)单调递增,通过二阶求导可知F(x)的图像是“向下凸”的.为满足F(x)≥h(x),h(x)的斜率的极限状态为F(x)在x=0处的导数.

解求导可得:.因为(罗必塔法则).令G(x)=ex(x− 1)+1,求导可得:G′(x)=xex.可知G(x)在[0,+∞)上单调递增,且有G(x)≥ G(0)=0.所以,即F(x)在[0,+∞)上单调递增.所以当时,结论成立.

例3变式设函数f(x)=x(ex−1)−ax2,若当x≥0时f(x)≥0,求实数a的取值范围.

简要解答当x=0时,f(x)=0.当x＞0时,f(x)≥0⇔ ex−1≥ax.通过对不等式左边函数的分析,仿照例3可得a的取值范围(−∞,1].

例4设函数f(x)=x3−2x2−4x−7.设x0是函数y=f(x)的零点,实数α,β满足试探究实数α,β,x0的大小关系.

分析三个数中,β的值最难确定.但在β的表达式中出现了f(α)与f′(α).容易联想到y=f(x)在x=α处的切线:y=f′(α)(x− α)+f(α).显然β为该切线的横截距.本题的考察的内容依然是“切线法”.

解易得:函数f(x)在上单调递增,在上单调递减,在(2,+∞)上单调递增.且有.所以函数f(x)有唯一的零点x,利0用零点存在定理易知x0∈(3,4).根据题意f(α)＞0,可知α ＞ x0＞ 2,所以f′(α)＞ 0.

设函数在x=α处的切线为:y=f′(α)(x−α)+f(α).如果利用函数f(x)在(2,+∞)上的“凹凸性”可直接得结论α＞β＞x0＞ 2.因为f′′(x)=6x−4,当x∈(2,+∞)时,f′′(x)＞ 8,函数 f(x)在(2,+∞)上是 “向下凸”的.

回避“凹凸性”,利用该切线方程求解:分别将实数 α,β,x0代入切线方程:yx=α=f(α),yx=β=0,yx=x0=f′(α)(x0− α)+f(α) ＜ f(x0) ＜ 0. 最后一个表达式是因为该切线在函数f(x)的“下方”.设函数F(x)=f(x)−f′(α)(x−α)−f(α),求导可得:F′(x)=f′(x)−f′(α).当 x ∈ (2,α)时,F′(x)＜ 0,当 x ∈ (α,+∞)时,F′(x)＞ 0.所以F(x)在x=α处取到最小值,所以F(x)≥F(α)=0.所以上面的三个表达式成立.又因为该切线单调递增,所以α＞β＞x0.

后面的解答过程本质上还是利用了函数的“凹凸性”.该问题的实质提供了一个求三次方程近似解的方案.取α=4,过x=α做函数f(x)的切线,将该切线的横截距赋给α再代入上一步,反复操作,这里的横截距将会无限的接近函数f(x)的零点.即通过该流程可无限的逼近三次方程近似解.因为函数f(x)在(2,+∞)上是“向下凸”的,所以一开始令α=3也可获得答案.但如果取α=1,该流程则不一定能逼近该零点.

三、切线的升华:“支撑线”

“切线法”的本质在于切线位于函数的上方或下方,通过几何直观即可将原复杂的表达式化简.然而有些函数虽然具有“凹凸性”,但也不能用“切线”来求解.这时本文提出用“支撑线”来替代“切线”.

例5(2015年山东21题)设函数f(x)=ln(x+1)+a(x2−x).

(1)略;(2)若∀x＞0,f(x)≥0成立,求a的取值范围.

分析该题a的取值范围是[0,1].基本的解法是构造函数或分离参数.本文先尝试运用“切线法”.f(x)≥0⇔ln(x+1)≥−a(x2−x),且有x＞0,所以不等式的两边同除以x变形为.设函数

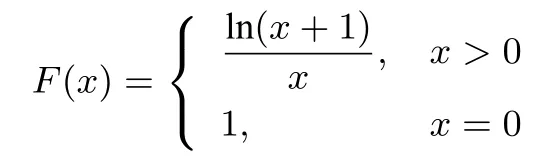
(其中x=0的值是通过极限求得的.)设G(x)=−a(x−1),直线G(x)过定点(1,0),斜率未知.对F(x)求导可得:

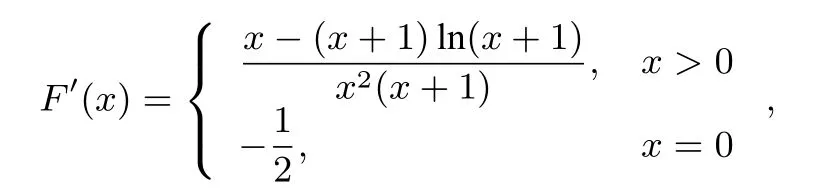
图2

解根据上面的分析,画出F(x)的图像,如图2.点B的坐标为(0,1).设F(x)在该点的切线为l.F(x)在该点的导数为,所以.因为F(x)在[0,+∞)上是“向下凸”的,所以F(x)在直线l的上方,证明过程可参考上面的例题.对于函数G(x),过定点A(1,0),为保证F(x)≥G(x),所以函数G(x)与F(x)至多只有一个交点B.

此时kAB=−1,因为,所以G(x)在[0,+∞)上位于直线l的下方,所以G(x)在F(x)的下方.即有F(x)≥G(x)是成立的.此时的a=1,显然可知当a∈[0,1]时,G(x)与F(x)至多只有一个交点B.而当a∈/[0,1],G(x)与F(x)的交点一定不是B.

反思本文旨在说明“切线法”或“支撑线”的运用原理及使用范围.所以解答过程相对复杂.若直接运用该技巧,特别在选择或填空题型中,该方法可极大的节省计算时间.