初始缺陷圆弧拱面内非线性失稳实验研究*

尹宸哲，禹奇才，刘爱荣，卢汉文，张骏峰

(广州大学—淡江大学工程结构灾害与控制联合研究中心，广东 广州 510006)

由于实际加工和制造的误差，任何具有确定几何形状的结构都不可避免地具有缺陷。承受轴向压力的拱也不例外，各种不同跨径和结构的拱均不同程度地存在着缺陷。拱结构只要存在初始几何缺陷，其稳定性就不再是平衡分支问题，而是极值点失稳问题。国内外学者对拱的静、动力稳定性进行了深入研究，但这些研究基本不考虑缺陷的影响[1-5]。个别学者利用有限元数值分析方法，通过引入整体一致的几何缺陷和事先假定的局部缺陷，研究了相关缺陷对拱的稳定性和极限承载能力的影响，例如：颜全胜等[6]针对考虑初始几何缺陷影响的梁单元，兼顾拱的面内初始变形的影响，把具有缺陷的拱当作具有缺陷的直压杆计算，并对钢管混凝土拱桥进行了非线性和稳定分析，结果表明缺陷对拱肋内力、应力和位移的影响系数均小于10%；程进等[7]编制了非线性程序，对考虑初始几何缺陷的大跨度钢管混凝土拱桥进行了稳定分析，验证了拱肋面外的初始缺陷对大跨度拱桥面内的极限承载力不会产生较大影响；谢旭等[8]采用弹塑性大变形计算方法，将几何缺陷分为单元局部缺陷和整体一致缺陷，发现几何缺陷使得大跨度拱桥的结构承载力降低了8%左右；戴云峰[9]提出了利用样条函数法分析理想拱的面内、面外稳定性，并建立了具有任意横向初始几何缺陷拱的弹性承载力评估方法；易壮鹏[10]将几何缺陷拱的节点偏差视为随机变量，通过条件随机变量等方法得到了随机几何缺陷的分布方式和大小，同时从虚功原理和广义变分原理出发，研究了几何缺陷对拱的稳定性能的影响；Zhao等[11]提出了考虑平面几何缺陷的横向支撑拱的平面内弹性强度设计公式，证明了几何缺陷的大小和分布可能会导致拱的平面外强度减少。以上研究表明：针对初始缺陷对拱稳定性影响的研究，目前大多采用数值假设、人为施加缺陷的方式，与实际结构缺陷存在一定的差异，且未通过实验验证。

关于考虑初始缺陷拱失稳的实验研究，国内外学者鲜有所涉及。Papangelis等[12-13]建立了双对称截面圆拱的弯扭屈曲理论，导出了轴向和剪切应变的非线性表达式，并将其代入总势能的二阶变化式，得到了拱屈曲方程。同时，进行了拱顶集中力作用下的铝合金工字型截面拱的面外弹性弯扭失稳实验，测试了集中荷载作用下简支拱的弯扭失稳行为。Guo等[14]通过弹塑性试验研究发现固接钢拱的非弹性失稳承载能力受初始缺陷大小和分布的影响较大，但实验未获得不稳定平衡路径以及后屈曲失稳行为。La Poutré D B等[15]对15组拱顶集中作用力下工字型截面圆弧钢拱的面外弹塑性失稳进行了实验研究，拱的圆心角从90°变化到180°。实验表明，面外几何缺陷对拱极限承载能力大小有一定的影响。本文自行设计了位移控制加载系统，利用光学动态位移三维测量系统测得拱的实际初始几何缺陷，跟踪了拱顶集中力加载全过程的结构变形情况和失稳模态，分析了初始缺陷对拱失稳极值点和失稳模态的影响。

1 试验介绍

1.1 实验试件

本文研究对象为圆弧拱，如图1(a)所示。圆弧拱矢跨比为1/5、1/6、1/7和1/8，跨径为173 cm，拱截面为矩形截面，宽度和高度分别为25和1.5 mm，材质是牌号6 061的铝合金。通过拉伸试验测得铝合金弹性模量为6.8×1010Pa，圆弧拱试件经冷加工成形。为实现拱脚固接，本实验将圆弧拱的拱脚伸入到特殊加工的夹具，如图1(b)所示。固定和扭紧螺栓，确保拱脚与固定夹具无相对滑移。

图1 圆弧拱试件及拱脚夹具Fig.1 Specimens of circular arch and support lofting

1.2 初始线形和缺陷测试

采用NDI Optotrak光学动态位移三维测量系统进行实时位移测量。为精确获得试验拱的初始缺陷、线形、加载过程中的变形情况和初始屈曲、后屈曲失稳模态，在试验拱的拱脚、二分点、四分点、八分点和十六分点粘贴Markers反光标识点，共设17个标识点，如图2所示。Markers点是光学动态位移测试仪的三维测量系统配套的红外线发光标识点，具有质量轻、显示位置准确的特点。Markers点对圆弧拱变形的影响可忽略不计，NDI Optotrak光学动态位移三维测量系统的精度可达到0.1 mm，故实验仪器精度完全可以满足测量精度要求。

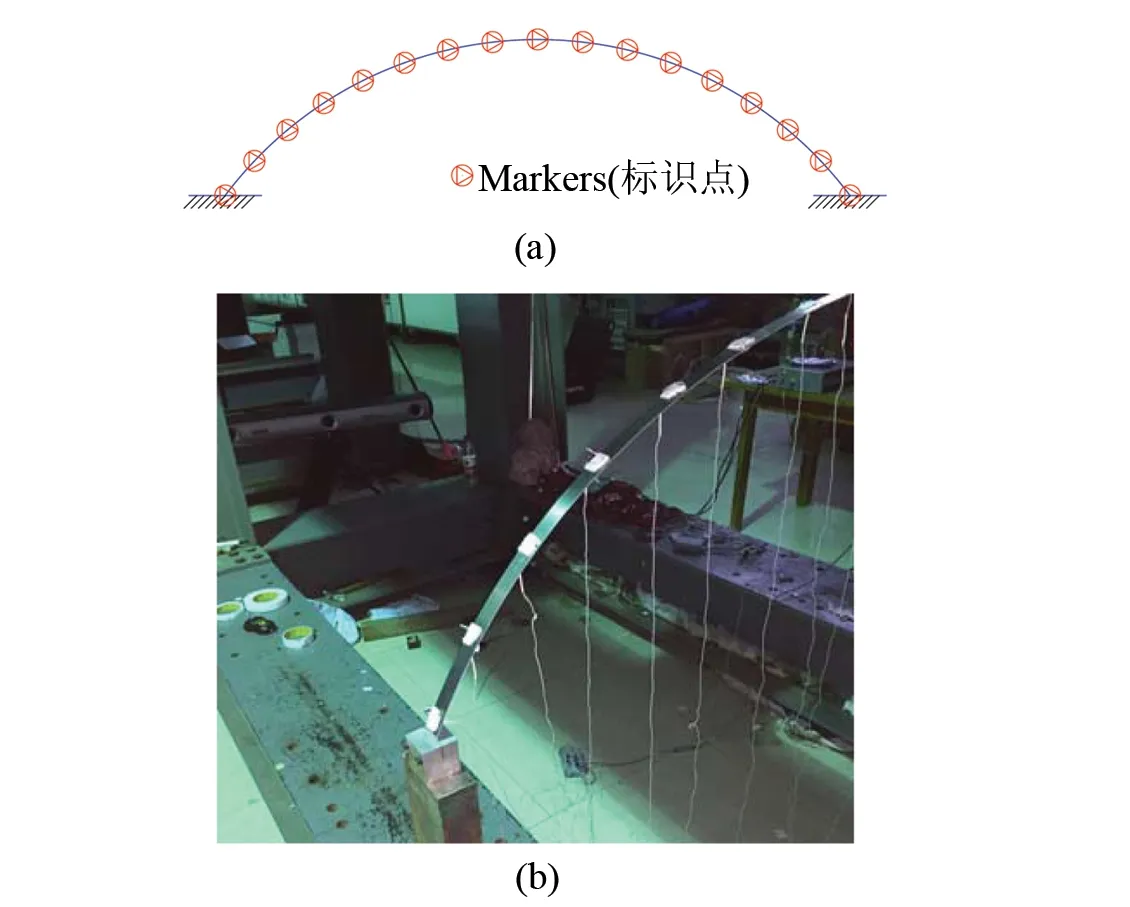
图2 Markers(标识点)位置示意图Fig.2 Marker points on the arch

实验开始前先对矢跨比为1/5～1/8的圆弧拱的初始状态进行了测量，包括圆弧拱的弧长、跨径、矢跨比和关键点三维空间坐标，以获得拱的初始线性以及初始缺陷，并与理想状态拱的线形进行比较。不同矢跨比的圆弧拱的实际拱与理想拱轴线，如图3所示。

由图3可知，由于加工、运输等各种原因，导致圆弧拱的实际线形与理想线形有着细微的差别。当矢跨比为1/5和1/6时，实际拱轴线比理论高出1.2%；当矢跨比为1/7时，实际拱轴线与理想拱轴线误差不到1%，伴随明显的正弦缺陷；当矢跨比为1/8时实际拱轴线拱顶比理想拱低了1.3%。

1.3 加载过程测试

为了获得整个实验过程中力和位移的关系曲线、失稳平衡路径，以及拱失稳的上下极值点，本文特别设计了一套位移控制加载装置。加载装置由力传感器、加载端固定夹片、拉杆和竖向自由伸缩平台组成。力传感器焊接在加载端固定夹片下方，将其紧贴于圆弧拱的拱顶中心处，并与下端拉杆相连接，最后将拉杆固定在竖向自由伸缩平台上，如图4所示。

图3 不同矢跨比圆弧拱实际拱轴线与理想拱轴线Fig.3 Practical axis and perfect axis of circular arches with different rise-span ratio

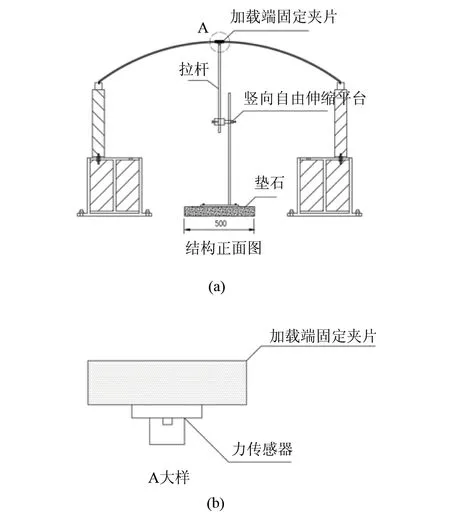
图4 位移加载装置Fig.4 Displacement loading device

在实验过程中，通过旋动拉杆与竖向自由伸缩平台间的螺栓，控制拱顶竖向位移值，并从力传感器中读出相应的荷载大小，如图5所示。实验第一阶段对圆弧拱采用位移控制的方式缓慢加载，记录每一加载步对应的力传感器和NDI Optotrak光学动态位移三维测量系统的读数，直到力传感器读数几乎不再增加，此时力传感器读数为曲线的上极值点；第二阶段继续通过位移控制进行加载，随着位移的增加，力传感器读数随之减少，直到力传感器读数几乎不再变化，此时力传感器读数为曲线的下极值点；当力传感器读数开始再次上升时，随即进入第三阶段，继续施加载荷，记录相关的数据，即可获得完整的荷载位移曲线。

图5 试验拱测试Fig.5 Arch in loading process

2 拱的有限元计算模型

为了验证实验结果的准确性、分析初始缺陷对拱失稳行为的影响，利用有限元软件ANSYS对具有相同矢跨比、跨径的理想状态圆弧拱进行数值模拟分析。采用平面梁单元beam3进行模拟，共建立100个单元，拱两端边界条件为固接，如图6所示。

图6 拱有限元模型Fig.6 Finite element model of arch

3 讨论与分析

3.1 荷载位移曲线

以1/5矢跨比的圆弧拱的荷载-位移曲线为例，说明两端固接的圆弧拱的失稳过程。如图7所示，拱顶竖向集中力从零开始，拱顶竖向位移与荷载曲线沿着稳定平衡路径0A逐渐上升，到达上极值点A时，拱结构发生前屈曲失稳；若继续施加拱顶竖向位移，拱顶集中力将沿着非稳定平衡路径AB逐渐减少，此时拱失去了承载能力；当到达下极值点B时，拱发生后屈曲失稳；若继续增加拱顶竖向位移，则拱顶集中力又继续沿稳定平衡路径BC逐渐增大，拱重新恢复了承载能力。平衡曲线的上下两个极值点A和B对应的荷载即为前屈曲和后屈曲失稳临界荷载。

图7 1/5矢跨比的圆弧拱拱顶荷载-位移曲线Fig.7 Loading-displacement curvels on the crown of circular arch with 1/5 rise-span ratio

图8为1/5～1/8矢跨比的圆弧拱拱顶竖向位移-荷载曲线，涉及FEM计算值与实测数据两组曲线。从图8中的(a)～(d)可知， FEM数值模拟和实验测试结果，拱的前屈曲和后屈曲失稳极值点均是随着矢跨比的减小而降低；同时，实测上极值点均位于理想FEM计算极值点下方。实测曲线的上极值点均略低于理想FEM数值模拟结果，说明初始几何缺陷对拱的承载能力影响较大，降低了其承载能力。

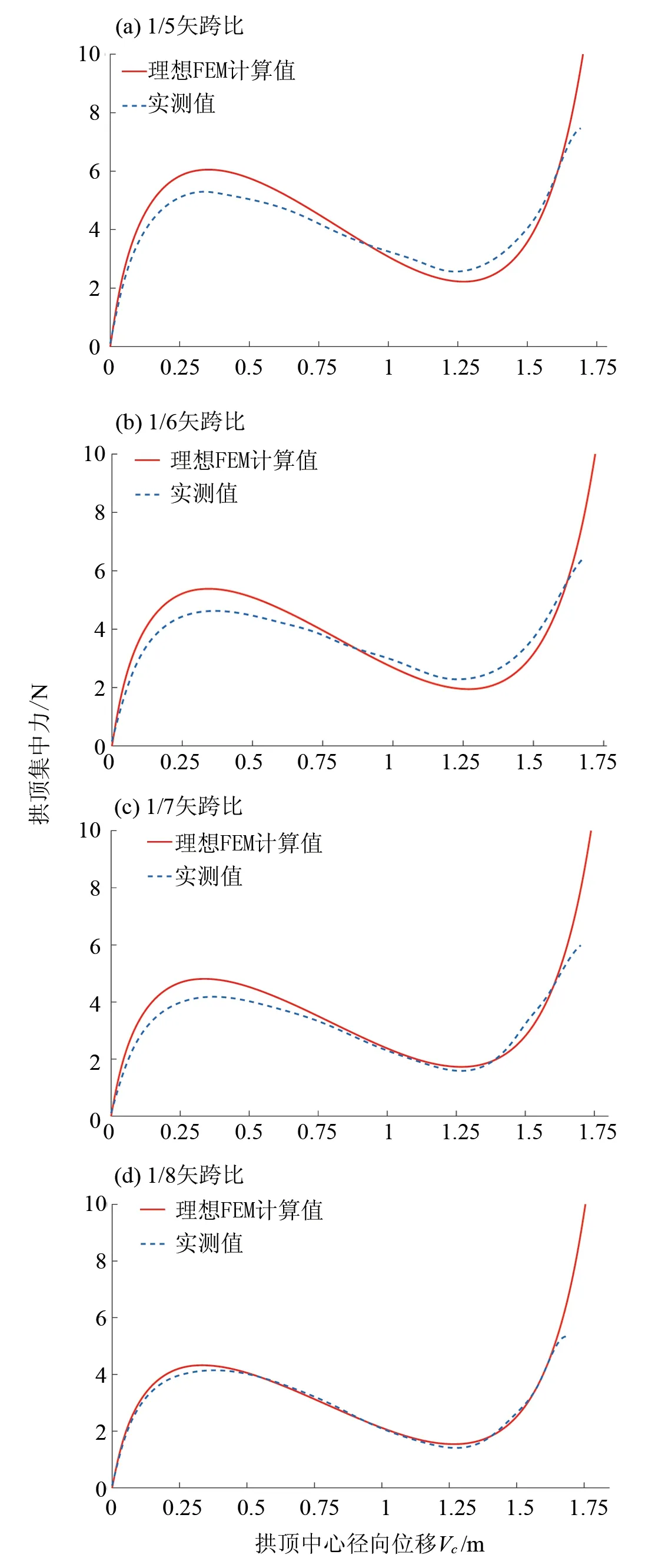
图8 不同矢跨比的圆弧拱拱顶荷-载位移曲线Fig.8 Loading-displacement curvels on the crown of circular arches with different rise-span ratio

图9为不同矢跨比的圆弧拱的失稳临界荷载。由图9可知，前屈曲失稳极值点远大于后屈曲失稳极值点，且前屈曲失稳极值点为后屈曲极值点的2～2.5倍。

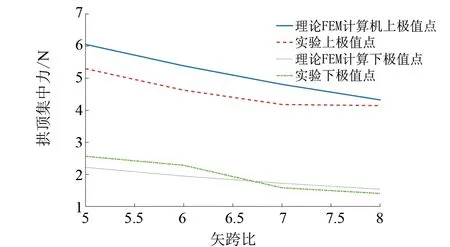
图9 不同矢跨比的圆弧拱的失稳临界荷载Fig.9 Instability critical load of circular arch with different rise-span ratio

3.2 失稳模态

通过对拱轴线17个Mark点的实时观测，可跟踪整个加载过程中拱的变形形态，准确捕捉到拱的前屈曲和后屈曲失稳模态。如图10-13所示，经过多组实验对比发现，不同矢跨比、不同初始几何缺陷拱的屈曲失稳模态均有不同，但总体上均呈马鞍形。

图10 1/5矢跨比圆弧拱屈曲失稳模态Fig.10 The buckling mode of circular arch with 1/5 rise-span ratio

图11 1/6矢跨比圆弧拱屈曲失稳模态Fig.11 The buckling mode of circular arch with 1/6 rise-span ratio

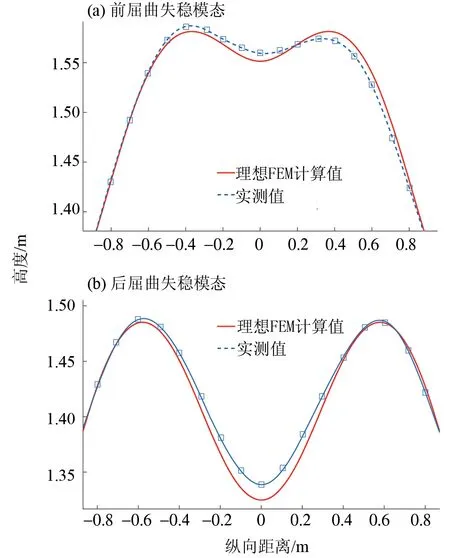
图12 1/7矢跨比圆弧拱屈曲失稳模态Fig.12 The buckling mode o of circular arch with 1/7 rise-span ratio

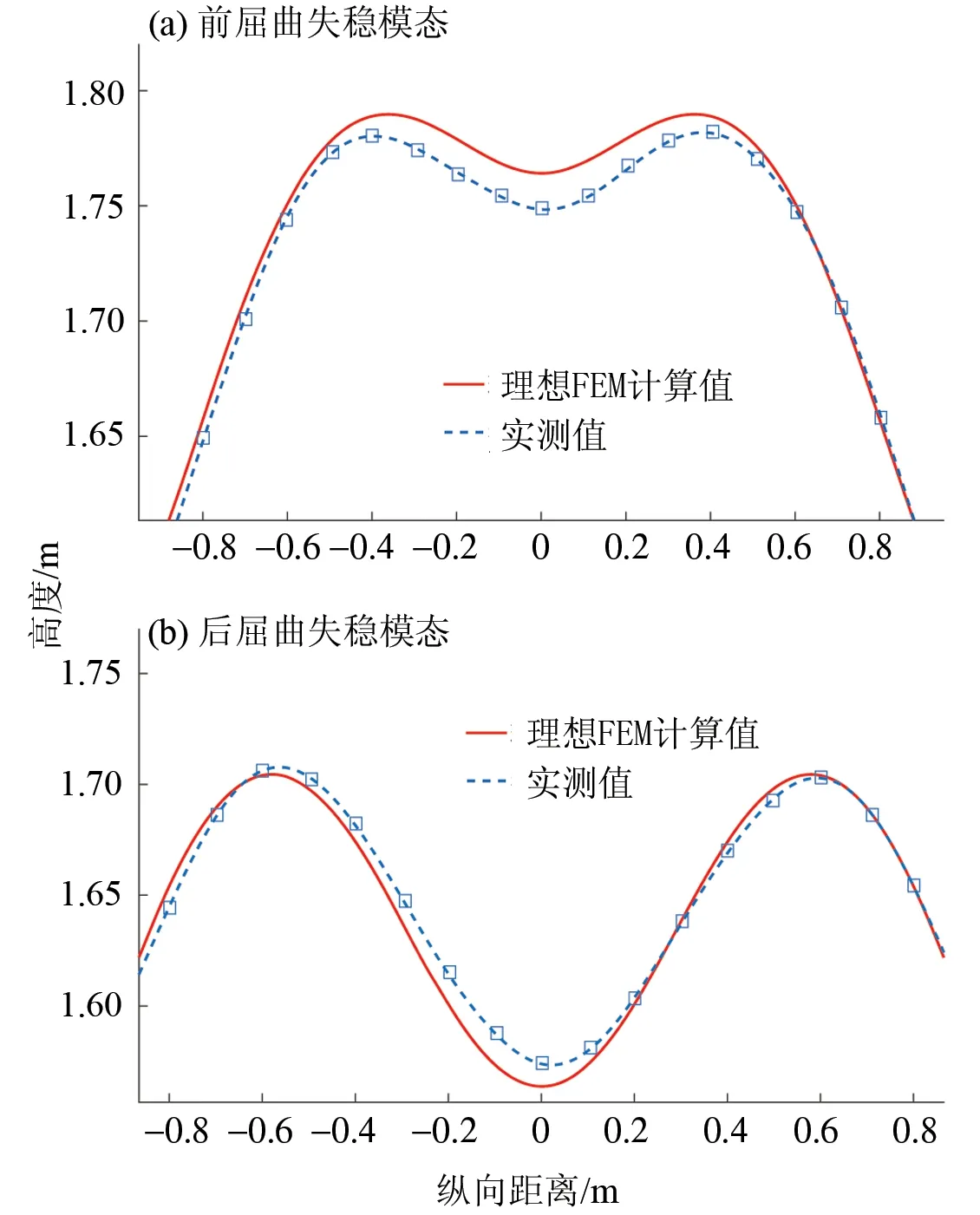
图13 1/8矢跨比圆弧拱屈曲失稳模态Fig.13 The buckling mode of circular arch with 1/8 rise-span ratio

对比实测数据和FEM数值计算结果发现，计算结果与实验测试结果有一定差异。对于前屈曲失稳模态，理想的FEM数值计算结果均为正对称曲线，而实测结果并非严格对称；特别地，1/6矢跨比的圆弧拱的实测失稳模态呈现反对称的趋势。这主要是因为拱的初始几何缺陷和拱顶集中力加载点与理论对称点略有偏差所致。对于后屈曲失稳模态，理想FEM数值计算结果与实测值基本吻合，曲线变化趋势基本一致，均呈对称变形状态，说明拱的初始几何缺陷对后屈曲失稳模态的影响较小。

4 结 论

本文对圆弧拱加载全过程的力-位移曲线及失稳模态进行了实时测量，跟踪了加载全过程中圆弧拱的变形情况和失稳模态，获得了拱的失稳平衡路径，获得了缺陷圆弧拱的失稳上极值点和下极值点，揭示了初始几何缺陷对拱极值点以及屈曲失稳模态的影响。主要结论如下：

1)本文自行设计的位移控制加载装置，可实现圆弧拱由非线性平衡状态到非平衡状态的全过程加载。

2)拱结构前屈曲和后屈曲极值点均是随着矢跨比的减小而降低，并且前屈曲失稳极值点远大于后屈曲失稳极值点；前屈曲失稳极值点对拱的初始几何缺陷比较敏感，初始几何缺陷会降低拱的承载能力。

3)初始几何缺陷对拱的前屈曲失稳模态的影响大于后屈曲失稳模态。

参考文献：

[1] BRADFORD M A, UY B, PI Y L. In-plane elastic stability of arches under a central concentrated load[J]. Journal of Engineering Mechanics, 2002, 128(7):710-719.

[2] LIU A R，HUANG Y H，YU Q C，et al. An analytical solution for lateral buckling critical load calculation of leaning-type arch bridge[J]. Mathematical Problems in Engineering, 2015, 2014(3):1-14.

[3] LIU A R，HUANG Y H，FU J Y，et al. Experimental research on stable ultimate bearing capacity of learning-type arch rib systems[J]. Journal of Constructional Steel Research, 2015, 114: 281-292.

[4] LIU A R，LU H W，FU J Y，et al. Analytical and experimental studies on out-of-plane dynamic instability of shallow circular arch based on parametric resonance[J]. Nonlinear Dynamics, 2017, 87:677-694.

[5] 李康杰,刘爱荣,卢汉文,等.圆弧浅拱面外动力稳定性实验研究[J]. 中山大学学报(自然科学版), 2015,54(3):30-35.

LI Kangjie, LIU Airong, LU Hanwen, et al. Experimental study on out-of-plane dynamic stability of circular shallow arch[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2016, 54(3):30-35.

[6] 颜全胜, 骆宁安, 韩大建,等. 大跨度拱桥的非线性与稳定分析[J]. 华南理工大学学报, 2000, 28(6) : 64-68.

YAN Quansheng, LUO Ningan, HAN Dajian, et al. Nonlinearity and stability analysis for a long-span arch bridge [J]. Journal of South China University of Technology, 2000, 28(6) : 64-68.

[7] 程进,江见鲸,肖汝诚,等. 大跨度拱桥极限承载力的参数研究[J]. 中国公路学报,2003,16(2): 45-47.

CHEN Jin, JIANG Jianjing, XIAO Rucheng, et al. Parametric study of ultimate capacity of long-span arch bridges [J]. China Journal of Highway and Transport, 2003,16(2): 45-47.

[8] 谢旭,李辉,黄剑源. 大跨度两铰钢拱桥面内稳定分析[J]. 土木工程学报,2004,37(8): 43-49.

XIE Xu, LI Hui, HUANG Jianyuan, Study on in-plane stability of long-span two-hinged steel arch bridges[J]. China Civil Engineering Journal, 2004,37(8): 43-49.

[9] 戴云峰. 具有任意初始几何缺陷的圆弧拱弹性稳定分析研究[D]. 哈尔滨:哈尔滨工业大学,2004:1-5.

DAI Yunfeng. Study on elastic stability analysis of circular arcs with arbitrary initial geometric imperfections[D]. Harbin: Harbin Institute of Technology, 2004:1-5.

[10] 易壮鹏. 几何缺陷对拱结构力学性能的影响[D]. 长沙：湖南大学, 2007.

YI Zhuangpeng. The effect of geometric defects on the mechanical properties of arch structures[D]. Changsha: Hunan University, 2007.

[11] ZHAO S Y，GUO Y L，DOU C. Geometric imperfection effects on out-of-plane inelastic buckling loads of lateral braced arches [C]//Pacific Structural Steel Conference Beijing: China Building Materials Press, 2013:181-186.

[12] PAPANGELIS J P，TRAHAIR N S. Flexural-torsional buckling of arches [J]. J Struct Eng, 1986, 112(11): 2494-2511.

[13] PAPANGELIS J P，TRAHAIR N S. Flexural-torsional buckling test on arches [J]. J of Struct Eng, 1987, 113(4): 889-906.

[14] GUO Y L，ZHAO S Y，PI Y L，et al. An experimental study on out-of-plane inelastic buckling strength of fixed steel arches[J]. Engineering Structures, 2015, 98:118-127.

[15] LA POUTRé D B，SPOORENBERG R C，SNIJDER H H，et al. Out-of-plane stability of roller bent steel arches-an experimental investigation[J]. Journal of Constructional Steel Research, 2013, 81:20-34.

[16] 刘爱荣,李晶,黄永辉. 拱的静动力稳定性研究进展[J]. 广州大学学报(自然科学版), 2016,15(5):1-12.

LIU Airong, LI Jing, HUANG Yonghui. Research progress on static and dynamic stability of arches[J]. Journal of Guangzhou University(Natural Science Edition) , 2016,15(5):1-12.

[17] LIU A R，LU H W，FU J Y，et al. Lateral-torsional buckling of fixed circular arches having a thin-walled section under a central concentrated load[J]. Thin-Walled Structures, 2017, 118:46-55.