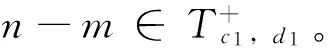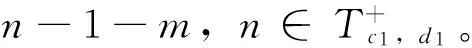整数区间上长极小零和序列的结构*
2018-04-23邓贵新曾祥能
邓贵新,曾祥能
(1. 广西师范学院数学与统计科学学院,广西 南宁 530001;2. 中山大学中法核工程与技术学院, 广东 珠海 519082)
令G是一个交换群(运算记为加法),G0是G的非空子集。G0上的一个序列是一个有限序列,其中的元素都包含在G0中。称一个非空序列为零和的,如果此序列的项加起来等于群G的单位元0。称一个零和序列为极小零和的,如果它的任意非空真子序列都不是零和序列。
极小零和序列是零和理论的主要研究对象之一。此理论与群论,图论,拉姆齐理论,以及分解理论有紧密的联系[1-3]。零和理论中两个重要问题就是计算Davenport常数和刻画极小零和序列的结构,其中G0上的Davenport常数D(G0)定义为G0上的极小零和序列所能达到的最大长度。
Davenport常数是以数学家Davenport的姓名所命名。在20世纪60年代,Davenport在研究代数整数环上的分解问题时,考虑了如下问题:代数整数环上一个不可约元分解成素理想的乘积时,这些素理想最多有多少个(把重数算入)?而此最大个数就是这个代数整数环的类群的Davenport常数,由此开启了这方面的研究。
当G是有限交换群时,人们在这两个问题上取得了不少进展。现在我们已经知道了秩不大于2的有限交换群以及有限交换p-群的Davenport常数。在极小零和序列的结构方面, 当G是一个有限循环群时, 我们已经知道许多结果[4-7]。当G是秩为2的有限交换群时,我们只知道达到最大长度即D(G)的极小零和序列的结构[8-9]。当G是一些结构比较简单的交换群时,也有一些更进一步的结论[10]。

1 记号与术语
我们将使用文[2]一书中的记号。令N与Z分别为自然数集与整数集。对所有实数x和y,令[x,y]={i∈Z:x≤i≤y}。
令G是一个交换群(运算记为加法),G0是G的非空子集。G0上的一个序列是一个有限序列,其中的元素都包含在G0中。我们把G0上的序列看成是由G0生成的交换自由群胚F(G0)中的元素。显然F(G0)中的单位元就是空序列。一般地把G0中的一个序列写为

如果S是整数集上一个序列,那么记S+,S-分别为由S的大于0,小于0的部分构成的序列。 称T为S的一个子列,如果vg(T)≤vg(S)对任意g∈G0成立,此时记为T|S。称S的一个子列T为真子列,如果T≠S。集合
∑(S)={σ(T):T|S,T非空}
称为S的和集。
一个序列S称为
零和,如果σ(S)=0。
极小零和,如果σ(S)=0,并且对S所有非空真子列T有σ(T)≠0。
用A(G0)记G0上的由所有极小零和序列构成的集合,并定义G0的Davenport常数为
由于整数上的零和序列和有限循环群上的零和序列有着密切联系,我们引入如下概念。 设n∈N,我们称Z上的一个序列S是模n零和(模n极小零和), 如果φn(S)在Zn中是零和(极小零和),其中φn:Z→Zn是标准同态。设S是整数集上的一个序列,我们有下面的关于零和与模n零和之间的联系。
如果S是零和的,那么S是模n零和的。反之不一定对。
如果S是极小零和的,那么S是模n零和的,但不一定是模n极小零和的。
如果S是模n极小零和的并且σ(S)=kn,k>0,那么(-n)[k]·S是极小零和的。
2 一些引理
在本节中,我们研究整数上的极小零和序列的一些性质。 若极小零和序列S包含0, 则S=0,而且此序列是唯一的长度为1的极小零和序列。因此,为了避免平凡情形,在本节中我们总是假设所考虑的极小零和序列的长度都至少为2,特别地,此序列不包含0。
引理1[14]设S是整数上的一个极小零和序列并且令
max(S)=n,min(S)=-m。那么有u≤n,v≤m且uv≤σ(S+)=-σ(S-)。
推论1 设S是整数上的一个极小零和序列并且令
max(S)=n,min(S)=-m。
(i) 如果u=n,那么有S+=n[v],且S-是模n极小零和的;
(ii) 如果v=m,那么有S-=(-m)[u],且S+是模m极小零和的。
证明由结论的对称性只需要证明(i)。设S+=b1…bv,其中bi∈[1,n]。由引理1,nv≤σ(S+)=b1+…+bv≤nv。因此,b1=…=bv=n,即S+=n[v]。
若T是S-的一个模n零和子列且σ(T)=-kn,k∈N。那么
0<-σ(T)≤-σ(S-)=σ(S+)=nv
可得1≤k≤v,这样T·n[k]就是S的一个零和子列。 由于S是极小的,马上得到并且。因此S-是模n极小零和的。证毕。
引理2 (i)设n∈N,S是整数上一个长度为n的模n极小零和序列,则存在与n互素的整数k,使得S中每一项都模n同余于k。
(ii) 设n≥3,S是整数上一个长度为n-1的模n极小零和序列,则存在与n互素的整数k,使得S中有n-2项都模n同余于k。
证明此结论众所周知。文[5-6]推广了此结论。
3 主要结论
在本节,我们证明本文的主要结论,即刻画区间[-m,n]上长度至少为n+m-2的极小零和序列。长度为n+m的极小零和序列的结构已经在[12]中刻画了。
定理1[12]设S为[-m,n]上的一个长度为n+m的序列。则S是极小零和序列当且仅当gcd(n,m)=1且S=(-m)[n]·n[m]。
现在,将分别刻画长度为n+m-1与n+m-2的极小零和序列。
定理2 设m+n≥3,S为[-m,n]上一个长度为n+m-1的序列。则S是极小零和序列当且仅当以下之一成立:
(i)S=(-m)[n-1]·(n-1)[m],gcd(m,n-1)=1,n≥2;
(ii)S=(-m)[n-1]·n[m-1]·(n-m),gcd(m,n)=1,n≠m;
(iii)S=(-m+1)[n]·n[m-1],gcd(m-1,n)=1,m≥2。
证明首先,容易验证上述3个序列都是极小零和的。现在假设S是极小零和的。令
由引理1有u≤n,v≤m。结合u+v=m+n-1,有(u,v)=(n,m-1)或(n-1,m)。
如果vn(S)=0或v-m(S)=0,那么S是[-m,n-1]或[-m+1,n]上的极小零和序列。这样就归结到了定理1,在定理1中用n-1代替n或者用m-1代替n,就得到S=(-m)[n-1]·(n-1)[m]或S=(-m+1)[n]·(n)[m-1]。
下设min{vn(S),v-m(S)}≥1,分如下两个子情形。
情形1 (u,v)=(n-1,m)。 由推论1,S-=(-m)[n-1]且S+是一个长度为m的模m极小零和序列。又因为n∈S+,由引理2,gcd(n,m)=1且S+的每一项都模m同余于n。 令S+=b1…bm, 其中bi∈[1,n]。则
m(n-1)=σ(S+)=b1+…+bm≤mn
且bi≡n(modm)。因此,S+的项bi中有m-1个等于n,还有一个等于n-m>0,即S=(-m)[n-1]·n[m-1]·(n-m)。
情形2 (u,v)=(n,m-1)。用情形1中同样的讨论知S+=n[m-1],S-=(-m)[n-1]·(-m+n),n-m<0。则S=(-m)[n-1]·n[m-1]·(n-m)。
下面将证明最后一个主要定理。由于对称性,不妨假设1≤m≤n。
定理3 设1≤m≤n,m+n≥5,S为[-m,n]上一个长度为n+m-2的序列。则S是极小零和序列当且仅当以下之一成立:
(i)S=(-m)[n-2]·(n-2)[m],gcd(m,n-2)=1;
(ii)S=(-m)[n-2]·(n-1)[m-1]·(n-1-m),gcd(m,n-1)=1;
(iii)S=(-m)[n-2]·n[m-1]·(n-2m),gcd(m,n)=1,n≠2m;
(iv)S=(-m)[n-2]·n[m-2]·(n-m)[2],gcd(m,n)=1,n>m≥2;
(v)S=(-m+2)[n]·n[m-2],gcd(m-2,n)=1,m≥3;
(vi)S=(-m+1)[n-1]·(n-1)[m-1],gcd(m-1,n-1)=1,m≥2;
(vii)S=(-m+1)[n-1]·n[m-2]·(n-m+1),gcd(m-1,n)=1,m≥2;
(viii)S=(-1)[n-2]·(-2)·n,m=2。
证明首先容易验证上述所有序列都是极小零和的。再假设S是极小零和的。令
由引理1有u≤n,v≤m。结合u+v=m+n-2,有(u,v)=(n-2,m),(n,m-2)或(n-1,m-1)。
情形1 (u,v)=(n-2,m)。 由推论1,S=(-m)[n-2]·S+,且S+是一个长度为m的模m极小零和序列。令S+=b1…bm, 其中bi∈[1,n]。不妨设b1≤…≤bm。由引理2,gcd(bm,n)=1且对任意i∈[1,m]有bi≡bm(modm)。还有
m(n-2)=σ(S+)=b1+…+bm≤mbm
如果bm≤n-2,则b1=…=bm,即条件(i)成立。
如果bm=n-1,则b1=n-1-m>0,b2=…=bm=n-1,即条件(ii)成立。
如果bm=n,则b1=n-2m>0,b2=…=bm=n;或者m≥2,b1=b2=n-m>0 ,b3=…=bm=n。因此条件(iii)或条件(iv)成立。
情形2 (u,v)=(n,m-2) 此情形的证明与情形1相同。可得如下4种情形:
①S=(-m+2)[n]·n[m-2],gcd(m-2,n)=1,m≥3。即条件(v)成立。
②S=(-m+1)[n-1]·(-m+1+n)·n[m-2],gcd(m-1,n)=1,m≥3,m-1>n。与m≤n矛盾。
③S=(-m)[n-1]·(-m+2n)·n[m-2],gcd(m,n)=1,m≥3,m>2n。与m≤n矛盾。
④S=(-m)[n-2]·n[m-2]·(n-m)[2],gcd(m,n)=1,m≥2,n 情形3 (u,v)=(n-1,m-1)。此时n,m≥2。设 S-=(-m)[a]·(-m+1)[b]·(-α1)…(-αk), S+=β1…βt·(n-1)[c]·n[d] 其中αi∈[1,m-2],βj∈[1,n-2],k,t≥0。 如果a=0,则S是[-m+1,n]上长度为n+(m-1)-1的极小零和序列。在定理2中,用m-1替换m,可得 ⑤S=(-m+1)[n-1]·(n-1)[m-1],gcd(m-1,n-1)=1,m≥2。即条件(vi)成立。 ⑥S=(-m+1)[n-1]·n[m-2]·(n-m+1),gcd(m-1,n)=1,m≥2。即条件(vii)成立。 ⑦S=(-m+2)[n]·n[m-2],gcd(m-2,n)=1,m≥3。与(u,v)=(n-1,m-1)矛盾。 如果d=0, 则S是[-m,n-1]上长度为(n-1)+m-1的极小零和序列。在定理2中,用n-1替换n,可得 ⑧S=(-m)[n-2]·(n-2)[m],gcd(m,n-2)=1,m≥2。与(u,v)=(n-1,m-1)矛盾。 ⑨S=(-m)[n-2]·(n-1)[m-1]·(n-1-m),gcd(m,n-1)=1,n-1≠m。由于(u,v)=(n-1,m-1),可得n-1-m<0。再由n≥m,可得n=m。即条件(ii)成立,且n=m的情形。 ⑩S=(-m+1)[n-1]·(n-1)[m-1],gcd(m-1,n-1)=1,m≥2。即条件(vi)成立。 因此, 我们现在假设min{a,d}≥1。由于极小零和序列S的长度至少是3,所以m 如果a≥c+d,我们把S+中的n以及n-1均与一个-m加起来得到另一个极小零和序列 T=(-m)[a-c-d]·(-m+1)[b]·(-α1)…(-αk)· 其中T-的长度为 n-1-c-d=n-1-(m-1-t)=n-m-t T+的长度为m-1。对序列T应用引理1,可得 (n-m+t)(m-1)≤β1+…+βt+ c(n-1-m)+d(n-m)≤ t(n-2)+c(n-1-m)+ (m-1-t-c)(n-m)= t(m-2)-c+(m-1)(n-m)= (m-1)(n-m+t)-t-c 因此t=c=0,d=m-1,也即S+=n[m-1],此时S-是长度为n-1的模n极小零和序列。由引理2,S-中有n-2项都是模n同余的。再由S-的项都是在[-m,-1]中,且m≤n,可得S-=(-g)[n-2]·h,其中g,h∈[1,m]。若g≤m-1,则 (m-1)n=-σ(S-)=(n-2)g+h≤ (n-2)(m-1)+m=(m-1)n-m+2≤ (m-1)n 因此上述不等式实际上都是等式,则m=2,g=m-1=1,h=m=2,也即条件(viii)成立。若g=m,则(m-1)n=-σ(S-)=(n-2)m+h。由此可得h=2m-n,即条件(iii)成立。 如果a 对Tc1,d1应用推论1,可得 则c=t=0,矛盾。 若t=0,此时有b=n-1-a,c=m-1-d, S=(-m)[a]·(-m+1)[n-1-a]· (n-1)[m-1-d]·n[d] 由于 参考文献: [1] GAO W, GERODINGER A. Zero-sum problems in finite abelian groups: A survey [J]. Expositiones Mathematicae, 2006, 24(4): 337-369. [2] GERODINGER A, HALTER-KOCH F. Non-unique factorizations: algebraic, combinatorial and analytic theory [M]. Boca Raton: Chapman & Hall/CRC, 2006. [3] GERODINGER A, RUZSA I. Combinatorial number theory and additive group theory, [M]. Basel: Birkhäuser, 2009. [4] 官欢欢,曾祥能,袁平之. 零和自由序列F(5)的刻画[J]. 中山大学学报(自然科学版),2010, 49(3): 1-4. GUAN H H, ZENG X N, YUAN P Z. Description of the invariant F(5) of zero-sum-free sequence[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2010, 49(3): 1-4. [5] SAVCHEV S, CHEN F. Long zero-free sequence in finite cyclic groups [J]. Discrete Mathematics, 2007, 307(22): 2671-2679. [6] YUAN P. On the index of minimal zero-sum sequences over finite cyclic groups [J]. Journal of Combinatorial Theory:Series A, 2007, 114(8): 1545-1551. [7] ZENG X, YUAN P, LI Y. On the structure of long unsplittable minimal zero-sum sequences [J]. Acta Arithmetica, 2016, 176(2): 131-159. [8] GAO W, GERODINGER A, GRYNKIEWICZ D. Inverse zero-sum problem III [J]. Acta Arithemetica, 2010, 141(2): 103-152. [9] REIHER C. A proof of the theorem according to which every prime number possesses property B [D]. Germany: University of Rostock, 2010. [10] 官欢欢,袁平之,C2⊕C2n上不可分原子的结构 [J].中山大学学报(自然科学版),2013, 52(5): 78-81. GUAN H H, YUAN P Z. The structure of unsplittable atoms overC2⊕C2n[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2013, 52(5): 78-81. [11] SAHS M, SISSOKHO P, TORF J. A zero-sum theorem overZ[J].Integers, 2013, 13: A70. [12] PLAGNE A, TRINGALI S. The Davenport constant of a box [J]. Acta Arithmetica, 2015, 171(3): 197-219. [13] DENG G, ZENG X. Long minimal zero-sum sequences over a finite subset ofZ[J]. European Journal of Combinatorics, 2018, 67: 78-86. [14] SISSOKHO P. A note on minimal zero-sum sequences overZ[J]. Acta Arithmetica, 2014, 166(3): 279-288.
β1…βt·(n-1-m)[c]·(n-m)[d]