小学数学《三角形的内角和》课例研究

李织兰 杨起群 蒋晓云 冯涛励

【摘要】本文根据数学课程标准的要求，结合课例论述教师在小学阶段教学“三角形的内角和为180°”时启蒙学生理性精神、培养其推理意识的途径，提出结合“帕斯卡的推理”引导学生论证三角形内角和为180°的教学策略。

【关键词】三角形内角和 理性精神 演绎推理 “帕斯卡的推理”

【中图分类号】G 【文献标识码】A

【文章编号】0450-9889（2018）12A-0030-03

2005年3月初，姜伯驹院士在全国政协会议上的提案中指出，“三角形内角和等于180°”这样的基本定理，只让学生用测量、计算、拼接实验的方法“归纳猜想，发现规律（结论）”，不说理，不证明，数学课就失去了理性的精神。反思这十多年的小学数学课程改革，小学数学教学淡化了数学中的逻辑推理、理性思维。所以，经过修订的《义务教育数学课程标准》（2011版）明确要求：在第一学段和第二学段，可以逐渐渗透给学生知道，合情推理的结论可能是正确的，也可能是错误的，还需要依靠演绎推理去证明或者证否。

我们选取人教版数学四年级下册《三角形的内角和》一课，以在小学数学教学中“启蒙理性精神，初步培养学生演绎推理的意识和推理能力”为主题进行课例研究。

一、教学内容与素材分析

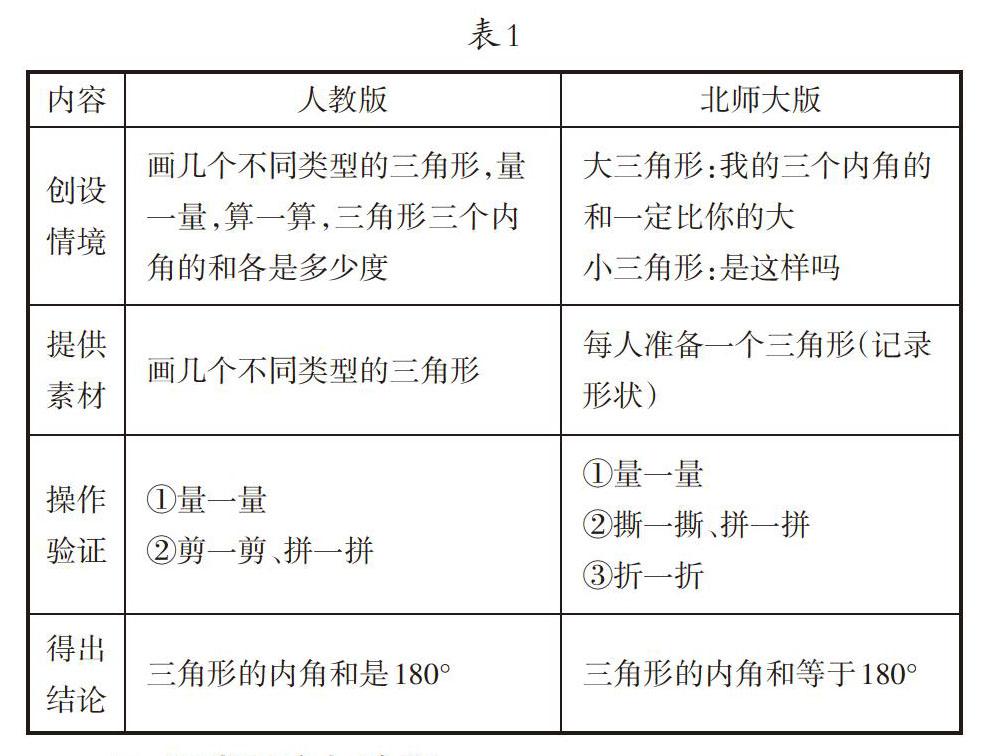
人教版、北师大版小学数学教材中的《三角形的内角和》这一教学内容，都有“操作验证”“得出结论”环节。操作验证主要包括两个环节，分别是“量一量”和“拼一拼”。

二、课堂观察与诊断

我们选取一节小学数学优质课的视频作为课堂观察材料，进行课堂观察与诊断。

（一）教学片段

教师在探究“三角形的内角和是180度”这一环节，设计了四个步骤：量角求和、拼折验证、课件展示、归纳小结，让学生在“量一量”“拼一拼”“折一折”的实验操作过程中，探究从不同的途径验证结论和解决问题的方法。

其中，在归纳小结中出现下面这样一个小片段。

师：我们刚才用了这么多种方法来验证，现在我们可以肯定地说，三角形的内角和是180°。请同学们用肯定的语气来读一读这句话。

生（齐读）：三角形的内角和是180°。

（二）教学诊断

“我们刚才用了这么多种方法来验证，现在我们可以肯定地说：三角形的内角和是180°。”真的只通过“量一量”“拼一拼”“折一折”就能肯定“每一个三角形的内角和都等于180°”吗？不能！实验归纳的结果不一定靠谱，用这种方法得到的结论可能是对的，也可能是错的，还需要依靠演绎推理去验证。

虽然小学阶段关注通过合情推理发现结论，培养演绎推理能力是中学几何教学的核心追求。但是，如果小学阶段不说理、不证明、不启蒙学生的理性精神，甚至错误地完全肯定实验归纳所得到的结论，到了初中阶段学习“三角形内角和定理”的证明时，学生会认为完全没有必要。

在学习“三角形的内角和等于180°”这样的基本结论时，教师让学生用测量、计算、拼接实验的方法“归纳猜想，发现规律（结论）”是没有错误的，但教师最后小结的那段话是违背数学课程标准要求的严重错误。

（三）教学建议

教师可从“发现数学规律”和“启蒙理性精神”两方面改进教学。在总结发现的规律时，教师可以跟学生说：“我们刚才用了这么多种方法，现在我们发现（猜测）三角形的内角和是180°。”随后给出一些“测量会产生误差”“从特殊到一般归纳不一定完全”和“眼见未必为实”的例子，让学生明白“实验归纳的结果不一定靠谱”，所以只通过“量一量”“拼一拼”“折一折”的实验归纳是不能肯定“每一个三角形的内角和都是180°”的。教师再告诉学生：“2000多年前，数学家欧几里德写了一套名为《几何原本》的书，在他的书中，用‘逻辑推理的方法对这个结论作了证明，从而保证了每一个三角形内角和都等于180°，现在我们可以相信它是对的。这个证明方法我们将会在初中阶段学习。”

三、课堂改进

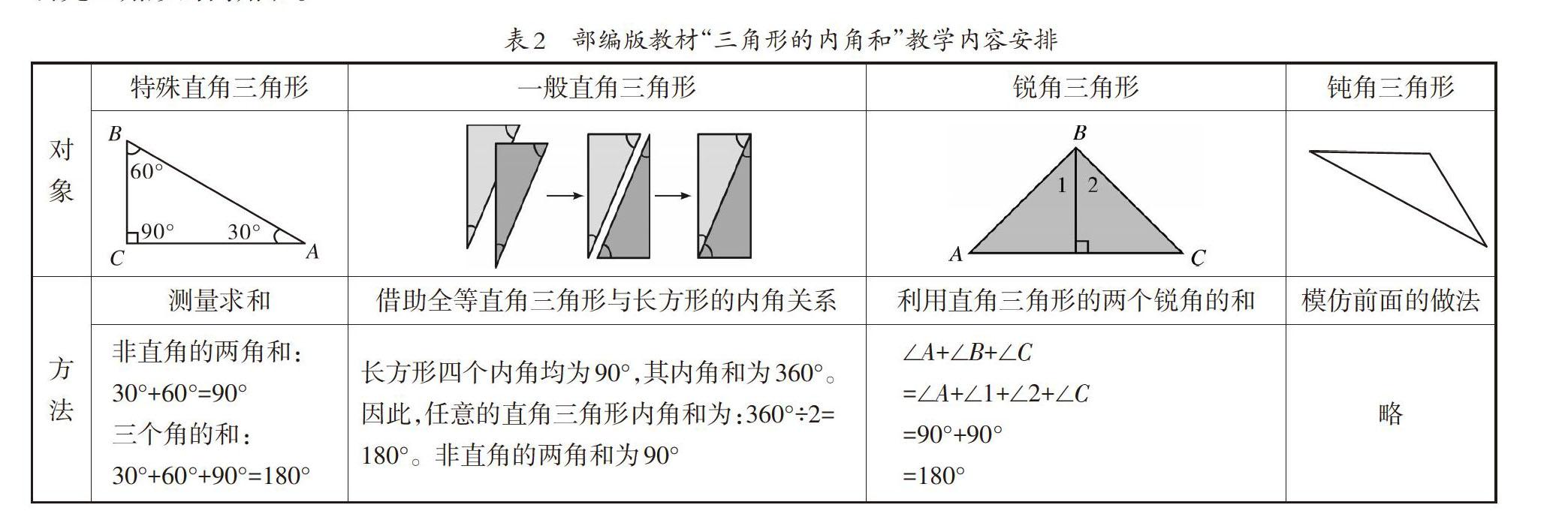
数学证明能力的形成往往要经历许多年，需要从找到初步的感觉，到举例论证，再到一般的证明。我们主张在小学阶段开始让学生接触数学证明的思想。也正因为如此，我们吸收部编版教材采取的类似于少年帕斯卡首先使用的“推理论证”方法，帮助学生从理性的角度研究三角形的内角和。

广泛阅读各种教材，扬长避短，我们进一步优化《三角形的内角和》教学设计如下。

（一）创设情境，提出问题

教师通过“三种类型的三角形争论内角和大小（如图1）”的趣味情境作為导入，让学生作为“调解员”为它们解决争议，激发学生学习数学的兴趣，使其明白为什么教材要求“画几个不同类型的三角形，量一量，算一算”，很自然地进入新课学习。

（二）动手操作，合作探究

1.量一量

4人小组合作完成“量一量”“算一算”实验操作，由小组长向全班展示。教师及时点评，关注每个小组的结果，让学生阐述为什么选择不同类型的三角形，渗透“分类讨论”和“归纳”的思想，培养学生周密、严谨、有条理地思考问题的思维，引发猜想：三角形的内角和可能都是180°。

教师预设学生可能测量结果不一，鼓励学生汇报自己测量的真实数据，及时讨论产生误差的原因，让学生认识到出现误差是实验活动不可避免的现象，培养学生的科学态度。

2.拼一拼

“拼一拼”就是通过求“和角”是“平角”来说明三角形内角和是180°。“和角”是一个“数”，“平角”是一个“形”。我们安排了图2的操作来实现“量一量”与“拼一拼”之间的自然过渡，突出“拼一拼”的教育价值。

随后，教师引出问题“只有一个三角形，能否组成平角”，如图3。

（三）巧妙设疑，让学生真有思考

教师先通过实例让学生思考：“查看我们班的数学成绩册，我发现1号同学数学及格，2号同学数学及格，3号同学数学及格，4号同学数学及格，5号同学数学及格，6号同学数学及格，7号同学数学及格，8号同学数学及格，我就得到全班所有同学数学成绩及格。事实证明我是错的，为什么老师会做出错误的判断呢？”学生明白了我们只能对我们测量过的对象下结论，“从特殊到一般”的“实验归纳”并不完全。因此，通过“量一量”“拼一拼”不能保证每一个三角形的内角和都是180°。

接着，教师让学生观察图4，学生大多觉得∠AOB=180°，∠COD不等于180°，实际上，∠AOB=179.5°，∠COD=181°，以此让学生明白“平角”不是看出来的，也不是用工具测量出来的（测量工具有误差）。

学生感受到“眼见未必为实”，认为“把三角形的三个角剪下来拼凑在一起，然后通过观察得到它是一个平角”这种方法是不可靠、不严谨的。

（四）推理论证

教师结合“帕斯卡的推理”，带领学生验证“三角形的内角和是180°”，过程如下。

教师通过几何画板演示：任意一个直角三角形，作一个与其全等的直角三角形，把两个全等的直角三角形重新组合，拼成一个矩形，这个矩形的四个内角都是直角，它的内角和是360°。学生交流、反馈，得到“每一个直角三角形的内角和是180°”的结论。

接着，教师引导学生寻找一个“一般”的三角形并证明它的内角和也是180°（如图5）：任意一个锐角三角，作三角形的一条高把它分成两个直角三角形，因为直角三角形的内角和是180°，所以两个直角三角形的内角和是360°，因为有两个直角拼在一起了，所以锐角三角形的内角和是180°，∠1+∠2+∠3+∠4+∠5=180°×2=360°，∠4+∠5=90°+90°=180°，所以∠1+∠2+∠3=180°，让学生体会转化的思想和方法。

“現在我们能说每一个三角形的内角和都是180°了吗？为什么？我们只能说‘每一个锐角三角形的内角和也是180°，还需要论证‘每一个钝角三角形的内角和是180°。”教师通过设问引导学生继续探究钝角三角形的内角和。

这样的教学安排，使学生意识到数学论证需要经过全面、周密、严谨的思考，保证数学结论具有科学性。

（五）升华情感

教师向学生讲述少年帕斯卡的故事：“300多年前，法国有一位伟大的数学家、物理学家、哲学家和散文家叫帕斯卡，他在12岁的时候就发现这一规律，他还用‘推理的方法确保每一个三角形的内角和都是180°。”以此激励学生刻苦钻研。

（六）解决问题、拓展应用（略）

整个教学过程，通过情境让学生感悟到实验归纳得到的结论可能不靠谱，适度吸收部编版教材的“证明法”，即少年帕斯卡的推理进行说理论证。我们称之为“实验法+证明法”。

小学“图形与几何”教学的核心目标不是培养演绎推理能力，少年帕斯卡的推理论证也许谈不上是“演绎推理”的证明，我们采用“实验法+证明法”进行教学重在引导学生合情推理、发现规律，符合课标要求的“启蒙理性精神和演绎推理意识”。

（责编 刘小瑗）