利用Laplace变换的分布阶微分方程数值解法*

王　征，　胡长流

(1.郑州大学 西亚斯国际学院，河南 新郑 451150;2.河南大学 数学与统计学院，河南 开封 475004)

分数阶微分方程(fractional differential equations, FDE)可更好地拟合工程实践中的一些自然物理过程[1]，在工程、物理及环境问题的研究中得到应用[2-3].分布阶微分方程是分数阶微分方程的积分，其以阶次作为积分变量对分数阶微分算子进行积分运算.分布阶微分方程能够更好地描述一些动力系统，如超慢径向扩散过程、多维随机游走模型等[4].对分布阶次微分方程进行精确求解依然是一个难题.[5]提出一种求解分布阶FDE的方法，采用标准梯形规则来离散化分布阶FDE，并采用一种称为 Adams的方法来求解离散化的FDE，但其求解精度不高.本文提出一种分布阶微分方程的数值方法，使用一种隐式梯形规则对积分区间进行离散化，将分布阶FDE转化为多项式FDE，利用Laplace变换来求解多项式FDE.数值实验结果证明了提出方法的有效性.

设x∶[a,b]→R是一个正非整数，n∈N且α∈(n-1,n).α阶Riemann-Liouville分数阶积分可通过任意实数阶Cauchy方程产生，其定义如下：

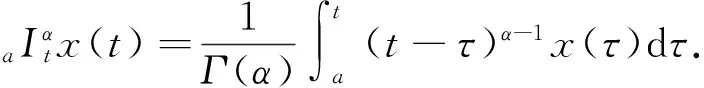
Riemann-Liouville分数阶微分和Caputo分数阶微分可以分别定义为

以上两种分数阶微分存在着一定的联系，它们的关系可以由下式表示：

分布阶FDE形式表示为

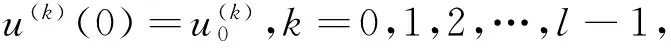
1　分布阶FDE数值方法

分布阶FDE数值方法包括两个步骤：(1)使用一种隐式梯形规则来近似分布阶FDE积分，将分布阶FDE转化为多项式FDE；(2)采用一种Laplace变换过程来求解积分区间离散化后产生的多项式FDE.

考虑一种简单的分布阶FDE形式，即α=0，表示如下：

(1)

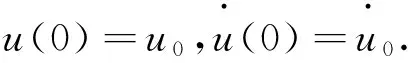
1.1　基于梯形规则近似分布阶FDE为多项式FDE

使用等间隔K的梯形规则来近似式(1)中的积分，得到多项式FDE，表示为：

(2)

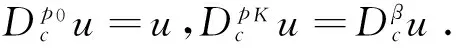
1.2　基于Laplace变换求解多项式FDE

(3)

式中q(t)为一个未知的虚拟源函数.使用Laplace变换法将式(3)中初始值问题的解转换为等效Volterra积分方程[6]:

(4)

式(4)将在时间间隔[0,T]内进行求解.将[0,T]划分为N个相等的区间Δt=h,h=T/N.在该分析中，假定q(t)恒等于每个间隔h中的平均值.因此，式(4)在t=nh时刻可写为：

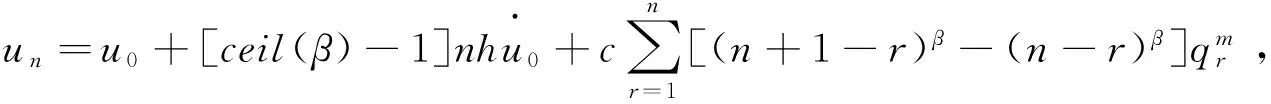
(5)

式中,q(i)(t)为另一未知源函数.通过式(3)和式(5)的Laplace变换，可以用q(t)来表示q(i)(t)：

式中,U(s)、Q(s)和Q(i)(s)分别为u(t)、q(t)和q(i)(t)的Laplace变换[7].等价替换上述方程的右端将产生：

(6)

对式(6)进行Laplace逆变换[8]，得

(7)

将时间间隔[0,T]进行相同离散化，以此近似式(7)中的积分，得到

(8)

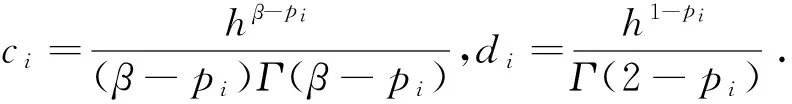
对于t=nh，式(2)表示的多项式FDE可变为：

(9)

q0是该方法的一个重要组成部分.对于n=0，式(9)变为

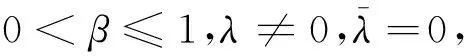
至此，完成了对式(2)所示的多项式FDE的求解，进而实现了对式(1)所示的分布阶FDE的求解.

2　数值实例

为了验证提出方法的准确性和收敛性，利用MATLAB编程进行数值实验，在PC机上进行计算.

实例求解一个分布式FDE方程，形式如下：

表1　不同K值和h值下u(0.5)的误差

hK248160.10.045460.018320.005980.000480.050.040040.016090.005740.000370.0250.038010.015940.005550.000360.01250.036460.015760.005010.000270.006250.035660.014470.004920.000230.0031250.034280.014270.004680.000190.00156250.034110.013670.004550.00017

将本文方法与[5]方法进行比较，[5]方法也采用了标准梯形规则来离散化分布阶FDE.不同于本文方法，[5]方法采用了Adams方法来求解离散化后的多项式FDE.图1为当h=0.001和K=16时，在不同t下的误差u(t)-uex(t)，本文方法与[5]方法误差的比较.如图1所示，随着t的增加，本文方法的误差增大，但整体上保持为一个很小的值，且在所有情况下，本文方法的误差都小于[5]方法.

[1]汪亚运, 陈得良, 彭旭龙,等. 微分求积法在弹性压应力波下直梁的动力压曲稳定分析中的应用[J]. 湘潭大学自然科学学报, 2016, 38(3): 30-34.

[2]SHI W J,ZHANG C J. Generalized polynomial chaos for nonlinear random fredholm equations [J]. Acta Mathematicae Applicatae Sinica(English Series), 2016, 32(3): 685-700.

[3]张滑, 刘春凤. 分数阶R-L微分方程初值问题解的存在唯一性[J]. 数学的实践与认识, 2016, 46(3): 267-272.

[4]KHARAZMI E, ZAYERNOURI M, KARNIADAKIS G E. Petrov-galerkin and spectral collocation methods for distributed order differential equations [J]. Mathematics, 2016, 24(3): 1-31.

[5]DIETHELM K, FORD N J. Numerical analysis for distributed-order differential equations [J]. Journal of Computational & Applied Mathematics, 2009, 225(1): 96-104.

[6]洪志敏, 闫在在. Volterra积分方程的蒙特卡罗数值求解方法[J]. 数学杂志, 2016, 36(2): 425-436.

[7]ATONUJE. Issues in the influence of ito-type noise on the oscillation of solutions of delay differential fredholm equations[J].数学和系统科学:英文版, 2015, 26(11): 480-487.

[8]HUANG Q, XIE H, BRUNNER H. Super convergence of discontinuous galerkin solutions for delay differential equations of fredholm type.[J].计算数学:英文版, 2016, 33(2): 186-199.