旋转桌面上滚动硬币系统建模与基于微分平坦的轨迹生成*

李顺杰,　马欣键

(南京信息工程大学 数学与统计学院，江苏 南京 211800)

作为一个经典非完整约束系统，滚动硬币系统的运动学模型可描述为一个无漂移双输入非线性系统[1].近年来，Kai在文献[2]中首次研究了匀速旋转桌面上滚动硬币系统，给出了该系统满足的仿射非完整约束条件，建立了其运动学模型，并根据系统模型研究了该系统的轨迹生成问题.作者通过研究发现，Kai建立的匀速旋转桌面上滚动硬币系统的运动学模型是错误的，原因在于他提出的非完整约束条件混淆了硬币的绝对运动和相对运动.本文分析并修正了匀速旋转桌面上滚动硬币系统的非完整约束条件，从而推导出系统正确的运动学模型.此外，分析了该系统的微分平坦性，证明了匀速旋转桌面上滚动硬币系统是微分平坦的，并给出了系统的微分平坦输出.最后，利用微分平坦系统的性质研究了该系统点到点的可行轨迹生成问题，并利用MATLAB仿真验证了结果的有效性.本文结果为今后继续研究可任意运动平台上的移动机器人系统的轨迹规划及轨迹跟踪问题奠定了理论基础.

1　旋转桌面上滚动硬币系统模型

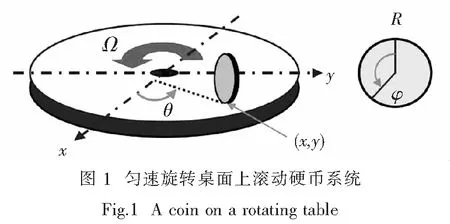
考虑匀速旋转桌面上滚动硬币系统，如图1所示，其中，R>0为硬币的半径，Ω为桌面旋转角速度且是一个常数.用q=(x,y,θ,φ)表示系统的广义坐标，其中(x,y)表示硬币与桌面接触点的坐标，θ表示硬币运动方向相对x轴的偏角，φ为硬币运动时相对于竖直方向的偏角.

1.1　Kai模型分析

Kai指出匀速旋转桌面上滚动硬币系统满足以下仿射非完整约束条件[2]：

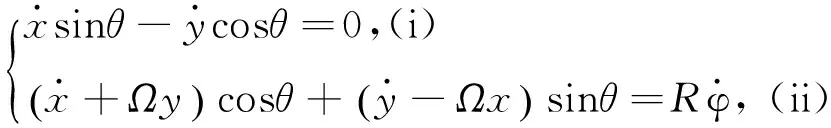
(1)

并根据约束条件(1)得到系统运动学模型：

(2)

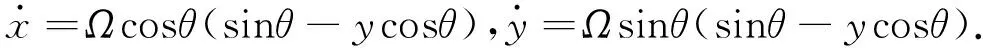
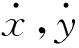
1.2　旋转桌面上滚动硬币系统模型

在匀速旋转桌面上研究硬币的运动，显然需要考虑到桌面旋转对硬币位置变化的影响，因此，保留非完整约束条件(1)-(ii)的同时，需要修正非完整约束条件(1)-(i).通过上述分析可知，正确的非完整约束条件(1)-(i)为

显然上述约束条件可由仿射非完整约束(1)-(ii)得到，即它蕴含在仿射非完整约束(1)-(ii)中.因此，匀速旋转桌面上滚动硬币系统实际上只有一个仿射非完整约束(1)-(ii)，即

(3)

直接计算可得正确的匀速旋转桌面上滚动硬币系统的运动学模型如下：

(4)

同时，系统Σc的平衡点为{q=(x,y,θ,φ):x=y=0}.

2　系统微分平坦性分析

2.1　微分平坦

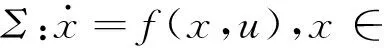
基于微分平坦系统良好的结构特性，满足微分平坦的非线性系统的轨迹规划和轨迹跟踪等问题都能够得到非常直接的解决方案，因此在自动控制领域逐渐得到了广泛的应用[8-11].

2.2　匀速旋转桌面上滚动硬币系统的微分平坦性

首先简要介绍几个微分几何概念，详细内容可参考文献[1,5].考虑m维分布Δ=span{g1,…,gm}，定义分布序列Δ0=Δ,Δi+1=Δi+[Δi,Δi]，i≥0.设向量场c∈Δ，如果[c,Δ]⊂Δ，则称c为分布Δ的不变特征向量场.Δ的所有不变特征向量场构成的分布C称作Δ的不变特征子分布，即C=span{c∈Δ:[c，Δ]⊂Δ}.

世人皆好责人而非责己。在“异常人”的眼中：别人都是豆腐渣，唯有自己是一朵花。“正常人”则不然。他宽以待人，严于律己。金无足赤，人无完人。“正常人”敢于解剖自己，善于反省自己。他做人的信条是：只有敢于袒露自己心声的人，才值得信赖，也才有资格评判他人！

下面的定理为[6]中主要结论的特殊形式，详细证明可参考[6].

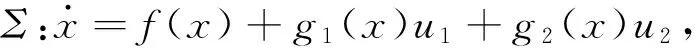
其中x∈X⊂R4，f,g1,g2均是C向量场.设G为向量场g1,g2构成的分布，即G=span{g1,g2}，且C1为分布G1的不变特征子分布.如果Σ满足[f,C1]⊂G1且rankGi=i+2, 0≤i≤2，则系统Σ是x-微分平坦的，同时，双输入无漂移非线性系统的任意x-平坦输出都是Σ的x-平坦输出.

定理2匀速旋转桌面上滚动硬币系统Σc是x-微分平坦的.

证明只需验证Σc满足条件[f,C1]⊂G1与rankGi=i+2, 0≤i≤2.根据系统模型得

f=(-Ωy，Ωx，0，0)T,g1=(0，0，1，0)T,g2=(Rcosθ，Rsinθ，0，1)T.

(5)

直接计算可得

g3=[g1,g2]=(-Rsinθ，Rcosθ，0，0)T,g4=[g1,g3]=(-Rcosθ，-Rsinθ，0，0)T.

因为G1=span{g1,g2,g3}，G2=span{g1,g2,g3,g4}，显然rankG1=3,rankG2=4，即条件rankGi=i+2,0≤i≤2满足.容易验证分布G1的不变特征子分布C1=span{g2}，直接计算可得[f,g2]=-Ωg3∈G1，即条件[f,C1]⊂G1满足.因此，由定理1，匀速旋转桌面上滚动硬币系统Σc是x-微分平坦的.此外，原系统对应的无漂移系统

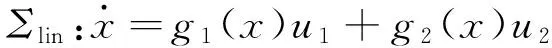
的任意x-平坦输出都是Σc的x-平坦输出，其中g1,g2由(5)给出.注意到，无漂移非线性系统Σlin实际上就是经典滚动硬币系统的运动学模型[1,7]，根据[7]的结论，

h=(h1,h2)=(θ,Rφ-xcosθ-ysinθ)

(6)

是Σlin的一组x-平坦输出，因此，可以选择(6)作为系统Σc的一组x-平坦输出.容易验证系统Σc的状态变量x,y,θ,φ以及控制输入u1,u2均可表示为h1,h2及其有限阶导数的函数：

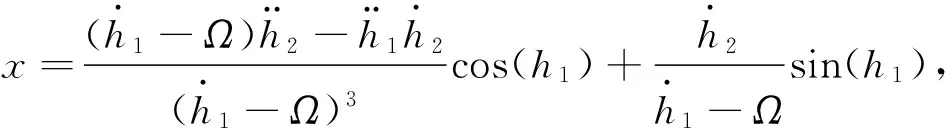
(7)

3　基于微分平坦的轨迹生成

本节将研究匀速旋转桌面上滚动硬币系统Σc在给定初始状态和终端状态时的点到点轨迹生成问题.一般来说，非线性系统点到点轨迹生成问题是比较困难的，尤其对于非完整约束系统，因为并不是所有轨迹都是可行的.但是，如果系统是微分平坦的，初始状态和终端状态可以转化为系统平坦输出及其有限阶导数的初始条件和终端条件，然后在平坦输出空间中选择满足初始和终端条件的轨迹，最后利用逆映射得到原系统的可行轨迹[3].在平坦输出空间中选择可行轨迹有多种方法，为方便起见，本文将选择基于多项式的轨迹生成方法.

首先建立系统Σc的状态空间与平坦输出空间的微分同胚映射.通过(7)可以看出，在将系统的状态变量x,y,θ,φ以及控制输入u1,u2表示为h1,h2及其有限阶导数的函数时，需要用到平坦输出h1,h2的三阶导数.直接计算可得h1,h2及其各阶导数用系统状态、输入及其导数表示如下：

(8)

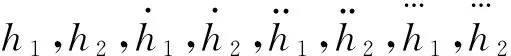
4　仿真结果

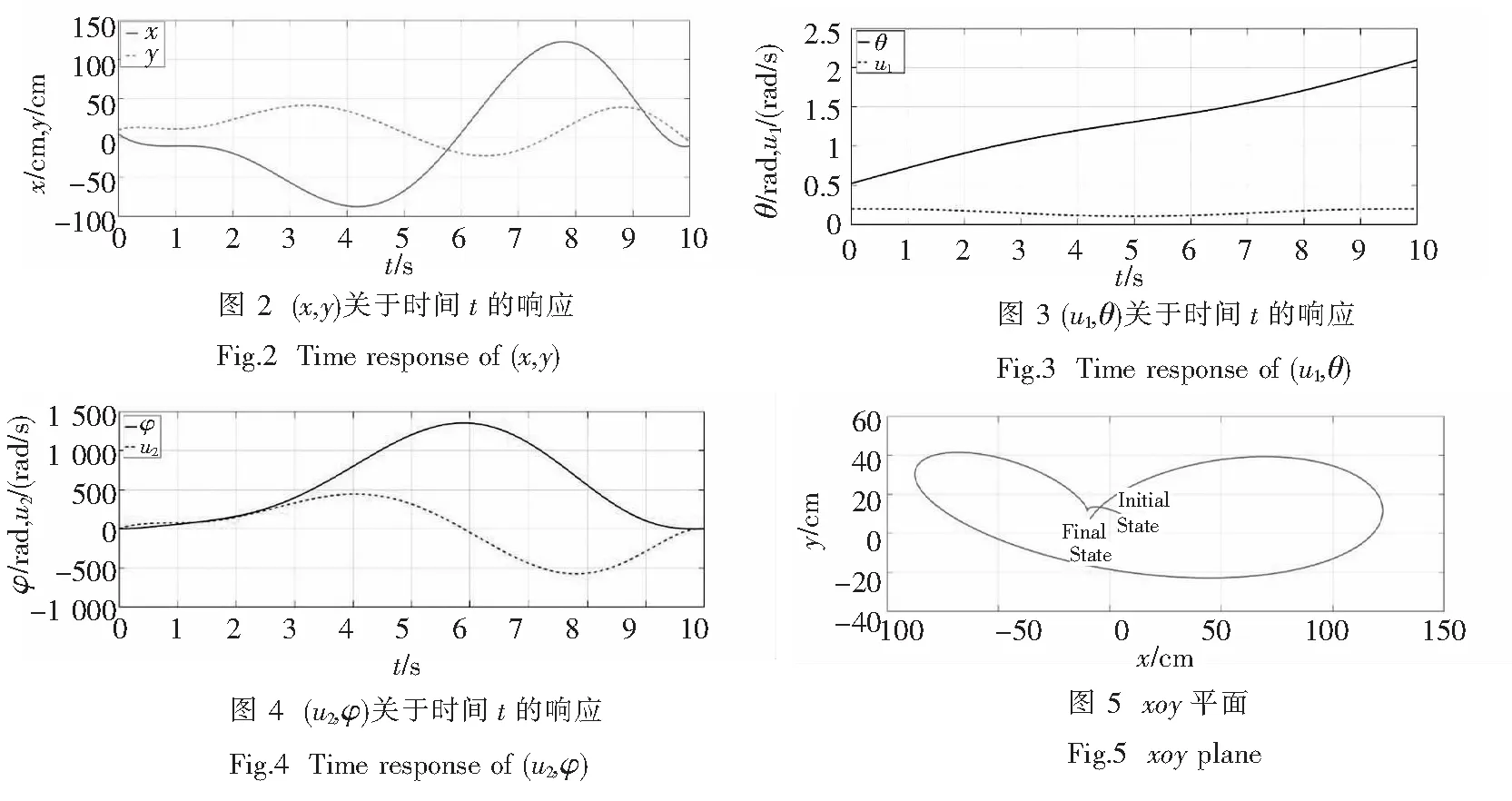
给定系统参数为R=1 cm,Ω=5 rad/s,系统初始状态为：x(0)=5 cm,y(0)=10 cm，θ(0)=π/6 rad,φ(0)=π/12 rad；系统终端状态为：x(tf)=-10 cm，y(tf)=-5 cm，θ(tf)=2π/3 rad,φ(tf)=-π/4 rad，设终端时刻为t=tf=10 s.

利用MATLAB得到仿真结果如图2～图5所示.

5　结　论

本文研究了匀速旋转桌面上滚动硬币系统的运动学建模以及基于微分平坦的点到点轨迹生成问题.首先，指出了Kai在建立该系统仿射非完整约束及运动学模型时的错误并加以修正，从而给出了正确的仿射非完整约束条件及其运动学模型.其次，证明了该系统是x-微分平坦的，且其对应的无漂移非线性系统的所有平坦输出都可作为该系统的平坦输出.最后，利用微分平坦系统的性质，研究了该系统点到点的轨迹生成问题，并利用MATLAB给出了仿真结果.

[1]BLOCH A M. Nonholonomic mechanics and control [M]. New York:Springer-Verlag, 2007.

[2]KAI T. Extended chained forms and their application to nonholonomic kinematic systems with affine constraints:control of a coin on a rotating table [C]. Proceedings of the IEEE Conference on Decision & Control, 2006:6104-6109.

[3]FLIESS M,LEVINE J,MARTIN P, et al. Flatness and defect of nonlinear systems: introductory theory and examples [J]. International Journal of Control, 1995, 61(6): 1327-1361.

[4]FLIESS M,LÉVINE J,MARTIN P, et al. A Lie-Backlund approach to equivalence and flatness of nonlinear systems [J]. IEEE Transactions on Automatic Control, 1999, 44(5):922-937.

[5]AlbertoIsidori. Nonlinear control systems [M].London:Springer-Verlag，1995.

[6]LI S J,NICOLAU F,RESPONDEK W. Multi-input control-affine systems static feedback equivalent to a triangular form and their flatness [J]. International Journal of Control，2016， 89(1):1-24.

[7]LI S J,RESPONDEK W. Describing and calculating flat outputs of two-input driftless control systems [C]. Proc of IFAC Symp NOLCOS'2010, Bologna.2010: 689-694.

[8]ZHUANG Y F,MA G F,LI C J,et al. Time-optimal trajectory planning for underactuated rigid spacecraft using differential flatness [J]. Journal of Astronautics, 2011， 32(8): 1753-1761.

[9]MARKUS E D，AGEE J T,JIMOH A A. Flat control of industrial robotic manipulators[J]. Robotics & Autonomous Systems，2016, 87:226-236.

[10]孙宁，方勇纯，钱彧哲. 带有状态约束的双摆效应吊车轨迹规划[J]. 控制理论与应用，2014, 31(7): 974-980.

[11]蔡伟伟，杨乐平, 刘新建，等. 基于微分平坦的高超声速滑翔飞行器轨迹规划[J]. 国防科技大学学报, 2014, 36(2): 61-67.