基于改进蝙蝠算法的多传感器多目标分配

张士磊，　张　朋，　熊志刚

(1.河南工学院自动控制系,河南 新乡　453003；　2.中原工学院电子信息学院,郑州　451191; 3.空军工程大学防空反导学院，西安　710051)

0　引言

在防空作战体系中，单个传感器往往不能完成对目标的检测、识别和跟踪任务，多数情况下需要多个传感器同时针对一个目标进行探测，然后对多个传感器探测到的数据进行信息融合。传感器管理包括多传感器交叉提示和传感器控制两个方面，是信息融合的反馈环节，主要解决多个传感器探测多个目标时的资源调度问题。一方面由于每个传感器的探测能力有限，多个目标来袭时，每一个传感器不能同时对每个目标

进行探测，这就对传感器合理分配提出了需求;再者，如果每一个传感器同时对每个目标都进行探测，容易造成信息冗余和资源浪费。另一方面，由于对每个目标的探测任务(检测、识别、跟踪)不同，也必须解决传感器针对不同传感器不同任务的资源协调问题，在确保完成对目标的探测任务的情况下达到传感器系统最优性能，同时使传感器资源消耗最少。

多传感器多目标分配属于组合爆炸NP问题，针对此问题，已经有许多学者作了探讨。在国外，JEFFREY N等将优化思想引入到解决传感器分配问题当中，得到了传感器分配方案，但该算法的求解速度较慢，求解质量较低；NASH J M等利用线性规划的方法对传感器资源进行分配，得到了较为理想的可行解，但该算法的复杂度较高[1]；CASTANON D A等采用动态规划的方法有效解决了传感器分配问题[2]；KASTELLA K等提出了一种基于信息熵和分辨力增益的传感器管理方法，得到了较为理想的多传感器多目标分配方案，但算法稳定性较差[3]。

随着智能算法的发展，学者们将群智能算法引入到解决多传感器多目标分配问题。在国内，朱卫宵等将遗传算法用于解决多传感器多目标分配问题，有效地得到了分配方案，该算法全局搜索能力较强[4]；黄树彩等提出了一种基于蚁群算法的多传感器多目标分配算法，该算法具有较快的收敛性和较高的精度，但易陷入局部最优[5]；樊浩等引入并改进了粒子群算法用于传感器交叉提示多目标探测动态联盟模型求解，并证明了该算法的有效性[6]；田德伟等提出了基于萤火虫算法的雷达目标分配方法，并证明该算法具有收敛速度快、求解结果稳定的优点[7]；杨啸天等将遗传算法和粒子群算法结合起来，建立了基于遗传粒子群算法的多传感器多目标分配模型，有效实现了传感器资源对目标的分配，该算法性能较以往算法大大提高[8]。

通过研究可以看出，寻找一种简单易行的有效求解算法，并提高算法的收敛速度和稳定性，有效跳出局部最优，一直是学者探讨的重点。对此，本文引入并改进蝙蝠算法解决此类问题，并通过仿真实验证明了本文算法的有效性和先进性。

1　传感器-目标配对模型

设传感器网络有m个传感器{s1,s2,…,sm}，来袭目标有n个{t1,t2,…,tn}，需将m个传感器分配给n个目标进行探测。

设分配方案用m×n阶矩阵X表示，其中，xij为X的第i行第j列元素,表示传感器si对目标tj的监测状态,即

(1)

传感器对目标的探测能力用m×n阶矩阵P表示，其中，pij为P的第i行第j列元素,表示传感器si对目标tj的探测概率。

目标优先级用1×n阶矩阵F1表示，其中，fi为目标tj的优先级，其值大小表示该目标对我方防御系统的威胁程度，本文中有

(2)

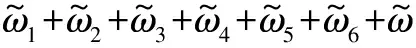
(3)

传感器重要级用m×1阶矩阵F2表示，其中，ci为传感器si的重要级，其值大小表示该传感器在我方传感器网络中担负战备任务的重要程度，本文中有

ci=βi 1η1+βi 2η2+βi 3η3+βi 4η4+βi 5η5

(4)

η1+η2+η3+η4+η5=1

(5)

式中：ηk表示影响传感器重要级的第k个因素所占权重；βi 1为传感器属性；βi 2为传感器部署位置；βi 3为传感器探测区域；βi 4为传感器类型；βi 5为传感器抗干扰能力。

目标函数如下所述。

1) 传感器网络对目标的总探测概率最大，同时考虑目标优先级，有

(6)

式中，pj为传感器网络对目标tj的探测概率。pj的计算方法为

pj=1-(1-x1j×p1j)(1-x2j×p2j)…(1-xmj×pmj)。

(7)

2) 传感器网络消耗的传感器资源最少，有

(8)

约束条件有以下2个。

1) 传感器实际探测的目标个数小于其探测能力，有

(9)

式中，Mi为传感器si可同时探测的最大目标数。

2) 应保证有传感器对目标tj进行探测，有

(10)

评价多传感器-多目标分配方案X的好坏，需要建立一定的评价指标，即适应度函数G(X)，其计算方法为

(11)

2　改进蝙蝠算法设计

2.1　基本蝙蝠算法

蝙蝠算法(Bat Algorithm，BA)由YANG X S于2010年提出[10]，其算法来源于自然环境中蝙蝠依靠超声波搜索和捕食的行为，具有模型简单、计算方便、参数设置较少等优点，其基本蝙蝠算法的寻优机制如下所述。

1) 算法初始化。t=0时刻，将每个蝙蝠看作一个可行解，给定种群蝙蝠个数、蝙蝠位置、速度、脉冲速度、脉冲频率、脉冲响度，根据适应度函数对每个蝙蝠作出评价，确定最优蝙蝠位置。

2) 更新蝙蝠速度和位置。t时刻，对蝙蝠的速度和位置进行更新，即

(12)

(13)

ha=hmin+(hmax-hmin)×R

(14)

3) 生成随机数R1。若R1>ra，通过随机游走的方法使蝙蝠进行局部搜索，生成新解，其生成方法为

xnew=xold+εAt。

(15)

4) 生成随机数R2。若R2

(16)

(17)

5) 寻找更新后最佳适应度蝙蝠，并记录。

6) 判断是否达到最大迭代次数，或者达到搜索精度ε1，若达到，则结束迭代，将最优蝙蝠位置及其所对应的适应度输出；否则，返回步骤3)。

通过上述基本蝙蝠算法中蝙蝠的全局位置更新和局部位置更新方法可知，该算法一味向群体最优蝙蝠位置收敛，随着算法迭代次数的增加，在迭代后期，群体的个体差异性越来越小，种群多样性越来越低，甚至最终趋于0，一方面会导致群体进化能力降低，另一方面容易造成早熟，从而陷入局部最优。虽然式(16)与式(17)对算法早熟起到一定的抑制作用，但其效果并不明显，对此，在基本蝙蝠算法的基础上进行改进，提出改进蝙蝠算法。

2.2　改进蝙蝠算法

针对蝙蝠算法易发生早熟、陷入局部最优等缺点，主要进行如下改进。

2.2.1K-均值算法初始化

初始化生成蝙蝠群体，该群体应均匀分布在求解空间当中，以此才能对全局进行更好搜索。而在基本蝙蝠算法中，初始化过程中蝙蝠群体是随机生成的，可能存在蝙蝠局部“扎堆”的现象，使蝙蝠群体在一开始就失去全局搜索能力，引起局部最优，对此，设初始化群体中蝙蝠数量为N，提出基于K-均值的种群初始化方法，其步骤为：

1) 随机生成N只蝙蝠作为聚类中心，共有N个聚类簇；

2) 随机生成N1只蝙蝠，将每只蝙蝠划分到离其最近的聚类簇当中；

3) 再次计算N个聚类簇的聚类中心；

4) 重复步骤2)和3)，直至前后两次聚类中心的变化区域小于给定的阈值Δ；

5) 输出最后的N个聚类中心作为初始化群体中的N只蝙蝠个体。

2.2.2自适应步长

在蝙蝠运动过程中，其移动速度过慢，会降低算法收敛速度，而移动太快，则可能会“越过”最优值[11]。在算法迭代开始时，蝙蝠移动速度应较大，从而提高向最优解收敛的速度，而算法迭代后期，蝙蝠移动速度应较小，从而在最优解周围能够充分搜索，避免“错过”最优解，因此，提出基于自适应步长的蝙蝠速度更新方法，每次迭代过程中，更新蝙蝠速度，即

(18)

(19)

式中：smin为最小步长，取smin=0.01；Tmax为最大迭代次数；t为当前迭代次数；K为系数，取K=10。

由式(18)、式(19)可以看出，算法初期步长较大，以此提高收敛速度；算法后期步长较小，以此精细搜索。

2.2.3向反方向搜索及变异操作

由于在迭代过程中，所有蝙蝠均向适应度高的蝙蝠位置移动，种群多样性大大降低，对此，每次迭代过程中，对所有蝙蝠按照适应度从高到低的顺序排序，挑选适应度排名最后的N2只蝙蝠，产生值为0～1的随机数R3。若R3>0.5，其位置按照

(20)

更新，使种群按照两个方向进化，从而提高种群多样性。若0

(21)

更新。式中：R为0～1的随机数；xmin为蝙蝠最大位置；xmax为蝙蝠最小位置。

2.3　改进蝙蝠算法步骤

通过2.2节所述，改进蝙蝠算法步骤为：

1) 算法初始化，t=0时刻，将给定各参数，按照K-均值算法生成在求解空间内均匀分布的N只蝙蝠；

2) 计算每只蝙蝠的适应度，并排序；

3) 按照式(13)、式(14)、式(18)～(21)更新蝙蝠速度和位置；

4) 生成随机数R1，若R1>ra，通过随机游走的方法使蝙蝠进行局部搜索，生成新解，新解生成方法如式(15)所示；

5) 生成随机数R2，若R2

6) 寻找更新后最佳适应度蝙蝠，并记录；

7) 判断是否达到最大迭代次数，或者达到搜索精度ε1，若达到，则结束迭代，将最优蝙蝠位置及其所对应的适应度输出,否则，返回步骤2)。

3　仿真验证

传感器网络中共有10个传感器，来袭目标共有6个，各传感器对目标的探测能力见表1，其中各传感器重要级和目标优先级均采用归一化表示。

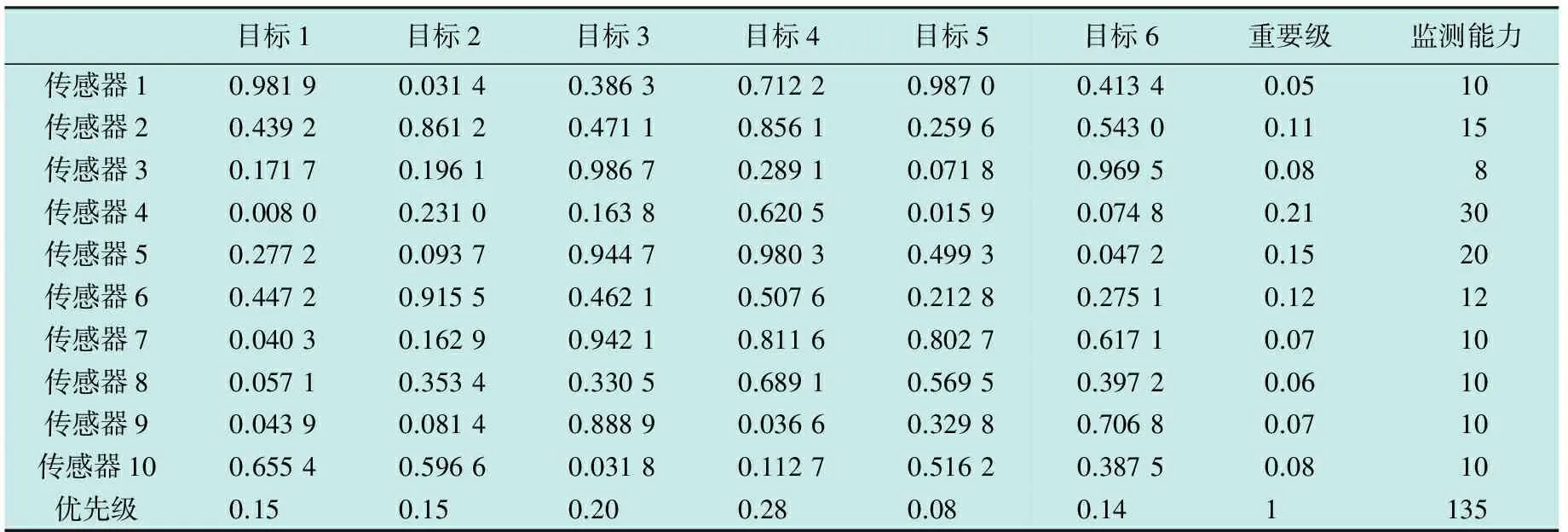
表1　传感器对目标的探测能力

在仿真过程中，参数设置分别为：蝙蝠数量N=30，N2=6，最大迭代次数为Tmax=2000，蝙蝠最大频率hmax=2.0，初始响度为区间[0,2]内的随机数，初始脉冲取[0,0.05]内的随机数，α=β=0.9，蝙蝠最大速度vmax=0.5(无量纲值)。

3.1　蝙蝠算法改进前后对比

分别采用基本蝙蝠算法、改进蝙蝠算法计算多传感器-多目标分配方案，经过100次蒙特卡罗实验，其迭代过程对比如图1所示，最终分配结果如表2所示。

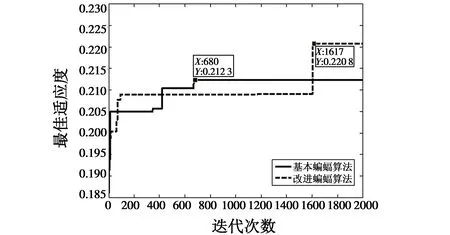
图1　两种算法迭代路线对比Fig.1　The contrast of iterative courses of two algorithms

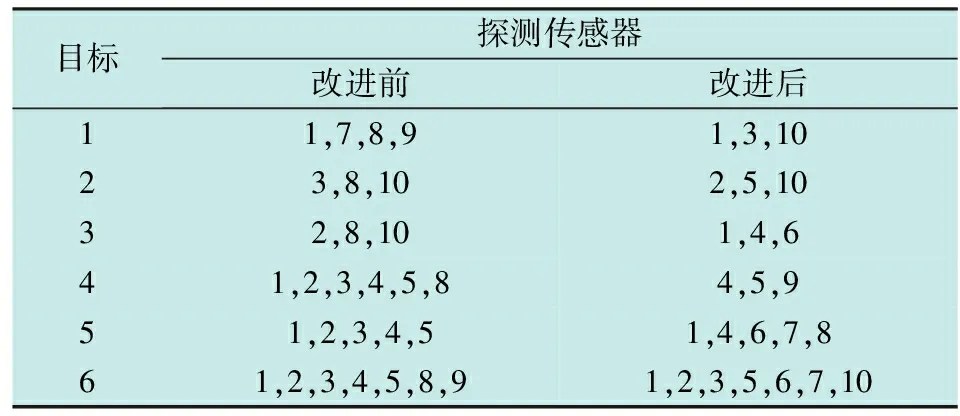
目标探测传感器改进前改进后11，7，8，91，3，1023，8，102，5，1032，8，101，4，641，2，3，4，5，84，5，951，2，3，4，51，4，6，7，861，2，3，4，5，8，91，2，3，5，6，7，10

由图1可知，改进蝙蝠算法和基本蝙蝠算法都能有效解决多传感器-多目标分配问题。

基本蝙蝠算法计算时间为3.8 s，改进蝙蝠算法计算时间为2.1 s，基本蝙蝠算法在改进后，计算速度明显提高。基本蝙蝠算法在680次计算后趋于稳定，方案适应度不再提高，计算得到的最优方案适应度值为0.212 3，而改进蝙蝠算法在计算93～1617次之间，方案适应度稳定，而当计算到1617次时，方案适应度又有所提高，计算得到的最优方案适应度值为0.220 8，说明其能够跳出局部最优，基本蝙蝠算法在改进后，其寻优能力有所增强。

3.2　蝙蝠算法与其他智能算法对比

分别采用本文改进蝙蝠算法与文献[12]中的粒子群算法、文献[13]中的蜂群算法、文献[14]中的狼群算法求解多传感器-多目标分配方案，经过100次蒙特卡罗实验，其迭代过程对比如图2所示。

图2　4种算法迭代路线对比Fig.2　The contrast of iterative courses of four algorithms

本文改进蝙蝠算法计算时间为1.9 s，粒子群算法计算时间为4.1 s，蜂群算法为3.2 s，狼群算法为2.5 s，本文算法求解速度最快。

由图2可知，本文所提出的改进蝙蝠算法，在求解多传感器-多目标分配方案过程中，无论求解速度，还是求解质量，均优于其他3种算法。

4　结论

针对多目标多传感器分配中的NP爆炸问题，本文引入蝙蝠算法进行求解，并通过K-均值算法初始化、速度更新采用自适应步长、向反方向搜索及变异操作等3项措施对基本蝙蝠算法易陷入局部最优、存在早熟现象等问题进行了改进，得到改进的蝙蝠算法。仿真实验表明蝙蝠算法在改进后，不仅其计算速度和寻优能力相对于基本蝙蝠算法大大提高，而且其求解速度和求解质量也均优于粒子群算法、蜂群算法、狼群算法等其他算法。因而，本文算法更适用于多传感器多目标分配问题求解，其求解质量更高。

[1]NASH J M.Optimal allocation of tracking resources[C]//1977 IEEE Confererce on Decision and Control,1977:1177-1180.

[2]CASTANON D A.Approximate dynamic programming for sensor management[C]//Proceedings of the 36th IEEE Conference on Decision and Control,1997:1202-1207.

[3]KASTELLA K.Discrimination gain to optimize detection and classification[J].IEEE Transactions on Systems, Man,and Cybernetics,Part-A:System and Humans,1997, 27(1):112-116.

[4]朱卫宵，祝前旺，陈康.一种基于遗传算法的多传感器多目标分配方法[J].电子信息对抗技术，2015,30(3)：30-34.

[5]黄树彩，李为民，李威.多传感器管理的目标分配问题蚁群算法研究[J].空军工程大学学报:自然科学版,2005,6(2)：28-31.

[6]樊浩,黄树彩，高美凤，等.多传感器交叉提示多目标探测动态联盟技术研究[J].宇航学报，2011,32(11)：2380-2386.

[7]田德伟，何广军，尤晓亮，等.基于萤火虫算法的雷达目标分配方法[J].探测与控制学报，2015,37(2)：62-65.

[8]杨啸天，冯金富，冯媛，等.基于遗传粒子群的多传感器目标分配算法[J].电光与控制，2011,18(3)：5-8.

[9]罗文涛，许蕴山，肖冰松，等.预警探测中的多传感器多目标匹配[J].电光与控制，2014,21(11)：28-33.

[10]YANG X S.A new metaheuristic bat-inspired algorithm[J].Computer Knowledge and Technology,2010,284:65-74.

[11]杜继永，张凤鸣，李建文，等.一种具有初始化功能的自适应惯性权重粒子群算法[J].信息与控制,2012, 41(2):165-169.

[12]杨啸天，冯金富，冯媛，等.基于遗传粒子群的多传感器目标分配算法[J].电光与控制，2011,18(3)：5-8.

[13]易正俊，韩晓晶.增强寻优能力的改进人工蜂群算法[J].数据采集与处理，2013,18(6):761-769.

[14]吴虎胜，张凤鸣，吴庐山.一种新的群体智能算法—狼群算法[J].系统工程与电子技术,2013,35(11):2430-2438.